TIME, SPEED AND DISTANCE - Aptitude

Chapter 12: TIME, SPEED AND DISTANCE

Formulae

Speed = Distance / Time
Distance = Speed * Time
Time = Distance / Speed
km / hr convert to m/s by multiplying by 5/18

Direct proportionality between time and distance (when the speed is constant) time µ distance

A car moves for 2 hours at a speed of 25 kmph and another car moves for 3 hours at the same speed. Find the ratio of distances covered by the two cars.

Since, the speed is constant, we can directly conclude that time µ distance.

Hence \( \frac{t_A}{t_B} = \frac{d_A}{d_B} \)

Since, the times of travel are 2 and 3 hours respectively, the ratio of distances covered is also 2/3

Direct Proportionality between speed and distance (when the time is constant) speed µ distance

A body travels at S1 kmph for the first 2 hours and then travels at S2 kmph for the next two hours. Here two motions of one body are being described and between these two motions the time is constant hence speed will be proportional to the distance travelled

Two cars start simultaneously from A and B respectively towards each other with speeds of S1 kmph and S2 kmph. They meet at a point C…. Here again, the speed is directly proportional to the distance since two motions are described where the time of both the motions is the same, that is, it is evident here that the first and the second car travel for the same time.

In such a case the following ratios will be valid:

\( \frac{S_1}{S_2} = \frac{D_1}{D_2} \)

Q. A car travels at 30 km/h for the first 2 hours of a journey and then travels at 40 km/h for the next 2 hours of the journey. Find the ratio of the distances travelled at the two speeds.

Since time is constant between the two motions described, we can use the proportionality between speed and distance

\( \frac{S_1}{S_2} = \frac{D_1}{D_2} \)

= 3/4

Q. Two cars leave simultaneously from points A and B on a straight line towards each other. The distance between A and B is 100 km. They meet at a point 40 km from A. Find the ratio of their speeds

Since time is the same for both the motions described, we have ratio of speed = ratio of distance.

S_A / S_B = 40/60 = 2/3

Q. Two cars move simultaneously from points A and B owards each other. The speeds of the two cars are 20 m/s and 25 m/s respectively. Find the meeting point if d(AB) = 900 km

For the bodies to meet, the time of travel is constant (since the two cars have moved simultaneously).

Hence, speed ratio = distance ratio

4/5 = distance ratio

Hence, the meeting point will be 400 km from A and 500 km from B

Inverse proportionality between speed and time (when the distance is constant)

A body travels at S1 kmph for the first half of he journey and then travels at S2 kmph for the second half of the journey. Here two motions of one body are being described and between these two motions the distance travelled is constant. Hence he speed will be inversely proportional to the time travelled for.

Two cars start simultaneously from A and B respectively towards each other. They meet at a point C and reach their respective destinations B and A in t1 and t2 hours respectively... Here again, the speed is inversely proportional to the time since two motions are described where the distance of both the motions is the same, that is, it is evident here that the first and the second car travel for the distance, viz., AB.

In such a case, the following ratio will be valid

\( \frac{S_1}{S_2} = \frac{t_2}{t_1} \) or \( S_1*t_1 = S_2*t_2 = S_3*t_3 = K \)

Since Distance = speed * time, When one of either speed or time is changed, the other quantity is also changed to maintain the same distance.

Speed is increased by %	Time is reduced by %
10	9.09
20	16.66
25	20
33.33	25
50	33.33
60	37.5
75	42.85
100	50

Q. A train meets with an accident and moves at 3/4 its original speed. Due to this, it is 20 minutes late. Find the original time for the journey beyond the point of accident.

Solving mathematically S₁ /S₂ = t₂ /(t₂ + 32)

5/7.5 = t₂/(t₂ + 32)

5t_{2 + 160 = 7.5 t₂}

t₂ = 160/2.5 = 64 minutes

Hence, the distance is given by 7.5 × 64/60 = 8 km

Q. A train meets with an accident and moves at 3/4 its original speed. Due to this, it is 20 minutes late. Find the original time for the journey beyond the point of acciden

we get that a 25% reduction in speed leads to a 33.33% increase in time.

But, 33.33% increase in time is equal to 20 minutes increase in time.

Hence, total time (original) = 60 minutes

Problems on Trains and Poles

Time taken by a train of length X metres to pass a pole or a standing man or a signal post is equal to the time taken by the train to cover X metres.

Time taken by a train of length X metres to pass an object of width Y meters is equal to the time taken by the train to cover X + Y metres.

Suppose two trains or two bodies are moving in the same direction at A m / s and B m/s, where A > B, then their relatives speed = (A - B) m / s.

Suppose two trains or two bodies are moving in opposite directions at A m / s and B m/s, then their relative speed is = (A + B) m/s.

If two trains of length a metres and b metres are moving in opposite directions at u m / s and v m/s, then time taken by the trains to cross each other = (a + b)/(u+v) sec.

If two trains of length a metres and b metres are moving in the same direction at u m / s and v m / s, ; then the time taken by the faster train to cross the slower train = (a+b)/(u-v) sec.

If two trains (or bodies) start at the same time from points A and B towards each other and after crossing they take a and b sec in reaching B and A respectively, then (A's speed) : (B’s speed) = \( b^{1/2} : a^{1/2} \)

Boats and Streams

If speed of boat in still water is X km/hr and speed of stream is Y km/hr then speed of boat downstream is (X+Y) km/hr.

If speed of boat in still water is X km/hr and speed of stream is Y km/hr then speed of boat in going upstream [against flow] is (X- Y) km/hr.

If speed of boat downstream is a km/hr and speed of boat upstream is b km/hr.

Then speed of boat in still water = 1/2(a+b)

Then speed of stream = 1/2(a-b)

Q. A train crosses a pole in 8 seconds. If the length of the train is 200 metres, find the speed of the train.

In this case, it is evident that the situation is one of the train crossing a stationary object without length.

Thus, S_T = 200/8 = 25 m/s so 25 × 18/5 = 90 kmph.

Q. A train crosses a man travelling in another train in he opposite direction in 8 seconds. However, the train requires 25 seconds to cross the same man if the trains are travelling in the same direction. If the length of the first train is 200 metres and that of the train in which the man is sitting is 160 metres, find the speed of the first train.

Here, the student should understand that the situation is one of the train crossing a moving object without length. Thus the length of the man’s train is useless or redundant data.

(Speed of first train + Speed of second train) * time taken to cross when moving in opposite direction = length of first train

(Speed of first train - Speed of second train) * time taken to cross when moving in same direction = length of first train

Equating RHS we finally get Speed of first train as 59.4 kmph / 16.5 mps

Acceleration is defined as the rate of change of speed. Acceleration can be positive (speed increases) or negative (speed decreases also known as deceleration)

The unit of acceleration is speed per unit time (e.g. m/s²)

For instance, if a body has an initial speed of 5 m/s and a deceleration of 0.1 m/s² it will take 50 seconds to come to rest

Final speed = Initial speed + Acceleration × Time

Q. Water flows into a cylindrical beaker at a constant rate. The base area of the beaker is 24 cm². The water level rises by 10 cm every second. How quickly will the water level rise in a beaker with a base area of 30 cm².

The flow of water in the beaker is 24 cm² × 10 cm/s = 240 cm³/s.

If the base area is 30 cm² then the rate of water level rise will be 240/30 = 8 cm/s

Q. A 2 kilowatt heater can boil a given amount of water in 10 minutes. How long will it take for a less powerful heater of 1.2 kilowatts to boil the same amount of water?

The heating required to boil the amount of water is 2 × 10 = 20 kilowatt minutes. At the rate of 1.2 kilowatt, this heat will be generated in 20/1.2 minutes = 16.66 minutes.

Q. A 2 kilowatt heater can boil a given amount of water in 10 minutes. How long will it take for a less powerful heater of 1.2 kilowatts to boil double the amount of water?

When the water is doubled, the heating required is also doubled. Hence, heating required = 40 kilowatt minutes. At the rate of 1.2 kilowatt, this heat will be generated in 40/1.2 = 33.33 minutes

Problems on clocks are based on the movement of the minute hand and that of the hour hand as well as on the relative movement between the two. It is best to solve problems on clocks by considering a clock to be a circular track having a circumference of 60 km and each kilometre being represented by one minute on the dial of the clock. Then, we can look at the minute hand as a runner running at the speed of 60 kmph while we can also look at the hour hand as a runner running at an average speed of 5 kmph.

Since, the minute hand and the hour hand are both moving in the same direction, the relative speed of the minute hand with respect to the hour hand is 55 kmph, that is, for every hour elapsed, the minute hand goes 55 km (minute) more than the hour hand.

Number of right angles formed by a clock:

A clock makes 2 right angles between any 2 hours. Thus, for instance, there are 2 right angles formed between 12 to 1 or between 1 and 2 or between 2 and 3 or between 3 and 4 and so on

However, contrary to expectations, the clock does not make 48 but 46 right angles in a day. This happens because whenever the clock passes between the time period 2–4 or between the time period 8–10 there are not 4 but only 3 right angles.

This happens because the second right angle between 2–3 (or 8–9) and the first right angle between 3–4 (or 9–10) are one and the same, occurring at 3 or 9.

Exactly the same situation holds true for the formation of straight lines. There are 2 straight lines in every hour. However, the second straight line between 5–6 (or 11–12) and the first straight line between 6–7 (or 12–1) coincide with each other and are represented by the straight line formed at 6 (or 12)

Q. At what time between 2–3 p.m. is the first right angle in that time formed by the hands of the clock?

At 2 p.m. the minute hand can be visualised as being 10 kilometres behind the hour hand. (considering the clock dial to be a race track of circumference 60 km such that each minute represents a kilometre).

Also, the first right angle between 2–3 is formed when the minute hand is 15 kilometres ahead of the hour hand.

Thus, the minute hand has to cover 25 kilometres over the hour hand. If the minute hand covers 55 km over the hour hand in 60 mins. Then it takes 5/11 of an hour which is = 27 (3/11) minutes to cover 25 km.

Hence, the required answer is: 2 : 27 : 16.36 seconds.

The relative speed of two bodies moving around a circle in the same direction is taken as S1 – S2. Also, when two bodies are moving around a circle in the opposite direction, the speed of the two bodies is taken to be S1 + S2

Three or more bodies start moving simultaneously from the same point on the circumference of the circle, in the same direction around the circle. They will first meet again in the LCM of the times that the fastest runner takes in totally overlapping each of the slower runners.

For instance, if A, B, C and D start clockwise from a point X on the circle such that A is the fastest runner hen we can define T_AB as the time in which A completely overlaps B, T_AC as the time in which A completely overlaps C and T_AD as the time in which A completely overlaps D. Then the LCM of T_AB , T_AC and T_{AD will be the time in which A, B, C and D will be together again for the first time}.

if A, B and C start from a point X on the circle such that T_A , T_B and T_C are the times in which A, B and C respectively cover one complete round around the circle, then they will all meet together at the starting point in the LCM of T_A , T_B and T_C.

The Sinhagad Express left Pune at noon sharp. Two hours later, the Deccan Queen started from Pune in the same direction. The Deccan Queen overtook the Sinhagad Express at 8 p.m. Find the average speed of the two trains over this journey if the sum of their average speeds is 70 km/h.

34.28

Ans .

34.28

Explanation :

The ratio of time for the travel is 4:3 (Sinhagad to Deccan Queen). Hence, the ratio of speeds would be 3:4. Since, the sum of their average speeds is 70 kmph, their respective speeds would
be 30 and 40 kmph respectively. Use alligation to get the answer as 34.28 kmph

Walking at 3/4 of his normal speed, Abhishek is 16 minutes late in reaching his office. The usual time taken by him to cover the distance between his home and his office is

Ans .

Explanation :

When speed goes down to three fourth (i.e. 75%) time will go up to 4/3rd
(or 133.33%) of the original time. Since, the extra time required is 16 minutes, it should be equated to 1/3
rd of the normal time. Hence, the usual time required will be 48 minutes.

Ram and Bharat travel the same distance at the rate of 6 km per hour and 10 km per hour respectively. If Ram takes 30 minutes longer than Bharat, the distance travelled by each is

7.5

Ans .

7.5

Explanation :

Since, the ratio of speeds is 3:5, the ratio of times would be 5:3. The difference in the times would be 2 (if looked at in the 5:3 ratio context.) Further, since Ram takes 30 minutes longer, 2
corresponds to 30. Hence, using unitary method, 5 will correspond to 75 and 3 will correspond to
45 minutes. Hence at 10 kmph, Bharat would travel 7.5 km

Two trains for Mumbai leave Delhi at 6 : 00 a.m. and 6 : 45 am and travel at 100 kmph and 136 kmph respectively. How many kilometres from Delhi will the two trains be together?

262.4

260

283.33

275

Ans .

283.33

Explanation :

The train that leaves at 6 am would be 75 km ahead of the other train when it starts. Also, the relative speed being 36 kmph, the distance from Mumbai would be:
(75/36) × 136 = 283.33 km

Two trains, Calcutta Mail and Bombay Mail, start at the same time from stations Kolkata and Mumbai respectively towards each other. After passing each other, they take 12 hours and 3 hours to reach Mumbai and Kolkata respectively. If the Calcutta Mail is moving at the speed of 48 km/h, the speed of the Bombay Mail is

Ans .

Explanation :

If two trains (or bodies) start at the same time from points A and B towards each other and after crossing they take a and b sec in reaching B and A respectively, then (A's speed) : (B’s speed) = b^ 1/2 : a^1/2. so we get Hence, the Bombay Mail would travel at 96 kmph.

Shyam’s house, his office and his gym are all equidistant from each other. The distance between any 2 of them is 4 km. Shyam starts walking from his gym in a direction parallel to the road connecting his office and his house and stops when he reaches a point directly east of his office. He then reverses direction and walks till he reaches a point directly south of his office. The total distance walked by Shyam is

Ans .

Explanation :




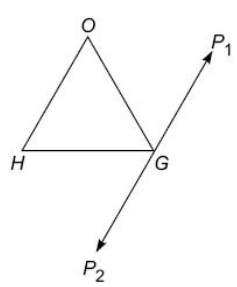
From the figure above we see that Shyam would have walked a distance of 4 + 4 + 4 = 12 km. (G to P1, P1 to G and G to P2).

Lonavala and Khandala are two stations 600 km apart. A train starts from Lonavala and moves towards Khandala at the rate of 25 km/h. After two hours, another train starts from Khandala at the rate of 35 km/h. How far from Lonavala will they will cross each other?

250

300

279.166

475

Ans .

279.166

Explanation :

When the train from Khandala starts off, the train from Lonavala will already have covered 50 kms. Hence, 550 km at a relative speed of 60 kmph will take 550/60 hrs. From this, you can get
the answer as: 50 + (550/60) * 25 = 279.166 km

Walking at 3/4 of his normal speed, a man takes 2(1/2) hours more than the normal time. Find the normal time.

7.5

Ans .

7.5

Explanation :

When his speed becomes 3/4th , his time would increase by 1/3rd
. Thus, the normal time = 7.5 hrs. (since increased time = 2.5 hrs).

Alok walks to a viewpoint and returns to the starting point by his car and thus takes a total time of 6 hours 45 minutes. He would have gained 2 hours by driving both ways. How long would it have taken for him to walk both ways?

8 h 45 min

7 h 45 min

5 h 30 min

6 h 45 min

Ans .

8 h 45 min

Explanation :

Since he gains 2 hours by driving both ways (instead of walking one way) the time taken for driving would be 2 hours less than the time taken for walking. Hence, he stands to lose another
two hours by walking both ways. Hence his total time should be 8 hrs 45 minutes.

Sambhu beats Kalu by 30 metres or 10 seconds. How much time was taken by Sambhu to complete a race 1200 meters.

6 min 30 s

3 min 15 s

12 min 10 s

2 min 5 s

Ans .

6 min 30 s

Explanation :

Kalu’s speed = 3 m/s.
For 1200 m, Kalu would take 400 seconds and Sambhu would take 10 seconds less. Hence, 390
seconds

Ram and Shyam run a race of 2000 m. First, Ram gives Shyam a start of 200 m and beats him by 30 s. Next, Ram gives Shyam a start of 3 min and is beaten by 1000 metres. Find the time in minutes in which Ram and Shyam can run the race separately.

8, 10

4, 5

5, 9

6, 9

Ans .

 4, 5

Explanation :

When Ram runs 2000 m, Shyam runs (1800 – 30s)
When Ram runs 1000 m, Shyam runs (2000 – 180s).
Then: 2000/1000 = 1800 - 30s / 2000 - 180s
Solving , we get s = 6.66 m/s
Thus, Shyam’s speed = 400 m/minute and he would take 5 minutes to cover the distance. Option (b) fits.

A starts from a point that is on the circumference of a circle, moves 600 metre in the North direction and then again moves 800 metre East and reaches a point diametrically opposite the starting point. Find the diameter of the circle?

1000 m

500 m

800 m

900 m

Ans .

1000 m

Explanation :

The diameter of the circle would be given by the hypotenuse of the right triangle with legs 600 and
800 respectively. Hence, the required diameter = 1000 meters.

X and Y are two stations 600 km apart. A train starts from X and moves towards Y at the rate of 25 km/h. Another train starts from Y at the rate of 35 km/h. How far from X they will cross each other?

250 km

300 km

450 km

475 km

Ans .

250 km

Explanation :

The distance would get divided in the ratio of speeds (since time is constant). Thus, the distance
ratio would be 5 : 7 and required distance = 5/12 × 600 = 250 km.

Two trains A and B start from station X to Y, Y to X respectively. After passing each other, they take 12 hours and 3 hours to reach Y and X respectively. If train A is moving at the speed of 48 km/h, the speed of train B is

24 km/h

96 km/h

21 km/h

20 km/h

Ans .

96 km/h

Explanation :

The time taken before their meeting would be given by t
2 = 12 × 3 = 36 Æ t = 6 hours. This means
that their ratio of speeds is 1:2. Since train A is traveling slower, the speed of train B would be
double the speed of train A. Required answer = 48 × 2 = 96.

Two trains for Patna leave Delhi at 6 a.m. and 6:45 a.m. and travel at 98 kmph and 136 kmph respectively. How many kilometres from Delhi will the two trains meet?

262.4 km

260 km

200 km

None of these

Ans .

None of these

Explanation :
```
[73.5 × 136]/38.
```

A and B travel the same distance at the rate of 8 kilometre and 10 kilometre an hour respectively. If A takes 30 minutes longer than B, the distance travelled by B is

6 km

10 km

16 km

20 km

Ans .

20 km

Explanation :

Solve using options. The value in option (d) fits the situation as 20/8 – 20/10 = 2.5 – 2 = 0.5 hours = 30 minutes.

Walking at 3/4 of his usual speed, a man is 16 minutes late for his office. The usual time taken by him to cover that distance is

48 m

60 m

42 min

62 m

Ans .

48 m

Explanation :

At 3/4th speed, extra time = 1/3
rd of time = 16 minutes. Normal time = 48 minutes.

Two cars started simultaneously toward each other from town A and B, that are 480 km apart. It took the first car travelling from A to B 8 hours to cover the distance and the second car travelling from B to A 12 hours. Determine at what distance from A the two cars meet.

288 km

200 km

300 km

196 km

Ans .

288 km

Explanation :

The speed of the first car would be 60 kmph while the speed of the second car would be 40 kmph.
The relative speed of the two cars would be 100 kmph. To cover 480 km they would take 480/100
= 4.8 hours Æ In 4.8 hours, the car traveling from A to B would have traveled 4.8 × 60 = 288 kms

A car travels 1/3 of the distance on a straight road with a velocity of 10 km/h, the next 1/3 with a velocity of 20 km/h and the last 1/3 with a velocity of 60 km/h. What is the average velocity of the car for the whole journey?

18 km/h

10 km/h

20 km/h

15 km/h

Ans .

18 km/h

Explanation :

Assume a distance of 60 km in each stretch. Get the average speed by the formula. Total distance/
Total time = 180/10 = 18 kmph.

A person travelled a distance of 200 kilometre between two cities by a car covering the first quarter of the journey at a constant speed of 40 km/h and he remaining three quarters at a constant speed of x km/h. If the average speed of the person for the entire journey was 53.33 km/h what is the value of x?

55 km/h

60 km/h

70 km/h

80 km/h

Ans .

60 km/h

Explanation :

The total time taken by the motorist would be 200/53.333 = 200 × 3/160 = 3.75 hours = 3 hours 45 minutes. In the first half of the journey the motorist covers 1/4th the distance @ 40kmph. This
means that he takes 50/40 = 1.25 hours = 1 hour 15 minutes in covering the first 50 kms. This also
means that he covers the remaining distance of 150 km in 2 hours 30 minutes so a speed of 60
kmph. Hence, option (b) is correct

A cyclist moving on a circular track of radius 100 metres completes one revolution in 2 minutes. What is the average speed of cyclist (approximately)?

314 m/minute

200 m/minute

300 m/minute

900 m/minute

Ans .

314 m/minute

Explanation :

The length of the circular track would be equal to the circumference of the circle. In 2 minutes
thus, the cyclist covers 3.14 × 200 = 628 meters (using the formula for the circumference of a
circle).
Thus, the cyclist’s speed would be 628/2 = 314 meters/minute.

A train moves at a constant speed of 120 km/h for one kilometre and at 40 kmph for the next one kilometre. What is the average speed of the train?

48 kmph

50 kmph

80 kmph

60 kmph

Ans .

60 kmph

Explanation :

The average speed would be given by: 120 * 1* 40 * 3 / 4 =
= 60 kmph

A plane left half an hour later than the scheduled time and in order to reach its destination 1500 kilometre away in time, it had to increase its speed by 33.33 per cent over its usual speed. Find its increased speed.

250 kmph

500 kmph

750 kmph

1000 kmph

Ans .

1000 kmph

Explanation :

By increasing the speed by 33.33%, it would be able to reduce the time taken for travel by 25%.
But since this is just able to overcome a time delay of 30 minutes, 30 minutes must be equivalent
to 25% of the time originally taken. Hence, the original time must have been 2 hours and the
original speed would be 750 kmph. Hence, the new speed would be 1000 kmph.

If Arun had walked 1 km/h faster, he would have taken 10 minutes less to walk 2 kilometre. What is Arun’s speed of walking?

1 kmph

2 kmph

3 kmph

6 kmph

Ans .

3 kmph

Explanation :

Solve through options using trial and error. For usual speed 3 kmph we have:
Normal time Æ 2/3 hours = 40 minutes.
At 4 kmph the time would be 2/4 hrs, this gives us a distance of 10 minutes. Hence option (c) is
correct

A passenger train takes 2 h less for a journey of 300 kilometres if its speed is increased by 5 kmph over its usual speed. Find the usual speed.

10 kmph

12 kmph

20 kmph

25 kmph

Ans .

25 kmph

Explanation :

The required speed s would be satisfying the equation:
300/s – 300/(s + 2) = 5
Solving for s from the options it is clear that s = 25

A journey of 192 km takes 2 hours less by a fast train than by a slow train. If the average speed of the slow train be 16 kmph less than that of fast train, what is the average speed of the faster train?

32 kmph

16 kmph

12 kmph

48 kmph

Ans .

48 kmph

Explanation :

Solve this question using the values given in the options. Option (d) can be seen to fit the situation
given by the problem as it gives us the following chain of thought:
If the average speed of the faster train is 48 kmph, the average speed of the slower train would be
32 kmph. In this case, the time taken by the faster train (192/48 = 4 hours) is 2 hours lesser than
the time taken by the slower train (192/32 = 6 hours). This satisfies the condition given in the
problem and hence option (d) is correct

Harsh and Vijay move towards Hosur starting from IIM, Bangalore, at a speed of 40 km/h and 60 km/h respectively. If Vijay reaches Hosur 200 minutes earlier then Harsh, what is the distance between IIM, Bangalore, and Hosur?

600 km

400 km

900 km

200 km

Ans .

400 km

Explanation :

At 40 kmph, Harsh would cover (200/60) × 40 km.
= 400/3 km. = 133.33 km.
This represents the distance by which Vijay would be ahead of Harsh, when Vijay reaches the
endpoint means in essence that Vijay must have travelled for 133.33/20 hours Æ 6.66 hours
Hence, the distance is 60 × 6.66 = 400 km

A car driver, driving in a fog, passes a pedestrian who was walking at the rate of 2 km/h in the same direction. The pedestrian could see the car for 6 minutes and it was visible to him up to a distance of 0.6 km. What was the speed of the car?

30 km/h

15 km/h

20 km/h

8 km/h

Ans .

8 km/h

Explanation :

In 6 minutes, the car goes ahead by 0.6 km. Hence, the relative speed of the car with respect to the
pedestrian is equal to 6 kmph, since, the pedestrian is walking at 2 kmph, hence, the net speed is 8
kmph.

Vinay fires two bullets from the same place at an interval of 12 minutes but Raju sitting in a train approaching the place hears the second report 11 minutes 30 seconds after the first. What is the approximate speed of train (if sound travels at the speed of 330 metre per second)?

660/23 m/s

220/7 m/s

330/23 m/s

110/23 m/s

Ans .

330/23 m/s

Explanation :

Two trains A and B start simultaneously in the opposite direction from two points A and B and arrive at their destinations 9 and 4 hours respectively after their meeting each other. At what rate does the second train B travel if the first train travels at 80 km per hour.

60 km/h

100 km/h

120 km/h

80 km/h

Ans .

120 km/h

Explanation :
```
direct formula based questions
```

A railway passenger counts the telegraph poles on the rail road as he passes them. The telegraph poles are at a distance of 50 metres. What will be his count in 4 hours, if the speed of the train is 45 km per hour?

600

2500

3600

5000

Ans .

Explanation :

In four hours, the train will travel 180 km (180,000 metres). The number of poles would be
180,000/50 = 3600.

Manish travels a certain distance by car at the rate of 12 km/h and walks back at the rate of 3 km/h. The whole journey took 5 hours. What is the distance he covered on the car?

12 km

30 km

15 km

6 km

Ans .

12 km

Explanation :

You can solve this question using the options. Option (a) fits the given situation best as if we take
the distance as 12 km he would have taken 1 hour to go by car and 4 hours to come back walking
—a total of 5 hours as given in the problem.

Sujit covers a distance in 40 minutes if he drives at a speed of 60 kilometer per hour on an average. Find the speed at which he must drive at to reduce the time of the journey by 25%?

60 km/h

70 km/h

75 km/h

80 km/h

Ans .

80 km/h

Explanation :

To reduce the time of the journey by 25%, he should increase his speed by 33.33% or 1/3rd
. Thus,required speed = 80 kmph.

A motor car does a journey in 17.5 hours, covering the first half at 30 km/h and the second half at 40 km/h. Find the distance of the journey.

684 km

600 km

120 km

540 km

Ans .

600 km

Explanation :

If the car does half the journey @ 30 kmph and the other half at 40 kmph it’s average speed can be
estimated using weighted averages.
Since, the distance traveled in each part of the journey is equal, the ratio of time for which the car
would travel would be inverse to the ratio of speeds. Since, the speed ratio is 3:4, the time ratio
for the two halves of the journey would be 4:3. The average speed of the car would be:
(30 × 4 + 40 × 3)/7 = 240/7 kmph.
It is further known that the car traveled for 17.5 hours (which is also equal to 35/2 hours).
Thus, total distance = average speed × total time = (240 × 35)/(2 × 7) = 120 × 5 = 600 km

Jayshree goes to office at a speed of 6 km/h and returns to her home at a speed of 4 km/h. If she takes 10 hours in all, what is the distance between her office and her home?

24 km

12 km

10 km

30 km

Ans .

24 km

Explanation :
```
d/6 + d/4 = 10 Æ d = 24 km
```

Narayan Murthy walking at a speed of 20 km/h reaches his college 10 minutes late. Next time he increases his speed by 5 km/h, but finds that he is still late by 4 minutes. What is the distance of his college from his house?

20 km

6 km

12 km

None of these

Ans .

10 km

Explanation :

By increasing his speed by 25%, he will reduce his time by 20%. (This corresponds to a 6 minute
drop in his time for travel—since he goes from being 10 minutes late to only 4 minutes late.)
Hence, his time originally must have been 30 minutes. Hence, the required distance is 20 kmph ×
0.5 hours = 10 km

Rishikant, during his journey, travels for 20 minutes at a speed of 30 km/h, another 30 minutes at a speed of 50 km/h, and 1 hour at a speed of 50 km/h and 1 hour at a speed of 60 km/h. What is the average velocity

51.18 km/h

63 km/h

39 km/h

48 km/h

Ans .

51.18 km/h

Explanation :

The distance covered in the various phases of his travel would be:
10 km + 25 km + 50 km + 60 km. Thus the total distance covered = 145 km in 2 hours 50 minutes
so
145 km in 2.8333 hours so 51.18 kmph

Rajdhani Express travels 650 km in 5 h and another 940 km in 10 h. What is the average speed of train?

1590 km/h

168 km/h

106 km

126 km/h

Ans .

106 km

Explanation :

Total distance/Total time = 1590/15 = 106 kmph

Without stoppage, a train travels a certain distance with an average speed of 60 km/h, and with stoppage, it covers the same distance with an average speed of 40 km/h. On an average, how many minutes per hour does the train stop during the journey?

20 min/h

15 min/h

10 min/h

40 min/h

Ans .

40 min/h

Explanation :

Since the train travels at 60 kmph, it’s speed per minute is 1 km per minute. Hence, if it’s speed with stoppages is 40 kmph, it will travel 40 minutes per hour.

What is the time taken by Chandu to cover a dis- ance of 360 km by a motorcycle moving at a speed of 10 m/s?

Ans .

Explanation :

Since Chandu is moving at a speed of 10 m/s and he has to cover 360 km or 360000 meters, the
time taken would be given by 360000/10 seconds = 36000 seconds = 36000/60 minutes = 600
minutes = 10 hours.

A motorboat whose speed in still water is 15 kmph goes 30 km downstream and comes back in a total 4 hours 30 min. Determine the speed of the stream

2 kmph

3 kmph

4 kmph

5 kmph

Ans .

5 kmph

Explanation :

30/(15 + x) + 30/(15 – x) = 4 hrs 30 minutes.
At x = 5, the equation is satisfied.

In a race of 600 meters, Ajay beats Vijay by 60 metres and in a race of 500 meters Vijay beats Anjay by 25 meters. By how many meters will Ajay beat Anjay in a 400 meter race?

48 m

52 m

56 m

58 m

Ans .

58 m

Explanation :

When Ajay does 600 metres, Vijay does 540 m.
When Vijay does 500 metres, Anjay does 475 m
Thus, Ajay : Vijay : Anjay = 600 : 540 : 513.
Thus, Ajay would beat Anjay by (87 × 2/3) = 58 m in a 400 m race

A motorboat whose speed in still water is 10 km/h went 91 km downstream and then returned to its starting point. Calculate the speed of the river flow if the round trip took a total of 20 hours

3 km/h

4 km/h

6 km/h

8 km/h

Ans .

3 km/h

Explanation :

Look for the solution by thinking of the factors of 91. It can be seen that 91/13 + 91/7 = 7 + 13 =
20 hours. This means that the speed of the boat in still water is 10 kmph and the speed of the water
flow would be 3 kmph. Option (a) is correct

A motorboat went down the river for 14 km and then up the river for 9 km. It took a total of 5 hours for the entire journey. Find the speed of the river flow if the speed of the boat in still water is 5 km/h

1 kmph

l.5 kmph

2 kmph

3 kmph

Ans .

2 kmph

Explanation :

14/(5 + x) + 9/(5 – x) = 5
x = 2, fits this equation

At what time are the hands of clock together between 2 and 3 p.m.?

2/11 hours past 2 p.m.

2/9 hours past 2 p.m.

2:10 p.m.

None of these

Ans .

2/11 hours past 2 p.m.

Explanation :

If we consider the clock to be a circle with circumference 60 km, the speed of the Minute hand =
60 kmph, while the speed of the hour hand = 5 kmph. The relative speed = 55 kmph. At 2 PM, the
distance between the two would be seen as 10 km. This would get covered in 10/55 = 2/11 hours.
Option (a) is correct.

Between 5 a.m. and 5 p.m. of a particular day for how many times are the minute and the hour hands together?

Ans .

Explanation :

The hands would be together once in each hour. However, the 12 noon time would be counted in
both 11 to 12 and 12 to 1. Hence, the no. of times = 12 – 1 = 11.

The length of the minutes hand of a clock is 8 cm. Find the distance travelled by its outer end in 15 minutes

4p cm

8p cm

12p cm

16p cm

Ans .

4p cm

Explanation :
```
(1/4) × 2pr = 4p (Since r = 8 cm).
```

A man goes down stream at x km/h and upstream at y km/h. The speed of the boat in still water is

0.5 (x + y)

0.5 (x – y)

x + y

x - y

Ans .

0.5 (x + y)

Explanation :

The speed of the boat in still water is the average of the upstream and downstream speeds. (x + y)/2

In a stream that is running at 2 km/h, a man goes 10 km upstream and comes back to the starting point in 55 minutes. Find the speed of the man in still water.

20 km/h

22 km/h

24 km/h

28 km/h

Ans .

22 km/h

Explanation :

10/(x – 2) + 10/(x + 2) = 55/60 = 11/12 hours.
x = 22 fits the expression.

A man can row 30 km upstream and 44 km downstream in 10 hours. It is also known that he can row 40 km upstream and 55 km downstream in 13 hours. Find the speed of the man in still water.

4 km/h

6 km/h

8 km/h

12 km/h

Ans .

8 km/h

Explanation :

The given situations are satisfied with the speed of the boat as 8 kmph and the speed of the stream
as 3 kmph. Option (c) is correct.

A lazy man can row upstream at 16 km/h and downstream at 22 km/h. Find the man’s rate in still water (in kmph).

Ans .

Explanation :

Rate in still water = (16 + 22)/2 = 19 kmph

A dog is passed by a train in 8 seconds. Find the length of the train if its speed is 36 kmph

70 m

80 m

85 m

90 m

Ans .

80 m

Explanation :

The length of the train would be given by: 36 × 5/18 × 8 = 80 meters.

Subbu can row 6 km/h in still water. When the river is running at 1.2 km/h, it takes him 1 hour to row to a place and back. How far in the place?

2.88 km

2.00 km

3.12 km

2.76 km

Ans .

2.88 km

Explanation :

Upstream speed = 4.8 kmph
Downstream speed = 7.2 kmph.
d/4.8 + d/7.2 = 1
Solving we get d = 2.88 km.

Vijay can row a certain distance downstream in 6 h and return the same distance in 9 h. If the stream flows at the rate of 3 km/h, find the speed of Vijay in still water.

12 km/h

13 km/h

14 km/h

15 km/h

Ans .

12 km/h

Explanation :

Vijay takes 9 hours to return upstream after going for 6 hours downstream. Solve using options.
Option (d) fits as we get Downstream speed = 18 kmph Æ distance = 18 × 6 =108 km
Also, upstream speed = 12 kmph Æ distance = 12 × 9 = 108 km

A boat rows 16 km up the stream and 30 km downstream taking 5 h each time. The velocity of the current

1.1 km/h

1.2 km/h

1.4 km/h

1.5 km/h

Ans .

1.4 km/h

Explanation :

Upstream speed = 3.2 kmph
Downstream speed = 6 kmph.
Thus, speed of stream = 1.4 kmph.

Without stoppage, a train travels at an average speed of 75 km/h and with stoppages it covers the same distance at an average speed of 60 km/h. How many minutes per hour does the train stop?

10 m

12 m

14 m

18 m

Ans .

12 m

Explanation :

Speed of running of the train = 1.25 km/hr.
With stoppage, an effective speed of 60 kmph means that the time of travel per hour would be
60/1.25 = 48 minutes.
Thus, the train stops for 12 minutes per hour

Two trains for Howrah leave Muzaffarpur at 8:30 a.m. and 9:00 a.m. respectively and travel at 60 km/h and 70 km/h respectively. How many kilometres from Muzaffarpur will the two trains meet?

210 km

180 km

150 km

120 km

Ans .

210 km

Explanation :

When the second train leaves Muzaffarpur, the first train would have already traveled 30 km.
Now, after 9 AM, the relative speed of the two trains would be 10 kmph (i.e. the rate at which the
faster train would catch the slower train).
Since the faster train has to catch up a relative distance of 30 km in order for the trains to meet, it
would take 30/10 = 3 hours to catch up.
Distance from Muzaffarpur = 70 × 3 = 210 km

Two trains are travelling in the same direction at 50 km/h and 30 km/h respectively. The faster train crosses a man in the slower train in 18 seconds. Find the length of the faster train

0.1 km

1 km

1.5 km

1.4 km

Ans .

0.1 km

Explanation :
```
20 × (5/18) × 18 = 100 m = 0.1 km.
```

How many seconds will a caravan 120 metres long running at the rate 10 m/s take to pass a standing boy

Ans .

Explanation :

Distance to be covered = 120 meters. Speed = 10m/s Æ Time required = 120/10 =12 seconds.

In a 500 m race, the ratio of speed of two runners Vinay and Shyam is 3 : 4. If Vinay has a start of 140 m then Vinay wins by

Ans .

Explanation :

When Shyam does 500, Vinay does 375. Since Vinay has a start of 140 m, it means that Vinay only
needs to cover 360 m to reach the destination.
When Vinay does 360, Shyam would cover 480 m and lose by 20 m. (Since the ratio of their
speeds is 3 : 4)

At a game of billiards, A can give B 15 points in 60 and A can give C 20 in 60. How many points can B give C in a game of 90?

Ans .

Explanation :

Solve using options 1.33 m/s fits perfectly. When A scores 60 points B scores 45, and C scores
40.
Thus, when B scores 90, C would score 80. So, B can give C 10 points in 90

In a 100 m race, Shyam runs at 1.66 m/s. If Shyam gives Sujit a start of 4 m and still beats him by 12 seconds, what is Sujit’s speed?

1.11 m/s

0.75 m/s

1.33 m/s

1 km/h

Ans .

1.33 m/s

Explanation :

Solve using options 1.33 m/s fits perfectly.

Vinay runs 100 metres in 20 seconds and Ajay runs the same distance in 25 seconds. By what distance will Vinay beat Ajay in a hundred metre race?

10 m

20 m

25 m

12 m

Ans .

20 m

Explanation :

Speed of Vinay = 5 m/s, Speed of Ajay = 4m/s. In a hundred meter race, Vinay would take 20
seconds to complete and in this time Ajay would only cover 80 meters. Thus, Vinay beats Ajay by
20 meters in a hundred meter race.

Two trains pass each other on parallel lines. Each train is 100 metres long. When they are going in the same direction, the faster one takes 60 seconds to pass the other completely. If they are going in opposite directions they pass each other completely in 10 seconds. Find the speed of the slower train in km/h

30 km/h

42 km/h

48 km/h

60 km/h

Ans .

30 km/h

Explanation :

(Sf – Ss) × 60 = 200
Where Sf and Ss are speeds of the faster and slower train respectively
Æ Sf – Ss = 3.33
Also, (Sf + Ss) × 10 = 200.
Æ Sf + Ss = 20.
Solving we get Ss = 8.33 m/s
= 8.33 × 18/5 = 30 kmph.

In a stream, B lies in between A and C such that it is equidistant from both A and C. A boat can go from A to B and back in 6 h 30 minutes while it goes from A to C in 9 h. How long would it take to go from C to A?

3.75 h

4 h

4.25 h

4.5 h

Ans .

4 h

Explanation :

Since A to C is double the distance of A to B, it is evident that the time taken for A to C and back
would be double the time taken from A to B and back (i.e. double of 6.5 hours = 13 hours). Since
going from A to C takes 9 hours, coming back from C to A would take 4 hours (Since 9 + 4 = 13).

A boat goes 15 km upstream in 80 minutes. The speed of the stream is 5 km/h. The speed of the boat in still water is

16.25 km/h

16 km/h

15 km/h

17 km/h

Ans .

16.25 km/h

Explanation :

15 km upstream in 80 minutes Æ 15/1.33 = 11.25 kmph. (upstream speed of the boat).
Thus, still water speed of the boat
= 11.25 + 5 = 16.25 kmph

The speed of the boat in still water is 12 km/h and the speed of the stream is 2 km/h. A distance of 8 km, going upstream, is covered in

1 h

1 h 15 min

1 h 12 min

None of these

Ans .

None of these

Explanation :
```
8/(12 – 2) = 8/10 = 0.8 hours
```

Two trains are running on parallel lines in the same direction at speeds of 40 kmph and 20 kmph respectively. The faster train crosses a man in the second train in 36 seconds. The length of the faster train is

200 metres

185 metres

225 metres

210 metres

Ans .

200 metres

Explanation :
```
(20 × 5/18) × 36 = Lt so Lt = 200 m.
```

A boat goes 40 km upstream in 8 h and a distance of 49 km downstream in 7 h. The speed of the boat in still water is

5 km/h

5.5 km/h

6 km/h

6.5 km/h

Ans .

6 km/h

Explanation :

Upstream speed = 40/8 = 5 kmph.
Downstream speed = 49/7 = 7 kmph.
Speed in still water = average of upstream and downstream speed = 6 kmph.

A man rows 6 km/h in still water. If the river is running at 3 km per hour, it takes him 45 minutes to row to a place and back. How far is the place?

1.12 km

1.25 km

1.6875 km

2.5 km

Ans .

 1.6875 km

Explanation :

x/9 + x/3 = 3/4 Æ 4x/9 = 3/4 Æ x = 27/16 kms = 1.6875 kms.

A boat sails down the river for 10 km and then up the river for 6 km. The speed of the river flow is 1 km/h. What should be the minimum speed of the boat for the trip to take a maximum of 4 hours?

2 kmph

3 kmph

4 kmph

5 kmph

Ans .

4 kmph

Explanation :

Solve through options. For option (c) at 4 kmph, the boat would take exactly 4 hours to cover the
distance.

A boat sails downstream from point A to point B, which is 10 km away from A, and then returns to A. If the actual speed of the boat (in still water) is 3 km/h, the trip from A to B takes 8 hours less han that from B to A. What must the actual speed of the boat for the trip from A to B to take exactly 100 minutes?

1 km/h

2 km/h

3 km/h

4 km/h

Ans .

4 km/h

Explanation :

In order to solve this, you first need to think of the speed of the river flow (if the speed of the boat
in still water is 3 kmph). If we take the speed of the river flow as s, we get downstream speed as
3 + s and upstream speed as 3 – s.
10/(3 – s) – 10/(3 + s) = 8 hours Æ s = 2kmph.
Note: It is obvious that since the difference between the downstream time and the upstream time is
8 hours, the upstream and downstream speeds would both be factors of 10. The only value of s
such that both 3 + s and 3 – s are factors of 10 is s = 2.
If the boat needs to reach 10 km downstream in 100 minutes (1.66 hours) it means: 10/1.66 = 6
kmph is the downstream speed.
Since, the speed of the stream is 2 kmph, the required speed of the boat = 4 kmph

A train requires 7 seconds to pass a pole while it requires 25 seconds to cross a stationary train which is 378 metres long. Find the speed of the train.

75.6 km/h

75.4 km/h

76.2 km/h

21 km/h

Ans .

75.6 km/h

Explanation :

7 × St = Lt
25 × St = Lt + 378
Solving,St = 21 m/sec.
= 21 × 18/5 = 75.6 kmph.

A motorboat went downstream for 28 km and immediately returned. It took the boat twice as long to make the return trip. If the speed of the river flow were twice as high, the trip downstream and back would take 672 minutes. Find the speed of the boat in still water and the speed of the river flow.

9 km/h, 3 km/h

9 km/h, 6 km/h

8 km/h, 2 km/h

12 km/h, 3 km/h

Ans .

9 km/h, 3 km/h

Explanation :

From the situation described in the first condition itself we can see that the speed of coming back
has to be double the speed of going downstream. Checking the options, only option (a) fits this
condition i.e. Downstream speed = 2 × Upstream speed.
Hence, option (a) is correct.

upscfever.com

Chapter 12: TIME, SPEED AND DISTANCE

Formulae

Problems on Trains and Poles

Boats and Streams

Concept of Acceleration

Clocks

Circular motion: A special case of movement is when two or more bodies are moving around a circular track.

Solved Question Papers

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments