Let hypotenuse = x cm
Then, by Pythagoras theorem:
x2 = (48020)2 + (36015)2
x so 60025 cm

Let one side of the △ be = a Perimeter of equilateral triangle = 3a 3a = 72\( \sqrt{3} \) = a = 24\( \sqrt{3} \) cm Height = AC; by Pythagoras theorem AC² = a² – (a/2)² AC = 36 cm

Let inner radius = A; then 2pr = 440 so p = 70
Radius of outer circle = 70 + 14 = 84 cm
 Outer diameter = 2 × Radius = 2 × 84 = 168

Let inner radius = r and outer radius = R
Width = R – r = 396/2π - 352/2π
so (R – r) = 44/2π = 7 meters

Let outer radius = R; then inner radius = r = R – 7
2pR = 220 so 35m;
r = 35 – 7 = 28 m
Area of torch = pR2 – pr2 p(R2 – r2) = 1386 m2
Cost of traveling it = 1386 × = ` 693

Circumference of circle = 2pr = 44
= r = 7 cm
Area of a quadrant = π * r2 / 4 = 38.5 cm2

Volume of soil removed = l × b × h
= 7.5 × 6 × 1.5 = 67.5 m3

The longest pole can be placed diagonally (3-dimensional) 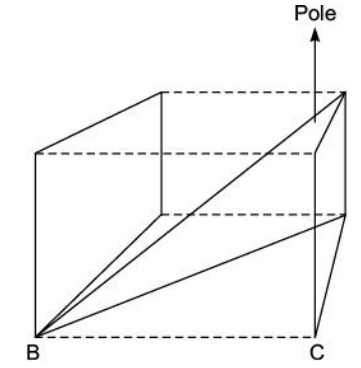BC = \( \sqrt{18^2 + 24^2} \)= 30 AC = \( \sqrt{30^2 + 16^2} \) = 34 m

(d)
Let the common ratio be = x
Then; length = 3x, breadth = 2x and height = x
Then; as per question 3x * 2x * x = 1296 so 6x3 = 1296
fi x = 6 m
Breadth = 2x = 12 m

Data is inadequate as it’s not mentioned that what part of the cube is melted to form cylinder

(b)
Let the common ratio be = x
Then, length = 4x, breadth = 3x and height = 2x
As per question;
2(4x * 3x + 3x * 2x + 2x * 4x) = 8788
2(12x2 + 6x2 + 8x2) = 8788 fi 52x2 = 8788
fi x = 13
Length = 4x = 52 cm

The total volume will remain the same, let the side of the resulting cube be = a. Then,
63 + 83 + 103 = a3
fi a = cube root of 1728 = 12 cm

Slant length = l = \( \sqrt{6^2 + 8^2} \)= 10 cm Then curved surface area = prl = p × 6 × 10 so 60p And total surface area = prl + pr² so p((6 × 10) + 6²) = 96p

Volume of a cone = π * r2 * h / 3
Then;100p = π * r2 * 12 / 3 = fi r = 5 cm
Curved surface area = prl
l = √ h2 + r2 = √ 52 + 122 = 13
then,prl = p × 13 × 5 = 65p cm2

(d)
Let the radius of the two cones be = x cm
Let slant height of 1st cone = 5 cm and
Slant height of 2nd cone = 7 cm
Then ratio of covered surface area = 5π / 7π = 5 : 7

Radius = π * r * l / π * l  = 2376 / 3.14 * 18 = 42 cm
Diameter = 2 × Radius = 2 × 42 = 84 cm

Let the radius of cylinder = 1(r)
Then the radius of cone be = 2(R)
Then as per question = π * r2*h / π * R2*h / 3 = 3 * π * r2*h / π * R2*h
so 3 : 4

The perimeter would remain the same in any case.
Let one side of a square be = a cm
Then a2 = 484 fi a = 22 cm \ perimeter = 4a = 88 cm
Let the radius of the circle be = r cm
Then 2pr = 88 fi r = 14 cm
Then area = pr2 = 616 cm2

Let the radius of the circle be = p
Then 2pr – 2r = 16.8 fi r = 3.92 cm
Then 2pr = 24.6 cm

Let the radius of the wheel be = p
Then 5000 × 2pr = 1100000 cm fi r = 35 cm

Let the slant height be = l
Let radius = r
Then v = π * r2 * h/3 = so r = √ 3v/πh = fi = 5 cm
l = √(h2 + l2) = √(122 + 52) = 13 cm

In 4 days, the short hand covers its circumference
4 × 2 = 8 times long hand covers its circumference
4 × 24 = 96 times
Then they will cover a total distance of:-
(2 × p × 4)8 + (2 × p × 6)96 fi 3818.24 cm

Let the radius of the smaller sphere = r Then, the radius of the bigger sphere = R Let the surface area of the smaller sphere = 1 Then, the surface area of the bigger sphere = 4 Then, as per question \( \frac{4\pir^2}{4\piR^2} = 1/4 , r/R = 1/2 \) and hence volumes = \( \frac{4\pir^3}{3} * \frac{3}{4\pi(2r)^3} = 1/8 \)

Inner radius(p) = 9/2 = 4.5 cm
Outer radius (R) = 10/2 = 5 cm
Volume of metal contained in the shell =  4πR3 – 4πr3 = 141.9
fi 141.9 cm3

Let smaller radius (r) = 1
Then bigger radius (R) = 2
Then, as per question
4πR2 / 4πr2 = (1/2)2 = 1 : 4

As per question 4πr3/3 = πr2h / 3 = 4r

Volume of wall = 1200 × 500 × 25 = 15000000 cm3
Volume of cement = 5% of 15000000 = 750000 cm3
Remaining volume = 15000000 – 750000 = 14250000 cm3
Volume of a brick = 25 × 12.5 × 7.5 = 2343.75 cm3
Number of bricks used = 14250000 / 2343.75 = 6080

Let the inner radius = r
Then 2pr = 352 m. Then r = 56
Then outer radius = r + 7 = 63 = R
Now,pR2 – pr2 = Area of road
= p(R2 – r2) = 2618 m2

1 hectare = 10000 m2
Height = 10 cm = 1/10m
Volume = 10000 × 1/10 = 1000 m3

Total surface area of 7 cubes so 7 × 6a2 = 1050
But on joining end to end, 12 sides will be covered.
So there area = 12 × a2 so 12 × 25 = 300
So the surface area of the resulting figure = 1050 – 300 = 750

Let the rise in height be = h
Then, as per the question, the volume of water should be equal in both the cases.
Now, 90 × 40 × h = 150 × 8
h = 150*8 / 90*40 = 1/3m = 100/3cm
= 33.33 cm

Slant height (l) = √(72 + 242)= 25 m
Area of cloth required = covered surface area of cone = prl = 22/7 × 7 × 25 = 550 m2
Amount of cloth required = 550/5 = 110 m

If the ratio of their diameters = 2 : 1, then the ratio of their radii will also be = 2 : 1
Let the radii of the broader cone = 2 and height be = 1
Then the radii of the smaller cone = 1 and height be = 2
Ratio of volumes = (π22*1 / 3) / (π12*2 / 3)
= 4π/3 * 3/2π = 2 : 1

Area of base = 6 × 10 = 60 m2
Volume of tent = 30 × 10 = 300 m3
Let the radius be = r, height = h, slant height = l
pr
2 = 60 fi r = √(60/π)
300 = πr2h/3 = 900 = p *60/π* h = h = 15 m

Volume of wood used = External volume – Outer Volume
fi (10 × 8 × 6) – (10 – 1) × (8 – 1) × (6 – 1)
fi 480 – (9 × 7 × 5) = 165 cm2

Total volume in both the cones will be equal. Let the number of smaller cubes = x
x * 33 = 24 × 9 × 8 fi x = 24*72/27 = 64

Let one side of the cube = a
Then a3 = 216 fi a = 6 m
Area of the resultant figure
= Area of all 3 cubes – Area of covered figure
fi 216 × 3 – (4 × a2) fi 648 – 144 fi 504 m2

Volume of metal used = 4πR3/3 - 4πr3/3
= 4π/3(123 – 103)
= 3047.89 cm3
Weight = volume × densityfi 4.9 × 3047.89
fi 14942.28 gm

Volume of cube = 7
3 = 343 cm3
Radius of cone = 7/2 = 3.5 cm
Height of cone = 7
Ratio of volumes = πr2h/3/343 = 11:42

The volume in both the cases will be equal. Let the height of cone be = h
4 × 22/7 × (14)3 × 1/3 = 22/7 * h/3 * (35/2)2
so 4(14)3 = h(35/2)2 = h = 35.84 cm

Diameter of circle = diagonal of square
= √(102 + 102)= 10√2
◊.◊ Radius = 5√2
Area of circle = pr2 = 50p = 50 × 3.14 = 157.14 cm3

Area of triangle = rS; where r = inradius S = 15+8+7/2 = 20 cm △ = \( \sqrt{s(s-a)(s-b)(s-c)} \) △ = 60 cm2 Area of triangle = rS; r = 3 cm

Circumference of the circular face of the cylinder = 2pr
fi 2 × 22/7 × 35/100 = 2.2 m
Number of revolutions required to lift the bucket by 11 m = 11/2.2 = 5

Surface area of the cube = 6a2 = 6 × (20)2
= 2400
Area of 6 circles of radius 10 cm = 6pr2
= 6 × p × 100
= 1885.71
Remaining area = 2400 – 1884 = 514.28

x * y * z = lb × bh × lh = (lbh)2
(V) Volume of a cuboid = lbh
So V2 = (lbh)2 = xyz

Diameter of the circle = diagonal of rectangle
= √(82 + 62) = 10 cm
Radius = 10/2 = 5 cm
Area of shaded portion = pr2 – lb = 3.14 × 52 – 8 × 6
= 30.57 cm2

Larger Radius (R) = 14 + 7 = 21 cm
Smaller Radius (r) = 7 cm
Area of shaded portion πR2θ/360 – πR2θ/360
π*θ/360 (212 - 72) = 102.67 cm

Area of quadrilateral = Area of right angled triangle + Area of equilateral triangle x = √(202 - 122)
= 16
Area of quadrilateral = 1/2*16*12 + √3/4 × 20 × 20
= 269 units2

h = √(242 - 132) = √407
volume = Area of base * height/3 = 18*26*√407/3 = 156√407

The perimeter would remain the same in both cases. Circumference of circle = 2pr = 2 × 22/7 × 28
= 176 cm
Perimeter of square = 176
Greatest side possible = 176/4 = 44 cm
Length of diagonal = √(442 + 442) = 62.216
= 88/2 * √2 = 44√2