-
Chapter 14 B: Coordinate Geometry
Formula
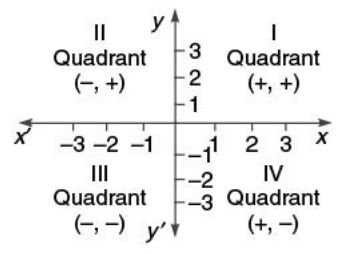
Let X'OX and Y’OY be two mutually perpendicular lines through any point O in the plane of the paper. Point O is known as the origin. The line X'OX is called the x-axis or axis of x; the line Y'OY is known as the y-axis or axis of y; and the two lines taken together are called the coordinate axes or the axes of coordinates.
Any point can be represented on the plane described by the coordinate axes by specifying its x and y coordinates. The x coordinate of the point is also known as the abscissa while the y coordinate is also known as the ordinate.
Distance Formula : If two points P and Q are such that they are represented by the points (x1, y1) and (x2, y2) on the x-y plane (cartesian plane), then the distance between the points P and Q = \( \sqrt{(x_1 - x_2)^2 - (y_1 - y_2)^2} \)
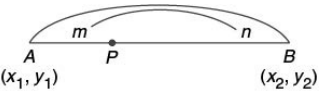
Section Formula : If any point (x, y) divides the line segment joining the points (x1, y1) and (x2, y2) in the ratio m : n internally, then x = (mx2 + nx1)/(m + n) and y = (my2 + ny1)/(m - n)
If any point (x, y) divides the line segment joining the points (x1, y1) and (x2, y2) in the ratio m : n externally, then x = (mx2 - nx1)/(m + n) and y = (my2 - ny1)/(m - n)
Area of a Triangle
The area of a triangle whose vertices are A (x1, y1), B (x2, y2) and C (x3, y3) is given by
\( \frac{x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)}{2} \)
Since the area cannot be negative, we have to take the modulus value given by the above equation
If one of the vertices of the triangle is at the origin and the other two vertices are A (x1, y1), B (x2, y2) , then the area of triangle is \( \frac{(x_1y_2 - x_2y_1)}{2} \)
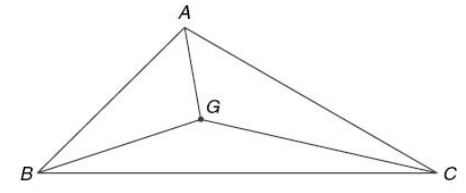
Centre of gravity or centroid of a triangle
The centroid of a triangle is the point of intersection of its medians (the line joining the vertex to the middle point of the opposite side).
Centroid divides the medians in the ratio 2 : 1.
In other words, the CG or the centroid can be viewed as a point at which the whole weight of the triangle is concentrated
If A (x1, y1), B (x2, y2) and C (x3, y3) are the coordinates of the vertices of a triangle, then the coordinates of the centroid G of that triangle are x = (x1 + x2 + x3)/3 and y = (y1 + y2 + y3)/3
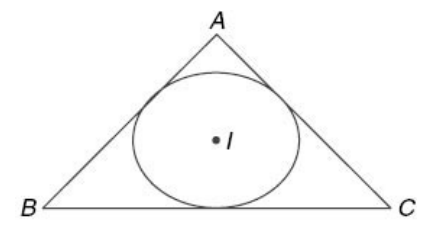
In-centre of a triangle
The centre of the circle that touches the sides of a triangle is called its Incentre. In other words, if the three sides of the triangle are tangential to the circle then the centre of that circle represents the in-centre of the triangle
The in-centre is also the point of intersection of the internal bisectors of the angles of the triangle. The distance of the in-centre from the sides of the triangle is the same and this distance is called the in-radius of the triangle.
IfA (x1, y1), B (x2, y2) and C (x3, y3) are the coordinates of the vertices of a triangle, then the coordinates of its in-centre are
\( x = \frac{ax_1 + bx_2 + cx_3}{a+b+c}, y = \frac{ay_1 + by_2 + cy_3}{a+b+c} \) where BC = a, AB = c and AC = b.
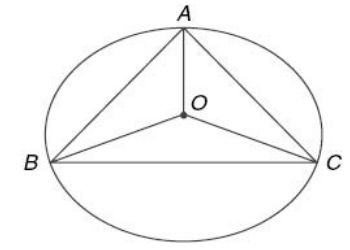
Circumcentre of a triangle
The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circumcentre
It is equidistant from the vertices of the triangle.
It is also known as the centre of the circle which passes through the three vertices of a triangle (or the centre of the circle that circumscribes the triangle.)
Let ABC be a triangle. If O is the circumcentre of the triangle ABC, then OA = OB = OC and each of these three represent the circum radius.
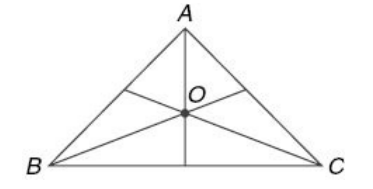
Orthocentre of a triangle
The orthocentre of a triangle is the point of intersection of the perpendiculars drawn from the vertices to the opposite sides of the triangle.
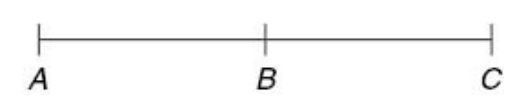
Collinearity of three points
Three given points A, B and C are said to be collinear, that is, lie on the same straight line, if any of the following conditions occur:
Area of triangle formed by these three points is zero
Slope of AB = Slope of AC
Any one of the three points (say C) lies on the straight line joining the other two points (here A and B).
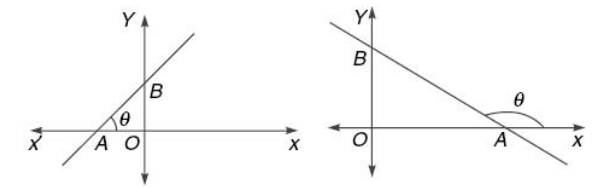
Slope of a line
The slope of a line joining two points A (x1, y1), B (x2, y2) is denoted by m and is given by m = (y2 – y1)/(x2 – x1) = tan q, where q is the angle that the line makes with the positive direction of x-axis.
This angle q is taken positive when it is measured in the anti-clockwise direction from the positive direction of the axis of x
Different Forms of the Equations of a Straight Line
General Form : The general form of the equation of a straight line is ax + by + c = 0. (First degree equation in x and y). Where a, b and c are real constants and a, b are not simultaneously equal to zero. In this equation, slope of the line is given by -a/b
The general form is also given by y = mx + c; where m is the slope and c is the intercept on y-axis. In this equation, slope of the line is given by m.
Line Parallel to the X-axis : The equation of a straight line parallel to the x-axis and at a distance b from it, is given by y = b. Obviously, the equation of the x-axis is y = 0
Line Parallel to Y-axis : The equation of a straight line parallel to the y-axis and at a distance a from it, is given by x = a. Obviously, the equation of y-axis is x = 0
Slope Intercept Form : The equation of a straight line passing through the point A (x1, y1) and having a slope m is given by (y – y1) = m (x – x1)
Two Points Form : The equation of a straight line passing through two points A (x1, y1), B (x2, y2) is given by \( (y - y_1) = \frac{(y_2 - y_1)(x - x_1)}{x_2 - x_1} \). Its slope = \( \frac{y_2 - y_1}{x_2 - x_1} \)
Intercept Form The equation of a straight line making intercepts a and b on the axes of x and y respectively is given by x/a + y/b = 1. If a straight line cuts x-axis at A and the y-axis at B then OA and OB are known as the intercepts of the line on x-axis and y-axis respectively
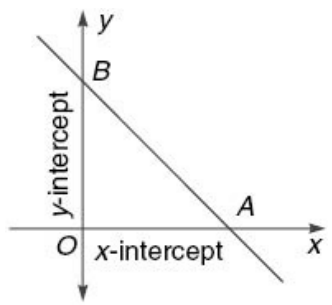
Perpendicularity and Parallelism
Condition for two lines to be parallel: Two lines are said to be parallel if their slopes are equal.
For this to happen, ratio of coefficient of x and y in both the lines should be equal.
In a general form, this can be stated as: line parallel to ax + by + c = 0 is ax + by + k = 0 or dx + ey + k = 0 if a/d = b/e where k is a constant
Length of perpendicular or Distance of a point from a line : The length of perpendicular from a given point (x1, y1) to a line ax + by + c = 0 is \( \frac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}} \)
Distance between two parallel lines.
If two lines are parallel, the distance between them will always be the same.
When two straight lines are parallel whose equations are ax + by + c = 0 and ax + by + c1 = 0, then the distance between them is given by
\( \frac{c - c_1}{\sqrt{a^2 + b^2}} \)
The length of the perpendicular from the origin to the line ax + by + c = 0 is given by \( \frac{c}{\sqrt{a^2 + b^2}} \)
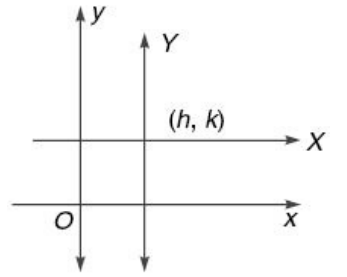
Change of axes
If origin (0, 0) is shifted to (h, k) then the coordinates of the point (x, y) referred to the old axes and (X, Y) referred to the new axes can be related with the relation x = X + h and y = Y + k
Point of intersection of two line : Point of intersection of two lines can be obtained by solving the equations as simultaneous equations.
If all the three vertices of a triangle have integral coordinates, then that triangle cannot be an Equilateral triangle.
Solved Question Papers
- Explanation :
Distance = \( \sqrt{(5-3)^2 + (2-4)^2} \)
- Explanation :
X = (2.1 + 1.2) /(1 + 2) = 4/3 Y = (2.2 + 1.5)/(2 + 1) = 9/3 = 3
- Explanation :
Area of triangle = |1/2 {0 (6– (–2)) + 3 ((–2) –4) + (–8) (4–6)}| = |1/2 {(0) + 3 (–6) + (–8) (–2)}| = |1/2 (–2)| = |–1| = 1 square unit.
- Explanation :
X coordinate = (5 + 4 + 8)/3 = 17/3 Y coordinate = (3 + 6 + 2)/3 = 11/3
- Explanation :
Obviously, the length of the two sides AB and BC of the triangle is 6 units and the length of the third side is (62 + 62)1/2. Hence a = c = 6, b = 6√2
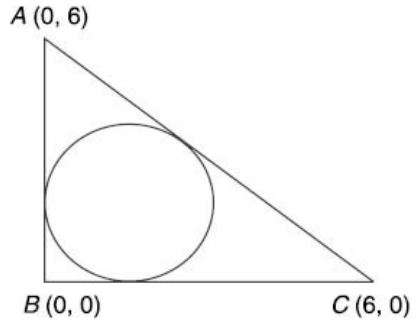
In-centre will be at X,Y = \( \frac{6*0 + 6√2 * 0 + 6*6}{6 + 6 + √2}, \frac{6*6 + 6√2 * 0 + 6*0}{6 + 6 + √2} \) so we get both X and Y as \( \frac{36}{12 + 6√2} \)
- Explanation :
Let ABC be the triangle whose sides AB, BC and CA have the equations 3x – y + 3 = 0, 3x + 4y + 3 = 0 and x + 3y + 11 = 0 respectively. Solving the equations, we get the points A, B and C as (–2, –3), (–1, 0) and (7, – 6) respectively. The equation of a line perpendicular to BC is 4x – 3y + k = 0. This will pass through (3, –3), the mid-point of BC, if 12 + 9 + k = 0 so k = –21 Putting k1 = –21 in 4x – 3y + k = 0, we get 4x – 3y – 21 = 0 as the equation of the perpendicular bisector of BC. Again, the equation of a line perpendicular to CA is 3x – y + k1 = 0. This will pass through (5/2, –9/2), the mid-point of AC if 15/2 + 9/2 + k1 = 0 fi k1 = –12 Putting k1 = –12 in 3x – y + k1 = 0, we get 3x – y – 12 = 0 as the perpendicular bisector of AC. Solving (i) and (ii), we get x = 3, y = –3. Hence, the coordinates of the circumcentre of △ABC are (3, –3).
- Explanation :
Let ABC be the triangle whose sides BC, CA and AB have the equations y = 15, 3x = 4y, and 5x + 12y = 0 respectively. Solving these equations pairwise, we get coordinates of A, B and C as (0, 0), (–36, 15) and (20, 15) respectively. AD is a line passing through A (0, 0) and perpendicular to y = 15. So, equation of AD is x = 0. The equation of any line perpendicular to 3x – 4y = 0 is represented by 4x + 3y + k = 0. This line will pass through (–36, 15) if –144 + 45 + k = 0 fi k = 99. So the equation of BE is 4x + 3y + 99 = 0. Solving the equations of AD and BE we get x = 0, y = – 33. Hence the coordinates of the orthocentre are (0, –33).
- Explanation :
Let A, B, C are the points whose coordinates are (–a, –b), (0, 0) and (a, b) Slope of BC = b/a Slope of AB = b/a So, the straight line made by points A, B and C is collinear. Alternative: Draw the points on paper assuming the paper to be a graph paper. This will give you an indication regarding the nature of points. In the above question, point (a, b) is in first quadrant for a > 0, b > 0 and point (–a, –b) is directly opposite to the point (a, b) in the third quadrant with the third point (0, 0) in the middle of the straight line joining the points A and B. You can check this by assuming any value for ‘a’ and ‘b’. Also, you can use this method for solving any problem involving points and diagrams made by those points. However you should be fast enough to trace the points on paper. A little practice of tracing points might help you
- Explanation :
Here slope = 1 And point given is (2, –3). So, we will use point-slope formula for finding the equation of straight line. This formula is given by: (y – y1) = m (x – x1) So, equation of the line will be y – (–3) = 1 (x – 2) fi y + 3 = x – 2 fi y – x + 5 = 0
- Explanation :
Go through the options and check which of the two lines given will satisfy the criteria for two lines to be parallel. It will be obvious that option c is correct, that is, the line 2x – 4y = 6 is parallel to the line x – 2y = 4.
- Explanation :
Equation of the line parallel to 3x + 4y = 7 will be of the form 3x + 4y = k. This line passes through (3, –3), so this point will satisfy the equation of straight line 3x + 4y = k. So, 3*3+ 4*(–3) = k fi k = –3. Hence, equation of the required straight line will be 3x + 4y + 3 = 0. Condition for two lines to be perpendicular: Two lines are said to be perpendicular if product of the slopes of the lines is equal to –1. For this to happen, the product of the coefficients of x + the product of the coefficients of y should be equal to zero.
- Explanation :
Check the equations to get option 4 as the correct answer.
- Explanation :
Equation of the line perpendicular to 3x + 4y = 7 will be of the form 4x – 3y = K. This line passes through (3, –3), so this point will satisfy the equation of straight line 4x – 3y = K. So, 4.3 – 3.–3 fi K = 21. Hence, equation of required straight line will be 4x – 3y = 21
- Explanation :
Obviously, the difference between the parallel lines will be the side of the square. To convert it into the form of finding the distance of a point from a line, we will have to find out a point at which any one of these two lines cut the axes and then we will draw a perpendicular from that point to the other line, and this distance will be the side of the square. To find the point at which the equation of the line x + y = 2 cut the axes, we will put once x = 0 and then again y = 0. When x = 0, y = 2, so the coordinates of the point where it cuts y-axis is (0, 2). Now the point is (0, 2), and the equation of line on which perpendicular is to be drawn is x + y = –2. So, distance = \( \frac{1*0 + 1*2 + 2}{\sqrt{1^2 + 1^2}} = \frac{4}{\sqrt{2}} \) Area = 16/2 = 8
- Explanation :
Let (X, Y) be the coordinates of the point in the new axis. Then, 1 = X + 5 so X = –4 2 = Y + 2 so Y = 0 So, the new coordinates of the point will be (–4, 0)