Inequalities - Aptitude

Chapter 14 D: Inequalities

Two real numbers or two algebraic expressions related by the symbol > (“Greater Than”) or < (“Less Than”) (and also by the signs ≥ or <= ) form an inequality.

A < B, A > B (are plain inequalities)

A ≥ B, A ≤ B (are called as inequations)

The inequality consists of two sides—the left hand side, A and the right hand side, B. A and B can be algebraic expressions or they can be numbers.

An inequality with the < or > sign is called a strict inequality while an inequality having ≥ or ≤ sign is called a slack inequality.

The expressions A and B have to be considered on the set where A and B have sense simultaneously.

This set is called the set of permissible values of the inequality.

If the terms on the LHS and the RHS are algebraic equations/identities, then the inequality may or may not hold true for a particular value of the variable/set of variables assumed

The direction in which the inequality sign points is called the sense of the inequality. If two or several inequalities contain the same sign (< or >) then they are called inequalities of the same sense. Otherwise they are called inequalities of the opposite sense.

Now let us consider some basic definitions about inequalities. For 2 real numbers a and b The inequality a > b means that the difference a – b is positive. The inequality a < b means that the difference a – b is negative.

For any two real numbers a and b, only one of the following restrictions can hold true: a = b, a > b or a < b

The inequality a ≥ b means that a > b or a = b, that is, a is not less than b. The inequality a ≤ b means that a < b or a = b, that is, a is not greater than b. We can also have the following double inequalities for simultaneous situations: a < b < c, a < b ≤ c , a ≤ b < c , a ≤ b ≤ c

1. If a > b then b < a and vice versa.

2. If a > b and b > c then a > c.

3. If a > b then for any c, a + c > b + c. In other words, an inequality remains true if the same number is added on both sides of the inequality.

4. Any number can be transposed from one side of an inequality to the other side of the inequality with the sign of the number reversed. This does not change the sense of the inequality.

5. If a > b and c > 0 then ac > bc. Both sides of an inequality may be multiplied (or divided) by the same positive number without changing the sense of the inequality.

6. If a > b and c < 0 then ac < bc. That is, both sides of an inequality may be multiplied (or divided) by the same negative number but then the sense of the inequality is reversed.

7. If a > b and c > d then a + c > b + d. (Two inequalities having the same sense may be added termwise.)

8. If a > b and c < d then a – c > b – d

From one inequality it is possible to subtract termwise another inequality of the opposite sense, retaining the sense of the inequality from which the other was subtracted.

9. If a, b, c, d are positive numbers such that a > b and c > d then ac > bd, that is, two inequalities of the same sense in which both sides are positive can be multiplied termwise, the resulting inequality having the same sense as the multiplied inequalities.

10. If a and b are positive numbers where a > b, then aⁿ > bⁿ for any natural n.

11. If a and b are positive numbers where a > b then a^1/n > b^1/n for any natural n ≥ 2.

12. Two inequalities are said to be equivalent if the correctness of one of them implies the correctness of the other, and vice versa.

1. a² + b² ≥ 2ab (Equality for a = b)

2. |a + b | ≤ |a| + |b| (Equality reached if both a and b are of the same sign or if one of them is zero.) This can be generalised as \( |a_1 + a_2 + a_3 +...+a_n| \le |a_1| + |a_2| + |a_3| + ... + |a_n| \)

3. |a – b| ≥ |a| – |b|

4. ax² + bx + c ≥ 0 if a > 0 and D = b² – 4ac ≤ 0 . The equality is achieved only if D = 0 and x = –b/2a.

5. Arithmetic mean ≥ Geometric mean. That is, \( \frac{a+b}{2} \) ≥ ab

6. a/b + b/a ≥ 2 if a > 0 and b > 0 or if a < 0 and b < 0, that is, both a and b have the same sign.

7. a³ + b³ ≥ ab(a + b) if a > 0 and b > 0, the equality being obtained only when a = b.

8. a² + b² + c² ≥ ab + ac + bc

9. (a + b)(b + c)(a + c) ≥ 8 abc if a ≥ 0, b ≥ 0 and c ≥ 0, the equation being obtained when a = b = c

10. For any 4 numbers x₁ , x₂ , y₁ , y₂ satisfying the conditions x₁² + x₂² = 1 ; y₁² + y₂² = 1 ; the inequality \(|x_1y_1 + x_2y_2| \leq 1\) is true.

11. \( \frac{a}{b^{1/2}} + \frac{b}{a^{1/2}} \geq a^{1/2} + b^{1/2} \) where a ≥ 0 and b ≥ 0

12. If a + b = 2, then a⁴ + b⁴ ≥ 2

13. The inequality |x| ≤ a, means that –a ≤ x ≤ a for a > 0

14. 2ⁿ > n² for n ≥ 5

If a > b , then it is evident that a + c > b + c; a – c > b – c; ac > bc; a/c > b/c; that is, an inequality will still hold after each side has been increased, diminished, multiplied, or divided by the same positive quantity.

If a – c > b, By adding c to each side, a > b + c; which shows that in an inequality any term may be transposed from one side to the other if its sign is changed.

If a > b, then evidently b < a; that is, if the sides of an inequality be transposed, the sign of inequality must be reversed.

If a > b, then a – b is positive, and b – a is negative; that is, –a–(–b) is negative, and therefore –a < –b; hence, if the signs of all the terms of an inequality be changed, the sign of inequality must be reversed.

Again, if a > b, then –a < –b and, therefore, –ac < –bc; that is, if the sides of an inequality be multiplied by the same negative quantity, the sign of inequality must be reversed.

If a₁ > b₁ , a₂ > b₂ , a₃ > b₃ , .... , a_m > b_m, it is clear that a₁ + a₂ + a₃ + ... + a_m > b₁ + b₂ + b₃ + ... + b_m; and a₁ a₂ a₃… a_m > b₁ b₂ b₃ ... b_m.

If a > b, and if p, q are positive integers, then a^1/q > b^1/q and, therefore, a^p/q > b^p/q ; that is, aⁿ > bⁿ , where n is any positive quantity.

Further, 1/aⁿ < 1/bⁿ ; that is a^–n < b^–n

The square of every real quantity is positive, and therefore greater than zero. Thus (a – b)² is positive.

Let a and b be two positive quantities, S their sum and P their product.

Then from the identity 4ab = (a + b)² – (a – b)² we have 4P = S² – (a – b)², and S² = 4P + (a – b)²

Hence, if S is given, P is greatest when a = b; and if P is given, S is least when a = b;

That is, if the sum of two positive quantities is given, their product is greatest when they are equal; and if the product of two positive quantities is given, their sum is least when they are equal.

To Find the Greatest Value of a Product, the Sum of Whose Factors is Constant Let there be n factors a, b, c, ... , n, of a composite number and suppose that their sum is constant and equal to S.

Consider the product abc....n, and suppose that a and b are any two unequal factors. If we replace the two unequal factors a and b by the two equal factors (a + b)/2, and (a + b)/2, the product is increased while the sum remains unaltered.

Hence, so long as the product contains two unequal factors it can be increased altering the sum of the factors; therefore, the product is greatest when all the factors are equal.

In this case the value of each of the n factors is S/n, and the greatest value of the product is (S/n)ⁿ , or {(a + b + c + ... + n/n)}ⁿ

Let us define a number as a × b = c such that we restrict a + b = 100 (maximum).

Then, the maximum value of the product will be achieved if we take the value of a and b as 50 each. Thus 50 × 50 = 2500 will be the highest number achieved for the restriction a + b ≤ 100.

Further, you can also say that 50 × 50 > 51 × 49 > 52 × 48 > 53 × 47 > 54 × 46 > .... > 98 × 2 > 99 × 1

Thus if we have a larger multiplication as 4 × 6 × 7 × 8 this will always be less than 5 × 5 × 7 × 8. [Holds true only for positive numbers.]

Corollary If a, b, c ... , k, are unequal, {(a + b + c + ... + k)/n}ⁿ > abc...k; that is , (a + b + c +....+ k)/n > (abc...k)^1/n.

By an extension of the meaning of the arithmetic and geometric means this result is usually quoted as follows: The arithmetic mean of any number of positive quantities is greater than the geometric mean.

Definition of Solution of an Inequality The solution of an inequality is the value of an unknown for which this inequality reduces to a true numerical identity. That is, to solve an inequality means to find all the values of the variable for which the given inequality is true.

An inequality has no solution if there is no such value for which the given inequality is true. Equivalent Inequalities: Two inequalities are said to be equivalent if any solution of one is also a solution of the other and vice versa.

If both inequalities have no solution, then they are also regarded to be equivalent. To solve an inequality we use the basic properties of an inequality which have been illustrated above.

Notation of Ranges

1. Ranges where the ends are excluded If the value of x is denoted as (1, 2) it means 1 < x < 2 i.e. x is greater than 1 but smaller than 2.

Similarly, if we denote the range of values of x as –(7, –2)U(3, 21), this means that the value of x can be denoted as –7 < x < –2 and 3 < x < 21. This would mean that the inequality is satisfied between the two ranges and is not satisfied outside these two ranges.

Based on this notation write the ranges of x for the following representations: (1, + ∞) U (–∞, –7) (–∞, 0) U (4, +∞), (–∞, 50) U (–50, +∞)

2. Ranges where the Ends are Included [2, 5] means 2 ≤ x ≤ 5

3. Mixed ranges (3, 21] means 3 < x ≤ 21

Solving Linear Inequalities in one Unknown

A linear inequality is defined as an inequality of the form ax + b I 0 where the symbol ‘I’ represents any of the inequalities < , >, ≥ , ≤.

For instance if ax + b ≤ 0, then ax ≤ –b So x ≤ –b/a if a > 0 and x ≥ –b/a if a < 0

Example: Solve the inequality 2(x – 3) –1 > 3(x – 2) – 4(x + 1) so 2x – 7 > 3x – 6 – 4x – 4 so 3x > –3. Hence, x > –1

This can be represented in mathematical terms as (–1, +∞)

Example: Solve the inequality 2(x – 1) + 1 > 3 – (1 – 2x) so 2x – 1 > 2 + 2x so 0.x > 3 so This can never happen. Hence, no solution.

Example: Solve the inequality 2(x – 1) + 1 < 3 – (1 – 2x) Gives: 0.x < 3. This is true for all values of x

Example: Solve the inequality ax > a. This inequality has the parametre a that needs to be investigated further. If a > 0, then x > 1 If a < 0, then x < 1

Solving Quadratic Inequalities

A quadratic inequality is defined as an inequality of the form: ax² + bx + c I 0 ; where the symbol I represents any of the inequalities <, >, ≥, ≤.

For a quadratic expression of the form ax² + bx + c, (b² – 4ac) is defined as the discriminant of the expression and is often denoted as D. i.e. D = b² – 4ac

The following cases are possible for the value of the quadratic expression:

Case 1: If D < 0

1. If a < 0 then ax² + bx + c < 0 for all x

2. If a > 0 then ax² + bx + c > 0 for all x.

In other words, we can say that if D is negative then the values of the quadratic expression takes the same sign as the coefficient of x²

This can also be said as If D < 0 then all real values of x are solutions of the inequalities ax² + bx + c > 0 and ax² + bx + c ≥ 0 for a > 0 and have no solution in case a < 0.

Also, for D < 0, all real values of x are solutions of the inequalities ax² + bx + c < 0 and ax² + bx + c ≤ 0 if a < 0 and these inequalities will not give any solution for a > 0.

Case 2: D = 0 If the discriminant of a quadratic expression is equal to zero, then the value of the quadratic expression takes the same sign as that of the coefficient of x² (except when x = –b/2a at which point the value of the quadratic expression becomes 0).

We can also say the following for D = 0:

1. The inequality ax² + bx + c > 0 has as a solution any x = –(b/2a) if a > 0 and has no solution if a < 0.

2. The inequality ax² + bx + c < 0 has as a solution any x = –(b/2a) if a < 0 and has no solution if a > 0.

3. The inequality ax² + bx + c ≥ 0 has as a solution any x if a > 0 and has a unique solution x = –b/2a if a < 0.

4. The inequality ax² + bx + c ≤ 0 has as a solution any x if a < 0 and has a unique solution x = –b/2a for a > 0.

Case 3: D > 0 If x₁ and x₂ are the roots of the quadratic expression then it can be said that:

1. For a > 0, ax² + bx + c is positive for all values of x outside the interval [x₁, x₂] and is negative for all values of x within the interval (x₁, x₂). Besides for values of x = x₁ or x = x₂ , the value of the quadratic expression becomes zero (By definition of the root).

2. For a < 0, ax² + bx + c is negative for all values of x outside the interval [x₁, x₂] and is positive for all values of x within the interval (x₁, x₂). Besides for values of x = x₁ or x = x₂ , the value of the quadratic expression becomes zero (By definition of the root).

Here are a few examples illustrating how quadratic inequalities are solved. Solve the following inequalities. Example 1: x² – 5x + 6 > 0

Solution: (a) The discriminant D = 25 – 4 × 6 > 0 and a is positive (+1); the roots of the quadratic expression are real and distinct: x₁ = 2 and x₂ = 3.

By the property of quadratic inequalities, we get that the expression is positive outside the interval [2, 3]. Hence, the solution is x < 2 and x > 3. We can also see it as x² – 5x + 6 = (x – 2) (x – 3) and the given inequality takes the form (x – 2) (x – 3) > 0.

The solutions of the inequality are the numbers x < 2 (when both factors are negative and their product is positive) and also the numbers x > 3 (when both factors are positive and, hence, their product is also positive).

Answer: x < 2 and x > 3.

Example 2: 2x² + x + 1 ≥ 0

Solution: The discriminant D = 1 – 4 * (– 2) = 9 > 0; the roots of the quadratic expression are real and distinct:

\(x_{1,2} = \frac{-1 \pm \sqrt{9}}{2.(-2)} = \frac{-1\pm(-3)}{-4}\)

hence, x₁ = – 1/2 and x₂ = 1, and consequently, –2x² + x + 1 = –2(x + 1/2) × (x – 1).

We have –2(x + 1/2) (x – 1) ≥ 0 or (x + 1/2) (x – 1) ≤ 0

(When dividing both sides of an inequality by a negative number, the sense of the inequality is reversed).

The inequality is satisfied by all numbers from the interval [–1/2, 1]

Please note that this can also be concluded from the property of quadratic expressions when D > 0 and a is negative.

Answer: –1/2 ≤ x ≤ 1.

Example 3: 2x² + x – 1 < 0

Solution: D = 1 – 4 * (–2) * (–1) < 0, the coefficient of x² is negative. By the property of the quadratic expression when D < 0 and a is negative –2x² + x – 1 attains only negative values.

Answer: x can take any value.

Example 4: 3x² – 4x + 5 < 0

Solution: D = 16 – 4 × 3 × 5 < 0, the coefficient of x² is positive.

The quadratic expression 3x² – 4x + 5 takes on only positive values.

Answer: There is no solution.

Example 5: 4x² + 4x + 1 > 0.

Solution: D = 16 – 4 × 4 = 0. The quadratic expression 4x² + 4x + 1 is the square (2x + 1)² , and the given inequality takes the form (2x + 1)² > 0.

It follows that all real numbers x, except for x = –1/2, are solutions of the inequality.

Answer: x = –1/2.

Example 6: Solve the inequality (a – 2)x² – x – 1 ≥ 0

Here, the value of the determinant D = 1 – 4(–1)(a – 2) = 1 + 4(a – 2) = 4a – 7

There can then be three cases:

Case 1: D < 0 so a < 7/4

Then the coefficient of x² so a – 2 is negative.

Hence, the inequality has no solution.

Case 2: D = 0 a = 7/4. Put a = 7/4 in the expression and then the inequality becomes –(x – 2)² ≥ 0. This can only happen when x = 2.

Case 3: D > 0 Then a > 7/4 and a = 2, then we find the roots x₁ and x₂ of the quadratic expression:

\(x_1 = \frac{1 + \sqrt{4a-7}}{2(a-2)} , x_2 = \frac{1 + \sqrt{4a-7}}{2(a-2)} \)

Using the property of quadratic expression’s values for D > 0 we get If a – 2 < 0, the quadratic expression takes negative values outside the interval [x₁, x₂].

Hence, it will take positive values inside the interval (x₁, x₂).

If a – 2 > 0, the quadratic expression takes positive values outside the interval [x₁, x₂] and becomes zero for x₁ and x₂.

If a – 2 = 0, then we get a straight linear equation. –x – 1 ≥ 0 so x ≤ – 1.

System of Inequalities in One Unknown

Let there be given several inequalities in one unknown. If it is required to find the number that will be the solution of all the given equalities, then the set of these inequalities is called a system of inequalities. The solution of a system of inequalities in one unknown is defined as the value of the unknown for which all the in-equalities of the system reduce to true numerical inequalities.

To solve a system of inequalities means to find all the solutions of the system or to establish that there is none.

Two systems of inequalities are said to be equivalent if any solution of one of them is a solution of the other, and vice versa. If both the systems of inequalities have no solution, then they are also regarded to be equivalent.

Example 1: Solve the system of inequalities: 3x – 4 < 8x + 6 2x – 1 > 5x – 4 11x – 9 ≤ 15x + 3

Solution: We solve the first inequality: 3x – 4 < 8x + 6 –5x < 10 x > –2 It is fulfilled for x > –2. Then we solve the second inequality 2x – 1 > 5x – 4 –3x > – 3 x < 1 It is fulfilled for x < 1.

And, finally, we solve the third inequality: 11x – 9 ≤ 15x + 3 –4x ≤ 12 x ≥ – 3

It is fulfilled for x ≥ – 3. All the given inequalities are true for – 2 < x < 1.

Answer: – 2 < x < 1.

Example 2: Solve the inequality < 1

We have –1 < 0 ≤ < 0 This means that the fraction above has to be negative. A fraction is negative only when the numerator and the denominator have opposite signs. Hence, the above inequality is equivalent to the following set of 2 inequalities: x – 2 > 0 and x – 2 < 0 and x + 1 < 0 x + 1 > 0 From the first system of inequalities, we get x > 2 or x < –1. This cannot happen simultaneously since these are inconsistent. From the second system of inequalities we get x < 2 or x > –1 i.e –1 < x < 2 Inequalities Containing a Modulus Result: | x | ≤ a, where a > 0 means the same as the double inequality –a ≤ x ≤ a This result is used in solving inequalities containing a modulus.

Example 1: | 2x – 3 | ≤ 5

This is equivalent to –5 ≤ 2x – 3 ≤ 5 i.e. 2x – 3 ≥ –5 and 2x – 3 ≤ 5 2x ≥ –2 x ≤ 4 x ≥ –1

The solution is

–1 ≤ x ≤ 4

Example 2: | 1 – x | > 3

| 1 – x | = | x – 1 | Hence, | x – 1 | > 3 so x – 1 > 3 i.e x > 4 or x – 1 < –3 or x < –2 Answer: x > 4 or x < –2.

|x – 2| ≤ 2x² – 9x + 9

x > (4 – \( \sqrt{2} \) )/2

x < (5 + \( \sqrt{3} \))/2

Both (a) and (b)

None of these

Explanation :
```
at (b) inequality is satisfied
```

|x – 6| < x² – 5x + 9

x < 1

x > 3

1 < x < 3

Both (a) and (b)

Explanation :

at values 4 and above inequality is satisfied

|x – 6| > x² – 5x + 9

1 ≤ x < 3

1 < x < 3

2 < x < 5

–3 < x < 1

Explanation :

At x = 2, inequality is satisfied.
At x = 0, inequality is not satisfied.
At x = 1, inequality is not satisfied but LHS = RHS.
At x = 3, inequality is not satisfied but LHS = RHS.
Thus, option (b) is correct.

x² – |5x – 3| – x < 2

x > 3 + 2\( \sqrt{2} \)

x < 3 + 2\( \sqrt{2} \)

x > –5

–5 < x < 3 + 2\( \sqrt{2} \)

Explanation :

At x = 0, inequality is satisfied, option (a) rejected.
At x = 10, inequality is not satisfied, option (c) rejected.
At x = –5, LHS = RHS.
Also at x = 5, inequality is satisfied and at x = 6, inequality is not satisfied.
Thus, option (d) is correct.

x² – 7x + 12 < |x – 4|

x < 2

x > 4

2 < x < 4

2 ≤ x ≤ 4

Explanation :

At x = 0, inequality is not satisfied, option (a) is rejected.
At x = 5, inequality is not satisfied, option (b) is rejected.
At x = 2 inequality is not satisfied.
Options (d) are rejected.
Option (c) is correct.

|x² – 3x| + x – 2 < 0

(1 - \( \sqrt{3} \)) < x < (2 + \( \sqrt{3} \))

0 < x < 5

(1 - \( \sqrt{3} \), 2 - \( \sqrt{3} \))

1 < x < 4

Explanation :

The options need to be converted to approximate values before you judge the answer. At x = 0,
inequality is satisfied.
Thus, option (a) is rejected.
Option (c) is correct.

|x² – 2x – 3| < 3x – 3

1 < x < 3

–2 < x < 5

x > 5

2 < x < 5

Explanation :

|x² – 2x| < x

1 < x < 3

–1 < x < 3

0 < x < 4

x > 3

Explanation :

At x = 1 and x = 3 LHS = RHS.
At x = 2 inequality is satisfied.
At x = 0.1 inequality is not satisfied.
At x = 2.9 inequality is satisfied.
At x = 3.1 inequality is not satisfied.
Thus, option (a) is correct.

|x² – 5x| < 6

–1 < x < 2

3 < x < 6

Both (a) and (b)

–1 < x < 6

Explanation :

|x² + x| – 5 < 0

x < 0

x > 0

All values of x

None of these

Explanation :

At x = 0 inequality is satisfied.
Thus, options (a), (b), and (d) are rejected.
Option (c) is correct.

|x² – 4x| < 5

–1 ≤ x ≤ 5

1 ≤ x ≤ 5

–1 ≤ x ≤ 1

–1 < x < 5

Explanation :

At x = 0 inequality is satisfied, option (b) is rejected.
At x = 2, inequality is satisfied, option (c) is rejected.
At x = 5, LHS = RHS.
At x = –1, LHS = RHS.
Thus, option (d) is correct.

2 – x – x² ≥ 0

–2 ≤ x ≤ 1

–2 < x < 1

x < –2

x > 1

Explanation :

At x = 0, inequality is satisfied.
Thus, options, (c) and (d) are rejected.
At x = 1, inequality is satisfied
Hence, we choose option (a)

x² – 14x – 15 > 0

x < –1

15 < x

Both (a) and (b)

-1 < x < 15

Explanation :

At x = 0 inequality is not satisfied. Thus option (d) is rejected.
x = –1 and x = 15 are the roots of the quadratic equation. Thus, option (c) is correct.

x² – 3x + 5 > 0

x > 0

x < 0

Both (a) and (b)

–∞ < x < ∞

Explanation :

The given quadratic equation has imaginary roots and is hence always positive.
Thus, option (d) is correct

3x² – 7x + 6 < 0

0.66 < x < 3

–0.66 < x < 3

–1 < x < 3

None of these

Explanation :

At x = 0, inequality is not satisfied.
Hence, options (b), (c) and (d) are rejected. At x = 2, inequality is not satisfied. Hence, option (a)
is rejected.
Thus, option (d) is correct.

3x² – 7x – 6 < 0

–0.66 < x < 3

x < – 0.66 or x > 3

3 < x < 7

–2 < x < 2

Explanation :

At x = 0, inequality is satisfied. Hence, options (b) and (c) are rejected. x = 3 gives LHS = RHS.
and x = – 0.66 also does the same. Hence. roots of the equation are 3 and – 0.66.
Thus, option (a) is correc

3x² – 7x + 4 ≤ 0

x > 0

x < 0

All x

None of these

Explanation :

At x = 0, inequality is not satisfied. Thus, option (c) is rejected. Also x = 0 is not a solution of the
equation. Since, this is a continuous function, the solution cannot start from 0. Thus options (a) and
(b) are not right. Further, we see that the given function is quadratic with real roots.

Equations in one variable : An equation is any expression in the form f(x) = 0; the type of equation we are talking about depends on the expression that is represented by f(x). The expression f(x) can be linear, quadratic, cubic or might have a higher power and accordingly the equation can be referred to as linear equations, quadratic equations, cubic equations, etc.

Linear Equations : 2x + 4 = 0; we have the expression for f(x) as a linear expression in x. Consequently, the equation 2x + 4 = 0 would be charaterised as a linear equation.

This equation has exactly 1 root (solution) and can be seen by solving 2x + 4 = 0 Æ x = –2 which is the root of the equation.

Note that the root or solution of the equation is the value of ‘x’ which would make the LHS of the equation equal the RHS of the equation. In other words, the equation is satisfied when the value of x becomes equal to the root of the equation.

The linear function f(x) when drawn would give us a straight line and this line would be intersecting with the x-axis at the point where the value of x equals the root (solution) of the equation

Quadratic Equations : An equation of the form: 2x² – 5x + 4 = 0; we have the expression for f (x) as a quadratic expression (1)in x. Consequently, the equation 2x² – 5x + 4 = 0 would be charaterised as a quadratic equation. This equation has exactly 2 roots (solutions) and leads to the following cases with respect to whether these roots are real/imaginary or equal/unequal.

Case 1: Both the roots are real and equal;

Case 2: Both the roots are real and unequal;

Case 3: Both the roots are imaginary.

The graph of a quadratic function is always U shaped and would just touch the X-Axis in the first case above, would cut the X-Axis twice in the second case above and would not touch the X-Axis at all in the third case above.

Note that the roots or solutions of the equation are the values of ‘x’ which would make the LHS of the equation equal the RHS of the equation. In other words, the equation is satisfied when the value of x becomes equal to the root of the equation.

An equation of the form: x³ + 2x² – 5x + 4 = 0 where the expression f(x) is a cubic expression in x. Consequently, the expression would have three roots or solutions. Depending on whether the roots are real or imaginary we can have the following two cases in this situation

Case 1: All three roots are real; (Graph might touch/cut the x-axis once, twice or thrice.) In this case depending on the equality or inequality of the roots we might have the following cases:

Case (i) All three roots are equal; (The graph of the function would intersect the X-axis only once as all the three roots of the equation coincide.)

Case (ii) Two roots are equal and one root is distinct; (In this case the graph cuts the X-axis at one point and touches the X-Axis at another point where the other two roots coincide.)

Case (iii) All three roots are distinct from each other. (In this case the graph of the function cuts the x-axis at three distinct points.)

Case 2: One root is real and two roots are imaginary. (Graph would cut the X-axis only once.) The shapes of the graph that a cubic function can take has already been discussed as a part of the discussion on the Back to School write up of this block.

Note: For a cubic equation ax³ + bx² + cx + d = 0 with roots as l, m and n:

The product of its three roots viz: lmn = –d/a;

The sum of its three roots viz: l + m + n = –b/a

The pairwise sum of its roots taken two at a time viz: lm + ln + mn = c/a.

An equation of the form ax² + bx + c = 0 where a, b and c are all real and a is not equal to 0, is a quadratic equation.

Then, D = (b² – 4ac) is the discriminant of the quadratic equation.

If D < 0 (i.e. the discriminant is negative) then the equation has no real roots.

If D > 0, (i.e. the discriminant is positive) then the equation has two distinct roots, namely, x1 = (–b + \( \sqrt{D} \))/2a, and x2 = (–b – \( \sqrt{D} \))/2a and then ax² + bx + c = a (x – x₁) (x – x₂) ... form (2)

If D = 0, then the quadratic equation has equal roots given by x₁ = x₂ = –b/2a and then ax² + bx + c = a (x – x₁)² ... form (3)

To represent the quadratic ax² + bx + c in form (2) or (3) is to expand it into linear factors.

Properties of Quadratic Equations and Their Roots

(i) If D is a perfect square then the roots are rational and in case it is not a perfect square then the roots are irrational.

(ii) In the case of imaginary roots (D < 0) and if p + iq is one root of the quadratic equation, then the other must be the conjugate p – iq and vice versa (where p and q are real and i = \( \sqrt{-1} \))

(iii) If p + \( \sqrt{q} \) is one root of a quadratic equation, then the other must be the conjugate p – \( \sqrt{q} \) and vice versa. (where p is rational and \( \sqrt{q} \) is a surd).

(iv) If a = 1, b, c ∈ I and the roots are rational numbers, then the root must be an integer.

(v) If a quadratic equation in x has more than two roots, then it is an identity in x.

The Sign of a Quadratic Expression

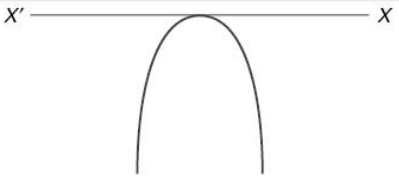
Let f(x) = y = ax² + bx + c where a, b, c are real and a = 0, then y = f(x) represents a parabola whose axis is parallel to y-axis. For some values of x, f (x) may be positive, negative or zero. Also, if a > 0, the parabola opens upwards and for a < 0, the parabola opens downwards.

This gives the following cases:

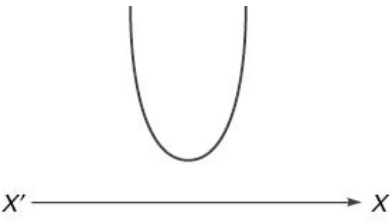
(i) a > 0 and D < 0 (The roots are imaginary) The function f(x) will always be positive for all real values of x. So f(x) > 0 ; x ∈ R. Naturally the graph as shown in the figure does not cut the X-Axis.

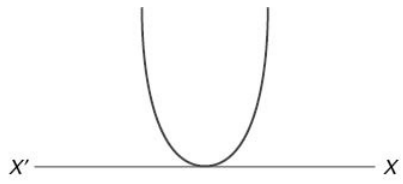
(ii) When a > 0 and D = 0 (The roots are real and identical.) f (x) will be positive for all values of x except at the vertex where f(x) = 0.

So f(x) ≥ 0 " x ∈ R. Naturally, the graph touches the X-Axis once.

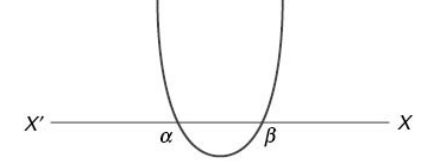
(iii) When a > 0 and D > 0 (The roots are real and distinct)

Let f(x) = 0 have two real roots a and b (a < b) then f(x) will be positive for all real values of x which are lower than a or higher than b; f(x) will be equal to zero when x is equal to either of a or b.

When x lies between a and b then f(x) will be negative. Mathematically, this can be represented as f(x) > 0 " x ∈ (–∞, a) and (b, ∞) and f(x) < 0 ; x ∈ (a, b) (Naturally the graph cuts the X axis twice)

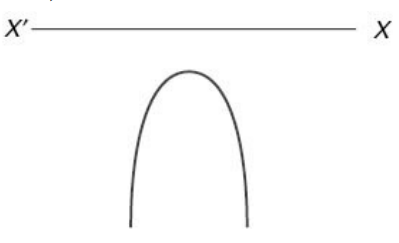
(iv) When a < 0 and D < 0 (Roots are imaginary) f(x) is negative for all values of x. Mathematically, we can write f(x) < 0 ; x ∈ R. (The graph will not cut or touch the X axis.)

(v) When a < 0 and D = 0 (Roots are real and equal) f(x) is negative for all values of x except at the vertex where f(x) = 0. i.e. f(x) ≤ 0 " x ∈ R (The graph touches the X axis once.)

(vi) When a < 0 and D > 0 Let f(x) = 0 have two roots a and b (a < b) then f(x) will be negative for all real values of x that are lower than a or higher than b. f(x) will be equal to zero when x is equal to either of a or b. The graph cuts the X axis twice.

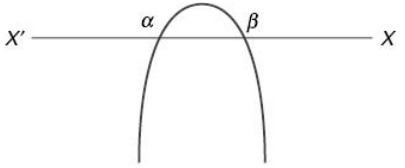
When x lies between a and b then f(x) will be positive.

Mathematically, this can be written as f(x) < 0 ; x ∈ (–∞, a) && (b, ∞) and f(x) > 0 ; x ∈ (a, b).

Sum of the roots of a quadratic Equation = –b/a.

Product of the roots of a quadratic equation = c/a

Equations in more than one Variable : Sometimes, an equation might contain not just one variable but more than one variable. In the context of an aptitude examination like the CAT, multiple variable equations may be limited to two or three variables.

Consider this question from an old CAT examination which required the student to understand the interrelationship between the values of x and y.

The question went as follows : 4x – 17y = 1 where x and y are integers with x,y > 0 and x, y < 1000. How many pairs of values of (x, y) exist such that the equation is satisfied?

In order to solve this equation, you need to consider the fact that 4x in this equation should be looked upon as a multiple of 4 while 17y should be looked upon as a multiple of 17.

A scan of values which exist such that a multiple of 4 is 1 more than a multiple of 17 starts from 52 – 51 = 1, in which case the value of x = 13 and y = 3. This represents the first set of values for (x, y) that satisfies the equation.

The next pair of values in this case would happen if you increase x from 13 to 30 (increase by 17 which is the coefficient of y); at the same time increase y from 3 to 7 (increase by 4 which is the coefficient of x).

The effect this has on 4x is to increase it by 68 while 17y would also increase by 68 keeping the value of 4x exactly 1 more than 17y. In other words, at x = 30 and y = 7 the equation would give us 120–119 = 1.

Going further, you should realise that the same increases need to be repeated to again identify the pair of x, y values. (x = 47 and y = 11 gives us 188–187 = 1)

Once, you realise this, the next part of the visualisation in solving this question has to be on creating the series of values which would give us our desired outcomes everytime. This series can be viewed as

(13,3); (30,7); (47,11); (64,15) ... and the series would basically be two arithmetic progressions running parallel to each other (viz: 13, 30, 47, 64, 81, ... ) and (3, 7, 11, 15, 19, ...) and obviously the number of such pairs would depend on the number of terms in the first of these arithmetic progressions (since that AP would cross the upper limit of 1000 first).

You would need to identify the last term of the series below 1000. The series can be visualised as 13, 30, 47, 64, ... 999 and the number of terms in this series is 986/17 + 1 = 59 terms. [Refer to the chapter on arithmetic Progressions for developing the thinking that helps us do these last two steps.]

If [x] denotes the greatest integer ≤ x, then \( \frac{1}{3} + [\frac{1}{3} + \frac{1}{99}] + [\frac{1}{3} + \frac{2}{99}] .. + [\frac{1}{3} + \frac{198}{99}] \)

132

165

Explanation :
When the value of the sum of the terms inside the function is less than 1, the value of its greatest integer function would be 0. In the above sequence of values, the value inside the bracket would become equal to 1 or more from the value \( [\frac{1}{3} + \frac{66}{99}] \). Further, this value would remain between 1 to 2 till the term \( [\frac{1}{3} + \frac{164}{99}] \). There would be 99 terms each with a value of 1 between 66/99 to 164/99. Hence, this part of the expression would each yield a value of 1 giving us: \( [\frac{1}{3} + \frac{66}{99}] + [\frac{1}{3} + \frac{67}{99}] + ... + [\frac{1}{3} + \frac{164}{99}]\) = 99 Further, from \( [\frac{1}{3} + \frac{166}{99}] + [\frac{1}{3} + \frac{167}{99}] + ... + [\frac{1}{3} + \frac{198}{99}]\) = 2 × 33 = 66 This gives us a total value of 99 + 66 = 165 which means that Option (d) is the correct answer

If 13x + 17y = 643, where x and y are natural numbers, what is the value of two times the product of x and y?

744

844

924

884

Explanation :

The solution of this question depends on your visualisation of the multiples of 13 and 17 which
would satisfy this equation. (Note: your reaction to 13x should be to look at it as a multiple of 13 while
17y should be looked at as a multiple of 17). A scan of multiples of 13 and 17 gives us the solution at 286
+ 357 which would mean 13 × 22 and 17 × 21 giving us x as 22 and y as 21. The value of 2xy would be 2
× 22 × 21 = 2 × 462 = 924.

The product of the roots of the equation mx² + 6x + (2m – 1) = 0 is – 1. Then m is

1/3

-1

-1/3

Explanation :
```
We have (2m – 1)/m = –1 fi m = 1/3
```

Solve the system of equations 1/x + 1/y = 3/2; 1/x² + 1/y² = 5/4

(1, 2)

(2, 1)

both

none

Explanation :

Let 1/x = u and 1/y = v. We then obtain
u + v = 3/2
u² + v² = 5/4
From the first equation, we find v = (3/2) – u and substitute this expression into the second equation
u² + ((3/2) – u)² = 5/4 or 2u² – 3u + 1 = 0
when u₁ = 1 and u₂ = 1/2; consequently, v₁ = 1/2 and v₂ = 1. Therefore, x₁ = 1,
y₁ = 2 and x₂ = 2, y₂ = 1
Answer: (1, 2) and (2, 1).

What is the condition for one root of the quadratic equation ax² + bx + c = 0 to be twice the other?

b² = 4ac

2b² = 9ac

c² = 4a + b²

c² = 9a – b²

Explanation :

Alternative: Assume any equation having two roots as 2 and 4 or any equation having two roots one of
which is twice the other.
When roots are 2 and 4, then equation will be (x – 2) (x – 4) = x² – 6x + 8 = 0.
Now, check the options one by one and you will find only (b) as a suitable option.

If the roots of the equation x² – bx + c = 0 differ by 2, then which of the following is true?

c² = 4(c + 1)

b² = 4c + 4

c² = b + 4

b² = 4(c + 2)

Explanation :

Let the roots be a and a + 2.
Then a + a + 2 = b fi a = (b – 2)/2
and a(a + 2) = c fi a² + 2a = c
Putting the value of a from (1) in (2).
((b – 2)/2)² + 2(b – 2)/2) = c
fi (b² + 4 – 4b)/4 + b – 2 = c
fi b² + 4 – 8 = 4c
fi b² = 4c + 4
\ Option (b) is the correct answer.

The number of roots of the equation x – 2/(x-1) = 1 – 2/(x-1) is

infinite

Explanation :

The equation gives x = 1.
But x = 1 is not admissible because it gives x – 1 = 0 which, in turn, makes the whole expression like this:
x–2/0 = 1–2/0. But 2/0 gives the value as infinity so, no solution is possible.

If the roots of the equation a(b – c)x² + b(c – a)x + c(a – b) = 0 are equal, then a, b, c are in

Cannot be determined

Explanation :

n Since roots of the equation a (b – c)x² + b (c – a)x + c (a – b) = 0 are equal
fi b²(c – a)² – 4ac(b – c)(a – b) = 0
fi b²(c + a)² – 4abc(a + c) + 4a²c² = 0
fi [b(c + a) – 2ac]² = 0 fi b(c + a) – 2ac = 0
fi b = (2ac)/(a +c) fi a, b, c, are in HP

If p and q are the roots of the equation x² + px + q = 0

p = 1

p = 1 or 0 or –1/2

p = –2

p = –2 or 0

Explanation :

 Since p and q are roots of the equation x² + px + q = 0,
p² + p² + q = 0 and q² + pq + q = 0
fi 2p² + q = 0 and q(q + p + 1) = 0
fi 2p² + q = 0 and q = 0 or q = –p –1
When we use, q = 0 and 2p² + q = 0
we get p = 0.
or when we use q = –p – 1 and 2p² + q = 0
we get 2p² – p – 1 = 0 so which gives us
p = 1 or p = –1/2
Hence, there can be three values for p
i.e. p = 1, p = 0, or p = –1/2

One of the two students, while solving a quadratic equation in x, copied the constant term incorrectly and got the roots 3 and 2. The other copied the constant term and coefficient of x 2 correctly as –6 and 1 respectively. The correct roots are

3, –2

–3, 2

– 6, –1

6, –1

Explanation :

Let a, b be the roots of the equation. Then a + b = 5 and ab = –6. So, the equation is x
2 – 5x – 6
= 0. The roots of the equation are 6 and –1.

Find the value of \( \sqrt{6 + \sqrt{6 + \sqrt{6 + ..}}} \)

3.5

2.5

Explanation :
Let y = \( \sqrt{6 + \sqrt{6 + \sqrt{6 + ..}}} \) Then, y = \( \sqrt{6 +y} \) or y² – y – 6 = 0 or, (y + 2) (y – 3) = 0 so y = –2, 3 y = –2 is not admissible Hencey = 3

Find the maximum value of the expression \( \frac{1}{x^2 + 5x + 10} \)

15/2

4/15

1/3

Explanation :

For the given expression to be a maximum, the denominator should be minimized. (Since, the
function in the denominator has imaginary roots and is always positive). x
2 + 5x + 10 will be
minimized at x = –2.5 and its minimum values at x = –2.5 is 3.75.
Hence, required answer = 1/3.75 = 4/15.

Explanation :

If a = \( \sqrt{7 + 4\sqrt{3}} \), what will be the value of (a + 1/a)?

Explanation :

The approximate value of a = √(13.92) = 3.6 (approx).
a + 1/a = 3.6 + 1/3.6 is closest to 4

Find the value of the expression \( \sqrt{x + \sqrt{x + \sqrt{x + ...}}} \)

1/2[2 \( \sqrt{(2x-1)} \) + 1]

1/2[ \( \sqrt{(4x+1)} \) + 1]

1/2[2 \( \sqrt{(2x-1)} \) - 1]

1/2[ \( \sqrt{(4x-1)} \) - 1]

Explanation :
y = \( \sqrt{x + \sqrt{x + \sqrt{x + ...}}} \) assume y = \( \sqrt{x + \sqrt{x + \sqrt{x + ...}}} \) so y = \( \sqrt{x + y} \) y² = x + y y² – y – x = 0 Solving quadratically, we have option (b) as the root of this equation.

If a and b are the roots of the Quadratic equation 5y² – 7y + 1 = 0 then find the value of 1/α + 1/β

7/25

-7

-7/25

Explanation :

1/a + 1/b = (a + b)/ab
= (7/5)/(1/5) = 7.

Two numbers a and b are such that the quadratic equation ax² + 3x + 2b = 0 has – 6 as the sum and the product of the roots. Find a + b.

-1

-2

Explanation :

–3/a = –6 fi a = ½,
2b/a = –6 and a = ½
Gives us b = –1.5.
a + b = –1.

For what value of c the quadratic equation x² – (c + 6) x + 2(2c – 1) = 0 has sum of the roots as half of their product?

-4

Explanation :

(c + 6) = 1/2 × 2(2c – 1) fi c + 6 = 2c – 1 fi c = 7

If the roots of the equation (a² + b²)x² – 2(ac + bd)x + (c² + d²) = 0 are equal then which of the following is true?

ab = cd

ad = bc

ad = \( \sqrt{bc} \)

ab = \( \sqrt{cd} \)

Explanation :

Solve this by assuming each option to be true and then check whether the given expression has
equal roots for the option under check.
Thus, if we check for option (b).
ad = bc.
We assume a = 6, d = 4 b = 12 c = 2 (any set of values that satisfies ad = bc).
Then (a² + b²) x² – 2(ac + bc) x + (c² + d²) = 0
180 x² – 120 x + 20 = 0.
We can see that this has equal roots. Thus, option (b) is a possible answer. The same way if we
check for a, c and d we see that none of them gives us equal roots and can be rejected.

If equation x² + bx + 12 = 0 gives 2 as its one of the roots and x² + bx + q = 0 gives equal roots then the value of b is

49/4

-8

25/2

Explanation :

x² + bx + 12 = 0 has 2 as a root.
Thus, b = –8.

If f(x) = (x + 2) and g(x) = (4x + 5), and h(x) is defined as h(x) = f(x) * g(x), then sum of roots of h (x) will be

3/4

13/4

-13/4

-3/4

Explanation :

h (x) = 4x² + 13x + 10.
Sum of roots – 13/4.

If the roots of equation x² + bx + c = 0 differ by 2, then which of the following is true?

a²c² = 4(1 + c)

4b + c = 1

c² = 4 + b

b² = 4 (c + 1)

Explanation :

To solve this take any expression whose roots differ by 2.
Thus, (x – 3) (x – 5) = 0
x² – 8x + 15 = 0
In this case, a = 1, b = –8 and c = 15.
We can see that b² = 4(c + 1).

The expression a² + ab + b² is _________for a < 0, b < 0

≥ 0

< 0

> 0

= 0

Explanation :

For a, b negative the given expression will always be positive since, a², b² and ab are all
positive.

For the equation 2^{a + 3} = 4^{a + 2} – 48, the value of a will be

-3/2

-3

-2

Explanation :

Solve through options. LHS = RHS for a = 1.

If the product of roots of the equation x² – 3 (2a + 4) x + a² + 18a + 81 = 0 is unity, then a can take the values as

3, – 6

10, – 8

–10, –8

–10, – 6

Explanation :

The product of the roots is given by: (a² + 18a + 81)/1.
Since product is unity we get: a² + 18a + 81 = 1
Thus, a² + 18a + 80 = 0
Solving, we get: a = –10 and a = – 8.

Find the minimum value of the expression (p +1/p); p > 0.

Depends upon the value of p

Explanation :

The minimum value of (p + 1/p) is at p = 1. The value is 2.

Find the maximum value of the expression (x² + 8x + 20).

None of these

Explanation :
```
Has no maximum
```

Find the number of solutions of a³ + 2^a+1 = a⁴ , given that n is a natural number less than 100

Explanation :

In order to think of this situation, you need to think of the fact that “the cube of a number + a power
of two” (LHS of the equation) should add up to the fourth power of the same number.
The only in which situation this happens is for 8 + 8 = 16 where a = 2 giving us 2³ + 2³ = 2⁴.
Hence, Option (b) is the correct answer.

If 9^{a – 2} ÷ 3^{a + 4} = 81^{a – 11} , then find the value of 3^{a – 8} + 3^{a – 6}

972

2916

810

2268

Explanation :

Simplifying the equation 9^{a – 2} 3^{a + 4} = 81^{a – 11} 
we will get: 3^{2a – 4} ÷ 3^{a + 4} = 3^{4a – 44}
. This gives us:
2a–4 – a – 4 = 4a–44 so a–8 = 4a–44 so 3a = 36 so a = 12.
Hence, we have to evaluate the value of 3⁴ + 3⁶ = 81 + 729 = 810. Option (c) is correct.

The expression x² + kx + 9 becomes positive for what values of k (given that x is real)?

k < 6

k > 6

|k| < 6

|k| ≤ 6

Explanation :

The roots should be imaginary for the expression to be positive
i.e. k² – 36 < 0
thus – 6 < k < 6 or |k| < 6.

If a and b are roots of the equation x² + x – 7 = 0 then Find a² + b²

Explanation :

(a² + b²) = (a + b)² – 2ab
= (–1)
2 – 2 × (–7) = 15.

If a and b are roots of the equation x² + x – 7 = 0 then Find a 3 + b 3

-22

Explanation :

(a³ + b³) = ( + b)² – 3 × b(a + b)= (–1)
3 – 3 × (–7) (–1) = –1 – 21 = –22

If a and b are roots of the equation x² + x – 7 = 0 then For what values of c in the equation 2x² – (c³ + 8c – 1)x + c² – 4c = 0 the roots of the equation would be opposite in signs?

c ⊆ (0, 4)

c ⊆ (– 4, 0)

c ⊆ (0, 3)

c ⊆ (– 4, 4)

Explanation :

For the roots to be opposite in sign, the product should be negative.
(c2 – 4x)/2 < 0 so 0 < c < 4.

If a and b are roots of the equation x² + x – 7 = 0 then The set of real values of x for which the expression x 2 – 9x + 20 is negative is represented by

4 < x <= 5

4 < x < 5

x < 4 or x > 5

–4 < x < 5

Explanation :

The roots of the equation x² – 9x + 20 = 0 are 4 and 5. The expression would be negative for 4 < x
< 5.

Find all the values of b for which the equation x² – bx + 1 = 0 does not possess real roots.

–1 < b < 1

0 < b < 2

–2 < b < 2

–1.9 < b < 1.9

Explanation :
```
b² – 4 < 0 so – 2 < b < 2
```

If x² + ax + b leaves the same remainder 5 when divided by x – 1 or x + 1 then the values of a and b are respectively

0 and 4

3 and 0

0 and 3

4 and 0

Explanation :

Remainder when x² + ax + b is divided by x – 1 is got by putting x = 1 in the expression. Thus, we
get.
a + b + 1 = 5 and
b – a + 1 = 5
so b = 4 and a = 0

Chapter 14 D: Inequalities

Facts and Formulae

Certain Important Inequalities

Some Important Results

Additional notes

Solved Question Papers

THEORY OF EQUATIONS

Cubic Equations

THEORY OF QUADRATIC EQUATIONS

Solved Question Papers