NUMBER THEORY - Aptitude

Chapter 2: NUMBER THEORY

Introduction

Highest common factor :

If there are three numbers like 10, 20, 30 and there exists numbers that can divide them to give remainder 0 viz. 5, 10. Then the lowest of those numbers is the HCF viz. 5

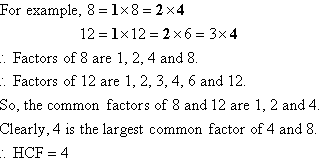
Least Common multiple:

If we take 4,6 as two numbers then both of them divide 12, 24, 36 etc fully giving remainder 0 so the lowest such number common to both is the LCM which in this case is 12.

Method 1:

Method 2:

Questions:

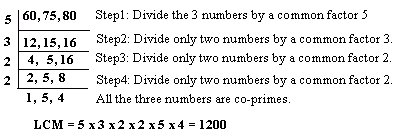
Q. What is the least number of cans needs for a vendor who has 21 L of Milk 'a' , 42 L of milk 'b' and 63L of Milk 'c'. If all cans should have same number of milk and he should need least number of cans.

Ans: Find HCF of 21, 42, 63 which is 21. So total cans are 6 i.e. 1 for milk 'a' , 2 for milk 'b' and 3 for milk 'c'.

Q. If the HCF and LCM of two numbers is 18, 180 and one of the number is 36. Then the second number is.

Ans. HCF * LCM = a * but HCF = 18, LCM = 180 and a= 36 so substituting we get b = 90.

Formulae of HCF and LCM

If a,b are consecutive even numbers their LCM is a*b/2;

HCF of fractions = HCF of numerator / LCM of denominator;

LCM of fractions = LCM of numerators / HCF of denominators;

Number of zeroes at the end of the factorial = n!
[ n/5 ] + [ n/5^2 ] + [ n/5^3 ] ....

If a number "a" divides another number "b" exactly, we say that "a" is a factor of "b". In this case, "b" is called a multiple of "a".

Suppose we have to find the H.C.F. of three numbers. Then, H.C.F. of [(H.C.F. of any two) and (the third number)] gives the H.C.F. of three given numbers.

Product of two numbers = Product of their H.C.F. and L.C.M

Co-primes: Two numbers are said to be co-primes if their H.C.F. is 1

H.C.F. and L.C.M. of Fractions :

HCF = \( \frac{\text{H.C.F. of Numerators}}{\text{L.C.M. of Denominators}} \)

LCM = \( \frac{\text{L.C.M. of Numerators}}{\text{H.C.F. of Denominators}} \)

H.C.F. and L.C.M. of Decimal Fractions : In given numbers, make the same number of decimal places by annexing zeros in some numbers, if necessary. Considering these numbers without decimal point, find H.C.F. or L.C.M. as the case may be. Now, in the result, mark off as many decimal places as are there in each of the given numbers.

HCF of two consecutive even numbers is 2. HCF of two consecutive odd numbers is 1.

If the HCF of x and y is G, then the HCF of x, (x + y) is also G. x, (x - y) is also G

HCF of \( (a^m - 1) \text{ and } (a^n - 1) \text{ is given by } (a^{\text{HCF of } m,n} -1 ) \)

Suppose you were required to find the HCF of 39, 78 and 195

The HCF of these numbers would necessarily have to be a factor (divisor) of the difference between any pair of numbers from the above 3. i.e. the HCF has to be a factor of (78 – 39 = 39) as well as of (195 – 39 = 156) and (195 – 78 = 117).

Usually select the two closest numbers to subtract. In above example use 78 and 39.

After subtraction, we get 39. The HCF of the given numbers 39, 78 , 195 will always be among the factors of 39.

The factors of 39 are 1,3,13,39.

Hence, one of these 4 numbers has to be the HCF of the numbers 39,78 and 195. Since we are trying to locate the Highest common factor we would begin our search from the highest number 39. In this case, 39 is the HCF.

Rules of Co-prime numbers :

Two consecutive natural numbers are always co-prime

Two consecutive odd numbers are always co-prime

Two prime numbers are always co-prime

One prime number and another composite number (such that the composite number is not a multiple of the prime number) are always co-prime (Examples: 17, 38; 23, 49 and so on, but note that 17 and 51 are not co-prime)

Three or more numbers being co-prime with each other means that all possible pairs of the numbers would be co-prime with each other. Thus, 47, 49, 51 and 52 are co-prime since each of the 6 pairs (47,49); (47,51); (47,52); (49,51); (49,52) and (51,52) are co-prime.

Three consecutive odd numbers are always co-prime

Three consecutive natural numbers with the first one being odd are coprime

Two consecutive natural numbers along-with the next odd number such that the first no. is even (examples: 22, 23, 25; 52, 53, 55; 68, 69, 71 and so on)

Three prime numbers (Examples: 17, 23, 29; 13, 31, 43 and so on)

Let us say that you were trying to find the LCM of 9,10,12 and 15. The rules of Co-prime numbers are beneficial for you !

Step 1 : If you can see a set of 2 or more co-prime numbers in the set of numbers for which you are finding the LCM write them down by multiplying them. So in the above situation, since we can see that 9 and 10 are co-prime to each other we can start off writing the LCM by writing 9 * 10 as the first step.

Step 2 : For each of the other numbers, consider what part of them have already been taken into the answer and what part remains outside the answer. In case you see any part of the other numbers such that it is not a part of the value of the LCM you are writing such a part would need to be taken into the answer of the LCM.

Thought about 12 : 12 is 2 * 2 * 3. 9 * 10 already has a 3 and one 2 in it prime factors. However, the number 12 has two 2's. This means that one of the two 2’s of the number 12 is still not accounted for in our answer. Hence, we need to modify the LCM by multiplying the existing 9 * 10 by a 2. With this change the LCM now becomes: 9 * 10 * 2

Thought bout 15 : 15 is 5 * 3, however the term 9 * 10 * 2 already has 5 and 3 . Hence there is no need for additionally having a 5 * 3 in the LCM. Hence, the LCM is 9 * 10 * 2.

Find the HCF of (3¹²⁵ – 1) and (3³⁵ – 1).

3²⁵ – 1

3⁵ – 1

3¹²⁵ – 1

3³⁵ – 1

Ans .

3⁵ – 1

Explanation :
The HCF of (a^m – 1) and (a²⁵ – 1) is given by (a^{HCF of m, n} – 1) Thus, in this question the answer is: (3⁵ – 1). Since 5 is the HCF of 35 and 125.]

The smallest square number, which is exactly divisible by 2, 3, 4, – 9, 6, 18, 36 and 60, is

900

1600

3600

none

Ans .

Explanation :

The LCM of the given numbers is 180. Hence, all multiples of 180 would be divisible by all of
these numbers. Checking the series 180, 360, 540, 720, 900 we can see that 900 is the first perfect
square in the list. Option (a) is correct.

HCF of \( 2^3 * 3^3 * 5 * 7^4 , 2^2 * 3^5 * 5^2 * 7^3 , 2^3 * 5^3 * 7^2\)

1080

970

960

980

Ans .

980

Explanation :
The prime numbers common to given numbers are 2,5 and 7. HCF = \( 2^2 * 5 * 7^2 = 980 \)

If two given numbers are divisible by a number, then their difference is also divisible by that number.

true

false

cant say

only if numbers are not consecutive

Ans .

true

Explanation :
If two given numbers are divisible by a number, then their difference is also divisible by that number.

Two tankers contain 850 litres and 680 litres of kerosene oil respectively. Find the maximum capacity of a container which can measure the kerosene oil of both the tankers when used an exact number of times

170

470

370

270

Ans .

170

Explanation :
The required container has to measure both the tankers in a way that the count is an exact number of times. So its capacity must be an exact divisor of the capacities of both the tankers. Moreover, this capacity should be maximum. Thus, the maximum capacity of such a container will be the HCF of 850 and 680. The common factors of 850 and 680 are 2, 5 and 17. Thus, the HCF of 850 and 680 is 2 × 5 × 17 = 170. Therefore, maximum capacity of the required container is 170 litres. It will fill the first container in 5 and the second in 4 refill

. In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm and 90 cm respectively . What is the minimum distance each should walk so that all can cover the same distance in complete steps?

12040

12140

12240

12340

Ans .

12240

Explanation :
The distance covered by each one of them is required to be the same as well as minimum. The required minimum distance each should walk would be the lowest common multiple of the measures of their steps. Thus, we find the LCM of 80, 85 and 90. The LCM of 80, 85 and 90 is 12240. The required minimum distance is 12240 cm.

Find the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case.

144

154

164

151

Ans .

151

Explanation :
first find the LCM of 12, 16, 24 and 36. We get LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144. 144 is the least number which when divided by the given numbers will leave remainder 0 in each case. But we need the least number that leaves remainder 7 in each case. Therefore, the required number is 7 more than 144. The required least number = 144 + 7 = 151.

Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.

Ans .

Explanation :
Find the HCF of the weights. the maximum value of weight which can measure the weight of the fertiliser exact number of times is the HCF (75, 69) = 3.

Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the distance in complete steps?

3930

8930

6930

7930

Ans .

6930

Explanation :
The minimum distance each should cover so that all can cover the distance in complete steps is LCM (63,70,77) = 6930.

The length, breadth and height of a room are 825 cm, 675 cm and 450 cm respectively. Find the longest tape which can measure the three dimensions of the room exactly.?

Ans .

Explanation :
longest tape which can measure the three dimensions of the room exactly is HCF (825,675,450) = 75 cm

Determine the smallest 3-digit number which is exactly divisible by 6, 8 and 12. ?

520

120

220

Ans .

120

Explanation :
smallest number which is exactly divisible by 6, 8 and 12 is LCM (6,8,12) = 24. So 24 * 3 = 120 is the smallest 3 digit number.

Determine the greatest 3-digit number exactly divisible by 8, 10 and 12. ?

990

970

960

950

Ans .

960

Explanation :
greatest 3-digit number exactly divisible by 8, 10 and 12 is multiple of the LCM (10,8,12) = 120. So 120 * 8 = 960 is the greatest 3 digit number.

The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m., at what time will they change simultaneously again? ?

7:09:12

7:04:12

7:05:12

7:07:12

Ans .

Explanation :
Time they will change again is LCM of 48,72,108 i.e 432 = 7 min and 12 secs. So they will change again at 7:07:12 am

Three tankers contain 403 litres, 434 litres and 465 litres of diesel respectively. Find the maximum capacity of a container that can measure the diesel of the three containers exact number of times.

Ans .

Explanation :
HCF of 403,434,465 = 31

Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case

Ans .

Explanation :
LCM of 6,15,18 = 90. So answer is 90 + 5 = 95

Find the smallest 4-digit number which is divisible by 18, 24 and 32.

1452

1352

1152

1252

Ans .

1152

Explanation :
LCM of 18, 24, 32 = 288. So answer is 288 * 4 = 1152.

Find the H.C.F. of 108, 288 and 360

Ans .

Explanation :
Sol. 108 = 2² x 3³ , 288 = 2⁵ x 3² and 360 = 2³ x 5 x 3². H.C.F. = 2² x 3² = 36.

Find the H.C.F. of 513, 1134 and 1215

Ans .

Explanation :

Reduce \( \frac{391}{667} \) to lowest terms.

12/29

14/29

15/29

17/29

Ans .

17/29

Explanation :
H.C.F. of 391 and 667 is 23. On dividing the numerator and denominator by 23, we get : \( \frac{391}{667} = \frac{17}{29} \)

Find the LCM of \( 2^2 * 3^3 * 5 * 7^2, 2^3 * 3^2 * 5^2 * 7^4, 2 * 3 * 5^3 * 7 * 11 \)

2³ * 3³ * 5³ * 7⁴ * 11

2² * 3³ * 5³ * 7⁴ * 11

2³ * 3² * 5³ * 7⁴ * 11

2¹ * 3¹ * 5¹ * 7¹ * 11

Ans .

2³ * 3³ * 5³ * 7⁴ * 11

Explanation :
L.C.M. = Product of highest powers of 2, 3, 5, 7 and 11 = 2³ * 3³ * 5³ * 7⁴ * 11

Find the L.C.M. of 72, 108 and 2100

37800

47800

57800

6800

Ans .

37800

Explanation :
\( 72 = 2^3 * 3^2 ; 108 = 3^3 * 2^2, 2100 = 2^2 * 5^2 * 3 * 7; LCM = 2^3 * 3^3 * 5^2 * 7 = 37800 \)

Find the L.C.M. of 16, 24, 36 and 54

432

442

132

232

Ans .

432

Explanation :

Find the H.C.F. and L.C.M. of \( \frac{2}{3}, \frac{8}{9}, \frac{16}{81}, \frac{10}{27} \)

2/81 and 80/3

4/81 and 40/3

6/81 and 80/3

7/81 and 80/3

Ans .

2/81 and 80/3

Explanation :
HCF of fractions = \( \frac{H.C.F. of 2,8,16,10}{L.C.M. of 3,9,81,27} = \frac{2}{81} \) and LCM of fractions = \( \frac{LCM of 2,8,16,10}{HCF. of 3,9,81,27} = \frac{80}{3} \)

Find the H.C.F. and L.C.M. of 0.63, 1.05 and 2.1.

0.21 and 6.30

2.1 and 6.30

0.21 and 0.63

0.021 and 0.063

Ans .

0.21 and 6.30

Explanation :
Making the same number of decimal places, the given numbers are 0.63, 1.05 and 2.10. Without decimal places, these numbers are 63, 105 and 210. Now, H.C.F. of 63, 105 and 210 is 21. H.C.F. of 0.63, 1.05 and 2.1 is 0.21. L.C.M. of 63, 105 and 210 is 630. L.C.M. of 0.63, 1.05 and 2.1 is 6.30.

Two numbers are in the ratio of 15:11. If their H.C.F. is 13, find the numbers.

205 and 143

195 and 153

195 and 143

195 and 163

Ans .

195 and 143

Explanation :
Let the required numbers be 15.x and llx. Then, their H.C.F. is x. So, x = 13. The numbers are (15 x 13 and 11 x 13) i.e., 195 and 143

The H.C.F. of two numbers is 11 and their L.C.M. is 693. If one of the numbers is 77, find the other

693

Ans .

Explanation :
other number = \( \frac{11 X 693}{77} = 99 \)

Find the greatest possible length which can be used to measure exactly the lengths 4 m 95 cm, 9 m and 16 m 65 cm

Ans .

Explanation :
Required length = H.C.F. of 495 cm, 900 cm and 1665 cm. 495 = 3² x 5 x 11, 900 = 2² x 3² x 5² , 1665 = 3² x 5 x 37. H.C.F. = 32 x 5 = 45. Hence, required length = 45 cm.

Find the greatest number which on dividing 1657 and 2037 leaves remainders 6 and 5 respectively.

117

125

127

123

Ans .

Explanation :
Required number = H.C.F. of (1657 - 6) and (2037 - 5) = H.C.F. of 1651 and 2032. Required number = 127.

Find the largest number which divides 62, 132 and 237 to leave the same remainder in each case.

Ans .

Explanation :
Required number = H.C.F. of (132 - 62), (237 - 132) and (237 - 62) = H.C.F. of 70, 105 and 175 = 35.

Find the least number exactly divisible by 12,15,20,27.

540

542

550

560

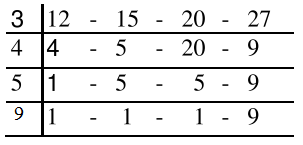
Ans .

540

Explanation :

Find the least number which when divided by 6,7,8,9, and 12 leave the same remainder 1 each case

502

553

503

505

Ans .

505

Explanation :
Required number = (L.C.M OF 6,7,8,9,12) + 1. L.C.M = 3 X 2 X 2 X 7 X 2 X 3 = 504. Hence required number = (504 +1) = 505.

Find the largest number of four digits exactly divisible by 12,15,18 and 27

9710

9740

9730

9720

Ans .

9720

Explanation :
The Largest number of four digits is 9999. Required number must be divisible by L.C.M. of 12,15,18,27 i.e. 540. On dividing 9999 by 540,we get 279 as remainder . Required number = (9999-279) = 9720.

Find the smallest number of five digits exactly divisible by 16,24,36 and 54.

10358

11368

10368

10268

Ans .

10368

Explanation :
Smallest number of five digits is 10000. Required number must be divisible by L.C.M. of 16,24,36,54 i.e 432, On dividing 10000 by 432,we get 64 as remainder. Required number = 10000 +( 432 – 64 ) = 10368.

Find the least number which when divided by 20,25,35 and 40 leaves remainders 14,19,29 and 34 respectively.

1594

1394

1564

1494

Ans .

1394

Explanation :
Here,(20-14) = 6,(25 – 19)=6,(35-29)=6 and (40-34)=6. Required number = (L.C.M. of 20,25,35,40) – 6 = 1394.

Find the least number which when divided by 5,6,7, and 8 leaves a remainder 3, but when divided by 9 leaves no remainder

1483

1583

1683

1693

Ans .

1683

Explanation :
L.C.M. of 5,6,7,8 = 840. Required number is of the form 840k + 3 Least value of k for which (840k + 3) is divisible by 9 is k = 2. Required number = (840 X 2 + 3) = 1683

The traffic lights at three different road crossings change after every 48 sec., 72 sec and 108 sec.respectively .If they all change simultaneously at 8:20:00 hours,then at what time they again change simultaneously .

8:27:20

8:27:23

8:27:24

8:27:12

Ans .

8:27:12

Explanation :
Interval of change = (L.C.M of 48,72,108)sec.=432sec. So, the lights will agin change simultaneously after every 432 seconds i.e,7 min.12sec Hence , next simultaneous change will take place at 8:27:12 hrs

Arrange the fractions \( \frac{17}{18} , \frac{31}{36} , \frac{43}{45} , \frac{59}{60} \) in the ascending order

31/36 , 17/18, 43/45, 59/60

17/18 , 31/36 ,43/45, 59/60

43/45, 31/36 , 17/18, 59/60

31/36 , 43/45, 59/60 , 17/18,

Ans .

31/36 , 17/18, 43/45, 59/60

Explanation :
L.C.M. of 18,36,45 and 60 = 180. \( \frac{17}{18} = \frac{17 * 10}{18 * 10} = \frac{170}{180} \) and \( \frac{31}{36} = \frac{31*5}{36*5} = \frac{155}{180} \) , \( \frac{43}{45} = \frac{43*4}{45*4} = \frac{172}{180} \), \( \frac{59}{60} = \frac{59*3}{60*3} = \frac{177}{180} \). Comparing the numerators as all denominators are same we get the answer.

Quiz

Score more than 80% marks and move ahead else stay back and read again!

upscfever.com

Chapter 2: NUMBER THEORY

Introduction

Formulae of HCF and LCM

Strategy for Finding the GCD

Strategy for Finding LCM

Solved Questions

Quiz

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments