-
Chapter 4: SQUARE AND CUBE ROOTS
Introduction
The straight line method of multiplying two numbers
Suppose you were multiplying two 2 digit numbers like 43 × 78. The first objective would be to get the unit’s digit. In order to do this we just need to multiply the units’ digit of both the numbers. Thus, 3 × 8 would give us 24. Hence, we would write 4 in the units’ digit of the answer and carry over the digit 2 to the tens place.
Step 2: Finding the tens’ place digit Multiply the units digit of second number to tens digit of first. Multiply units digit of first to tens digit of second. Add both results and any carry forward received from the operation on step 1. Thus we would get: 8 (units digit of the second number) × 4 (tens digit of the first number) + 7 (tens digit of the second number) × 3 (units digit of the first number + 2 (carry over from the units’ digit calculation) = 32 + 21 + 2 = 55.
Step 3: Finding the hundreds’ place digitMultiply the tens digit of both numbers and add previous carry to it.
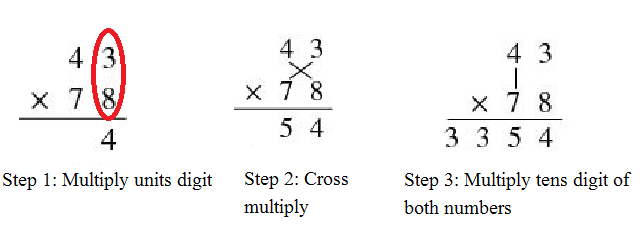
Multiply a three digit number to a two digit number
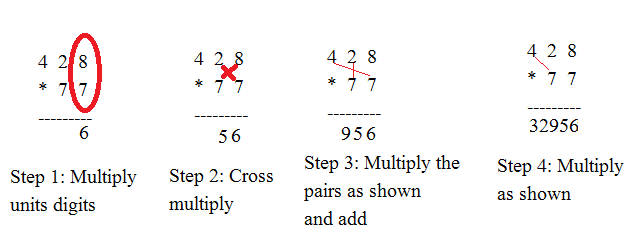
Step 1:Get the units digit by multiplying the units terms of both numbers. here, we get 8 * 7 = 56 so keep 6 and carry forward 5 to the next operation.
Step 2:The next digit is obtained by cross multiplying the digits as shown and adding any carry. For this we get 8*7 + 7*2 + 5 = 75. So we carry forward 7 and leave 5 behind.
Step 3:for the next digit we cross multiply as shown and add the carry if any. here it is 28 + 14 + 7 = 49. So 9 is kept and 4 is the carry.
Step 4:Finally we get the final digit. Here we get 4 * 7 + 4 = 32.
Multiply a three digit number to a three digit number
Step 1:Get the units digit by multiplying the units terms of both numbers. here we have to multiply 8 * 7 = 56, so we keep 6 and carry forward 5.
Step 2:The next digit is obtained by cross multiplying the digits as shown and adding any carry. Then we cross multiply to get 7*2 + 8*7 + 5 = 75. We keep 5 and carry forward 7.
Step 3:for the next digit we cross multiply as shown and add the carry if any. Here it is 4 * 7 + 2 * 7 +1 * 8 +7 = 57. we keep 7 and carry forward 5.
Step 4:For the fourth digit we cross multiply as shown: 4 * 7 + 2 * 1 + 5 = 35, we keep 5 and carry forward 3.
Step 5:Finally we get the final digit we multiply 4 * 1 + 3 = 7.

Squares and cubes of numbers up to 20
| Number | Square | Cube |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 8 |
| 3 | 9 | 27 |
| 4 | 16 | 64 |
| 5 | 25 | 125 |
| 6 | 36 | 216 |
| 7 | 49 | 343 |
| 8 | 64 | 512 |
| 9 | 81 | 729 |
| 10 | 100 | 1000 |
| 11 | 121 | 1331 |
| 12 | 144 | 1728 |
| 13 | 169 | 2197 |
| 14 | 196 | 2744 |
| 15 | 225 | 3375 |
| 16 | 256 | 4096 |
| 17 | 289 | 4913 |
| 18 | 324 | 5832 |
| 19 | 361 | 6859 |
| 20 | 400 | 8000 |
| 21 | 441 | |
| 22 | 484 | |
| 23 | 529 | |
| 24 | 576 | |
| 25 | 625 | |
| 26 | 676 | |
| 27 | 729 | |
| 28 | 784 | |
| 29 | 841 | |
| 30 | 900 |
Methods to find the Squares
Method to find the Square of the number between 51 - 80
Suppose, we want to find the square of 67; We write it as (50 + 17)2.
The last two digits of 672 are obtained from the last two digits of square of 17 which is 289 . Hence 89 is kept and two is carried forward.
The first two digits are found by addition of 25 + 17 + 2 = 44. 25 is the standard number to be used in all cases, 17 is due to 67 being 50 + 17. And 2 is from the previous operation.
Thus, we get the square of 67 as 4489.
Method to find the Square of the number between 31 - 50
Look at 41 as (50 – 9).
The last two digits are got by the last two digits in the value of (– 9) 2 = 81. Hence, 81 will represent the last two digits of 412.
The first two digits are derived by 25 – 9 = 16 (where 25 is a standard number to be used in all cases and – 9 comes from the fact that (50 – 9) = 41).
Hence, the answer is 1681. In case there had been a carry over from the last two digits it would have been added to 16 to get the answer.
Method to find the Square of the number between 81 - 100
Suppose you have to find the value of 822. The following process will give you the answers. Look at 82 as (100 – 18). The answer will have 4 digits whose values will be got by focusing on getting the value of the last two digits and that of the first two digits.
The value of the last two digits will be equal to the last two digits of ( – 18)2 . Since, ( – 18)2 = 324, the last two digits of 822 will be 24. The ‘3’ in the hundreds place of (– 18)2 will be carried over to the other part of the answer (i.e. the first two digits).
The first two digits will be got by: 82 + (– 18) + 3 Where 82 is the original number; (– 18) is the number obtained by looking at 82 as (100 – x); and 3 is the carry over from (– 18)2
Hence answer is 6724
Obtain the square of any number ending with 5 :
The last two digits will always be 25. The digits before that in the answer will be got by multiplying the digits leading up to the digit 5 in the number by 1 more than itself. Example : 252 = 625 i.e. ___25 and ___ is 2 * (2 + 1) = 2*3 = 6
Properties of Squares and Cubes
The difference between the squares of two consecutive natural numbers is always equal to the sum of the natural numbers. Thus, 412 – 402 = (40 + 41) = 81. This property is very useful when used in the opposite direction i.e. Given that the difference between the squares of two consecutive integers is 81, you should immediately realise that the numbers should be 40 and 41.
The square of a number ending in 1, 5 or 6 also ends in 1, 5 or 6 respectively.
The value of a perfect square has to end in 1, 4, 5, 6, 9 or an even number of zeros. In other words, a perfect square cannot end in 2, 3, 7, or 8 or an odd number of zeros.
The sum of the squares of the first ‘n’ natural numbers is given by \( \frac{n(n+1)(2n+1)}{6} \)
Factorization method to get square root
To find the square root of a perfect square by using the prime factorization method when a given number is a perfect square:
Step I: Resolve the given number into prime factors.
Step II: Make pairs of similar factors.
Step III: Take the product of prime factors, choosing one factor out of every pair.
Square Root
What is the number you want to find the square root of?
Here's one we'll use:
46656
First, divide the number to be square-rooted into pairs of digits, starting at the decimal point. That is, no digit pair should straddle a decimal point. (For example, split 1225 into "12 25" rather than "1 22 5"; 6.5536 into "6. 55 36" rather than"6.5 53 6".)
Then you can put some lines over each digit pair, and a bar to the
left, somewhat as in long division.
+--- ---- ----
| 4 66 56
Find the largest number whose square is less than or equal to the leading digit pair. In this case, the leading digit pair is 4; the largest number whose square is less than or equal to 4 is 2.
Put that number on the left side, and above the first digit pair.
2
+--- ---- ----
2 | 4 66 56
Now square that number, and subtract from the leading digit pair.
2
+--- ---- ----
2 | 4 66 56
|-4
+----
0
Extend the left bracket; multiply the last (and only) digit of the left-hand
number by 2, put it to the left of the difference you just calculated, and
leave an empty decimal place next to it.
2
+--- ---- ----
2 | 4 66 56
|-4
+----
4_ | 0
Then bring down the next digit pair and put it to the right
of the difference.
2
+--- ---- ----
2 | 4 66 56
|-4
+----
4_ | 0 66
Find the largest number to put in this blank decimal place such that that
number, times the number already there plus the decimal place, will be less
than the current difference. For example, see if 1 * 41 is ≤ 66, then 2*42
≤ 66, etc. In this case it's a 1. Put this number in the blank you left,
and in the next decimal place on the result row on the top.
2 1
+--- ---- ----
2 | 4 66 56
|-4
+----
41 | 0 66
Now subtract the product you just found.
2 1
+--- ---- ----
2 | 4 66 56
|-4
+----
41 | 0 66
|- 41
+--------
25
Now, repeat as before: Take the number in the left column (here, 41) and
double its last digit (giving you 42). Copy this below in the left column, and
leave a blank space next to it. (Double the last digit with carry: for
example, if you had not 41 but 49, which is 40+9, you should copy down 40+18
which is 58.) Also, bring down the next digit pair on the right.
2 1
+--- ---- ----
2 | 4 66 56
|-4
+----
41 | 0 66
|- 41
+--------
42_ 25 56
Now, find the largest digit (call it #) such that 42# * # ≤ 2556. Here,
it turns out that 426 * 6 = 2556 exactly.
2 1 6
+--- ---- ----
2 | 4 66 56
|-4
+----
41 | 0 66
|- 41
+--------
426 | 25 56
|- 25 56
+-------------
0
When the difference is zero, you have an exact square root and you're done. Otherwise, you can keep finding more decimal places for as long as you want.
Here is another example, with less annotation.
7 . 2 8 0 1 ...
+----------------------
7 | 53 . 00 00 00 00 00
| 49
+----------------------
142 | 4 00
| 2 84
+----------------------
1448 | 1 16 00
| 1 15 84
+----------------------
14560 | 16 00
| 0
+----------------------
145601 | 16 00 00
| 14 56 01
+----------------------
| 1 43 99 00
...
Rules to obtain Square Root of a Number
\( \sqrt{xy} = \sqrt{x} * \sqrt{y}\)
\( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} = \frac{\sqrt{xy}}{\sqrt{y}}\)
Solved Question Papers
Ans .
16
- Explanation :
\( \sqrt{248 + \sqrt{51 + 13}} = \sqrt{248 + \sqrt{64}} = \sqrt{256} = 16\)
Ans .
3
- Explanation :
\( \frac{\sqrt{(6 + 2)(15 + 3)}}{3 + 1} = \sqrt{8 * 18} / 4 = \sqrt{144}/4 = 3\)
Ans .
5/4
- Explanation :
\( \sqrt{25/16} = 5/4 \)
Ans .
0.03
- Explanation :
\( \sqrt{0.0009} = \sqrt{\frac{9}{1000}} = 3/100 = 0.03 \)
Ans .
13.24
- Explanation :

Ans .
8.1
- Explanation :
\( \sqrt{32.4/x} = 2; Then, 32.4/x = 4 <=> 4x = 32.4 <=> x = 8.1\)
Ans .
2
- Explanation :
\( \sqrt{86.49} + \sqrt{5 + x^2} = 12.3 ; 9.3 + \sqrt{5 + x^2} = 12.3; \sqrt{5 + x^2} = 12.3 - 9.3 = 3; 5 + x^2 = 9; x^2 = 9-5 ; x = 2\)
Ans .
170 / 11
- Explanation :
√0.289/0.00121 = √0.28900/0.00121 = √28900/121 = 170 / 11
Ans .
25
- Explanation :
√1 + (x / 144) = 13 / 12 -> ( 1 + (x / 144)) = (13 / 12 )2 = 169 / 144 -> x / 144 = (169 / 144) - 1 ; -> x / 144 = 25/144 -> x = 25.
Ans .
1.732
- Explanation :

Ans .
1.732
- Explanation :
√192 - (1 / 2)√48 - √75 = √(64 * 3) - (1/2) √ (16 * 3) - √ (25 * 3) =8√3 - (1/2) * 4√3 - 5√3 =3√3 - 2√3 = √3 = 1.732
Ans .
150
- Explanation :
Given exp. = √(9.5 * 0.0085 * 18.9) / (0.0017 * 1.9 * 0.021) Now, since the sum of decimal places in the numerator and denominator under the radical sign is the same, we remove the decimal. Given exp = √(95 * 85 * 18900) / (17 * 19 * 21) = √ (5 * 5 * 900) = 5 * 30 = 150
Ans .
4
- Explanation :
\( \sqrt{[(12.1+8.1)(12.1-8.1)]/[(0.25)(0.25+19.95)]}; \sqrt{(20.2 * 4) /( 0.25 * 20.2) } ; = \sqrt{4/0.25}; = \sqrt{400/25} = 4\)
Ans .
6
- Explanation :
x2 + y2 = (1 + √2)2 + (1 - √2)2 = 2[(1)2+ (√2)2] = 2 * 3 = 6.
Ans .
0.948
- Explanation :

Ans .
1.2933
- Explanation :
√ (5/3) = √(5 * 3) / (3 * 3) = √(15 / 3) = 3.88 / 3 = 1.2933
Ans .
900
- Explanation :
L.C.M. of 10, 12, 15, 18 = 180. Now, 180 = 2 * 2 * 3 * 3 *5 = 22 * 32 * 5. To make it a perfect square, it must be multiplied by 5. Required number = (22 * 32 * 52) = 900
Ans .
99856
- Explanation :

Ans .
69
- Explanation :
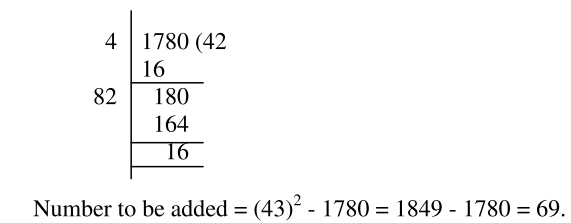
Ans .
0.4142
- Explanation :
√2 / (2 + √2) = √2 / (2 + √2) * (2 - √2) / (2 - √2) = (2√2 – 2) / (4 – 2) = 2(√2 – 1) / 2 = √2 – 1 = 0.4142.
Ans .
62
- Explanation :
x = [(√5 + √3) / (√5 - √3)] * [(√5 + √3) / (√5 + √3)] = (√5 + √3)2 / (5 - 3) =(5 + 3 + 2√15) / 2 = 4 + √15. y = [(√5 - √3) / (√5 + √3)] * [(√5 - √3) / (√5 - √3)] = (√5 - √3)2 / (5 - 3) =(5 + 3 - 2√15) / 2 = 4 - √15. x2 + y2 = (4 + √15)2 + (4 - √15)2 = 2[(4)2 + (√15)2] = 2 * 31 = 62.
Ans .
14
- Explanation :
2744 = 23 x 73 3√2744= 2 x 7 = 14.
Ans .
50
- Explanation :
Clearly, 4320 = 23 * 33 * 22 * 5. To make it a perfect cube, it must be multiplied by 2 * 52 i.e, 50.
Q. Take square root of 484
 484 = 2^2 * 11^2
484 = 2^2 * 11^2
So square root of 484 = square root 2^2 * 11^2 = 2*11 = 22
Q. Which number should be multiplied with 675 to get a perfect cube.
A. 675 = 5*5*3*3*3. Therefore another 5 needs to be multiplied to get perfect cube.
Q.
Assume the value be x.
Squaring both sides,
or x = 4 as x can't be negative.
Q. if square root of 3 = 1.732 find square root of 192.
A. 192 = 3 * 2 * 2 * 2 * 2 * 2 * 2 so
square root of 192 = 8 * square root (3)
Ans .
241
- Explanation :
Clearly, 16 > Square-Root(241). Prime numbers less than 16 are 2, 3, 5, 7, 11, 13. 241 is not divisible by any one of them. 241 is a prime number.
Ans .
yes
- Explanation :
Clearly, 19 > Square-Root(337). Prime numbers less than 19 are 2, 3, 5, 7, 11,13,17. 337 is not divisible by any one of them. 337 is a prime number.
Ans .
no
- Explanation :
Clearly, 20 > Square-root(391). Prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, 19. We find that 391 is divisible by 17. 391 is not prime
Ans .
no
- Explanation :
Clearly, 24 > Square-root(571). Prime numbers less than 24 are 2, 3, 5, 7, 11, 13, 17, 19, 23. 571 is not divisible by any one of them. 571 is a prime number.
Quiz
Score more than 80% marks and move ahead else stay back and read again!
Level II Difficulty Questions
Ans .
1
- Explanation :
The only value that will satisfy will be 2.
Ans .
6
- Explanation :
¼ + 1/6 will give you 5/12.
Ans .
6
- Explanation :
The possible values are 1, 2, 3, 4, 6 and 12. (i.e. the factors of 12)
Ans .
9
- Explanation :
k will be a number of the form 7n + 3. Hence, if you take the value of n as 9, k + 2n will become 7n + 3 + 18 = 7n + 21. This number will be divisible by 7. The numbers 3, 5 and 7 do not provide us with this solution
Ans .
2
- Explanation :
273 – 272 – 271 = 271(22 – 2 – 1) = 271. Hence option (c) is correct.
Ans .
always divisible by 24
- Explanation :
Property of prime numbers greater than 5