Chapter 16: ARITHMETIC REASONING

Introduction

read and answer

Each of these questions is followed by two statements, I and II. Mark the answer as
(a) if the question can be answered with the help of statement I alone.
(b) if the question can be answered with the help of statement II alone.
(c) if both statement I and statement II are needed to answer the question.
(d) if the question cannot be answered even with the help of both the statements.

Q.If x, y and z are real numbers, is z – x even or odd?
I. xyz is odd.
II. xy + yz + zx is even.

1. a
2. b
3. c
4. d

Ans.a

Q.What is the value of x, if x and y are consecutive positive even integers?
I. (x – y)² = 4
II. (x + y)² < 100

1. a
2. b
3. c
4. d

Ans.d

Q.What is the profit percentage?
I. The cost price is 80% of the selling price.
II. The profit is Rs.50.

1. a
2. b
3. c
4. d

Ans.a

Q.What is the area of the triangle?
I. Two sides are 41 cm each.
II. The altitude to the third side is 9 cm long.

1. a
2. b
3. c
4. d

Ans.c

Q.What is the price of bananas?
I. With Rs.84, I can buy 14 bananas and 35 oranges.
II. If price of bananas is reduced by 50%, then we can buy 48 bananas in Rs.12.

1. a
2. b
3. c
4. d

Ans.b

Q.What is the first term of an arithmetic progression of positive integers?
I. Sum of the squares of the first and the second term is 116.
II. The fifth term is divisible by 7.

1. a
2. b
3. c
4. d

Ans.a

Q.What is the length of rectangle ABCD?
I. Area of the rectangle is 48 square units.
II. Length of the diagonal is 10 units.

1. a
2. b
3. c
4. d

Ans.c

Q.What is the number x?
I. The LCM of x and 18 is 36.
II. The HCF of x and 18 is 2.

1. a
2. b
3. c
4. d

Ans.c

Q.Is x + y – z + t even?
I. x + y + t is even.
II. t and z are odd.

1. a
2. b
3. c
4. d

Ans.c

Q.Boxes numbered 1, 2, 3, 4 and 5 are kept in a row, and they are to be filled with either a red or a blue ball, such that no two adjacent boxes can be filled with blue balls. Then how many different arrangements are possible, given that all balls of a given colour are exactly identical in all respects?

1. 8
2. 10
3. 15
4. 13

Ans.d

Q.A, B, C and D are four towns, any three of which are non-collinear. Then the number of ways to construct three roads each joining a pair of towns so that the roads do not form a triangle is

1. 7
2. 8
3. 9
4. 24

Ans.d

Read and Answer - Arithmetic reasoning

Each question is followed by two statements, I and II. Mark the answer as
(a) if the question cannot be answered even with the help of both the statements taken together.
(b) if the question can be answered by any one of the two statements.
(c) if each statement alone is sufficient to answer the question, but not the other one (E.g. statement I alone is required to answer the question, but not statement II and vice versa).
(d) if both statements I and II together are needed to answer the question.

Q.A tractor travelled a distance 5 m. What is the radius of the rear wheel?
I. The front wheel rotates ‘N’ times more than the rear wheel over this distance.
II. The circumference of the rear wheel is ‘t’ times that of the front wheel.

1. a

2. b

3. c

4. d

Ans.a

Q.What is the ratio of the two liquids A and B in the mixture finally, if these two liquids kept in three vessels are mixed together? (The containers are of equal volume.)
I. The ratio of liquid A to liquid B in the first and second vessel is 3 : 5, 2 : 3 respectively.
II. The ratio of liquid A to liquid B in vessel 3 is 4 : 3.

1. a

2. b

3. c

4. d

Ans.a

Q.If a, b and c are integers, is (a – b + c) > (a + b – c)?
I. b is negative.
II. c is positive.

1. a

2. b

3. c

4. d

Ans.d

Q.If α and β are the roots of the equation ax²+bx+c=0 then what is the value of α² + β²
I.α + β = -b/a
II.2*α β = c/a

1. a

2. b

3. c

4. d

Ans.d

Q.What is the cost price of the article?
I. After selling the article, a loss of 25% on cost price is incurred.
II. The selling price is three-fourths of the cost price.

1. a

2. b

3. c

4. d

Ans.a

Q.What is the selling price of the article?
I. The profit on sales is 20%.
II. The profit on each unit is 25% and the cost price is Rs. 250.

1. a

2. b

3. c

4. d

Ans.c

Q.How many different triangles can be formed?
I. There are 16 coplanar, straight lines.
II. No two lines are parallel.

1. a

2. b

3. c

4. d

Ans.a

Q.What is the total worth of Lakhiram's assets?
I. A compound interest at 10% on his assets, followed by a tax of 4% on the interest, fetches him Rs. 1,500 this year.
II. The interest is compounded once every four months.

1. a

2. b

3. c

4. d

Ans.d

Q.How old is Sachin in 1997?
I. Sachin is 11 years younger than Anil whose age will be a prime number in 1998.
II. Anil's age was a prime number in 1996.

1. a

2. b

3. c

4. d

Ans.a

Q.What is the number of type-2 widgets produced, if the total number of widgets produced is 20,000?
I. If the production of type-1 widgets increases by 10% and that of type-2 decreases by 6%, the total production remains the same.
II. The ratio in which type-1 and type-2 widgets are produced is 2 : 1.

1. a

2. b

3. c

4. d

Ans.b

Read and answer - Arithmetic reasoning

Mark the answer
(a) if the question can be answered with the help of one statement alone.
(b) if the question can be answered with the help of any one statement independently.
(c) if the question can be answered with the help of both statements together.
(d) if the question cannot be answered even with the help of both statements together.

Q.What is the value of a³ + b³
I. a² + b² = 22
II. ab = 3

1. a

2. b

3. c

4. d

Ans.d

Q.Is the number completely divisible by 99?
I. The number is divisible by 9 and 11 simultaneously.
II. If the digits of the number are reversed, the number is divisible by 9 and 11.

1. a

2. b

3. c

4. d

Ans.b

Q.A person is walking from Mali to Pali, which lies to its north-east. What is the distance between Mali and Pali?
I. When the person has covered 1/3rd of the distance, he is 3 km east and 1 km north of Mali.
II.When the person has covered 2/3rd of the distance, he is 6 km east and 2 km north of Mali.

1. a

2. b

3. c

4. d

Ans.b

Q.What is the value of x and y?
I. 3x + 2y = 45
II. 10.5x + 7y = 157.5

1. a

2. b

3. c

4. d

Ans.d

Q.Three friends P, Q and R are wearing hats, either black or white. Each person can see the hats of the other two persons. What is the colour of P's hat?
I. P says that he can see one black hat and one white hat.
II. Q says that he can see one white hat and one black hat.

1. a

2. b

3. c

4. d

Ans.d

Q.What is the speed of the car?
I. The speed of a car is 10 (km/hr) more than that of a motorcycle.
II. The motorcycle takes 2 hr more than the car to cover 100 km.

1. a

2. b

3. c

4. d

Ans.c

Q.What is the ratio of the volume of the given right circular cone to the one obtained from it?
I. The smaller cone is obtained by passing a plane parallel to the base and dividing the original height in the ratio 1 : 2.
II. The height and the base of the new cone are one-third those of the original cone.

1. a

2. b

3. c

4. d

Ans.b

Q.What is the area bounded by the two lines and the coordinate axes in the first quadrant?
I. The lines intersect at a point which also lies on the lines 3x – 4y = 1 and 7x – 8y = 5.
II. The lines are perpendicular, and one of them intersects the Y-axis at an intercept of 4.

1. a

2. b

3. c

4. d

Ans.c

Q.What is the cost price of the chair?
I. The chair and the table are sold at profits of 15% and 20% respectively.
II. If the cost price of the chair is increased by 10% and that of the table is increased by 20%, the profit reduces by Rs. 20.

1. a

2. b

3. c

4. d

Ans.d

Q.After what time will the two persons Tez and Gati meet while moving around the circular track? Both of them start at the same point and at the same time.
I. Tez moves at a constant speed of 5 m/s, while Gati starts at a speed of 2 m/s and increases his speed by 0.5 m/s at the end of every second thereafter.
II. Gati can complete one entire lap in exactly 10 s.

1. a

2. b

3. c

4. d

Ans.d

Read and choose the correct alternative

Each question is followed by two statements, I and II. Answer the questions based on the statements and mark the answer as
(a) if the question can be answered with the help of any one statement alone but not by the other statement.
(b) if the question can be answered with the help of either of the statements taken individually.
(c) if the question can be answered with the help of both statements together.
(d) if the question cannot be answered even with the help of both statements together

Q. Find the length of AB if ∠ YBC = ∠ XOY = ∠ XAC = 90°
I. Radius of the arc is given.
II. OA = 5

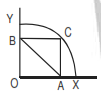
1. A

2. B

3. C

4. D

Ans . D

Q. Is n odd?
I. n is divisible by 3, 5, 7 and 9.
II. 0 < n < 400

1. A

2. B

3. C

4. D

Ans . C

Q. Radha and Rani appeared in an examination. What was the total number of questions?
I. Radha and Rani together solved 20% of the paper.
II. Radha alone solved 3/5 of the paper solved by Rani

1. A

2. B

3. C

4. D

Ans . D

Q. What is the price of tea?
I. Price of coffee is Rs. 5 more than that of tea.
II. Price of coffee is Rs. 5 less than the price of a cold drink which cost three times the price of tea.

1. A

2. B

3. C

4. D

Ans . C

Q. In a group of 150 students, find the number of girls.
I. Each girl was given 50 paise, while each boy was given 25 paise to purchase goods totalling Rs. 49.
II. Girls and boys were given 30 paise each to buy goods totalling Rs. 45.

1. A

2. B

3. C

4. D

Ans . A

Q. There are four racks numbered 1, 2, 3, 4 and four books numbered 1, 2, 3, 4. If an even rack has to contain an odd-numbered book and an odd rack contains an even-numbered book, then what is the position of book 4?
I. Second book has been put in third rack.
II. Third book has been put in second rack.

1. A

2. B

3. C

4. D

Ans . A

Q. Find the value of X in terms of 'a'.
I. Arithmetic mean of X and Y is 'a' while the geometric mean is also 'a'.
II. X/Y = R; X – Y = D.

1. A

2. B

3. C

4. D

Ans . A

Q. A circle circumscribes a square. What is the area of the square?
I. Radius of the circle is given.
II. Length of the tangent from a point 5 cm away from the centre of the circle is given.

1. A

2. B

3. C

4. D

Ans . B

Each question is followed by two statements I and II. Mark:

1. (a) if the question can be answered by any one of the statements alone, but cannot be answered by using the other statement alone.

2. (b) if the question can be answered by using either statement alone.

3. (c) if the question can be answered by using both the statements together, but cannot be answered by using either statement alone.

4. (d) if the question cannot be answered even by using both the statements together

Q. The average weight of students in a class is 50 kg. What is the number of students in the class?
I. The heaviest and the lightest members of the class weigh 60 kg and 40 kg respectively.
II. Exclusion of the heaviest and the lightest members from the class does not change the average weight of the students

1. A

2. B

3. C

4. D

Ans . D

Q. A small storage tank is spherical in shape. What is the storage volume of the tank?
I. The wall thickness of the tank is 1 cm.
II. When an empty spherical tank is immersed in a large tank filled with water, 20 l of water overflow from the large tank.

1. A

2. B

3. C

4. D

Ans . C

Q. Mr X starts walking northwards along the boundary of a field from point A on the boundary, and after walking for 150 m reaches B, and then walks westwards, again along the boundary, for another 100 m when he reaches C. What is the maximum distance between any pair of points on the boundary of the field?
I. The field is rectangular in shape.
II. The field is a polygon, with C as one of its vertices and A as the mid-point of a side.

1. A

2. B

3. C

4. D

Ans . C

Q. A line graph on a graph sheet shows the revenue for each year from 1990 through 1998 by points and joins the successive points by straight-line segments. The point for revenue of 1990 is labelled A, that for 1991 as B, and that for 1992 as C. What is the ratio of growth in revenue between 1991-92 and 1990-91?
I. The angle between AB and X-axis when measured with a protractor is 40°, and the angle between CB and X-axis is 80°.
II. The scale of Y-axis is 1 cm = Rs. 100

1. A

2. B

3. C

4. D

Ans . A

Q. There is a circle with centre C at the origin and radius r cm. Two tangents are drawn from an external point D at a distance d cm from the centre. What are the angles between each tangent and the X-axis?
I. The coordinates of D are given.
II. The X-axis bisects one of the tangents.

1. A

2. B

3. C

4. D

Ans . B

Q. Find a pair of real numbers x and y that satisfy the following two equations simultaneously. It is known that the values of a, b, c, d, e and f are non-zero.
ax + by = c
dx + ey = f
I. a = kd and b = ke, c = kf, k ≠ 0
II. a = b = 1, d = e = 2, f ≠ 2c

1. A

2. B

3. C

4. D

Ans . D

Q. Three professors A, B and C are separately given three sets of numbers to add. They were expected to find the answers to 1 + 1, 1 + 1 + 2, and 1 + 1 respectively. Their respective answers were 3, 3 and 2. How many of the professors are mathematicians?
I. A mathematician can never add two numbers correctly, but can always add three numbers correctly.
II. When a mathematician makes a mistake in a sum, the error is +1 or –1.

1. A

2. B

3. C

4. D

Ans . D

Q. How many students among A, B, C and D have passed the examination?
I. The following is a true statement: A and B passed the examination.
II. The following is a false statement: At least one among C and D has passed the examination

1. A

2. B

3. C

4. D

Ans . C

Q. What is the distance x between two cities A and B in integral number of kilometres?
I. x satisfies the equation log₂x√x
II. x ≤ 10 km

1. A

2. B

3. C

4. D

Ans . C

Q. Mr Mendel grew 100 flowering plants from black seeds and white seeds, each seed giving rise to one plant. A plant gives flowers of only one colour. From a black seed comes a plant giving red or blue flowers. From a white seed comes a plant giving red or white flowers. How many black seeds were used by Mr Mendel?
I. The number of plants with white flowers was 10.
II. The number of plants with red flowers was 70.

1. A

2. B

3. C

4. D

Ans . D