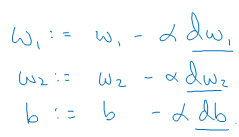Earlier we had set up logistic regression as follows, your predictions, \( \hat{y} \), is defined as follows, where z is given below.

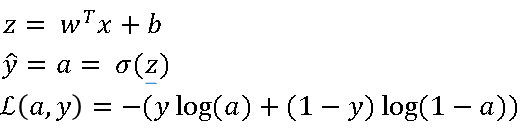
If we focus on just one example for now, then the loss, or respect to that one example, is defined as follows, where A is the output of logistic regression, and Y is the ground truth label.

Let's write this out as a computation graph and for this example, let's say we have only two features, X1 and X2. In order to compute Z, we'll need to input W1, W2, and B, in addition to the feature values X1, X2.

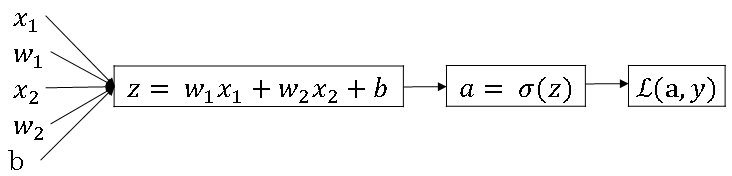
These things, in a computational graph, get used to compute \( Z = W1X1 + W2X2 + B \), rectangular box around that. Then, we compute \( \hat{y} \), or \( a = \sigma(z) \), that's the next step in the computation graph, and then, finally, we compute L(a,y).

In logistic regression, we modify the parameters, W and B, in order to reduce this loss.

We've described the four propagation steps of how you actually compute the loss on a single training example, now let's talk about how you can go backwards to compute the derivatives.

Now what we want to do is compute derivatives with respect to this loss, the first thing we want to do when going backwards is to compute the derivative of this loss with respect to variable A.

In calculus, this ends up being \( -\frac{y}{a} + \frac{1 - y}{1 - a} \)

Going back one more step we can calculate the change in loss with respect to z i.e. \( Dz = \frac{d L(a,y)}{dz}\). It is equal to (a - y).

This result is obtained \( \frac{dL}{da} * \frac{da}{dz} = (a(1-a))*(-\frac{y}{a} + \frac{1 - y}{1 - a}) \).

The final step in that computation is to go back to compute how much you need to change W and B.

In particular, you can show that the derivative with respect to W1 \( = \frac{dL}{dW_1} \) is equal to \( X_1 * (a - y) \). Then, similarly, DW2 \( = \frac{dL}{dW_2} \), which is how much you want to change W2, is \( = X_2 * = (a - y) \) and DB \( = \frac{dL}{dB} \) is equal to \( (a - y) \).

If you want to do gradient descent with respect to just this one example, what you would do is the following; you would use this formula to compute DZ, and then use these formulas to compute DW1, DW2, and DB, and then you perform these updates given below.

W1 gets updated as W1 minus, learning rate alpha, times DW1. W2 gets updated similarly, and B gets set as B minus the learning rate times DB. And so, this will be one step of gradient descent with respect to a single example.