When you build your neural network, one of the choices you get to make is what activation function to use in the hidden layers, as well as what is the output units of your neural network.

So far, we've just been using the sigmoid activation function. But sometimes other choices can work much better.

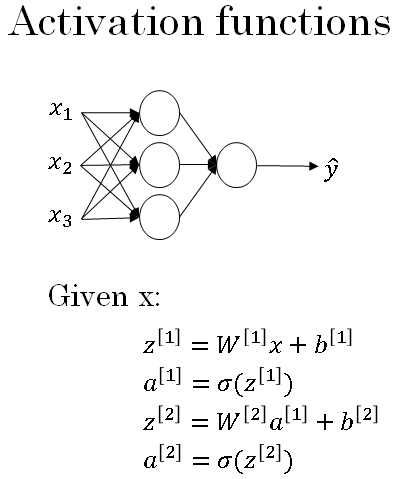
Let's take a look at some of the options. In the forward propagation steps for the neural network, we have these four steps and we use the sigmoid function twice. This is shown below.

Sigmoid is called an activation function. It is shown in below figure.

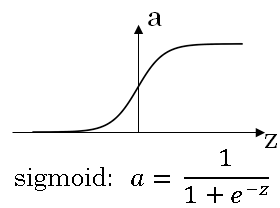
The sigmoid function goes within zero and one, and activation function that almost always works better than the sigmoid function is the tangent function or the hyperbolic tangent function.

This almost always works better than the sigmoid function because the values between + 1 and - 1, the mean of the activations that come out of your head, and they are closer to having a 0 mean.

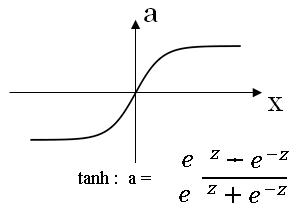
The tanh function is almost always strictly superior.

The one exception is for the output layer because if y is either 0 or 1, then it makes sense for \( \hat{y} \) to be a number, the one to output that's between 0 and 1 rather than between minus 1 and 1.

So the one exception where we would use the sigmoid activation function is when you are using binary classification, in which case you might use the sigmoid activation function for the output layer.

And so what you see in this example is where you might have a tanh activation function for the hidden layer, and sigmoid for the output layer. So activation functions can be different for different layers.

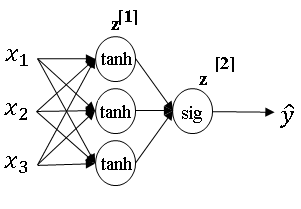
And sometimes to note that activation functions are different for different layers, we might use these square bracket superscripts as well to indicate that \( g^{[1]} \) may be different than \( g^{[2]} \).

Now, one of the downsides of both the sigmoid function and the tanh function is that if z is either very large or very small, then the gradient or the derivative or the slope of this function becomes very small. So if z is very large or z is very small, the slope of the function ends up being close to 0. And so this can slow down gradient descent.

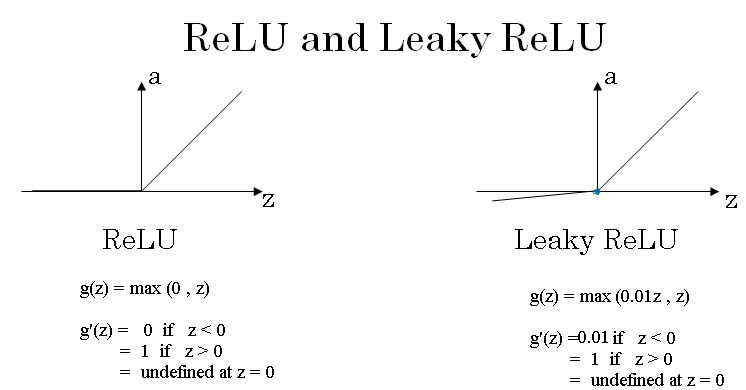
So one other choice that is very popular in machine learning is what's called the rectify linear unit. So the value function looks like this.

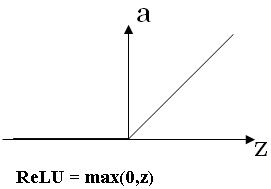
And the formula is a = max(0,z). So the derivative is 1, so long as z is positive. And the derivative or the slope is 0, when z is negative.

If you're implementing this, technically the derivative when z is exactly 0 is not well defined. But when you implement this in the computer, the answer you get exactly is z equals \( \sim 0 \).

If your output is 0, 1 value i.e. if you're using binary classification, then the sigmoid activation function is a very natural choice for the output layer. And then for all other unit's we use ReLU, or the rectified linear unit, Is increasingly the default choice of activation function.

So if you're not sure what to use for your hidden layer, we would just use the ReLU activation function.

One disadvantage of the ReLU is that the derivative is equal to zero, when z is negative. In practice, this works just fine. But there is another version of the ReLU called the leaky ReLU.

I will give you the formula on the next slide. But instead of it being 0 when z is negative, it just takes a slight slope like so, so this is called the leaky ReLU.

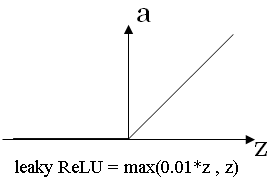
So a common piece of advice would be, if you're not sure which one of these activation functions work best, try them all, and evaluate on a holdout validation set, or a development set, and see which one works better, and then go with that.

And I think that by testing these different choices for your application, you'd be better at future-proofing your neural network architecture against the idiosyncracies of your problem, as well as evolutions of the algorithms.

Rather than if I were to tell you always use a ReLU activation and don't use anything else. That just may or may not apply for whatever problem you end up working on either in the near future or in the distant future.

Why does the neural network need a non-linear activation function? Turns out that your neural network to compute interesting functions, you do need to pick a non-linear activation function.

So, here's the forward propagation equations for the neural network.

If we get rid of the function g? And sets \( a^{[1]} \) equals \( z^{[1]} \). Or alternatively, you can say that \( g^{[1]}(z) \) is equal to z.

This is called the linear activation function or identity activation function because it just outputs whatever was input.

Secondly, if \( a^{[2]} \) was just equal to \( z^{[2]} \) then It turns out this model is just computing \( \hat{y} \) as a linear function of your input features, x.

This is shown as below:
\( a^{[1]} = z^{[1]} = W^{[1]}X + b^{[1]} \\ a^{[2]} = z^{[2]} = W^{[2]}a^{[1]} + b^{[2]} \\ a^{[2]} = z^{[2]} = W^{[2]}(W^{[1]}X + b^{[1]}) + b^{[2]} \\ a^{[2]} = z^{[2]} = (W^{[2]}W^{[1]})X + (W^{[2]}b^{[1]} + b^{[2]}) \\ a^{[2]} = z^{[2]} = W'X + b' \)

In the second step we substitute, the first equation in place of \( a^{[1]}\). Solving further we can show that \( a^{[2]} = z^{[2]} = W'X + b' \) Where W' and b' are the new weights and bias. Thus, the new network is just outputting a linear function of the input.

And we'll talk about deep networks later, neural networks with many, many layers, many hidden layers, and it turns out that.

If you use a linear activation function or alternatively, if you don't have an activation function then no matter how many layers your neural network has, all its doing is just computing a linear activation function. So you might as well not have any hidden layers.

So unless you throw a non-linear there then you're not computing more interesting functions as you go deeper in the network.

When you implement back propagation for your neural network, you need to either compute the slope or the derivative of the activation functions.

So, let's take a look at common choices of activation functions and how you can compute the slope of these functions.

Here's the Sigmoid activation function. If you take the derivative of the Sigmoid function, it is possible to show that it is equal to \( g'(z) = a(1-a) \)

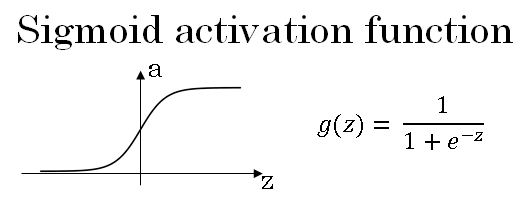
The shorthand for the derivative is \( g'(z) \) also known as g prime of z (the derivative of the function of g with respect to the input variable z).

Let's now look at the Tanh activation function. Similar to what we had previously, the formula for the hyperbolic tangent function is given below.

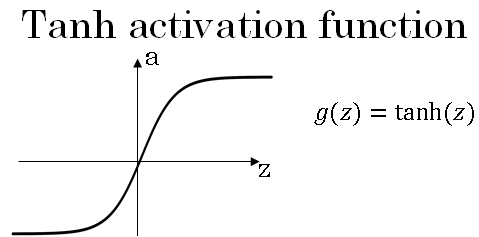
The derivative of this function is given by \( g'(z) = 1 - a^2 \)

Finally, here's how you compute the derivatives for the ReLU and Leaky ReLU activation functions.

With these building blocks it is possible to implement gradient descent in the next steps.