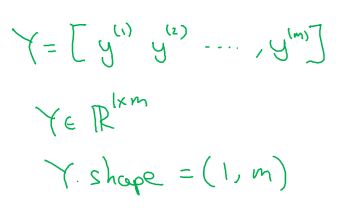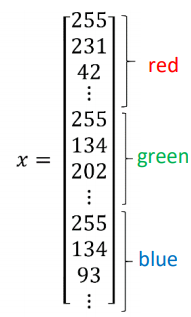
A single training example is represented by a pair, (x,y) where x is an x-dimensional feature vector and y, the label, is either 0 or 1.

Your training sets will comprise lower-case m training examples.

And so your training sets will be written (x⁽¹⁾, y⁽¹⁾) which is the input and output for your first training example (x⁽²⁾, y⁽²⁾) for the second training example up to (x^(m), y^(m)) which is your last training example.

For a test set, we might sometimes use m_test to denote the number of test examples.

Finally, to output all of the training examples into a more compact notation, we're going to define a matrix, X.

As defined by taking you training set inputs (x⁽¹⁾, x⁽²⁾, ... x^(m)) and so on and stacking them in columns. This is shown in the below diagram.

So this matrix X will have M columns, where m is the number of train examples and the number of railroads, or the height of this matrix is n_x.

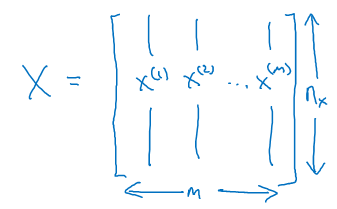
Implementing neural networks using this convention, will make the implementation much easier.

So just to recap, x is a N_x by m dimensional matrix, and when you implement this in Python, you see that x.shape (the python command for finding the shape of the matrix) gives nx, m.

How about the output labels Y? It turns out that to make your implementation of a neural network easier, it would be convenient to also stack Y In columns.

So we're going to define capital Y to be equal to \([Y^{(1)}, Y^{(2)}, ...., Y^{(m)}] \) like so. So Y here will be a 1 by m dimensional matrix.