Lets try to get an intuitive understanding of derivatives we've plotted below the function f(a) = 3a. So it's just a straight line.

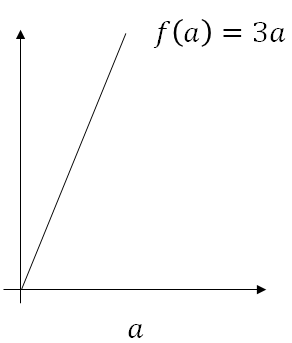
To gain intuition about derivatives let's look at a few points on this function, let's say that 'a' is equal to 2 in that case f(a) = 3a is equal to 6 so if 'a' is equal to 2 then you know f(a) will be equal to three times of 'a' i.e. 6.

Let's say we give the value of 'a' you know just a little bit of a nudge so just bump up 'a' little bit so there is now 2.001, we get a = 2.001. Now f(a) is equal to three times 'a' so f(a)=6.003.

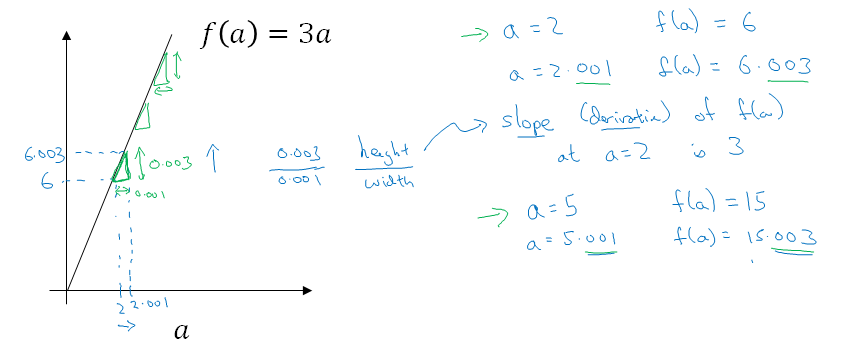
If you look at this green low triangle what we see is that if I move 'a' by 0.001 to the right then f(a) goes up by three times the amount that a went up.

So we're going to say that the slope or the derivative of the function f(a) at 'a' = 3. It is represented as below in the mathematical form:

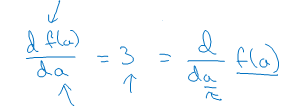
The derivative basically means slope and more formally the slope is defined as the height divided by the width of the little triangle that we have in green so this is you know 0.003 over 0.001 i.e. \( \frac{0.003}{0.001}\). This just represents the fact that when you nudge 'a' to the right by 0.001 or by any tiny amount the amount that f(a) goes up is three times as big.

Mathematically, The derivative of a function describes the function's instantaneous rate of change at a certain point. Another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point.

The given function f(a)=3a has the same slope everywhere and one way to see that is that wherever you draw this your little triangle right the height divided by the width always has a ratio of three to one (In above figure we have also taken a = 5).

However, there are slightly more complex examples where the slopes of the function can be different at different points on the function

You have plotted the function f(a) = a². Let's take a look at the point a=2. So a² is f(a) = 4. The figure of this function is shown below:

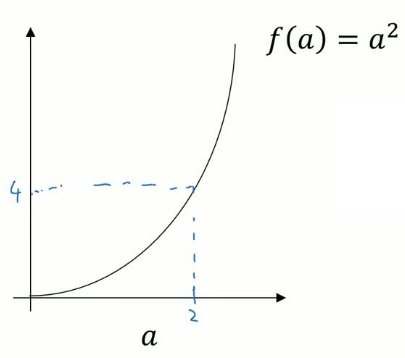
Lets nudge 'a' slightly to the right, so now a=2.001. f(a) which is a² is going to be approximately 4.004. It turns out that the exact value, is actually 4.004001.

So if we draw the point 'a' on the diagram as shown, when 'a' is nudged to the right by 0.001 then f(a) is changed by 0.004. So in the language of calculus, we say that a slope that is the derivative of f(a) at a=2 is 4 or to write this out of our calculus notation, we say that d/da of f(a) = 4 when a=2.

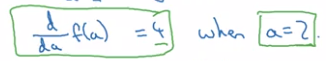
Now one thing about this function f(a) = a² is that the slope is different for different values of a.

So let's look at a different point. If a=5, so instead of a=2, and now a=5 then a²=25, so that's f(a). If I nudge '8 'a' to the right again, it's tiny little nudge to '8'a', so now a=5.001 then f(a) will be approximately 25.010. So what we see is that by nudging a up by .001, f(a) goes up ten times as much.

So we have that \( \frac{d f(a)}{da} \) = 10 when a=5 because f(a) goes up ten times as much as a does when I make a tiny little nudge to 'a'.

So one way to see why the derivatives is different at different points is that if you draw that little triangle right at different locations on this, you'll see that the ratio of the height of the triangle over the width of the triangle is very different at different points on the curve.

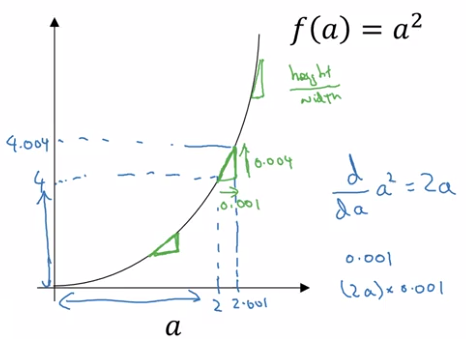
So here, the slope=4 when a=2, a=10, when a=5. Now if you pull up a calculus textbook, a calculus textbook will tell you that \( \frac{d f(a)}{da} \), so f(a) = a², so that's \( \frac{d f(a)}{da} \) of a². One of the formulas you find are the calculus textbook is that this thing, the slope of the function a²=2a.

And indeed, this is consistent with what we've worked out. Namely, when a=2, the slope of function to a is 2x2=4. And when a=5 then the slope of the function 2xa is 2x5=10.

Let's just go through a few more quick examples. If f(a) = a³ you see that the slope of this function, again, the derivative of this function is equal to 3a².

So the way to interpret this is as follows. Let's take a=2 as an example again. So f(a) or a³ = 8. So we give a a tiny little nudge, you find that f(a) is about 8.012. Below examples are of other functions and their derivatives.

So, from the above examples we conclude that the slope or the derivative can be different at different points on the curve.