You've seen by now that training neural nets can involve setting a lot of different hyperparameters.

Now, how do you go about finding a good setting for these hyperparameters? In this section, I want to share with you some guidelines, some tips for how to systematically organize your hyperparameter tuning process, which hopefully will make it more efficient for you to converge on a good setting of the hyperparameters.

One of the painful things about training deep neural networks is the sheer number of hyperparameters you have to deal with, ranging from the learning rate alpha \( \alpha \) to the momentum term beta \( \beta \), if using momentum, or the hyperparameters for the Adam Optimization Algorithm which are \( \beta_1 \), \( \beta_2 \), and \( \epsilon \).

Maybe you have to pick the number of layers, maybe you have to pick the number of hidden units for the different layers, and maybe you want to use learning rate decay, so you don't just use a single learning rate alpha.

And then of course, you might need to choose the mini-batch size.

So it turns out, some of these hyperparameters are more important than others.

For most learning applications I would say, alpha, the learning rate is the most important hyperparameter to tune.

Other than alpha, a few other hyperparameters I tend to would maybe tune next, would be maybe the momentum term, say, 0.9 is a good default.

I'd also tune the mini-batch size to make sure that the optimization algorithm is running efficiently.

Often I also fiddle around with the hidden units.

Of the ones I've circled in orange, these are really the three that I would consider second in importance to the learning rate alpha and then third in importance after fiddling around with the others, the number of layers can sometimes make a huge difference, and so can learning rate decay.

And then when using the Adam algorithm I actually pretty much never tuned \( \beta_1 \), \( \beta_2 \), and \( \epsilon \). Pretty much I always use 0.9, 0.999 and 10^-8 although you can try tuning those as well if you wish.

So the chronological order of importance for hyper-parameters: \( \alpha \\ \beta \\ \beta_1 , \beta_2 , \epsilon \\ \text{Number of hidden layers} \\ \text{Number of hidden units} \\ \text{learning rate decay} \\ \text{Mini batch size} \\ \)

Now, if you're trying to tune some set of hyperparameters, how do you select a set of values to explore?

In earlier generations of machine learning algorithms, if you had two hyperparameters, which we are calling hyperparameter one and hyperparameter two , it was common practice to sample the points in a grid like so and systematically explore these values.

By placing down a five by five grid as shown below. In practice, it could be more or less than the five by five grid but you try out in this example all 25 points and then pick whichever hyperparameter works best.

And this practice works okay when the number of hyperparameters was relatively small.

In deep learning, what we tend to do, and what I recommend you do instead, is choose the points at random.

So we randomly choose 25 points and then try out the hyperparameters on this randomly chosen set of points. And the reason you do that is that it's difficult to know in advance which hyperparameters are going to be the most important for your problem.

As given in the chronology some hyperparameters are actually much more important than others. So to take an example, let's say hyperparameter one turns out to be alpha, the learning rate.

And to take an extreme example, let's say that hyperparameter two was that value epsilon that you have in the denominator of the Adam algorithm.

So your choice of alpha matters a lot and your choice of epsilon hardly matters. So if you sample in the grid then you've really tried out five values of alpha and you might find that all of the different values of epsilon give you essentially the same answer.

So you've now trained 25 models and only got into trial five values for the learning rate alpha, which I think is really important. Whereas in contrast, if you were to sample at random, then you will have tried out 25 distinct values of the learning rate alpha and therefore you be more likely to find a value that works really well.

I've explained this example, using just two hyperparameters. In practice, you might be searching over many more hyperparameters than these, so if you have, say, three hyperparameters, I guess instead of searching over a square, you're searching over a cube where this third dimension is hyperparameter three and then by sampling within this three-dimensional cube you get to try out a lot more values of each of your three hyperparameters.

And in practice you might be searching over even more hyperparameters than three and sometimes it's just hard to know in advance which ones turn out to be the really important hyperparameters for your application and sampling at random rather than in the grid shows that you are more richly exploring set of possible values for the most important hyperparameters, whatever they turn out to be.

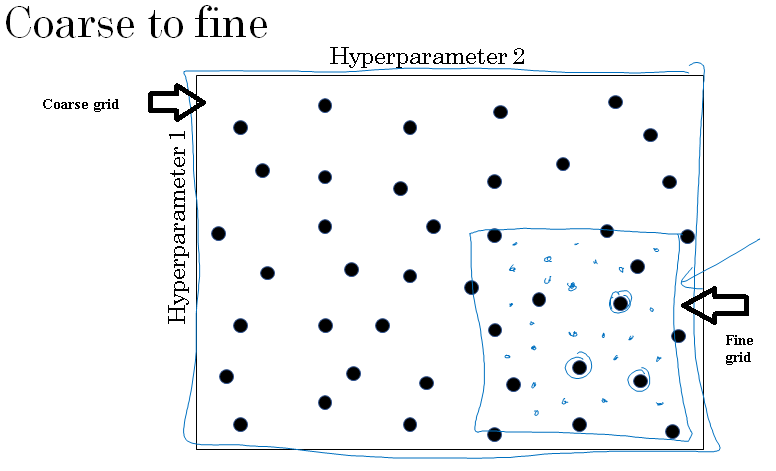
When you sample hyperparameters, another common practice is to use a coarse to fine sampling scheme.

So let's say in this two-dimensional example that you sample points, and maybe you found that this point work the best and maybe a few other points around it tended to work really well, then in the course of the final scheme what you might do is zoom in to a smaller region of the hyperparameters and then sample more density within this space.

Or maybe again at random, but to then focus more resources on searching within the blue square given below if you're suspecting that the best setting, the hyperparameters, may be in this region.

So after doing a coarse sample of this entire square, that tells you to then focus on a smaller square.

You can then sample more densely into smaller square. So this type of a coarse to fine search is also frequently used. And by trying out these different values of the hyperparameters you can then pick whatever value allows you to do best on your training set objective or does best on your development set or whatever you're trying to optimize in your hyperparameter search process.

So I hope this gives you a way to more systematically organize your hyperparameter search process.

The two key takeaways are, use random sampling and adequate search and optionally consider implementing a coarse to fine search process.

But there's even more to hyperparameter search than this. Let's see more in the next section about how to choose the right scale on which to sample your hyperparameters.