Why does regularization help with overfitting? Why does it help with reducing variance problems?

Let's go through the example below to gain some intuition about how it works. Recall that high bias, high variance and that looks something like the image given below.

Also given a large and deep neural network.

For this network we have a cost function like J which looks like the equation given below:

\( J( w^{[1]}, b^{[1]} , .... , w^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)} , y^{(i)}) \)

So what we did for regularization was add this extra term that penalizes the weight matrices from being too large. This term is known as the Frobenius norm (||w^{[l]}||^2_F = \sum_{i=1}^{n^{[l]}} \sum_{i=1}^{n^{[l-1]}} (w_{ij}^{[l]})^2). The final result is given below:

\( J( w^{[1]}, b^{[1]} , .... , w^{[L]}, b^{[L]}) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)} , y^{(i)}) + ( \frac{\lambda}{m} W^{[2]} ) \)

So why is it that shrinking the L2 norm or the Frobenius norm or the parameters might cause less overfitting?

One intuition is that if you set regularisation parameter - lambda to be big, gradient descent will be really incentivized to set the weight matrices W to be reasonably close to zero.

So one piece of intuition is maybe it set the weight to be so close to zero for a lot of hidden units that's basically zeroing out a lot of the impact of these hidden units.

And if that's the case, then this much simplified neural network becomes a much smaller neural network as given in figure below.

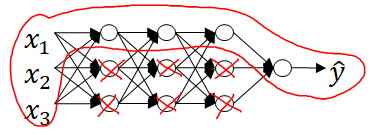
And so that will take you from this overfitting case much closer to the high bias case.

But hopefully there'll be an intermediate value of lambda that results in a result closer to the just right case.

The intuition of completely zeroing out of a bunch of hidden units isn't quite right. It turns out that what actually happens is they'll still use all the hidden units, but each of them would just have a much smaller effect.

But you do end up with a simpler network and as if you have a smaller network that is therefore less prone to overfitting.