First we need to choose the individuals from the population that will be included in the sample. Then, once we have chosen the individuals, we need to collect data from them. The first stage is called sampling, and the second stage is called study design.

As we have seen, exploratory data analysis seeks to illuminate patterns in the data by summarizing the distributions of quantitative or categorical variables, or the relationships between variables.

In the final part of the course, statistical inference, we will use the summaries about variables or relationships that were obtained in the study to draw conclusions about what is true for the entire population from which the sample was chosen.

For this process to "work" reliably, it is essential that the sample be truly representative of the larger population. For example, if researchers want to determine whether the antidepressant Zoloft is effective for teenagers in general, then it would not be a good idea to only test it on a sample of teens who have been admitted to a psychiatric hospital, because their depression may be more severe, and less treatable, than that of teens in general.

Thus, the very first stage in data production, sampling, must be carried out in such a way that the sample really does represent the population of interest.

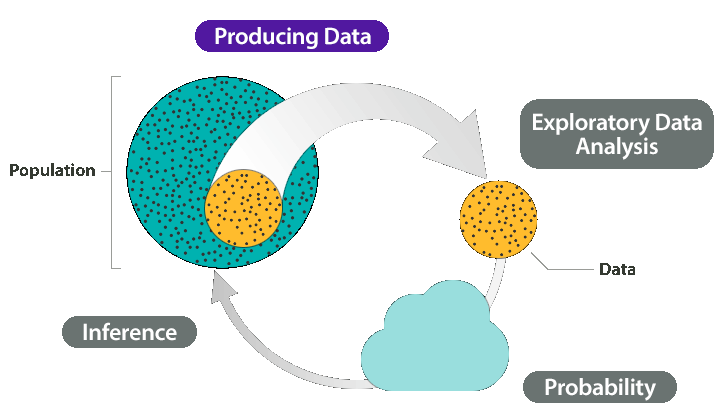
Choosing a sample is only the first stage in producing data, so it is not enough to just make sure that the sample is representative.

We must also remember that our summaries of variables and their relationships are only valid if these have been assessed properly. For instance, if researchers want to test the effectiveness of Zoloft versus Prozac for treating teenagers, it would not be a good idea to simply compare levels of depression for a group of teenagers who happen to be using Zoloft to levels of depression for a group of teenagers who happen to be using Prozac.

If they discover that one group of patients turns out to be less depressed, it could just be that teenagers with less serious depression are more likely to be prescribed one of the drugs over the other.

In situations like this, the design for producing data must be considered carefully. Studies should be designed to discover what we want to know about the variables of interest for the individuals in the sample.

In particular, if what you want to know about the variables is whether there is a causal relationship between them, special care should be given to the design of the study (since, as we know, association does not imply causation).

In this unit, we will focus on these two stages of data production: obtaining a sample, and designing a study.

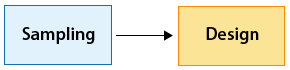
The two stages of data production. Sampling occurs, then Design occurs. Throughout this section, we establish guidelines for the ideal production of data.

While we will hold these guidelines as standards to strive for, realistically it is rarely possible to carry out a study that is completely free of flaws.

Common sense must frequently be applied in order to decide which imperfections we can live with and which ones could completely undermine a study's results.

A sample that produces data that is not representative because of the systematic under- or over-estimation of the values of the variable of interest is called biased. Bias may result from either a poor sampling plan or from a poor design for evaluating the variable of interest.

Example: #1 Suppose you want to determine the musical preferences of all students at your university, based on a sample of students. Here are some examples of the many possible ways to pursue this problem.

Post a music-lovers' survey on a university Internet bulletin board, asking students to vote for their favorite type of music.

This is an example of a volunteer sample, where individuals have selected themselves to be included. Such a sample is almost guaranteed to be biased. In general, volunteer samples tend to be comprised of individuals who have a particularly strong opinion about an issue, and are looking for an opportunity to voice it. Whether the variable's values obtained from such a sample are over- or under-stated, and to what extent, cannot be determined. As a result, data obtained from a voluntary response sample is quite useless when you think about the "Big Picture," since the sampled individuals only provide information about themselves, and we cannot generalize to any larger group at all.

NOTE... It should be mentioned that in some cases volunteer samples are the only ethical way to obtain a sample. In medical studies, for example, in which new treatments are tested, subjects must choose to participate by signing a consent form that highlights the potential risks and benefits. As we will discuss in the next module, a volunteer sample is not so problematic in a study conducted for the purpose of comparing several treatments.

Example: #2 Stand outside the Student Union, across from the Fine Arts Building, and ask students passing by to respond to your question about musical preference.

This is an example of a convenience sample, where individuals happen to be at the right time and place to suit the schedule of the researcher. Depending on what variable is being studied, it may be that a convenience sample provides a fairly representative group. However, there are often subtle reasons why the sample's results are biased. In this case, the proximity to the Fine Arts Building might result in a disproportionate number of students favoring classical music. A convenience sample may also be susceptible to bias because certain types of individuals are more likely to be selected than others. In the extreme, some convenience samples are designed in such a way that certain individuals have no chance at all of being selected, as in the next example.

Example: #3 Ask your professors for email rosters of all the students in your classes. Randomly sample some addresses, and email those students with your question about musical preference.

Here is a case where the sampling frame—list of potential individuals to be sampled—does not match the population of interest. The population of interest consists of all students at the university, whereas the sampling frame consists of only your classmates. There may be bias arising because of this discrepancy. For example, students with similar majors will tend to take the same classes as you, and their musical preferences may also be somewhat different from those of the general population of students. It is always best to have the sampling frame match the population as closely as possible.

Example: #4 Obtain a student directory with email addresses of all the university's students, and send the music poll to every 50th name on the list.

This is called systematic sampling. It may not be subject to any clear bias, but it would not be as safe as taking a random sample.

If individuals are sampled completely at random, and without replacement, then each group of a given size is just as likely to be selected as all the other groups of that size. This is called a simple random sample (SRS). In contrast, a systematic sample would not allow for sibling students to be selected, because of having the same last name. In a simple random sample, sibling students would have just as much of a chance of both being selected as any other pair of students. Therefore, there may be subtle sources of bias in using a systematic sampling plan.

Example: #5 Obtain a student directory with email addresses of all the university's students, and send your music poll to a simple random sample of students. As long as all of the students respond, then the sample is not subject to any bias, and should succeed in being representative of the population of interest.

But what if only 40% of those selected email you back with their vote?

The results of this poll would not necessarily be representative of the population, because of the potential problems associated with volunteer response. Since individuals are not compelled to respond, often a relatively small subset take the trouble to participate. Volunteer response is not as problematic as a volunteer sample (presented in example 1 above), but there is still a danger that those who do respond are different from those who don't, with respect to the variable of interest. An improvement would be to follow up with a second email, asking politely for students' cooperation. This may boost the response rate, resulting in a sample that is fairly representative of the entire population of interest, and it may be the best that you can do, under the circumstances. Nonresponse is still an issue, but at least you have managed to reduce its impact on your results.

A simple random sample is the easiest way to base a selection on randomness. There are other, more sophisticated, sampling techniques that utilize randomness that are often preferable in real-life circumstances. Any plan that relies on random selection is called a probability sampling plan (or technique). The following three probability sampling plans are among the most commonly used:

Simple Random Sampling is, as the name suggests, the simplest probability sampling plan. It is equivalent to “selecting names out of a hat.” Each individual as the same chance of being selected.

Cluster Sampling—This sampling technique is used when our population is naturally divided into groups (which we call clusters). For example, all the students in a university are divided into majors; all the nurses in a certain city are divided into hospitals; all registered voters are divided into precincts (election districts). In cluster sampling, we take a random sample of clusters, and use all the individuals within the selected clusters as our sample. For example, in order to get a sample of high-school seniors from a certain city, you choose 3 high schools at random from among all the high schools in that city, and use all the high school seniors in the three selected high schools as your sample.

Stratified Sampling—Stratified sampling is used when our population is naturally divided into sub-populations, which we call stratum (plural: strata). For example, all the students in a certain college are divided by gender or by year in college; all the registered voters in a certain city are divided by race. In stratified sampling, we choose a simple random sample from each stratum, and our sample consists of all these simple random samples put together. For example, in order to get a random sample of high-school seniors from a certain city, we choose a random sample of 25 seniors from each of the high schools in that city. Our sample consists of all these samples put together.

Each of those probability sampling plans, if applied correctly, are not subject to any bias, and thus produce samples that represent well the population from which they were drawn.

Comment: Cluster vs. Stratified

Students sometimes get confused about the difference between cluster sampling and stratified sampling. Even though both methods start out with the population somehow divided into groups, the two methods are very different.

In cluster sampling, we take a random sample of whole groups of individuals, while in stratified sampling we take a simple random sample from each group. For example, say we want to conduct a study on the sleeping habits of undergraduate students at a certain university, and need to obtain a sample. The students are naturally divided by majors, and let's say that in this university there are 40 different majors.

In cluster sampling, we would randomly choose, say, 5 majors (groups) out of the 40, and use all the students in these five majors as our sample. In stratified sampling, we would obtain a random sample of, say, 10 students from each of the 40 majors (groups), and use the 400 chosen students as the sample. Clearly in this example, stratified sampling is much better, since the major of the student might have an effect on the student's sleeping habits, and so we would like to make sure that we have representatives from all the different majors. We’ll stress this point again following the example and activity.

Example Suppose you would like to study the job satisfaction of hospital nurses in a certain city based on a sample. Besides taking a simple random sample, here are two additional ways to obtain such a sample.

1. Suppose that the city has 10 hospitals. Choose one of the 10 hospitals at random and interview all the nurses in that hospital regarding their job satisfaction. This is an example of cluster sampling, in which the hospitals are the clusters.

2. Choose a random sample of 50 nurses from each of the 10 hospitals and interview these 50 * 10 = 500 regarding their job satisfaction. This is an example of stratified sampling, in which each hospital is a stratum.

What sampling technique is being used in this scenario? Voters are selected at random from an alphabetical list of all registered voters.

Answer : simple random sampling; Voters were selected directly from a list of the entire population (all registered voters).

What sampling technique is being used in this scenario? Voters are selected by choosing at random several of the city's zip codes and selecting all the voters from those selected zip codes.

Answer : cluster sampling. The population of registered voters was divided into groups (zip codes). A number of those groups were chosen, and then all members of each chosen group were selected to participate in the study.

What sampling technique is being used in this scenario? Several pieces of fruit from each tree in an orchard are selected.

Answer : stratified sampling The population was divided into groups (trees), then some fruit from each group was selected. Since we do not know if all of the trees contain the same kind of fruit, one way to ensure that we will have a representative sample of fruit is to select some from each tree. Note: Suppose the trees are lemon, lime, orange, and tangerine. One technique would be first to stratify the orchard by type of trees (according to the kind of fruit it has), then select some of each type of tree. This would be a multistage sample, using strata first, and then clusters second.

Cluster or Stratified—which one is better?

Let’s go back and revisit the job satisfaction of hospital nurses example and discuss the pros and cons of the two sampling plans that are presented. Certainly, it will be much easier to conduct the study using the cluster sample, since all interviews are conducted in one hospital as opposed to the stratified sample, in which the interviews need to be conducted in 10 different hospitals. However, the hospital that a nurse works in probably has a direct impact on his/her job satisfaction, and in that sense, getting data from just one hospital might provide biased results. In this case, it will be very important to have representation from all the city hospitals, and therefore the stratified sample is definitely preferable. On the other hand, say that instead of job satisfaction, our study focuses on the age or weight of hospital nurses.

In this case, it is probably not as crucial to get representation from the different hospitals, and therefore the more easily obtained cluster sample might be preferable.

Comment: Another commonly used sampling technique is multistage sampling, which is essentially a “complex form” of cluster sampling. When conducting cluster sampling, it might be unrealistic, or too expensive to sample all the individuals in the chosen clusters. In cases like this, it would make sense to have another stage of sampling, in which you choose a sample from each of the randomly selected clusters, hence the term multistage sampling.

For example, say you would like to study the exercise habits of college students in the state of California. You might choose 8 colleges (clusters) at random, but you are certainly not going to use all the students in these 8 colleges as your sample. It is simply not realistic to conduct your study that way. Instead you move on to stage 2 of your sampling plan, in which you choose a random sample of 100 males and a random sample of 100 females from each of the 8 colleges you selected in stage 1.

So in total you have 8 * (100+100) = 1,600 college students in your sample.

In this case, stage 1 was a cluster sample of 8 colleges and stage 2 was a stratified sample within each college where the stratum was gender.

Multistage sampling can have more than 2 stages. For example, to obtain a random sample of physicians in the United States, you choose 10 states at random (stage 1, cluster). From each state you choose at random 8 hospitals (stage 2, cluster). Finally, from each hospital, you choose 5 physicians from each sub-specialty (stage 3, stratified).