Introduction to Probability
The four-step process that encompasses statistics - Producing data—how data are obtained and what considerations affect the data production process. Exploratory data analysis —tools that help us get a first feel for the data, by exposing their features using graphs and numbers.
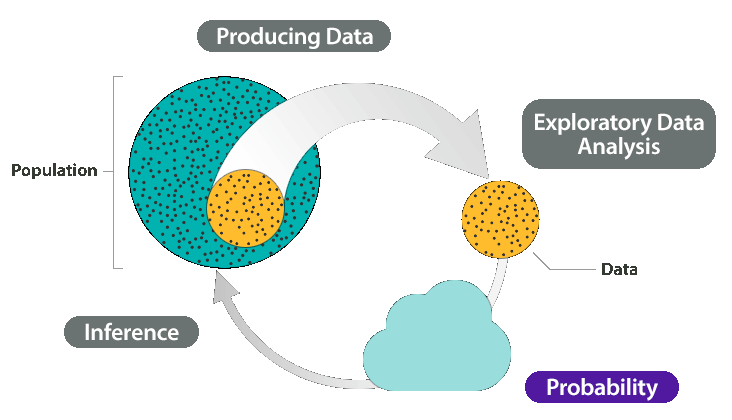
Our eventual goal is inference—drawing reliable conclusions about the population based on what we've discovered in our sample. In order to really understand how inference works, though, we first need to talk about probability, because it is the underlying foundation for the methods of statistical inference. We use an example to explain why probability is so essential to inference.
First, As we all know, the way statistics works is that we use a sample to learn about the population from which it was drawn. Ideally, the sample should be random so that it represents the population well.
Recall from the Sampling section that when we say a random sample represents the population well, we mean that there is no inherent bias in this sampling technique.
It is important to acknowledge, though, that this does not mean that all random samples are necessarily “perfect.” Random samples are still random, and therefore no random sample will be exactly the same as another. One random sample may give a fairly accurate representation of the population, while another random sample might be “off,” purely due to chance.
Unfortunately, when looking at a particular sample (which is what happens in practice), we will never know how much it differs from the population.
This uncertainty is where probability comes into the picture. We use probability to quantify how much we expect random samples to vary.
This gives us a way to draw conclusions about the population in the face of the uncertainty that is generated by the use of a random sample. The following example will illustrate this important point.
Example: Death Penalty
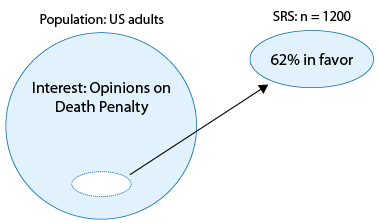
Suppose that we are interested in estimating the percentage of U.S. adults who favor the death penalty. In order to do so, we choose a random sample of 1,200 U.S. adults and ask their opinion: either in favor of or against the death penalty. We find that 744 out of the 1,200, or 62%, are in favor.
We have a large circle representing the entire population of US Adults. We are interested in the population's opinions on the death penalty. From this population we take out a random sample of 1200 adults, and find that within this sample, 62% are in favor of the death penalty.
Our goal here is to do inference—learn and draw conclusions about the opinions of the entire population of U.S. adults regarding the death penalty, based on the opinions of only 1,200 of them.
Can we conclude that 62% of the population favors the death penalty? Another random sample could give a very different result. So we are uncertain. But since our sample is random, we know that our uncertainty is due to chance, and not due to problems with how the sample was collected.
So we can use probability to describe the likelihood that our sample is within a desired level of accuracy. For example, probability can answer the question, "How likely is it that our sample estimate is no more than 3% from the true percentage of all U.S. adults who are in favor of the death penalty?”
The answer to this question (which we find using probability) is obviously going to have an important impact on the confidence we can attach to the inference step. In particular, if we find it quite unlikely that the sample percentage will be very different from the population percentage, then we have a lot of confidence that we can draw conclusions about the population based on the sample.
Introduction to Probability - Lets make a deal Paradox
In a popular game show, contestants are asked to choose one of three doors. Behind one is a fabulous prize! Behind the others are gag gifts. When you choose a door, the game show host shows you a gag gift behind one of the two doors not chosen. You are given the option of switching to the one remaining door or staying with your original choice. Which is the better strategy: switch or stay?
The intuition of most people is that each of the two doors is equally likely to contain the prize—that there is a 50-50 chance of winning with either selection. This, however, is not the case. Actually, there is a 67% chance—or a probability of 2/3 (2 out of 3)—of winning by switching, and only a 33% chance—or a probability of 1/3 (1 out of 3)—of winning by staying with the door that was originally chosen.
Initially when you're asked to choose a door, each one of the three doors is equally likely to have the prize behind it with probability one-third.
Let's say you choose door A. Now let's divide the three doors into two groups.
There is a probability of one-third that the prize is behind the door that you chose, A, and a probability of two-thirds that the prize is behind one of the other unchosen doors, B or C.
Say that now the host is revealing door C which has no prize behind it.
You now have the choice between staying with the door A which you initially chose or switching to door B.
Now that door C has been revealed, there is zero chance that it hides the prize and therefore the entire probability of two-thirds that was equally divided between doors B and C before is now all attached to door B.
Note that there is still one-third chance that the prize is behind door A but there is two-thirds chance that the prize is behind door B and therefore it's better to switch.
Second explanation :
When you, the contestant, start the game there are three possible cases. The prize, indicated by the dollar sign, is either behind door C, behind door B, or behind door A.
Since you obviously have no idea which of the three cases you're faced with, you choose one of the three doors at random.
Say you choose door A. If you're in case one where you chose door A and the prize is behind door C, the host will obviously reveal the empty door B to you in which case in order to win you need to switch from door A to door C.
If you're in case two, where you chose door A and the prize is behind door B the host will obviously reveal the empty door C to you in which case in order to win you need to switch from door A to door C.
And finally, if you're in case three, where you chose door A and the prize is behind door A, the host can reveal either one of the remaining empty doors. Say that the host reveals door B.
Note that this is the only case out of the three in which in order to win you should stay with the door you initially chose. Let's summarize.
There are three possible cases in the game. We saw that in two of the three cases if you switch you win and only in one of the three if you stay you win.
Since you have no idea which of the three cases you're faced with, you might as well go with the switching strategy because in two out of the possible three cases it will lead you to winning.
Introduction to Probability
Probability is a mathematical description of randomness and uncertainty. It is a way to measure or quantify uncertainty. Another way to think about probability is that it is the official name for "chance."
Probability is used to answer the following types of questions:
What is the chance that it will rain tomorrow?
What is the chance that a stock will go up in price?
What is the chance that I will have a heart attack?
What is the chance that I will live longer than 70 years?
What is the likelihood that when rolling a pair of dice, I will roll doubles?
What is the probability that I will win the lottery?
Each of these examples has some uncertainty. For some, the chances are quite good, so the probability would be quite high. For others, the chances are not very good, so the probability is quite low (especially winning the lottery).
Certainly, the chance of rain is different each day, and is higher during some seasons. Your chance of having a heart attack, or of living longer than 70 years, depends on things like your current age, your family history, and your lifestyle. However, you could use your intuition to predict some of those probabilities fairly accurately, while others you might have no hunches about at all.
Notation We think you will agree that the word probability is a bit long to include in equations, graphs and charts, so it is customary to use some simplified notation instead of the entire word.
If we wish to indicate "the probability it will rain tomorrow," we use the notation "P(rain tomorrow)." We can abbreviate the probability of anything. If we let A represent what we wish to find the probability of, then P(A) would represent that probability.
We can think of "A" as an "event."
NOTATION MEANING P(win lottery) the probability that a person who has a lottery ticket will win that lottery P(A) the probability that event A will occur P(B) the probability that event B will occur Principle : The "probability" of an event tells us how likely it is that the event will occur.
What values can the probability of an event take, and what does the value tell us about the likelihood of the event occurring?
The probability of any event ranges from zero to one. Let's start with the extremes: zero and one.
The probability of zero means that the event has zero chance of happening. It will never occur.
An event has probability one if it will occur for certain. In the middle, a probability of one-half indicates that the event has 50% chance of happening.
In other words, the event is as likely to occur as it is not to occur.
Any probability that is greater than one-half indicates that the event is more likely to occur that it is not to occur.
And a probability that is below one-half indicates that the event is more likely not to occur than it is to occur.
Principle : The probability that an event will occur is between 0 and 1 or 0 ≤ P(A) ≤ 1.
Many people prefer to express probability in percentages. Since all probabilities are decimals, each can be changed to an equivalent percentage. Thus, the latest principle is equivalent to saying, "The chance that an event will occur is between 0% and 100%."
Probabilities can be determined in two fundamental ways. Keep reading to find out what they are.
- Explanation :
impossible event has zero probability
- Explanation :
A probability of 1 represents an event that will occur for certain.
- Explanation :
A probability of 0.60 represents an event that will occur more often than not. Specifically, it will occur almost two-thirds (0.67) of the time.
Let's Summarize
Probability is a way of quantifying uncertainty.
We are interested in the probability of an event—the likelihood of the event occurring.
The probability of an event ranges from 0 to 1. The closer the probability is to 0, the less likely the event is to occur. The closer the probability is to 1, the more likely the event is to occur.
There are two ways to determine probability: Theoretical (Classical) and Empirical (Observational). If we toss a coin, roll a die, or spin a spinner many times, we hardly ever achieve the exact theoretical probabilities that we know we should get, but we can get pretty close. When we run a simulation or when we use a random sample and record the results, we are using empirical probability. This is often called the Relative Frequency definition of probability
Theoretical methods use the nature of the situation to determine probabilities.
Empirical methods use a series of trials that produce outcomes that cannot be predicted in advance (hence the uncertainty).