Rule 4: The Addition Rule for Disjoint Events The Addition Rule for Disjoint Events: If A and B are disjoint events, then P(A or B) = P(A) + P(B).

When dealing with probabilities, the word "or" will always be associated with the operation of addition; hence the name of this rule, "The Addition Rule."

Blood Type O A B AB

Probability 0.44 0.42 0.10 0.04

Here is some additional information:

* A person with type A can donate blood to a person with type A or AB.

* A person with type B can donate blood to a person with type B or AB.

* A person with type AB can donate blood to a person with type AB only.

* A person with type O blood can donate to anyone.

What is the probability that a randomly chosen person is a potential donor for a person with blood type A?

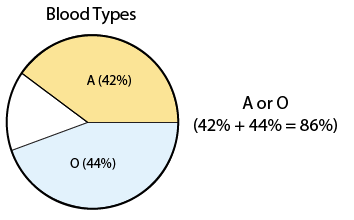
From the information given, we know that being a potential donor for a person with blood type A means having blood type A or O. We therefore need to find P(A or O). Since the events A and O are disjoint, we can use the addition rule for disjoint events to get: P(A or O) = P(A) + P(O) = 0.42 + 0.44 = 0.86. It is easy to see why adding the probability actually makes sense.

If 42% of the population has blood type A and 44% of the population has blood type O, then 42% + 44% = 86% of the population has either blood type A or O, and thus are potential donors to a person with blood type A. This reasoning about why the addition rule makes sense can be visualized using the pie chart below:

The probabilities in this table were calculated from data describing the highest level of educational attainment in 2005 for U.S. adults 25 years old or older. (Source: U.S. Census Bureau, Current Population Survey, March 2005)

Highest Level of Education Attained	Probability
Below high school	0.063
Some high school	0.085
High school degree	0.322
Some college	0.168
College degree	0.181
Graduate or professional degree	0.095

What is the probability that a randomly selected U.S. adult in this age category has not graduated from high school?

It is impossible to tell since the events “no high school” and “some high school” are not disjoint.

0.148

Explanation :

P(has not graduated from high school) = P(“no high school” or “some high school”) = 0.063 + 0.085 
= 0.148. We can add these probabilities since the events “no high school” and “some high school” are disjoint. These events are disjoint because 
the table describes the highest level of educational attainment for an individual.

Blood Type O A B AB

Probability 0.44 0.42 0.10 0.04

A person with type A can donate blood to a person with type A or AB.

A person with type B can donate blood to a person with type B or AB.

A person with type AB can donate blood to a person with type AB only.

A person with type O blood can donate to anyone.

Suppose that there are two patients who are each in need of a blood donation. Patient 1 has blood type A and patient 2 has blood type B. Consider the following events:

D1—a randomly chosen person can be a donor for patient 1.

D2—a randomly chosen person can be a donor for patient 2.

Find P(D1) and P(D2). Write your answers in the text box below.

To be a potential donor for patient 1, who has blood type A, a person must have blood type A or O. Therefore:

P(D1) = P(A or O) = P(A) + P(O) = 0.42 + 0.44 = 0.86.

Note that in this case we can safely use the addition rule for disjoint events since the events A and O are disjoint because we are presuming that a person cannot have more than one blood type.

Similarly, to be a potential donor for patient 2, who has blood type B, a person must have blood type B or O. Therefore:

P(D2) = P(B) + P(O) = 0.10 + 0.44 = 0.54.

Are events D1 and D2 disjoint or overlapping?

Events D1 and D2 are not disjoint, they are overlapping, sharing the outcome O. In other words, D1 and D2 can occur at the same time if a donor has blood type O. Click here to see a visual representation.

Try to (wrongly) apply the addition rule for disjoint events to P(D1 or D2), and explain why the answer you got proves that the addition rule for disjoint events does not work in cases in which the events are not disjoint.

If we wrongly apply the addition rule for disjoint events in order to find P(D1 or D2) we'll get:

P(D1 or D2) = P(D1) + P(D2) = 0.86 + 0.54 = 1.4

The answer is wrong for certain, since we got a probability that is greater than 1. This proves the danger of incorrectly applying the addition rule for disjoint events when it is not appropriate to do so.

The Addition Rule for Disjoint Events can naturally be extended to more than two disjoint events. Let's take three, for example. If A, B and C are three disjoint events, then P(A or B or C) = P(A) + P(B) + P(C). The rule is the same for any number of disjoint events.

Color Percent

Silver 20.2%

White 18.4%

Black 11.6%

Med/Dark Gray 11.5%

Light Brown 8.8%

Med/Dark Blue 8.5%

Medium Red 6.9%

Med/Dark Green 5.3%

Bright Red 3.8%

Dark Red 0.9%

The probabilities in this table were calculated from data describing North America’s favorite car colors in 2003. What is the probability that a randomly chosen car will have one of the three most popular colors?

P(among the top three favorite colors) = P(Silver or White or Black).

Since the three events, Silver, White and Black, are disjoint (since for the purposes of our example a car can have just one color), we can apply the Addition Rule for Disjoint Events (extended to three disjoint events) and get:

P(among the top three colors) = P(Silver) + P(White) + P(Black) = 0.202 + 0.184 + 0.116 = 0.502.

In other words, of the top 10 favorite car colors in the country, the three most popular colors comprised 50.2%.

Rule 5 : P(A and B) = P(event A occurs and event B occurs)

For example, we might be interested in the probability that if two people are chosen at random, both the first has blood type O and the second has blood type O. Since a person with blood type O can donate blood to anyone, this probability might be of particular interest in this context.

So, if events A and B are disjoint, then (by definition) P(A and B)= 0. But what if the events are not disjoint?

Recall that rule 4, the Addition Rule, has two versions. One is restricted to disjoint events, which we've already covered, and we'll deal with the more general version later in this module. The same is true of rule 5. Rule 5 has two versions. The version we'll present here is restricted to a special case that we'll now discuss, and there is a more general version that we'll present in the next module.

The version of rule 5 that will be presented here applies to the special case in which the two events are independent of each other.

independent (definition) Two events A and B are said to be independent if the fact that one event has occurred does not affect the probability that the other event will occur. If whether or not one event occurs does affect the probability that the other event will occur, then the two events are said to be dependent.

A woman's pocket contains two quarters and two nickels. She randomly extracts one of the coins and, after looking at it, replaces it before picking a second coin. Let Q1 be the event that the first coin is a quarter and Q2 be the event that the second coin is a quarter. Are Q1 and Q2 independent events? Yes. Why?

Since the first coin that was selected is replaced, whether or not Q1 occurred (i.e., whether the first coin was a quarter) has no effect on the probability that the second coin will be a quarter, P(Q2).

In either case (whether Q1 occurred or not), when she is selecting the second coin, she has in her pocketand therefore the P(Q2) = 2/4 = 1/2 regardless of whether Q1 occurred.

A woman's pocket contains two quarters and two nickels. She randomly extracts one of the coins, and without placing it back into her pocket, she picks a second coin. As before, let Q1 be the event that the first coin is a quarter, and Q2 be the event that the second coin is a quarter. Are Q1 and Q2 independent events? No. Q1 and Q2 are not independent. They are dependent. Why?

Since the first coin that was selected is not replaced, whether Q1 occurred (i.e., whether the first coin was a quarter) does affect the probability that the second coin is a quarter, P(Q2).

If Q1 occurred (i.e., the first coin was a quarter), then when the woman is selecting the second coin, she has in her pocket. In this case, P(Q2) = 1/3. However, if Q1 has not occurred (i.e., the first coin was not a quarter, but a nickel), then when the woman is selecting the second coin, she has in her pocket: In this case, P(Q2) = 2/3.

In these last two examples, we could actually have done some calculation in order to check whether or not the two events are independent or not. Sometimes we can just use common sense to guide us as to whether two events are independent.

The idea of disjoint events is about whether or not it is possible for the events to occur at the same time The idea of independent events is about whether or not the events affect each other in the sense that the occurrence of one event affects the probability of the occurrence of the other

Two people are selected simultaneously and at random from a very large population, and their blood type is checked. A—person 1 has blood type O B—person 2 has blood type O Are the two events disjoint or not disjoint?

disjoint

not disjoint

Explanation :

Since it is possible to choose two people with blood type O, the events are not disjoint.

disjoint

independent

Explanation :

Indeed, since the two people were selected simultaneously and at random from a large population, whether or not event A occurs (whether or not one of the people chosen has blood type O) has absolutely no effect on the probability that the other person chosen will have blood type O (the probability that event B will occur). Therefore, the events are independent.

A seminar class consists of five male students and 5 female students. Two of the 10 students are chosen at random for a role-playing exercise. A—the first chosen is male B—the second chosen is female Are the two events disjoint or not disjoint?

disjoint

not disjoint

Explanation :

Since it is possible to first choose a male and then a female, the two events are not disjoint.

dependent

independent

Explanation :

Indeed, in this case whether or not event A occurs (the first student chosen is male) does have an affect on the probability that event B will occur (the second student chosen is female). If A occurs, then P(second student chosen is female) = 5/9. If A does not occur (i.e., if the first student chosen is female), then P(second student chosen is female) = 4/9. Therefore, the two events are not independent, but rather dependent.

A telemarketer is calling a randomly chosen phone number. A—the person answering the phone is male B—the person answering the phone is female Are the two events disjoint or not disjoint?

disjoint

not disjoint

Explanation :

It is impossible for both events to occur at the same time, since the person can be either male or female, but not both.

A telemarketer is calling a randomly chosen phone number. A—the person answering the phone is male B—the person answering the phone is female Are the two events independent or dependent?

dependent

independent

Explanation :

indeed, In this case, if event A occurs (if the person answering is male), it has a very dramatic effect on the probability that event B will occur (the probability that the person answering is female). If event A occurs, the probability that event B will occur becomes 0. Therefore, the two events are NOT independent but rather dependent.

Suppose that a medical researcher selects one American male at random. Let A represent the event ’the selected male is color blind’. Let B represent the event ’the selected male is not color blind’. Are the two events disjoint or not disjoint?

disjoint

not disjoint

Explanation :

These events are disjoint because they cannot occur at the same time. An individual male cannot be both color blind and not color blind.

independent

dependent

Explanation :

The events are disjoint, so they must be dependent. The occurrence (or not) of event A will affect the probability of B. If A occurs, the P(B) = 0. If A does not occur, then the P(B) = 1

Suppose that a medical researcher selects one American male at random. Let A represent the event 'the first male is color blind'. Let B represent the event 'the second male is not color blind'. Are the two events disjoint or not disjoint?

disjoint

not disjoint

Explanation :

These events can occur simultaneously. If C=color blind and N=not color blind, then the sample space for event A is {CN, CC} and the sample space for event B is {CN, NN}. The sample spaces both contain the outcome CN.

independent

dependent

Explanation :

Since the men are randomly selected from a large population, we can assume that the events are independent. The first man’s color blindness does not affect the probability that the second man is (or is not) color blind.

The Multiplication Rule for Independent Events If A and B are two independent events, then P(A and B) = P(A) * P(B).

Blood Type O A B AB

Probability 0.44 0.42 0.10 0.04

Two people are selected simultaneously and at random from all people in the United States. What is the probability that both have blood type O? Let O1= "person 1 has blood type O" and O2= "person 2 has blood type O" We need to find P(O1 and O2) Since they were chosen simultaneously and at random, the blood type of one has no effect on the blood type of the other. Therefore, O1 and O2 are independent, and we may apply Rule 5: P(O1 and O2) = P(O1) * P(O2) = 0.44 * 0.44 = 0.1936.

A 2011 poll by the Pew Research Center for People and the Press estimated that 62% of U.S. adults favor the death penalty for persons convicted of murder, 31% oppose it, with the remaining 7% undecided. What is the probability that two randomly chosen U.S. adults support the death penalty for persons convicted of murder?

Let A be the event that the first person supports the death penalty. Let B be the event that the second person supports the death penalty. We want to find P(A and B). Since the two people are chosen at random from a large population, A and B are independent and we can use the Multiplication Rule for Independent Events. P(A and B) = P(A) * P(B) = 0.62 * 0.62 = 0.3844

In the 2000 presidential election, George Bush won 48% of the popular vote. In the 2004 presidential election, he won 51% of the popular vote. What is the probability that a randomly chosen voter voted for Bush in both elections?

Let A be the event that the person voted for Bush in 2000. Let B be the event that the person voted for Bush in 2004. The question asks us to determine P(A and B). We might be tempted to use the Multiplication Rule for Independent Events and write P(A and B) = P(A)*P(B) = 0.48*0.51 = 0.2448, but this would be incorrect because these events are not independent. If an individual voted for Bush in 2000, it is likely that the individual voted for him in 2004. So we are unable to answer the question with the information given.

Recall the estimate by the Pew Research Center that 62% of U.S. adults favor the death penalty for murder. The same report gave a much lower estimate for the percentage of U.S. college graduates supporting the death penalty in cases of murder. According to census data from 2000, roughly 28% of U.S. adults have a college degree. What is the probability that a randomly selected U.S. adult has a college degree and favors the death penalty? Let A be the event that a U.S. adult has a college degree. Let B be the event that this person supports the death penalty. We want to find P(A and B).

A and B are dependent events because if A occurs (we have selected a person with a college degree), then the probability of B is affected (a smaller chance that the person supports the death penalty.) So we cannot use the Multiplication Rule for Independent Events in this situation.

Blood Type O A B AB

Probability 0.44 0.42 0.10 0.04

Two people are chosen simultaneously and at random. What is the probability that both have the same blood type? For both to have the same blood type there are four possibilities.

Both have blood type O or both have blood type A or both have blood type B or both have blood type AB. In other words, and using our regular notations,

P(same blood type) = P([O1 and O2] or [A1 and A2] or [B1 and B2] or [AB1 and AB2])

Since our four possibilities of both people having the same blood type are disjoint, using our Addition Rule we can add their probabilities (i.e., replace every "or" with +).

Also, within each of the four possibilities, we can use the Multiplication Rule and replace "and" with * (using the same independence argument as the first example on this page).

Our answer is therefore, About 38% of the time, two randomly chosen U.S. people would have the same blood type.

Note that in this example we used the Addition Rule and the Multiplication Rule one after the other, justifying along the way why it is appropriate to do so.

Modify it to a more specific (or restrictive) event—that not just one randomly chosen person has blood type A, but that out of two simultaneously randomly chosen people, person 1 will have type A and person 2 will have type B—and the probability decreases.

It is important to mention this in order to root out a common misconception. The word "and" is associated in our minds with "adding more stuff."

Therefore, some students incorrectly think that P(A and B) should be larger than either one of the individual probabilities, while it is actually smaller, since it is a more specific (restrictive) event.

Also, the word "or" is associated in our minds with "having to choose between" or "losing something," and therefore some students incorrectly think that P(A or B) should be smaller than either one of the individual probabilities, while it is actually larger, since it is a more general event.

Practically, you can use this comment to check yourself when solving problems. For example, if you solve a problem that involves "or," and the resulting probability is smaller than either one of the individual probabilities, then you know you have made a mistake somewhere.

According to the most updated data gathered by the American Association of Suicidology, 80% of suicides in the U.S. are committed by men. Two suicide cases are selected at random. What is the probability that both suicides were committed by a person of the same gender?

0.68

Cannot be determined since the outcomes are not independent

Cannot be determined since the events are not disjoint

Explanation :

P(both suicides same gender) = P(both males) + P(both females) = (0.8)(0.8) + (0.2)(0.2) = 0.68

Pick a student at random. Let B denote the event that the student ate breakfast this morning; let M denote the event that the student is male. One of the following choices is larger than the other two. Which is it?

P(B)

P(B or M)

P(B and M)

Explanation :

Indeed, the last comment tells us that: "B or M" is a more general event than "B" and therefore has a larger probability. "B and M" is a more specific event than "B" and therefore has a smaller probability.

Pick a student at random. Let B denote the event that the student ate breakfast this morning; let M denote the event that the student is male. One of the following choices is smaller than the other two. Which is it?

P(B)

P(B or M)

P(B and M)

Explanation :

Indeed, the last comment tells us that: "B or M" is a more general event than "B" and therefore has a larger probability. "B and M" is a more specific event than "B" and therefore has a smaller probability.

As we mentioned before, the Addition Rule can be extended to more than two disjoint events. Likewise, the Multiplication Rule can be extended to more than two independent events.

So if A, B and C are three independent events, for example, then P(A and B and C) = P(A) * P(B) * P(C). These extensions are quite straightforward, as long as you remember that "or" requires us to add, while "and" requires us to multiply.

An example of a situation where more than two independent events naturally occur is when a random sample of more than two individuals is chosen from a large population.

A fair coin is tossed 10 times. Which of the following two outcomes is more likely?

HHHHHHHHHH

HTTHHTHTTH

In fact, they are equally likely. The 10 tosses are independent, so we'll use the Multiplication Rule for Independent Events:

P(HHHHHHHHHH) = P(H) * P(H) * ... *P(H) = 1/2 * 1/2 *... * 1/2 = (1/2)¹⁰

P(HTTHHTHTTH) = P(H) * P(T) * ... * P(H) = 1/2 * 1/2 *... * 1/2 = (1/2)¹⁰

My random experiment here is tossing a coin 10 times. You can imagine how huge the sample space is.

There are actually 1,024 possible outcomes to this experiment, all of which are equally likely.

Therefore, while it is true that it is more likely to get an outcome that has 5 heads and 5 tails than an outcome that has only heads (since there is only one possible outcome of the latter kind, and many possible outcomes of the former), if I am comparing 2 specific outcomes as I do here, they are equally likely.

Three people are chosen at random from a large population. What is the probability that all three have blood type B? We'll use the usual notation of B1, B2 and B3 for the events that persons 1, 2 and 3 have blood type B, respectively. We need to find P(B1 and B2 and B3). Let's solve this one together: Are the events B1, B2, and B3 independent or not?

independent

not independent

Explanation :

The probability that one person has blood type B does not affect the probability that either of the other two individuals has blood type B so the events are independent.

In above question What feature of the three people makes the events independent or not?

all have blood type B

are all males

were chosen at random from a large population

Explanation :

When individuals are selected at random from a large population any event associated with one individual is independent of any event associated with the other individual.
SubmitSubmit Your Answer

Should we use the Addition or Multiplication Rule in above case?

Addition Rule

Multiplication Rule

Explanation :

If A and B are two independent events, the Multiplication Rule is used when we try to find the probability for P(A and B).

What is P(B1 and B2 and B3)?

P(B1) * P(B2) * P(B3) = 0.1 * 0.1 * 0.1 = 0.001

P(B1) + P(B2) + P(B3) = 0.1 + 0.1 + 0.1 = 0.3

Explanation :

This is the formula for the Multiplication Rule with three independent events.

A fair coin is tossed 10 times. Which of the following two outcomes is more likely? (a) HHHHHHHHHH (b) HTTHHTHTTH Before we solve this, what does your intuition tell you?

(a) is more likely

(b) is more likely

(a) and (b) are equally likely

Explanation :

The 10 tosses are independent, so we'll use the Multiplication Rule for Independent Events:

P(HHHHHHHHHH) = P(H) * P(H) * ... *P(H) = 1/2 * 1/2 *... * 1/2 = (1/2)¹⁰

P(HTTHHTHTTH) = P(H) * P(T) * ... * P(H) = 1/2 * 1/2 *... * 1/2 = (1/2)¹⁰

Here is the idea:

My random experiment here is tossing a coin 10 times. You can imagine how huge the sample space is.

There are actually 1,024 possible outcomes to this experiment, all of which are equally likely. 
Therefore, while it is true that it is more likely to get an outcome that has 5 heads and 5 tails than 
an outcome that has only heads (since there is only one possible outcome of the latter kind, and many 
possible outcomes of the former), if I am comparing 2 specific outcomes as I do here, they are equally likely.

Three people are chosen at random. (Assume the choices are independent events). What is the probability that they all have the same blood type?

To get all three the same, either the first and the second and the third are type O, or the first and the second and the third are type A, or the first and the second and the third are type B, or the first and the second and the third are type AB. The probability is:

(.44 * .44 * .44) + (.42 * .42 * .42) + (.10 * .10 * .10) + (.04 * .04 * .04) = .160336

About 16% of the time, three randomly chosen people would have the same blood type.

The Complement Rule, P(A) = 1 - P(not A), together with the Multiplication Rule, is extremely useful for finding the probability of events like "at least one of ..." in several repetitions of a random experiment.

For example, 10 people were randomly chosen. Find P(at least one of the 10 has blood type O). A student uses a random guess to answer 10 true/false questions on a test. Find P(the student gets at least one question right). The key here is to use the fact that the complement event is much easier to deal with than the actual event of interest. Going back to our example:

The complement to "at least one of the 10 has blood type O" is "none of the 10 has blood type O."

The complement to "getting at least one question right" is "getting none of the questions right."

(Note how "at least one of" changes to "none" in the complement.)

Example : Two people are selected at random. What is the probability that at least one of them has blood type O?

Here is our sample space S = { (O,O) (O, not O) (not O, O) (not O, not O) }

The event "at least one person chosen has blood type O" consists of the first three possible outcomes, and therefore:

P(at least one person chosen has blood type O) = P((O and O) or (O and not O) or (not O and O)) = (0.44 * 0.44) + (0.44 * 0.56) + (0.56 * 0.44) = 0.6864.

Now we'll just alter the example slightly by randomly choosing 10 people instead of 2:

Example : A patient with blood type O desperately needs a blood transfusion. Since a person with blood type O can receive blood only from another person who has blood type O, the blood bank decides to choose 10 donors at random and hope that at least one of them has blood type O. Find P(at least one of the 10 donors has blood type O). To make things simpler, let's denote the event "at least one has blood type O" by L (for at Least).

Solving this using the brute force method would require a prohibitive amount of work. As before, we would need to list all the possible outcomes of blood types of 10 people (using either "O" or "not O"), but this time there are 1,024 of them!

We would then need to identify those outcomes that L consists of (i.e., the outcomes in which at least one of the 10 people has blood type O).

Next, we would need to find the probability of each of those outcomes and add those probabilities up.

Instead of doing all the work listed above, we can use the Complement Rule, which says P(L) = 1 - P(not L). As we explained before, in this case "not L" is the event "none of the 10 have blood type O," or in other words that all 10 have a blood type other than O. So we can simply solve (using our regular notation from this module):

P(L) = 1 - P(not L) = 1 - P(not O1 and not O2 and not O3 and not O4 and not O5 and not O6 and not O7 and not O8 and not O9 and not O10). Now, using the multiplication rule, = 1 - (0.56 * 0.56 * 0.56 * 0.56 * 0.56 * 0.56 * 0.56 * 0.56 * 0.56 * 0.56) = 1 - 0.003 = 0.997.

Therefore, it is almost certain that if we choose 10 people at random, we'll find that at least one of them has blood type O. This result makes sense, since 44% have blood type O, and so out of 10 people it is almost certain that at least one will have blood type O.

A quiz consists of 10 multiple-choice questions, each with 4 possible answers, only one of which is correct. A student who does not attend lectures on a regular basis has no clue what the answers are, and therefore uses an independent random guess to answer each of the 10 questions. What is the probability that the student gets at least one question right?

Let L be the event that the student gets at least one of the questions right.

We'll use R for getting a question right and W for getting it wrong

There are 4 possible answers and the student chooses one at random, and therefore:

P(R) = 1/4 = 0.25, and P(W) = 3/4 = 0.75

"not L" is the event "the student gets none of the questions right" or in other words, "not L" is the event that the student gets all the questions wrong. And so,

P(not L) = P(getting all the questions wrong) = P(WWWWWWWWWW) = 0.75 * 0.75 * 0.75 * 0.75 * 0.75 * 0.75 * 0.75 * 0.75 * 0.75 * 0.75 = 0.0563.

Using the Complement Rule: P(L) = 1 - P(not L) = 1 - 0.0563 = 0.9437. Thus, it is quite likely that the student will get at least one of the questions right.

According to a study published by the National Institute of Health, during intercourse condom breakage rates fall between 0.4% and 2.3%. Suppose that the breakage rate of Brand X is 2%. A Brand X Pleasure Pack contains 12 condoms. What is the probability that at least one of the condoms in the pack will break during intercourse?

0.02

0.016

0.215

0.785

Explanation :

P(at least one breaks) = 1 - P(none break) = 1 - (0.98)¹² = 0.215

Journey of a Thousand Miles begins with One Click!!!

Probability Rules: Addition Rule for Disjoint Events

Probability Rules: Addition Rule for Disjoint Events

Scenario: Blood Type

Addition Rule for Disjoint Events

Probability Rules: P(A and B) for Independent Events

Disjoint and Independent Events (If events are disjoint then they must be dependent)

Probability Rules: Multiplication Rule for Independent Events

Addition Rule for Disjoint Events and the Multiplication Rule for Independent Events

Probability Rules: Extensions

Probability Rules: At Least One of

Color	Percent
Silver	20.2%
White	18.4%
Black	11.6%
Med/Dark Gray	11.5%
Light Brown	8.8%
Med/Dark Blue	8.5%
Medium Red	6.9%
Med/Dark Green	5.3%
Bright Red	3.8%
Dark Red	0.9%