We checked the independence of the events M (being a male) and E (having pierced ears) by comparing P(E) to P(E | M).

An alternative method of checking for dependence would be to compare P(E | M) with P(E | not M) [same as P(E | F)]. In our case, P(E | M) = 36/180 = 0.2, while P(E | not M) = 288/320 = 0.9, and since the two are very different, we can say that the events E and M are not independent.

In general, another method for checking the independence of events A and B is to compare P(B | A) and P(B | not A). In other words, two events are independent if the probability of one event does not change whether we know that the other event has occurred or we know that the other event has not occurred.

It can be shown that P(B | A) and P(B | not A) would differ whenever P(B) and P(B | A) differ, so this is another perfectly legitimate way to establish dependence or independence

Scenario: Smoke Alarms A homeowner has smoke alarms installed in the dining room (adjacent to the kitchen) and an upstairs bedroom (above the kitchen). The two-way table below shows probabilities of smoke in the kitchen triggering the alarm in the dining room (D) or not, and in the bedroom (B) or not.

A group of 100 college students were surveyed about their gender and whether they had decided on a major.

Offhand, we wouldn't necessarily have any compelling reason to expect that deciding on a major would depend on a student's gender. We can check for independence by comparing the overall probability of being decided to the probability of being decided given that a student is female:

P(D) = 45/100 = 0.45 and P(D | F) = 27/60 = 0.45.

The fact that the two are equal tells us that, as we might expect, deciding on a major is independent of gender. Note from the comment that these must also equal P(D | M), which is 18/40 = 0.45.

Now let's approach the issue of independence in a different way: first, we may note that the overall probability of being decided is 45/100 = 0.45.

And the overall probability of being female is 60/100 = 0.60.

If being decided is independent of gender, then 45% of the 60% of the class who are female should have a decided major; in other words, the probability of being female and decided should equal the probability of being female multiplied by the probability of being decided. If the events F and D are independent, we should have P(F and D) = P(F) * P(D).

In fact, P(F and D) = 27/100 = 0.27 = P(F) * P(D) = 0.45 * 0.60. This confirms our alternate verification of independence.

In general, another method for checking the independence of events A and B is to compare P(A and B) to P(A) * P(B). If the two are equal, then A and B are independent, otherwise the two are not independent.

Let's summarize all the possible methods we've seen for checking the independence of events in one rule:

Two events A and B are independent if any one of the following hold:

P(B | A) = P(B)

P(A and B) = P(A) * P(B)

Comment These various equalities turn out to be equivalent, so that if one equality holds, all are equal, and if one equality does not hold, all are not equal. (This is the case for the same reason that knowing one of the values P(A and B), P(A and not B), P(not A and B), or P(not A and not B), along with P(A) and P(B), allows you to determine the remaining cells of a two-way probability table.)

Therefore, in order to check whether events A and B are independent or not, it is sufficient to check only whether one of the four equalities holds—whichever is easiest for you.

The purpose of the next activity is to practice checking the independence of two events using the four different possible methods that we've provided, and see that all of them will lead us to the same conclusion, regardless of which of the four methods we use.

Recall the delivery services example:

It is vital that a certain document reach its destination within one day. To maximize the chances of on-time delivery, two copies of the document are sent using two services, service A and service B, and the following probability table summarizes the chances of on-time delivery:

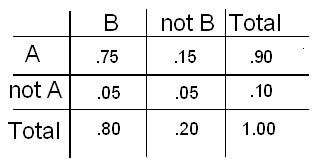
Are the delivery times of the two services independent? In other words, are the events A and B independent? Common sense would say that there will be some degree of dependence between A and B, since the reasons that would cause one service to be delayed (like bad weather, airport delays, etc), would most likely also affect the other service, and cause it to be delayed too. Let's review the four possible methods that we can use to check whether events A and B are independent:

Two events A and B are independent if any one of the following hold:

Use the four different methods to check whether events A and B are independent, and see that indeed all four are leading you to the same conclusion.

Our answer:

Note that all four methods lead us to the same conclusion

We begin with an example that contrasts P(A and B) for independent and dependent cases.

Example : Suppose you pick two cards at random from four cards consisting of one of each suit: club, diamond, heart, and spade, where the first card is replaced before the second card is picked.

What is the probability of picking a club and then a diamond? Because the sampling is done with replacement, whether or not a diamond is picked on the second selection is independent of whether or not a club has been picked on the first selection.

Rule 5, the multiplication rule for independent events, tells us that: - P(C1 and D2) = P(C1) * P(D2) = 1/4 * 1/4 = 1/16.

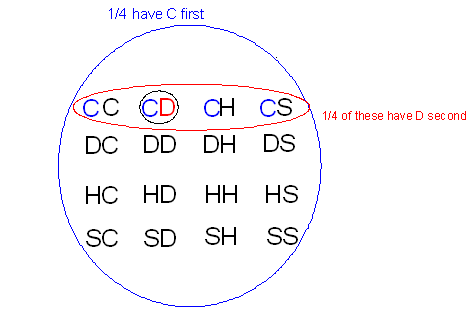
[Here we denote the event "club picked on first selection" as C1 and the event "diamond picked on second selection" as D2.] The display below shows that 1/4 of the time we'll pick a club first, and of these times, 1/4 will result in a diamond on the second pick: 1/4 * 1/4 = 1/16 of the selections will have a club first and then a diamond.

All of the suit possibilities of picking one card, then replacing it and picking a second card. These possibilities are: SC, SD, SH, SS, HC, HD, HH, HS, DC, DD, DH, DS, CC, CD, CH, CS. Note that 1/4 of these have C picked first (the last 4, out of 16 total). Out of these, only one is CD, which is 1/4 of all of the possibilities with C picked first.

Example - Suppose you pick two cards at random from four cards consisting of one of each suit: club, diamond, heart, and spade, without replacing the first card before the second card is picked.

What is the probability of picking a club and then a diamond? The probability in this case is not 1/4 * 1/4 = 1/16; because the sampling is done without replacement, so whether or not a diamond is picked on the second selection does depend on what was picked on the first selection.

(For instance, if a diamond was picked on the first selection, the probability of another diamond is zero!) As in the example above, 1/4 of the time we'll pick a club first. But since the club has been removed, 1/3 of these selections with a club first will have a diamond second.

The probability of a club and then a diamond is 1/4*1/3=1/12; this is the probability of getting a club first, multiplied by the probability of getting a diamond second, given that a club was picked first. Using the notation of conditional probabilities, we can write

P(C1 and D2) = P(C1) * P(D2 | C1) = 1/4 * 1/3 = 1/12.

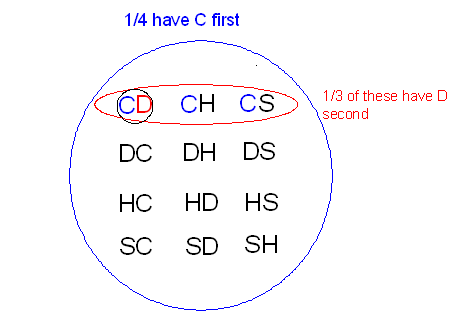
All of the suit possibilities of picking one card then a second card, without replacing any cards. These possibilities are: SC, SD, SH, HC, HD, HS, DC, DH, DS, CD, CH, CS. Note that 1/4 of these have C picked first (the last 3, out of 12 total). Out of these, only one is CD. CD is 1/3 of all of the possibilities with C picked first.

For independent events A and B, we had the rule P(A and B) = P(A) * P(B). Due to independence, to find the probability of both, we could multiply the probability of A by the simple probability of B, because the occurrence of A would have no effect on the probability of B occurring.

Now, for events A and B that may be dependent, to find the probability of both, we multiply the probability of A by the conditional probability of B, taking into account that A has occurred. Thus, our general multiplication rule is stated as follows:

The General Multiplication Rule: For any two events A and B, P(A and B) = P(A) * P(B | A)

For any two events A and B, P(A and B) = P(A) * P(B | A)

Note that although the motivation for this rule was to find P(A and B) when A and B are not independent, this rule is general in the sense that if A and B happen to be independent, then P(B | A) = P(B) is true, and we're back to Rule 5 - the Multiplication Rule for Independent Events: P(A and B) = P(A) * P(B).

The General Multiplication Rule is just the definition of conditional probability in disguise. Recall the definition of conditional probability: P(B | A) = P(A and B) / P(A) Let's isolate P(A and B) by multiplying both sides of the equation by P(A), and we get: P(A and B) = P(A) * P(B | A). That's it ... this is the General Multiplication Rule.

The General Multiplication Rule is useful when two events, A and B, occur in stages, first A and then B (like the selection of the two cards in the previous example). Thinking about it this way makes the General Multiplication Rule very intuitive. For both A and B to occur you first need A to occur (which happens with probability P(A)), and then you need B to occur, knowing that A has already occurred (which happens with probability P(B | A)).

In a certain region, one in every thousand people (0.001) of all individuals are infected by the HIV virus that causes AIDS. Tests for presence of the virus are fairly accurate but not perfect. If someone actually has HIV, the probability of testing positive is 0.95. Let H denote the event of having HIV, and T the event of testing positive.

Express the information that is given in the problem in terms of the events H and T. "one in every thousand people (0.001) of all individuals are infected with HIV" = P(H) = 0.001 "If someone actually has HIV, the probability of testing positive is 0.95" = P(T | H) = 0.95

Use the General Multiplication Rule to find the probability that someone chosen at random from the population has HIV and tests positive. P(H and T) = P(H) * P(T | H) = 0.001*0.95 = 0.00095.

If someone has HIV, what is the probability of testing negative? Here we need to find P(not T | H). Recall from an activity earlier in this module that the Complement Rule works with conditional probabilities as long as we condition on the same event, therefore: P(not T | H) = 1 - P(T | H) = 1 - 0.95 = 0.05.

Scenario: Overheating Engine An overheating engine can quickly cause serious damage to a car, and therefore a dashboard red warning light is supposed to come on if that happens.

In a certain model car, there is a 3% chance that the engine will overheat (event H).

The probability of the warning light showing up (event W) when it should (i.e., when the engine is really overheating) is 0.98. However, 1% of the time the warning light appears for no apparent reason (i.e., when the engine temperature is normal).