Hypothesis Testing for the Population Proportion p: z-test Conditions
Comments
It should now be clear why this test is commonly known as the z-test for the population proportion. The name comes from the fact that it is based on a test statistic that is a z-score.
When we take a random sample of size n from a population with population proportion p, the possible values of the sample proportion \( \hat{p} \) (when certain conditions are met) have approximately a normal distribution with a mean of ... and a standard deviation of ....
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:
The sample has to be random.
The conditions under which the sampling distribution of \( \hat{p} \) is normal are met. In other words:
\( n × p_0 ≥ 10 and n × (1 - p_0) ≥ 10 \)
Here we will pause to say more about condition (i.) above, the need for a random sample.
In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population.
We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them.
For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random.
For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies.
Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall
Example: 1 - The 400 products were chosen at random.
n = 400, , and therefore:
\( * n × p_0 = 80 ≥ 10 * n × (1 - p_0) = 320 ≥ 10 \)
Example: 2 - The 100 students were chosen at random.
n = 100, , and therefore:
\( * n × p_0 = 15.7 ≥ 10 * n × (1 - p_0) = 84.3 ≥ 10 \)
Example: 3 - The 1,000 U.S. adults were chosen at random.
n = 1,000, . 64 , and therefore:
\( * n × p_0 = 640 ≥ 10 * n × (1 - p_0) = 360 ≥ 10 \)
Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. So far we haven't explicitly included it in the 4-step process of hypothesis testing, but now that we are discussing a specific test, you can see how it fits into the process. We are therefore now going to amend our 4-step process of hypothesis testing to include this extremely important part of the process.
The Four Steps in Hypothesis Testing :
State the appropriate null and alternative hypotheses, Ho and Ha.
Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used.
If the conditions are met, summarize the data using a test statistic.
Find the p-value of the test.
Based on the p-value, decide whether or not the results are significant and draw your conclusions in context.
- Explanation :
The population of interest is “registered voters in the county.” Here we are taking a random sample from the population.
- Explanation :
This sample should not be treated as a random sample for this hypothesis test. People shopping at malls might have a more favorable view of their financial situation than the overall population of U.S. adults. Random selection from this group does not control for this bias.
- Explanation :
People who voluntarily respond to Internet surveys typically have a strong opinion (that they are very interested in sharing.) This group will likely have a less favorable view of their financial situation than the population of U.S. adults. Random selection from this group will not control for this bias.
- Explanation :
Telephone surveys like this are commonly used by reputable polling organizations. This is a form of stratified sampling that controls for regional differences in financial circumstances. If the response rate is good, this sample can be viewed as a random sample that represents the population on this issue. Should we be concerned that the survey will not represent the poorest households without phone service? Studies conducted in 2008 by the National Center for Health Statistics concluded that approximately 1.9% of U.S. households have no telephone service. Using phone surveys is the best we can do, short of a full census, to gather information about adults in the United States.
- Explanation :
The study demands may be similar for students enrolled in statistics but different from students enrolled in other types of courses. To test a hypothesis about weekly study hours, we should sample randomly from all students at the college.
- Explanation :
When we consider whether or not a student visits a dentist, there is nothing that distinguishes students taking statistics from other students. So the 200 statistics students could be considered a random sample of all students at the college in this situation.
- Explanation :
When we consider whether or not a student gets financial aid, there is nothing that distinguishes students taking statistics from other students. So the 200 statistics students could be considered a random sample of all students at the college in this situation.
- Explanation :
This sample should not be treated as a random sample in this situation. The courses students take will influence the amount they spend on textbooks. To test a hypothesis about textbook costs, we should sample randomly from all students at the college.
- Explanation :
Indeed n * po = 100 * 0.087 = 8.7 is not large enough since it is less than 10.
- Explanation :
Indeed, all the conditions are met: (a) the sample is random; (b) n * po = 1,308 * 0.75 = 981 ≥ 10; and (c) n * (1 - po) = 1,308 * 0.25 = 327 ≥ 10.
- Explanation :
Even though the sample is random, it is chosen from a specific big metropolitan area and not from the entire population of U.S. households.
- Explanation :
Indeed n * (1 - po) = 40 * (1 - 0.8) = 8 is not large enough since it is less than 10.
Hypothesis Testing for the Population Proportion p: Finding the p-value
Finding the P-value of the Test
Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative) , the further \( \hat{p} \) is from \( p_0 \) , the more evidence we have against Ho.
In the case of the p-value, it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho.
The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret.
On the other hand, the p-value keeps its intuitive appeal across all statistical tests.
How is the p-value calculated?
Intuitively, the p-value is the probability of observing data like those observed assuming that Hois true. Let's be a bit more formal:
Since this is a probability question about the data, it makes sense that the calculation will involve the data summary, the test statistic.
What do we mean by "like" those observed? By "like" we mean "as extreme or even more extreme."
Putting it all together, we get that in general:
The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.
Comment
By "extreme" we mean extreme in the direction of the alternative hypothesis.
Specifically, for the z-test for the population proportion:
If the alternative hypothesis is \(H_a : p < p_0 \) (less than), then "extreme" means small, and the p-value is:
The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
If the alternative hypothesis is \(H_a : p > p_0 \ (greater than), then "extreme" means large, and the p-value is:
The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
if the alternative is \(H_a : p \neq p_0 \ (different from), then "extreme" means extreme in either direction either small or large (i.e., large in magnitude), and the p-value therefore is:
The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.
(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)
Recall the important comment from our discussion about our test statistic, \( z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1 - p_0)}{n}}} \)
which said that when the null hypothesis is true (i.e., when ), the possible values of our test statistic (because it is a z-score) follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.
Less Than
The probability of observing a test statistic as small as that observed or smaller, assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.
\( Ha: p < p_0 ⇒ p-value = P(Z ≤ z) \)
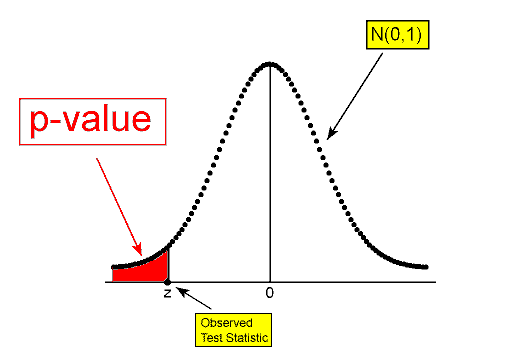
Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.
Greater Than :
The probability of observing a test statistic as large as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution.
\( Ha: p > p_0 ⇒ p-value = P(Z ≥ z) \)
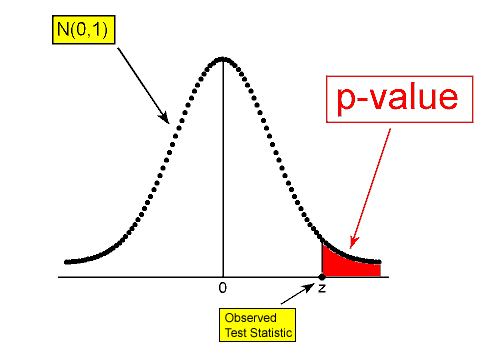
Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.
Not Equal To
The probability of observing a test statistic which is as large as in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.
\( Ha: p ≠ p_0 ⇒ p-value = P(Z < |z|) + P(Z ≥ |z|) = 2P(Z ≥ |z|) \)
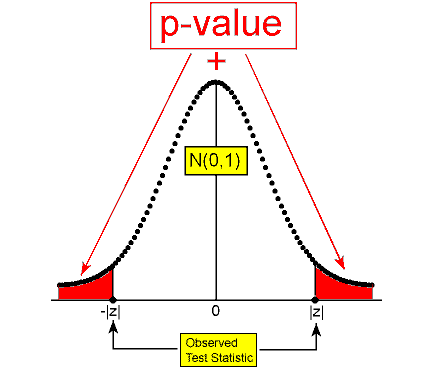
This is often referred to as a two-tailed test, since we shaded in both directions.
- Explanation :
A small p-value (like 0.02) indicates that the sample result is not likely to occur in random sampling from a population in which Ho is true. So a small p-value provides strong evidence against Ho.
- Explanation :
If z = -2, the data's p̂ is 2 standard deviations below po. So it is very unlikely that p̂s from random sampling will be located more standard deviations away from po than the observed data. Hence the small p-value.
- Explanation :
For the alternative hypothesis Ha: p < 0.60, we are asking, "what is the probability of observing a test statistic smaller than that given by the data?" Of the options given, the probability is the smallest for p̂ = 0.40, since it is the furthest from p = 0.60.
- Explanation :
Indeed, for any given po, the p-value of the two-sided test: Ha: p ≠ po is twice as large as the p-value of either one of the one-sided tests.
- Explanation :
In the figure the test statistic is z = -1. Also, the area to the left is shaded in to represent p < 0.56.
- Explanation :
In the figure the test statistic is z = 1 and -1. Also, both tails are shaded in to represent p ≠ 0.56.
- Explanation :
In the figure the test statistic is z = 1. Also, the area to the right is shaded in to represent p > 0.56.
- Explanation :
In the figure the test statistic is z = 1. Also, the area to the left is shaded in to represent p < 0.56
- Explanation :
In the figure the test statistic is z = -1. Also, the area to the right is shaded in to represent p > 0.56.
Hypothesis Testing for the Population Proportion p: The Critical Value Method
We will be emphasizing the use of statistical software in obtaining the exact p-value. The critical value method provides the ability to get an understanding of whether or not a null hypothesis will be rejected at a given probability level (ex. 0.05 or 0.01).
In addition, for the z test, the Normal Table can be used to determine the exact probability level, without the use of statistical software.
Concepts of the Critical Value Method
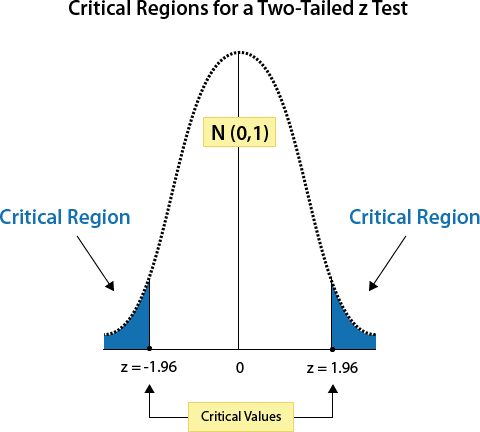
There are several concepts that are important to understand in the critical value method. They are the: 1) critical value and 2) the critical region. As shown in the graph below, the critical value is the value, which cuts off an area referred to as the critical region (or area of rejection), as applied to the z test.
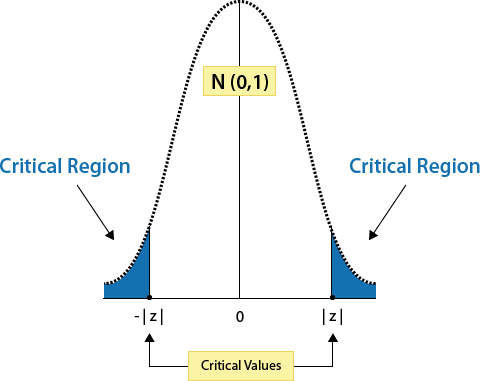
When z test statistics fall in the critical region (the blue shaded areas in the above graph), they are far enough from the mean that they are significantly different from the mean; therefore, in these instances, the null hypothesis would be rejected. The critical region is determined by a critical value that is based on two things: 1) the significance level of the test (either 0.05 or 0.01) AND the direction of the test (ex. left-tailed, right-tailed, or two-tailed).
Not Equal To
For a two-tailed z test, there will be critical regions on both sides of the distribution. For a two-tailed test using a 0.05 level of significance, we need to determine a value that would put 0.025 or 2.5%, in each tail. We can determine this value by using the Normal Table.
First, we need to look in the body of the normal table (click here), where we will see that the exact value 0.0250 is associated with the z score of -1.96; thus, -1.96 is the critical value that puts 0.025 (or 2.5%) in the left tail of the distribution. Since the standard normal distribution is symmetrical, +1.96 is the critical value that puts 0.025 (or 2.5%) in the right tail. Thus, the critical values of -1.96 and +1.96 would define the critical regions for a two-tailed z-test using a 0.05 significance level.
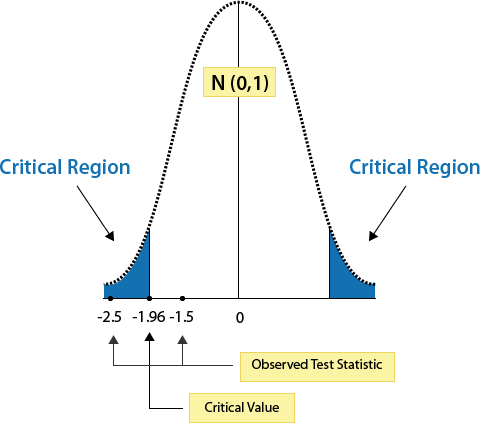
In order to test the null hypothesis, we need to look at where the z-test statistic falls in relation to the critical regions formed by the critical values. In a two-tailed z-test, a z-test statistic of -1.5 would not fall in a critical region Therefore, we know that the p-value would be more than 0.05. Thus, we would not reject the null hypothesis, since the p-value is greater than 0.05 (or, stated another way, p-value > 0.05).
On the other hand, a z-test statistic of -2.5 would fall within the critical region on the left hand side of the distribution; therefore, we know that the p-value would be less than 0.05. In this instance, we would reject the null hypothesis at a less than 0.05 level (or p-value < 0.05). Furthermore, it is possible to figure out the exact p-value for the z-test statistic of -2.5, by using the Normal Table, which is 0.0062.
Less Than
The same logic applies to one-tailed z-tests. For the one-tailed “less than” z-test, the critical value for a 0.05 significance level is -1.645 (note: since the p-value for -1.64 is 0.0505 and the p-value for -1.65 is 0.0495, the critical value for 0.0500 would be between the two z scores or -1.645).
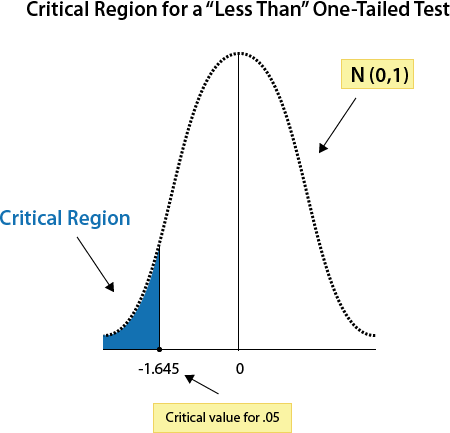
With a “less than” one-tailed z test, any z-test statistic that is less than -1.645, would fall in the critical region and therefore, would have a p-value less than 0.05. For instance, -2.5 would be less than -1.645 and would fall in the critical region. Thus, it would have a p-value less than 0.05 and the null hypothesis would be rejected.
Any z-test statistic that is larger than -1.645 would have a probability level of greater than 0.05 (or p-value > 0.05). For instance, -1.5 would be greater than -1.645 and, therefore, would not fall in the critical region. Thus, it would have a p-value greater than 0.05 and the null hypothesis would not be rejected.
Greater Than
For the one-tailed “greater than” z-test, the critical value for a 0.05 significance level is 1.645.
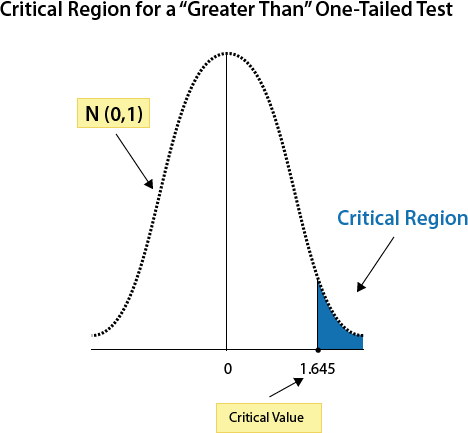
Thus, with a “greater than” one-tailed z test, any z-test statistic larger than 1.645, would fall in the critical region and therefore, would have a p-value less than 0.05. For instance, 2.5 would be greater than 1.645 and would fall in the critical region. Thus, it would have a p-value less than 0.05 (or p-value < 0.05) and the null hypothesis would be rejected .
Any z-test statistic that less than 1.645 would have a probability level of greater than 0.05 (or p-value > 0.05). For instance, 1.5 would be less than 1.645 and, therefore, would not fall in the critical region. Thus, it would have a p-value greater than 0.05 and the null hypothesis would not be rejected.
Wrap-up:
The critical value method uses two concepts: 1) the critical value and 2) the critical region. The critical value is used to determine the critical region and is based on two things: 1) the significance level of the test (either 0.05 or 0.01) AND the direction of the test (ex, left-tailed, right-tailed, or two-tailed).
When z-test statistic falls in the critical region, it is far enough from the mean that it is significantly different from the mean. Therefore, in this instance, the null hypothesis would be rejected at the significance level used to determine the critical region (either 0.05 or 0.01). Furthermore, the actual p-value can be determined by using the Normal Table.
When the z-test statistic does not fall in the critical region, it indicates that it is not far enough from the mean to be significantly different from the mean. In this instance, the null hypothesis would not be rejected.
Comment:
The critical value method has been traditionally used for hypothesis testing (note: there are different critical values and tables for t-tests, ANOVAs, and Chi Square tests). The emphasis now, however, is on the use of exact p-values, which are obtained through the use of statistical software packages.
- Explanation :
The population proportion of 0.47 is being assessed and the assessment is being used to determine whether there were proportionately fewer female matriculated students in rural areas as compared to the national proportion of female matriculated medical students
- Explanation :
The alternative hypothesis would be “less than,” so it would be a one-tailed test, with a negative critical value; thus, -1.645 would put 0.05 (or 5%) in the left side of the distribution.
- Explanation :
The z-test statistic is calculated by using the formula: (value-mean)/(standard deviation) or (.435-.47)/(.1578) = -2.218.
- Explanation :
Since the z-test statistic (-2.218) is less than the critical value for a one-tailed test at the .05 significance level (-1.645), it falls in the critical region. Thus, we can say that the probability of this z-test statistic is less than 0.05. Thus, the null hypothesis is rejected, and we can say that there are proportionately fewer female matriculated female medical students in the rural areas as compared to the national proportion.
- Explanation :
The population proportion of 0.60 is being assessed and the assessment is being used to determine whether there was a change, in either direction, in proportion of Americans, who own pets, between 2006 and 2011.
- Explanation :
The alternative hypothesis would be “not equal to” so it would be a two-tailed test, with both a negative and positive critical value; thus, -1.96 and +1.96 would put 0.025 (or 2.5%) in both the left and right sides of the distribution.
- Explanation :
The z-test statistic is calculated by using the formula: (value-mean)/(standard deviation) or (0.63 - 0.60)/(0.012649) = 2.37
- Explanation :
Since the z-test statistic (2.37) is more than the critical value of +1.96 for a two-tailed test at the 0.05 significance level (1.96), it falls in the critical region. Thus, we can say that the probability of this z-test statistic is less than 0.05. The null hypothesis is rejected, and we can say that there are proportionately more Americans, who own pets in 2011, than 2006
Hypothesis Testing for the Population Proportion p: Interpreting the p-value
Example: 1
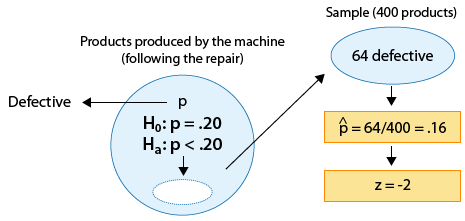
The p-value in this case is:
* The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is 2 standard deviations or more below \(p_0 = 0.2\) , assuming that \( p_0 \) is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion of 9.16 or lower in a random sample of size 400, when the true population proportion is \(p_0 = 0.2\).
In either case, the p-value is found as shown in the following figure:
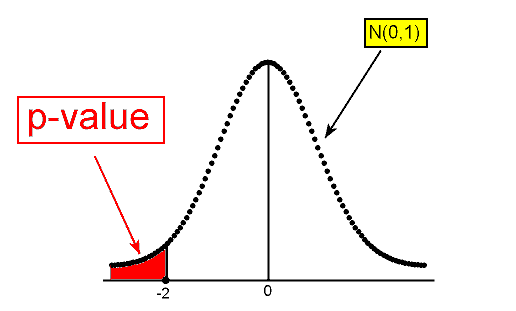
To find P(Z ≤ -2) we can either use a table or software. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells me that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.
Example: 2
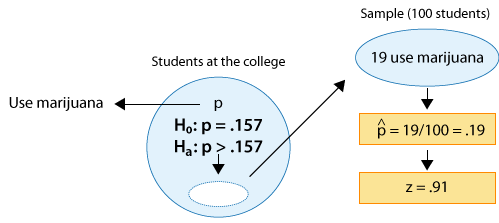
The p-value in this case is:
* The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is 0.91 standard deviations or more above \(p_0 = 0.157\), assuming that \(p_0 \) is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is \(p_0 = 0.157\).
In either case, the p-value is found as shown in the following figure:
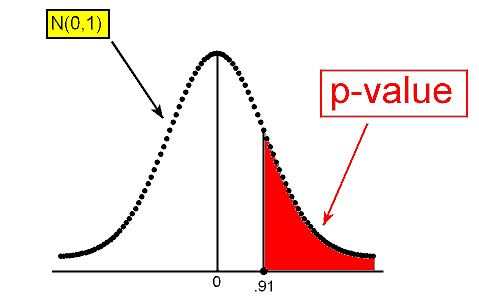
Again, at this point we can either use a table or software to find that the p-value is 0.182.
The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.
Example: 3
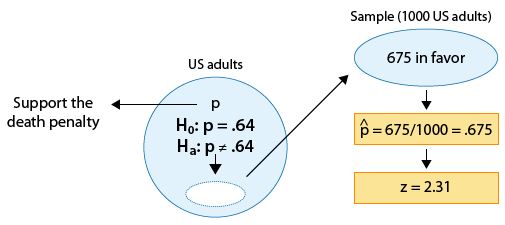
The p-value in this case is:
* The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
OR (recalling what the test statistic actually means in this case),
* The probability of observing a sample proportion that is 2.31 standard deviations or more away from \(p_0 = 0.64\), assuming that \(p_0 \) is the true population proportion.
OR, more specifically,
* The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is \(p_0 = 0.64\).
In either case, the p-value is found as shown in the following figure:
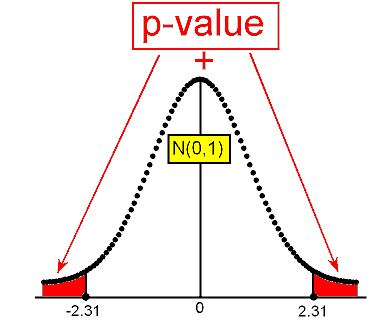
Again, at this point we can either use a table or software to find that the p-value is 0.021.
The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.
Comment
We've just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.
Similarly, in any test, p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the "null distribution" of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1).
We've just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion.
The Four Steps in Hypothesis Testing
State the appropriate null and alternative hypotheses, Ho and Ha.
Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used. If the conditions are met, summarize the data using a test statistic.
Find the p-value of the test.
Based on the p-value, decide whether or not the results are significant, and draw your conclusions in context.
- Explanation :
Every hypothesis test is based on the assumption that Ho is true
- Explanation :
The observed test statistic is the z-value in the output.
- Explanation :
The "<" in Ha tells us to look at sample proportions below the observed p̂ from the data.
- Explanation :
The true population proportion is the po in the null hypothesis.
- Explanation :
Here are several ways you could describe the p-value: This p-value of 0.024 tells us that it is very unlikely to get data like those observed, assuming Ho is true. (This is the least precise description of the four given here.) The p-value is the probability of observing a test statistic as large as 1.98 or larger, assuming Ho is true. The p-value is the probability of observing a sample proportion that is 1.98 standard deviations or more above po = 0.55, assuming that the true population proportion is 0.55. The p-value is the probability of observing a sample proportion of 0.608 or higher in a random sample of size 293 when the true population proportion is 0.55. Check your response to make sure it includes the following elements: (a) The p-value is a probability. (b) The probability is based on the assumption that Ho is true. (c) A statement about the test statistic or sample proportion being higher than (since Ha contains "greater than") what we observed in the data .
- Explanation :
This has the elements of a good interpretation of p-value: 1) The p-value is a probability. 2) The probability is based on the assumption that Ho is true. 3) A statement about results (test statistics or sample proportions) being more extreme than observed in the data. SubmitSubmit Your Answer
- Explanation :
We cannot make a probability statement about whether the drug is not effective. It either is or it isn't. We can only make probability statements about random events, such as the results from random samples.
- Explanation :
We cannot make a probability statement about whether the drug is effective. It either is or it isn't. We can only make probability statements about random events, such as the results from random samples.
Hypothesis Testing for the Population Proportion p: Drawing Conclusions
The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.
We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.
It is important to mention again that this step has essentially two sub-steps:
(i) Based on the p-value, determine whether or not the results are significant (i.e., the data present enough evidence to reject Ho).
(ii) State your conclusions in the context of the problem.
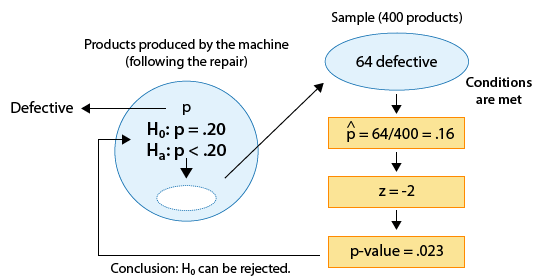
Example: 1
(Has the proportion of defective products been reduced from 0.20 as a result of the repair?)
We found that the p-value for this test was 0.023.
Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho and conclude that as a result of the repair the proportion of defective products has been reduced to below 0.20. The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:
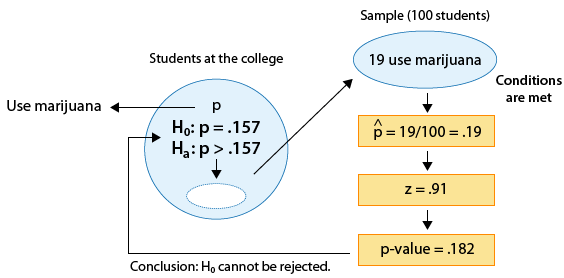
Example: 2
(Is the proportion of students who use marijuana at the college higher than the national proportion, which is 0.157?)
We found that the p-value for this test was 0.182.
Since 0.182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.
We therefore do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure. Here is the complete story of this example:
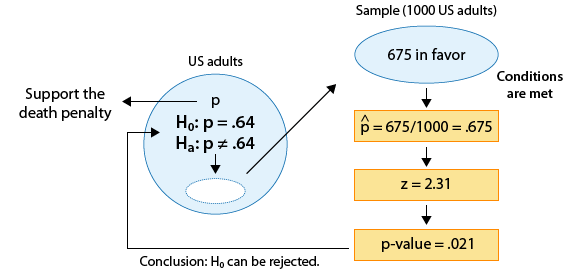
Example: 3
(Has the proportion of U.S. adults who support the death penalty for convicted murderers changed since 2003, when it was 0.64?)
We found that the p-value for this test was 0.021.
Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho, and we conclude that the proportion of adults who support the death penalty for convicted murderers has changed since 2003. Here is the complete story of this example:
Question: Why is 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level.
Answer: This is largely due to just convenience and tradition.
When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%.
Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.
The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value.
There isn’t much meaningful difference, for instance, between a p-value of 0.049 or 0.051, and it would be foolish to declare one case definitely a "real" effect and to declare the other case definitely a "random" effect.
In either case, the study results were roughly 5% likely by chance if there’s no actual effect.
Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.
- Explanation :
Indeed, in test I, the p-value is below the significance level (0.025 less than 0.05) and therefore considered small enough to reject Ho. In test II, on the other hand, where the significance level is set at 0.01, the p-value is not small enough (0.025 greater than 0.01) to reject Ho
- Explanation :
For any level of significance that is below 0.0436, Ho is not rejected and for any level of significance that is above 0.0436, Ho is rejected are both true statements.
Hypothesis Testing for the Population Proportion p: Summary
Step 1
State the null and alternative hypotheses: \(H_0 : p = p_0 \)
\( H_a : p <, >, or ≠ p_0 \)
where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.
Step 2
Obtain data from a sample and:
(i) Check whether the data satisfy the conditions which allow you to use this test.
Random sample (or at least a sample that can be considered random in context) n ⋅ p0 ≥ 10, n ⋅ (1 − p0) ≥ 10
(ii) Calculate the sample proportion \( \hat{p} \), and summarize the data using the test statistic:
\( z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1 - p_0)}{n}}} \).
(Recall: This standardized test statistic represents how many standard deviations above or below \( p_0 \) our sample proportion \( \hat{p} \) is. )
Step 3
Find the p-value of the test either by using software or by using the test statistic as follows:
* for \(H_a : p < p_0: P(Z \leq z)\)
* for \(H_a : p > p_0: P(Z \geq z)\)
* for \(H_a : p \neq p_0: 2P(Z \leq |z|)\)
Step 4
Reach a conclusion first regarding the significance of the results, and then determine what it means in the context of the problem. Recall that:
If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are significant (in the sense that there is a significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho. If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. (Remember, in hypothesis testing we never "accept" Ho).
- Explanation :
The null hypothesis is always a formal statement of "nothing unusual" or "no effect." In this case, the null hypothesis is the formal statement that p (the proportion of contaminated drinking water in the U.S.) is the "proper" baseline rate.
- Explanation :
The question of interest is whether p (the overall proportion of contaminated drinking water in airplanes) is higher than the proportion of contaminated water in the U.S. population.
- Explanation :
z = (0.127 - 0.035) / √((0.035 * (1 - 0.035))/316) = 8.9
- Explanation :
A p-value that is so close to 0 tells us that it would be almost impossible to get a sample proportion of 12.5% (or larger) of contaminated drinking water had the true proportion been 3.5%. In other words, the airline industry cannot claim that this just happened to be a "bad" sample that occurred by chance. A p-value that is essentially 0 tells us that it is highly unlikely that such a sample happened just by chance. Our conclusion is therefore that we have an extremely strong reason to reject Ho and conclude that the proportion of contaminated drinking water on airplanes is higher than the proportion in general. On a technical level, the p-value is smaller than any significance level that we are going to set, so Ho can be rejected.