Diagnosing Bias vs. Variance



  • In this section we examine the relationship between the degree of the polynomial d and the underfitting or overfitting of our hypothesis.


  • We need to distinguish whether bias or variance is the problem contributing to bad predictions.


  • High bias is underfitting and high variance is overfitting. Ideally, we need to find a golden mean between these two.


  • The training error will tend to decrease as we increase the degree d of the polynomial.


  • At the same time, the cross validation error will tend to decrease as we increase d up to a point, and then it will increase as d is increased, forming a convex curve.


  • High bias (underfitting): both \( J_{train}(\Theta) \) and \( J_{CV}(\Theta) \) will be high. Also, \( J_{CV}(\Theta) \approx J_{train}(\Theta) \).


  • High variance (overfitting): \( J_{train}(\Theta) \) will be low and \( J_{CV}(\Theta) \) will be much greater than \( J_{train}(\Theta) \).


  • The is summarized in the figure below:


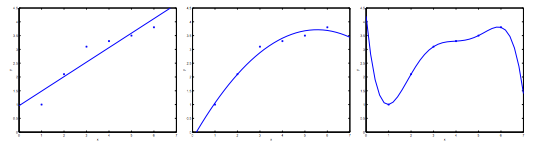
  • bias-variance




Regularization and Bias/Variance



  • bias-variance


  • In the figure above, we see that as \( \lambda \) increases, our fit becomes more rigid.


  • On the other hand, as \( \lambda \) approaches 0, we tend to over overfit the data.


  • So how do we choose our parameter \( \lambda \) to get it 'just right' ? In order to choose the model and the regularization term λ, we need to:


  • Create a list of lambdas (i.e. λ ∈ {0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24});


  • Create a set of models with different degrees or any other variants.


  • Iterate through the \( \lambda \) and for each \( \lambda \) go through all the models to learn some \( \Theta \).


  • Compute the cross validation error using the learned Θ (computed with λ) on the \( J_{CV}(\Theta) \) without regularization or λ = 0.


  • Select the best combo that produces the lowest error on the cross validation set.


  • Using the best combo Θ and λ, apply it on \( J_{test}(\Theta) \) to see if it has a good generalization of the problem.




Learning Curves



  • Training an algorithm on a very few number of data points (such as 1, 2 or 3) will easily have 0 errors because we can always find a quadratic curve that touches exactly those number of points. Hence:


  • As the training set gets larger, the error for a quadratic function increases.


  • The error value will plateau out after a certain m, or training set size. Experiencing high bias:


  • Low training set size: causes \( J_{train}(\Theta) \) to be low and \( J_{CV}(\Theta) \) to be high.


  • Large training set size: causes both \( J_{train}(\Theta) \) and \( J_{CV}(\Theta) \) to be high with \( J_{train}(\Theta) \sim J_{CV}(\Theta) \).


  • If a learning algorithm is suffering from high bias, getting more training data will not (by itself) help much.


  • bias-variance




Experiencing high variance:



  • Low training set size: \( J_{train}(\Theta) \) will be low and \( J_{CV}(\Theta) \) will be high.


  • Large training set size: \( J_{train}(\Theta) \) increases with training set size and \( J_{CV}(\Theta) \) continues to decrease without leveling off. Also, \( J_{train}(\Theta) < J_{CV}(\Theta) \) but the difference between them remains significant.


  • If a learning algorithm is suffering from high variance, getting more training data is likely to help.


  • bias-variance




Deciding What to Do Next



  • Our decision process can be broken down as follows:


    1. Getting more training examples: Fixes high variance


    2. Trying smaller sets of features: Fixes high variance


    3. Adding features: Fixes high bias


    4. Adding polynomial features: Fixes high bias


    5. Decreasing λ: Fixes high bias


    6. Increasing λ: Fixes high variance.


  • Diagnosing Neural Networks


    1. A neural network with fewer parameters is prone to underfitting. It is also computationally cheaper.


    2. A large neural network with more parameters is prone to overfitting. It is also computationally expensive. In this case you can use regularization (increase λ) to address the overfitting.


    3. Using a single hidden layer is a good starting default.


    4. You can train your neural network on a number of hidden layers using your cross validation set. You can then select the one that performs best.




Model Complexity Effects:



  • Lower-order polynomials (low model complexity) have high bias and low variance.


  • In this case, the model fits poorly consistently.


  • Higher-order polynomials (high model complexity) fit the training data extremely well and the test data extremely poorly.


  • These have low bias on the training data, but very high variance.


  • In reality, we would want to choose a model somewhere in between, that can generalize well but also fits the data reasonably well.



UPSCFEVER - POPULAR PAGES