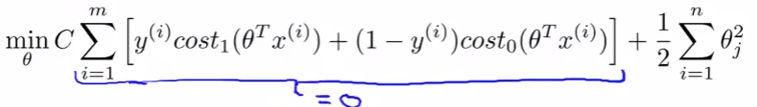Sometimes people refer to SVM as large margin classifiers We'll consider what that means and what an SVM hypothesis looks like The SVM cost function is as above, and we've drawn out the cost terms below

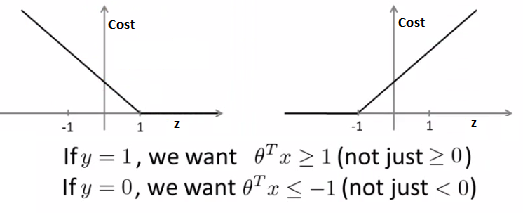
Left is cost1 and right is cost0 What does it take to make terms small

If y =1 cost1(z) = 0 only when z >= 1 If y = 0 cost0(z) = 0 only when z <= -1

Interesting property of SVM If you have a positive example, you only really need z to be greater or equal to 0 If this is the case then you predict 1

SVM wants a bit more than that - doesn't want to *just* get it right, but have the value be quite a bit bigger than zero. It Throws in an extra safety margin factor

Logistic regression does something similar What are the consequences of this? Consider a case where we set C to be huge C = 100,000 So considering we're minimizing CA + B. So for us the A term shown in the figure below must be set to 0.

If C is huge we're going to pick an A value so that A is equal to zero What is the optimization problem here - how do we make A = 0? Making A = 0; If y = 1 ; Then to make our "A" term 0 need to find a value of θ so (\( \theta^T.x \)) is greater than or equal to 1

Similarly, if y = 0 Then we want to make "A" = 0 then we need to find a value of θ so (\( \theta^T.x \)) is equal to or less than -1

So - if we think of our optimization problem a way to ensure that this first "A" term is equal to 0, we re-factor our optimization problem into just minimizing the "B" (regularization) term, because When A = 0 --> A*C = 0 So we're minimizing B, under the constraints shown below

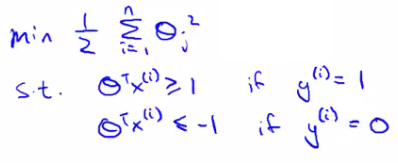
Turns out when you solve this problem you get interesting decision boundaries

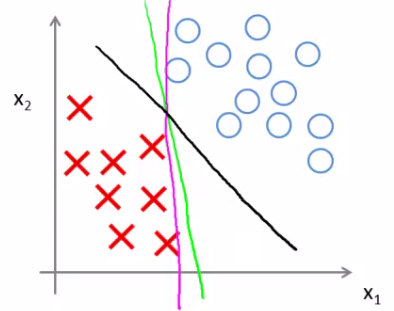
The green and magenta lines are functional decision boundaries which could be chosen by logistic regression. But they probably don't generalize too well

The black line, by contrast is the the chosen by the SVM because of this safety net imposed by the optimization graph. More robust separator Mathematically, that black line has a larger minimum distance (margin) from any of the training examples

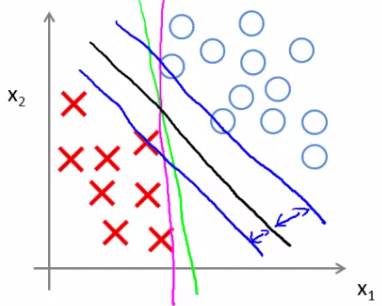
By separating with the largest margin you incorporate robustness into your decision making process. We looked at this at when C is very large. SVM is more sophisticated than the large margin might look

If you were just using large margin then SVM would be very sensitive to outliers

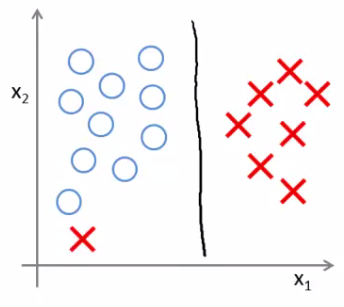
You would risk making a ridiculous hugely impact your classification boundary A single example might not represent a good reason to change an algorithm If C is very large then we do use this quite naive maximize the margin approach

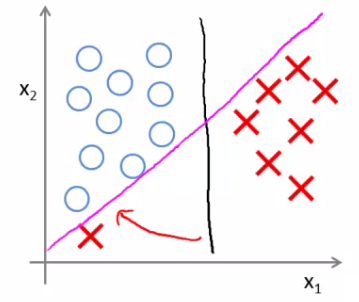
So we'd change the black to the magenta But if C is reasonably small, or a not too large, then you stick with the black decision boundary

What about non-linearly separable data? Then SVM still does the right thing if you use a normal size C So the idea of SVM being a large margin classifier is only really relevant when you have no outliers and you can easily linearly separable data Means we ignore a few outliers