In the clustering problem we are given an unlabeled data set and we would like to have an algorithm automatically group the data into coherent subsets or into coherent clusters for us.

The K Means algorithm is by far the most popular, by far the most widely used clustering algorithm.

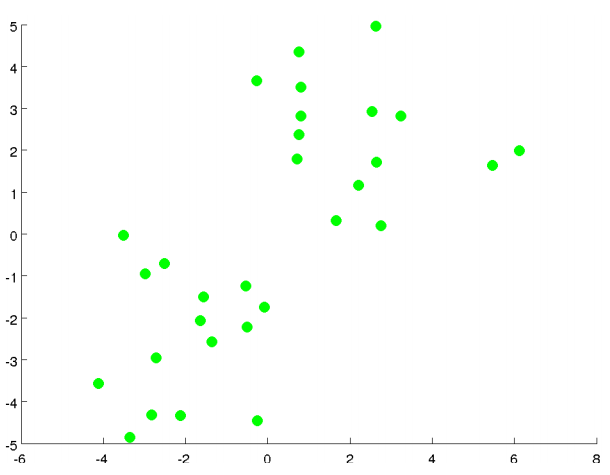
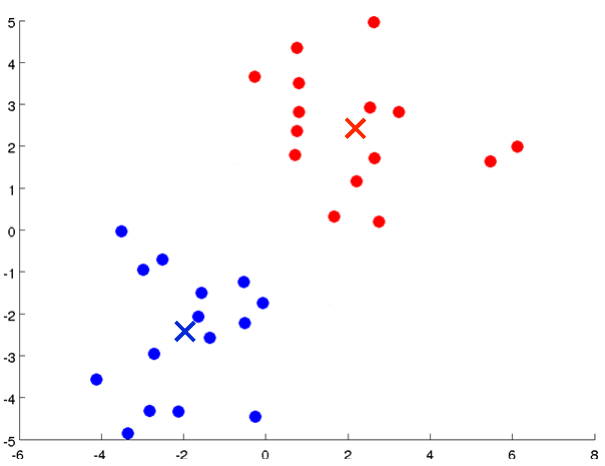
The K means clustering algorithm is best illustrated in pictures. Let's say I want to take an unlabeled data set like the one shown here, and I want to group the data into two clusters.

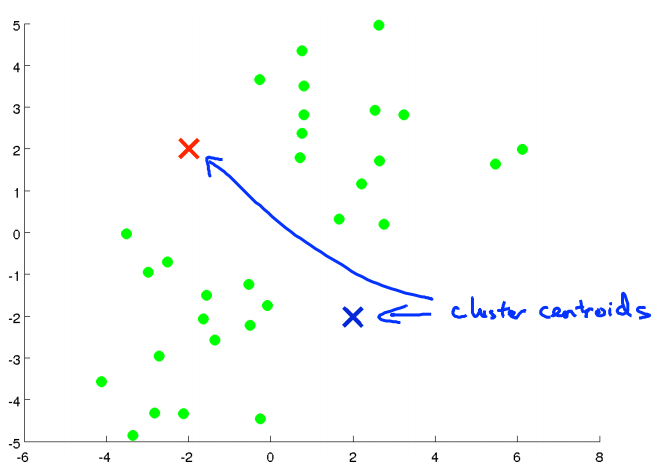
If I run the K Means clustering algorithm, here is what I'm going to do. The first step is to randomly initialize two points, called the cluster centroids. So, these two crosses here, these are called the Cluster Centroids and I have two of them because I want to group my data into two clusters.

K Means is an iterative algorithm and it does two things.

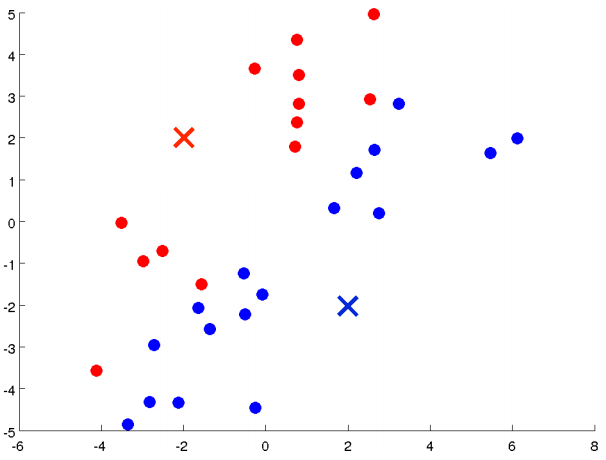
The first of the two steps in the loop of K means, is this cluster assignment step. It's going through each of the examples, each of these green dots shown here and depending on whether it's closer to the red cluster centroid or the blue cluster centroid, it is going to assign each of the data points to one of the two cluster centroids.

Specifically it is to go through your data set and color each of the points either red or blue, depending on whether it is closer to the red cluster centroid or the blue cluster centroid

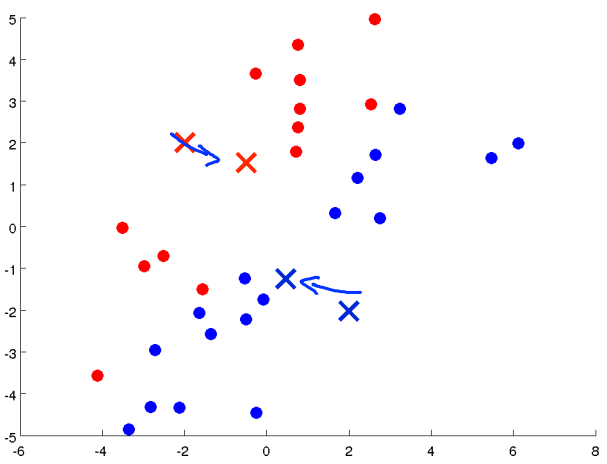
The other part of K means, in the loop of K means, is the move centroid step, and what we are going to do is, we are going to take the two cluster centroids, that is, the red cross and the blue cross, and we are going to move them to the average of the points colored the same colour.

And then we go back to another cluster assignment step, so we're again going to look at all of my unlabeled examples and depending on whether it's closer the red or the blue cluster centroid, I'm going to color them either red or blue. I'm going to assign each point to one of the two cluster centroids, so let me do that now.

. And in fact if you keep running additional iterations of K means from here the cluster centroids will not change any further and the colours of the points will not change any further. And so, this is the, at this point, K means has converged and it's done a pretty good job finding the two clusters in this data.

Let's write out the K means algorithm more formally. The K means algorithm takes two inputs. One is a parameter K, which is the number of clusters you want to find in the data. And then K means also takes as input this sort of unlabeled training set of just the Xs and because this is unsupervised learning, we don't have the labels Y anymore. And for unsupervised learning of the K means I'm going to use the convention that x⁽ⁱ⁾ is an Rⁿ dimensional vector. And that's why my training examples are now N dimensional rather N plus one dimensional vectors.

Input: K (number of clusters in the data) Training set {x1, x2, x3 ..., xn)

Algorithm: Randomly initialize K cluster centroids as {μ1, μ2, μ3 ... μK}

Loop 1 This inner loop repeatedly sets the c(i) variable to be the index of the closes variable of cluster centroid closes to xi i.e. take ith example, measure squared distance to each cluster centroid, assign c(i)to the cluster closest \( \min_k ||x^{(i)} - \mu_k|| \)

Loop 2 Loops over each centroid calculate the average mean based on all the points associated with each centroid from c(i) What if there's a centroid with no data Remove that centroid, so end up with K-1 classes Or, randomly reinitialize it

So far looking at K-means where we have well defined clusters But often K-means is applied to datasets where there aren't well defined clusters e.g. T-shirt sizing

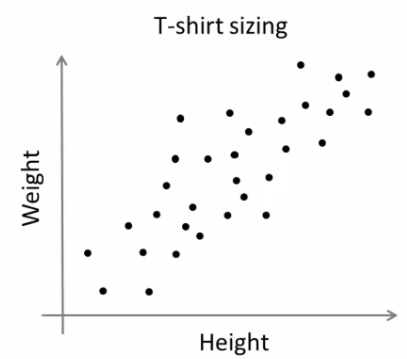
Not obvious discrete groups Say you want to have three sizes (S,M,L) how big do you make these? One way would be to run K-means on this data May do the following

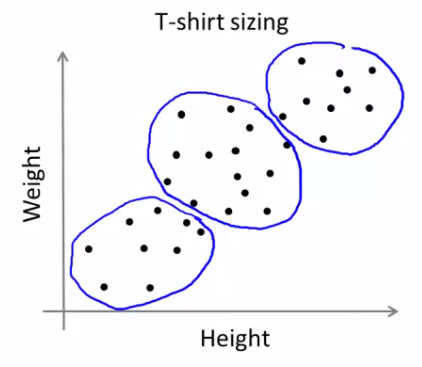
So creates three clusters, even though they aren't really there Look at first population of people Try and design a small T-shirt which fits the 1st population And so on for the other two This is an example of market segmentation Build products which suit the needs of your subpopulations

Supervised learning algorithms have an optimization objective (cost function). K-means does too

K-means has an optimization objective like the supervised learning functions we've seen, Why is this good? Because Knowing this is useful because it helps for debugging and Helps find better clusters

While K-means is running we keep track of two sets of variables cⁱ is the index of clusters {1,2, ..., K} to which xⁱ is currently assigned i.e. there are m number of examples in training data and each example has a cⁱ value, and that value is one the the clusters (i.e. can only be one of K different values)

μk, is the cluster associated with centroid k

μ_cⁱ, is the cluster centroid of the cluster to which example xⁱ has been assigned to. This is more for convenience than anything else. You could look up that example i is indexed to cluster j (using the c vector), where j is between 1 and K. Then look up the value associated with cluster j in the μ vector (i.e. what are the features associated with μ_j)

But instead, for easy description, we have this variable which gets exactly the same value Lets say xⁱ as been assigned to cluster 5 Means that cⁱ = 5 μ_cⁱ = μ5 Using this notation we can write the optimization objective;

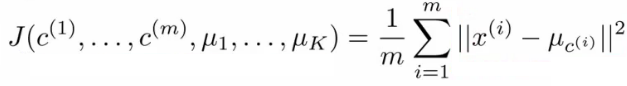
i.e. squared distances between training example xi and the cluster centroid to which xⁱ has been assigned to

This is just what we've been doing, as the visual description below shows;

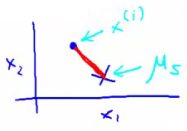
The red line here shows the distances between the example xⁱ and the cluster to which that example has been assigned Means that when the example is very close to the cluster, this value is small

When the cluster is very far away from the example, the value is large This is sometimes called the distortion (or distortion cost function) So we are finding the values which minimizes this function;

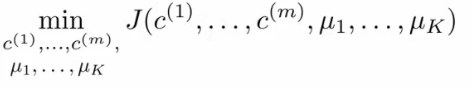
If we consider the k-means algorithm The cluster assigned step is minimizing J(...) with respect to \( c_1, c_2 ... c_i \) i.e. find the centroid closest to each example. This step Doesn't change the centroids themselves

The move centroid step : We can show this step is choosing the values of μ which minimizes J(...) with respect to μ

So, we're partitioning the algorithm into two parts First part minimizes the c variables Second part minimizes the J variables We can use this knowledge to help debug our K-means algorithm

Strategy : How we initialize K-means and how avoid local optimum

Consider clustering algorithm - kmeans. How we initialize the centroids ?

Most recommended : Have number of centroids set to less than number of examples (K < m) (if K > m we have a problem) . Randomly pick K training examples

Set μ₁ up to μ^k to these example's values. K means can converge to different solutions depending on the initialization setup. Risk of local optimum is high.

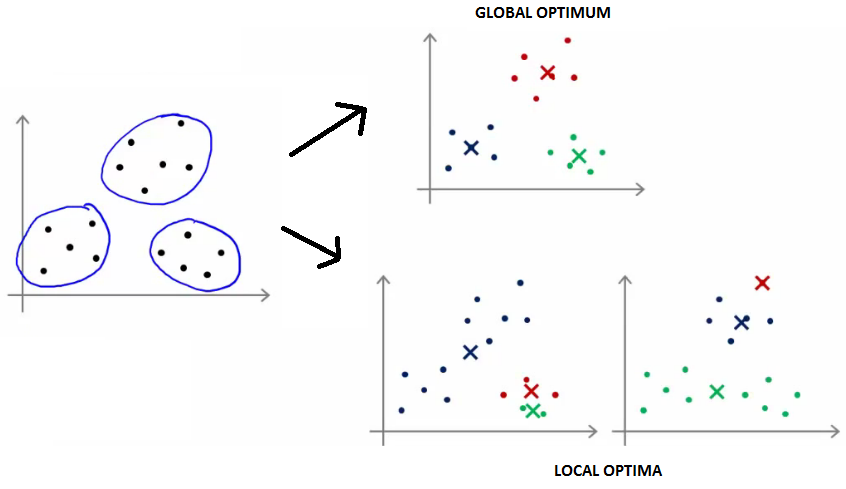
The local optimum are valid convergence, but local optimum not global ones

If this is a concern, We can do multiple random initializations

See if we get the same result - many same results are likely to indicate a global optimum. Algorithmically we can do this as follows;

A typical number of times to initialize K-means is 50-1000. Randomly initialize K-means. For each 100 random initialization run K-means.

Then compute the distortion on the set of cluster assignments and centroids at convergent. End with 100 ways of cluster the data. Pick the clustering which gave the lowest distortion.

If you're running K means with 2-10 clusters can help find better global optimum. If K is larger than 10, then multiple random initializations are less likely to be necessary. First solution is probably good enough (better granularity of clustering)

Choosing K? Not a great way to do this automatically Normally use visualizations to do it manually

What are the intuitions regarding the data? Why is this hard. Sometimes very ambiguous. e.g. two clusters or four clusters

Not necessarily a correct answer. This is why doing it automatic this is hard.

Elbow method : A method to find the right solution. Vary K and compute cost function at a range of K values As K increases J(...) minimum value should decrease (i.e. you decrease the granularity so centroids can better optimize)

Plot this (K vs J()) Look for the "elbow" on the graph

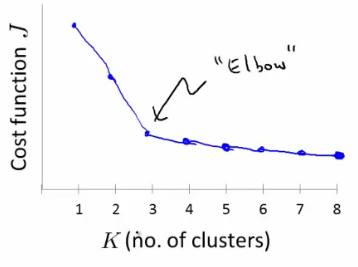
Chose the "elbow" number of clusters If you get a nice plot this is a reasonable way of choosing K Risks Normally you don't get a a nice line -> no clear elbow on curve Not really that helpful

Using K-means for market segmentation Running K-means for a later/downstream purpose. See how well different number of clusters serve you later needs. e.g. T-shirt size example

If you have three sizes (S,M,L) Or five sizes (XS, S, M, L, XL)

Run K means where K = 3 and K = 5 How does this look


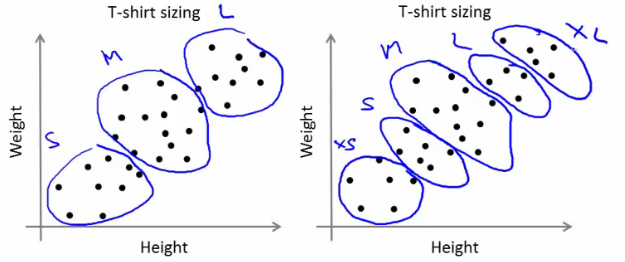
This gives a way to chose the number of clusters

Could consider the cost of making extra sizes vs. how well distributed the products are How important are those sizes though? (e.g. more sizes might make the customers happier)

So applied problem may help guide the number of clusters

Files included in this exercise can be downloaded here ⇒ : Exercise-7