So far we've used the scatterplot to describe the relationship between two quantitative variables, and in the special case of a linear relationship, we have supplemented the scatterplot with the correlation (r).

The correlation, however, doesn't fully characterize the linear relationship between two quantitative variables—it only measures the strength and direction.

We often want to describe more precisely how one variable changes with the other (by "more precisely," we mean more than just the direction), or predict the value of the response variable for a given value of the explanatory variable.

Earlier, we examined the linear relationship between the age of a driver and the maximum distance at which a highway sign was legible, using both a scatterplot and the correlation coefficient.

Suppose a government agency wanted to predict the maximum distance at which the sign would be legible for 60-year-old drivers, and thus make sure that the sign could be used safely and effectively.

Here again is the scatterplot of the drivers' ages and maximum distances at which a sign is legible.

The age for which an agency wishes to predict the legibility distance, 60, is marked in red. How can we make this prediction? It would be useful if we could find a line (such as the one that is presented on the scatterplot) that represents the general pattern of the data.

If we had such a line, we would simply use it to find the distance that corresponds to an age of 60 like this and predict that 60-year-old drivers could see the sign from a distance of just under 400 feet.

The technique that specifies the dependence of the response variable on the explanatory variable is called regression.

When that dependence is linear (which is the case in our examples in this section), the technique is called linear regression. Linear regression is therefore the technique of finding the line that best fits the pattern of the linear relationship (or in other words, the line that best describes how the response variable linearly depends on the explanatory variable).

To understand how such a line is chosen, consider the following very simplified version of the age-distance example

There are many lines that look like they would be good candidates to be the line that best fits the data: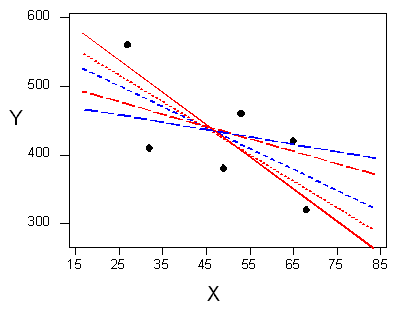

It is doubtful that everyone would select the same line in the plot above. We need to agree on what we mean by "best fits the data"; in other words, we need to agree on a criterion by which we would select this line.

We want the line we choose to be close to the data points. In other words, whatever criterion we choose, it had better somehow take into account the vertical deviations of the data points from the line, which are marked with blue arrows in the plot below

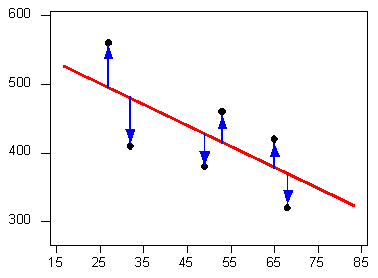
The most commonly used criterion is called the least squares criterion. This criterion says: Among all the lines that look good on your data, choose the one that has the smallest sum of squared vertical deviations.

Visually, each squared deviation is represented by the area of one of the squares in the plot below. Therefore, we are looking for the line that will have the smallest total yellow area.

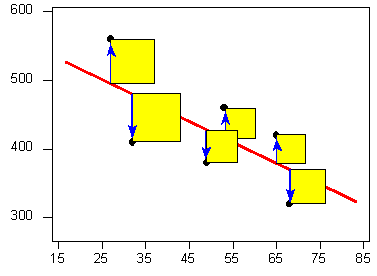
This line is called the least-squares regression line, and, as we'll see, it fits the linear pattern of the data very well.

A line is described by a set of points (X,Y) that obey a particular relationship between X and Y. That relationship is called the equation of the line, which we will express in the following form: Y = a + bX. In this equation, a and b are constants that can be either negative or positive. The reason to write the line in this form is that the constants a and b tell us what the line looks like, as follows:

The intercept (a) is the value that Y takes when X = 0

The slope (b) is the change in Y for every increase of 1 unit in X.

The slope and intercept are indicated with arrows on the following diagram:

Note that if either the intercept (a) or the slope (b) is negative, the corresponding blue arrow on the diagram above would point downward

Example: 1 Consider the line Y = 1 + 1/3 X. The intercept is 1. The slope is 1/3, and the graph of this line is, therefore:

Example: 2 Consider the line Y = 1 - 1/3 X. The intercept is 1. The slope is -1/3, and the graph of this line is, therefore:

While the correlation coefficient is useful for telling us whether two variables are correlated, it does not describe the nature of the relationship between the two variables. Often we know or strongly suspect that two variables are related;

what we want to know is precisely how they are related. For example, it is not surprising that there is a positive relationship between an automobile's speed and its stopping time on dry pavement.

What we want to know is how much stopping distance increases with each speed increase of, say, 10 mph.

Lines are very useful for describing relationships between two variables. Some relationships are much more complicated than lines, but lines always are a useful starting point and are often all we need for many relationships. Before we see how lines are used to model relationships between variables, we will first review the basis of lines and how they work.

The equation for a line is: Y = a + bX

Two variables are related by the two parameters in the equation: a is the intercept and b is the slope. Use the simulation below to explore how these parameters affect the line.

Like any other line, the equation of the least-squares regression line for summarizing the linear relationship between the response variable (Y) and the explanatory variable (X) has the form: Y = a + bX

All we need to do is calculate the intercept a, and the slope b, which is easily done if we know:

\( \overline{X} \)—the mean of the explanatory variable's values

S_X —the standard deviation of the explanatory variable's values

\( \overline{Y} \)—the mean of the response variable's values

S_Y—the standard deviation of the response variable's values

r—the correlation coefficient

Given the five quantities above, the slope and intercept of the least squares regression line are found using the following formulas:

\( b = r * \frac{S_Y}{S_X} ; a = \overline{Y} - b\overline{X} \)

Comments

Note that since the formula for the intercept a depends on the value of the slope, b, you need to find b first.

The slope of the least squares regression line can be interpreted as the average change in the response variable when the explanatory variable increases by 1 unit.

Example: Age-Distance Let's revisit our age-distance example, and find the least-squares regression line. The following output will be helpful in getting the 5 values we need:

Example output from a statistical software package about the data. The mean of the Age is 51, and the mean of the Distance is 423. Standard deviation for Age is 21.78, and for Distance it is 82.8 .

Dependent Variable: Distance

Independent Variable: Age

R (correlation coefficient)= -0.7929

The slope of the line is: b = (-0.7929) * (82.18/21.78) = -3.

This means that for every 1-unit increase of the explanatory variable, there is, on average, a 3-unit decrease in the response variable.

The interpretation in context of the slope being -3 is, therefore: For every year a driver gets older, the maximum distance at which he/she can read a sign decreases, on average, by 3 feet.

The intercept of the line is: a = 423 - (-3 * 51) = 576

and therefore the least squares regression line for this example is:

Distance = 576 + (- 3 * Age)

Here is the regression line plotted on the scatterplot:

The scatterplot for Driver Age and Sign Legibility Distance. The least squares regression line has been drawn. It is a negative relationship line.

As we can see, the regression line fits the linear pattern of the data quite well.

Let's go back now to our motivating example, in which we wanted to predict the maximum distance at which a sign is legible for a 60-year-old. Now that we have found the least squares regression line, this prediction becomes quite easy: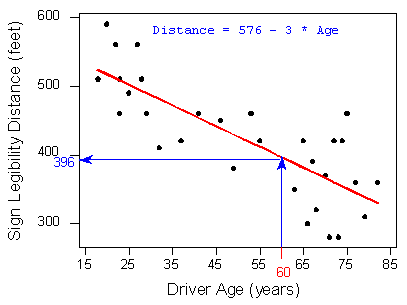

The scatterplot for Driver Age and Sign Legibility Distance. Now that we have a regression line, finding out the maximum distance at which a sign is legible for a 60-year-old person is easy.

We simply check at what y coordinate does the regression line cross a vertical line at x = 60. This happens to be at y = 396.Practically, what the figure tells us is that in order to find the predicted legibility distance for a 60-year-old, we plug Age = 60 into the regression line equation, to find that: Predicted distance = 576 + (- 3 * 60) = 396

396 feet is our best prediction for the maximum distance at which a sign is legible for a 60-year-old.

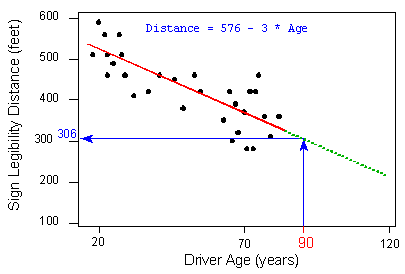
Suppose a government agency wanted to design a sign appropriate for an even wider range of drivers than were present in the original study. They want to predict the maximum distance at which the sign would be legible for a 90-year-old.

Using the least squares regression line again as our summary of the linear dependence of the distances upon the drivers' ages, the agency predicts that 90-year-old drivers can see the sign at no more than 576 + (- 3 * 90) = 306 feet

The scales of both axes have been enlarged so that the regression line has room on the right to be extended past where data exists. The regression line is negative, so it grows from the upper left to the lower right of the plot.

Where the regression line is creating an estimate in between existing data, it is red. Beyond that, where there are no data points, the line is green. This area is x > 82. The equation of the regression line is Distance = 576 - 3 * Age (The green segment of the line is the region of ages beyond 82, the age of the oldest individual in the study.)

Question: Is our prediction for 90-year-old drivers reliable?

Answer: Our original age data ranged from 18 (youngest driver) to 82 (oldest driver), and our regression line is therefore a summary of the linear relationship in that age range only. When we plug the value 90 into the regression line equation, we are assuming that the same linear relationship extends beyond the range of our age data (18-82) into the green segment.

There is no justification for such an assumption. It might be the case that the vision of drivers older than 82 falls off more rapidly than it does for younger drivers. (i.e., the slope changes from -3 to something more negative). Our prediction for age = 90 is therefore not reliable.

In General Prediction for ranges of the explanatory variable that are not in the data is called extrapolation. Since there is no way of knowing whether a relationship holds beyond the range of the explanatory variable in the data, extrapolation is not reliable, and should be avoided. In our example, like most others, extrapolation can lead to very poor or illogical predictions.

When the scatterplot displays a linear relationship, we supplement it with the correlation coefficient (r), which measures the strength and direction of a linear relationship between two quantitative variables.

The correlation ranges between -1 and 1. Values near -1 indicate a strong negative linear relationship, values near 0 indicate a weak linear relationship, and values near 1 indicate a strong positive linear relationship.

The correlation is only an appropriate numerical measure for linear relationships, and is sensitive to outliers. Therefore, the correlation should only be used as a supplement to a scatterplot (after we look at the data).

The most commonly used criterion for finding a line that summarizes the pattern of a linear relationship is "least squares." The least squares regression line has the smallest sum of squared vertical deviations of the data points from the line.

The slope of the least squares regression line can be interpreted as the average change in the response variable when the explanatory variable increases by 1 unit.

The least squares regression line predicts the value of the response variable for a given value of the explanatory variable. Extrapolation is prediction of values of the explanatory variable that fall outside the range of the data. Since there is no way of knowing whether a relationship holds beyond the range of the explanatory variable in the data, extrapolation is not reliable, and should be avoided.