Elementary Graph Algorithms
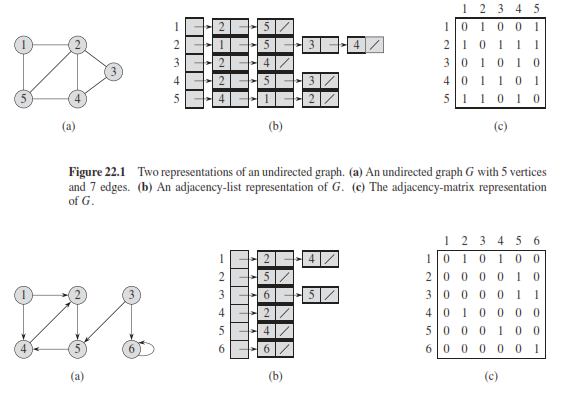
Two standard ways exist to represent a graph G(V,E) : adjacency lists or as an adjacency matrix. Either way applies to both directed and undirected graphs. Because the adjacency-list representation provides a compact way to represent sparse graphs—those for which |E| is much less than \( |V^2| \) - it is usually the method of choice.
We may prefer an adjacency-matrix representation, however, when the graph is dense |E| is close to \( |V^2| \) or when we need to be able to tell quickly if there is an edge connecting two given vertices.
If G is a directed graph, the sum of the lengths of all the adjacency lists is |E| , since an edge of the form (u,v) is represented by having v appear in Adj[u]. If G is an undirected graph, the sum of the lengths of all the adjacency lists is 2|E| , since if (u,v) is an undirected edge, then u appears in v’s adjacency list and vice versa.
For both directed and undirected graphs, the adjacency-list representation has the desirable property that the amount of memory it requires is Θ(V+E).
The adjacency matrix of a graph requires Θ(\( V^2 \)) memory, independent of the number of edges in the graph.
Breadth-first search (Pseudo-code)
BFS (G,s)
for each vertex u ∈ G.V - {s}u.color = white
u.d = ∞
u.π = NIL
s.color = GRAY
s.d = 0
s.π = NIL
Q = φ
ENQUEUE(Q,s)
while Q ≠ φ
u = DEQUEUE(Q)
for each v ∈ G.Adj[u]
if v.color == White
v.color = Gray
v.d = u.d + 1
v.π = u
ENQUEUE(Q,v)
u.color = BLACK
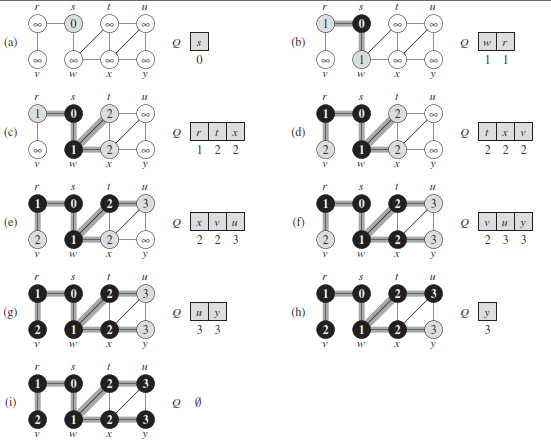
Total running time of the BFS procedure is O(V + E). In a connected graph we enqueue every vertex of the graph, so the worst case runtime becomes \( O(V^2) \)
Depth-first search
DFS(G)
for each vertex u ∈ G.V
u.color = WHITE
u.π = NIL
time = 0
for each vertex u ∈ G.V
if u.color == WHITE
DFS-VISIT(G,u)
DFS-VISIT(G,u)
time = time + 1 // white vertex u has just been discovered
u.d = time
u.color = GRAY
for each v ∈ G.Adj[u] // explore edge (u,v)
if v.color == WHITE
v.π = u
DFS-VISIT(G,v)
u.color = BLACK // blacken u; it is finished
time = time + 1
u.f = time
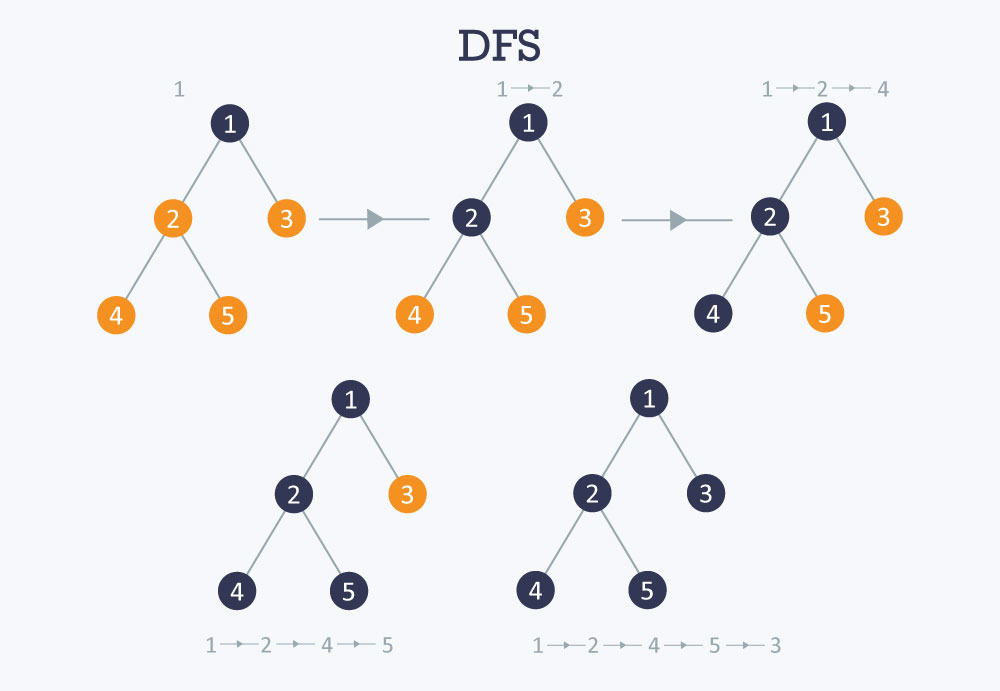
The running time of Depth first search is Θ(V + E).
Rewrite the procedure DFS, using a stack to eliminate recursion.
Algorithm 2: DFS-STACK(G)
for every u ∈ G.V do
u.color = WHITE
u.π = NIL
end for
time = 0
S is an empty stack
while there is a white vertex u in G do
S.push(u)
while S is nonempty do
v = S:pop
time++
v.d = time
for all neighbors w of v do
if w.color == WHITE then
w.color = GRAY
w.π = v
S.push(w)
end if
end for
time++
v.f = time
end while
end while
Minimum Spanning Tree
For a connected, undirected and weighted graph G(V,E) where edges are (u,v) ∈ E and w(u,v) is weight of edge (u,v). A minimum spanning tree is an acyclic subset T ⊆ E that connects all of the vertices and whose total weight is given by
\( w(T) = \sum_{(u,v) \in T} w(u,v) \) is minimized.
We have two greedy algorithms: Prims and Kruskal's which run in O(E lgV) time.
Other features of spanning trees are that: No self loops are present, no cycles or parallel edges are seen. In Kruskals, algorithm during the intermediate steps the tree is lost but not in Prims. Maximum number of minimum spanning trees possible are nn-2 in a connected, undirected graph of 'n' nodes.
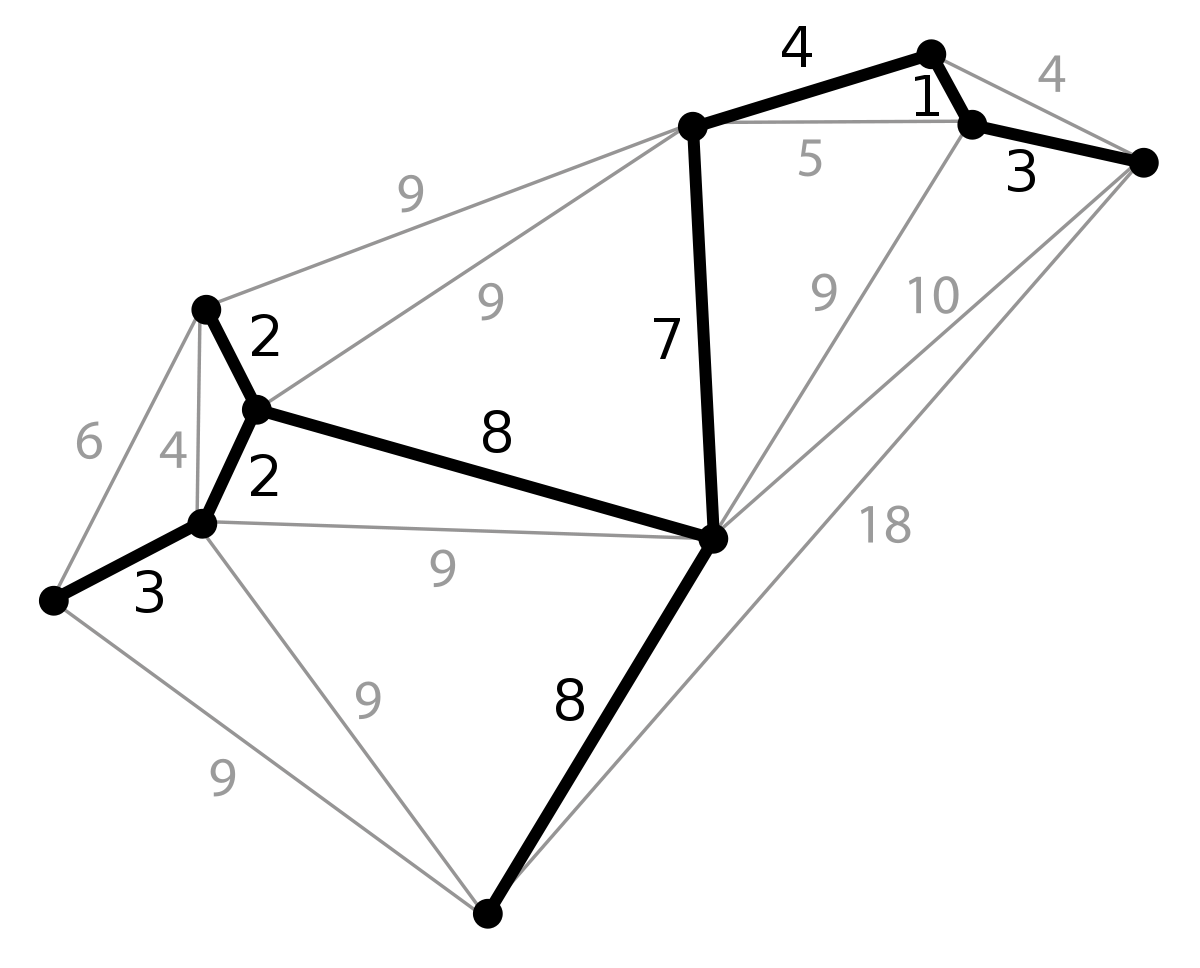
Minimum Spanning Tree - Kruskal's Algorithm
FUNCTION MST_KRUSKAL(G,w)
A = φ
for each vertex v ∈ G
make-set(v)
sort the edge of G into non decreasing order of weight
for each edge (u,v) ∈ G
Take E from the sorted list
if findset(u) ≠ findset(v)
A = A ∪ {(u,v)}union(u,v)
return A;
Kruskal's Algorithm - Working
Step 1: Initially consider each set is a different vertex so we have {
Consider edge {1,2} so u = 1 and v = 2 then findset(1) = {1} ≠ findset(2) = {2} and so we include edge {1,2} and take union of u,v to get {1,2}.
Now Consider edge {3,6} so u = 3 and v = 6 then findset(3) = {3} ≠ findset(6) = {6} and so we include edge {3,6} and take union of u,v to get {3,6}.
Now Consider edge {4,6} so u = 4 and v = 6 then findset(4) = {4} ≠ findset(6) = {3,6} and so we include edge {4,6} and take union of u,v to get A = {3,4,6}.
Now Consider edge {2,6} so u = 2 and v = 6 then findset(2) = {1,2} ≠ findset(6) = {3,4,6} and so we include edge {2,6} and take union of u,v to get {1,2,3,4,6}.
Now Consider edge {1,4} so u = 1 and v = 4 then findset(1) = {1,2,3,4,6} ≠ findset(4) = {1,2,3,4,6} and so we reject edge {1,4}.
Now Consider edge {3,5} so u = 3 and v = 5 then findset(3) = {1,2,3,4,6} ≠ findset(5) = {5} and so we include edge {3,5} and take union of u,v to get {1,2,3,4,5,6}.
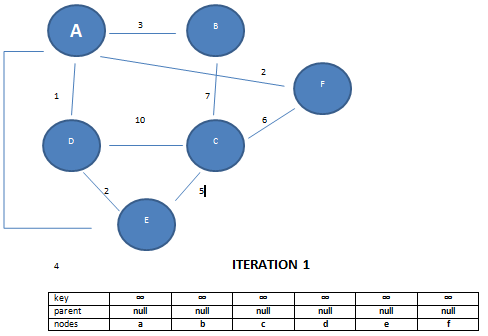
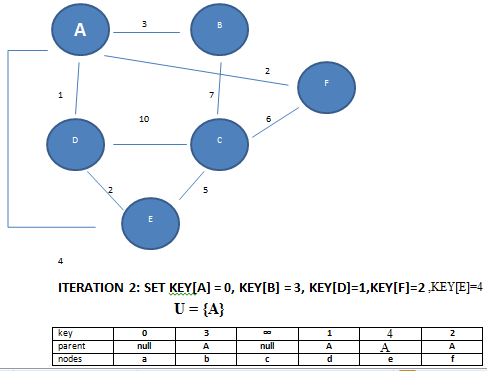
Minimum Spanning Tree - Prim's Algorithm
PRIMS(G,w)
A = null
for each v ∈ V
key[v] = ∞
parent[v] = null
key[r] = 0
Q = V
while Q! = null
u = min(Q) by key value
Q = Q - u
if parent[u]! = null
A = A ∪ (u, parent(u))
for each v ∈ Adj[u]
if v ∈ Q and w(u,v) < key[v] then
parent[v] = u
key[v] = w
return A
Prim's Algorithm - Working





Kruskal's Algorithm v.s Prim's Algorithm
| Kruskals algorithm | Prims algorithm |
|---|---|
| Better for sparse graphs | Better for dense graphs |
| Graphs can be unconnected too | Graph has to connected |
| Next edge is selected based on previous edge or vertex | next edge is selected based on minimal value of adjacency edges of previous vertex |
| Every edge is considered only once | Not the case |
Solved Question Papers
Q.3 Let G = (V, E) be a simple undirected graph, and s be a particular vertex in it called the source. For x V, let d(x) denote the shortest distance in G from s to x. A breadth first search (BFS) is performed starting at s. Let T be the resultant BFS tree. If (u, v) is an edge of G that is not in T, then which one of the following CANNOT be the value of d(u) – d(v)?.(Gate 2015 Set1)
-1
0
1
2
Ans (D)
The given graph is undirected, so an edge (u, v) also means (v, u) is also an edge. Since a shorter path can always be obtained by using edge (u, v) or (v, u), the difference between d(u) and d(v) can not be more than 1.
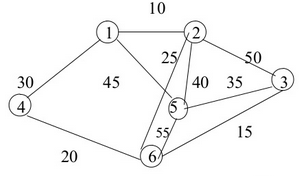
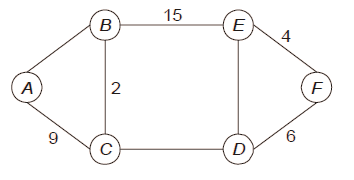
Q.9 The graph shown below 8 edges with distinct integer edge weights. The minimum spanning tree (MST) is of weight 36 and contains the edges: {(A, C), (B, C), (B, E), (E, F), (D, F)}. The edge weights of only those edges which are in the MST are given in the figure shown below. The minimum possible sum of weights of all 8 edges of this graph is ______________.(Gate 2015 Set1)
66
69
38
70
Ans (B)
In every cycle, the weight of an edge that is not part of MST must by greater than or equal to weights of other edges which are part of MST. Since all edge weights are distinct, the weight must be greater. So the minimum possible weight of ED is 7, minimum possible weight of CD is 16 and minimum possible weight of AB is 10. Therefore minimum possible sum of weights is 69.
Q.3.Consider a complete undirected graph with vertex set {0, 1, 2, 3, 4}. Entry \( W_{ij} \) in the matrix W below is the weight of the edge {i, j}. What is the minimum possible weight of a spanning tree T in this graph such that vertex 0 is a leaf node in the tree T?(GATE 2010)
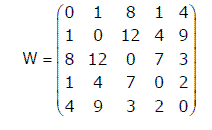
7
8
9
10
Ans . 4
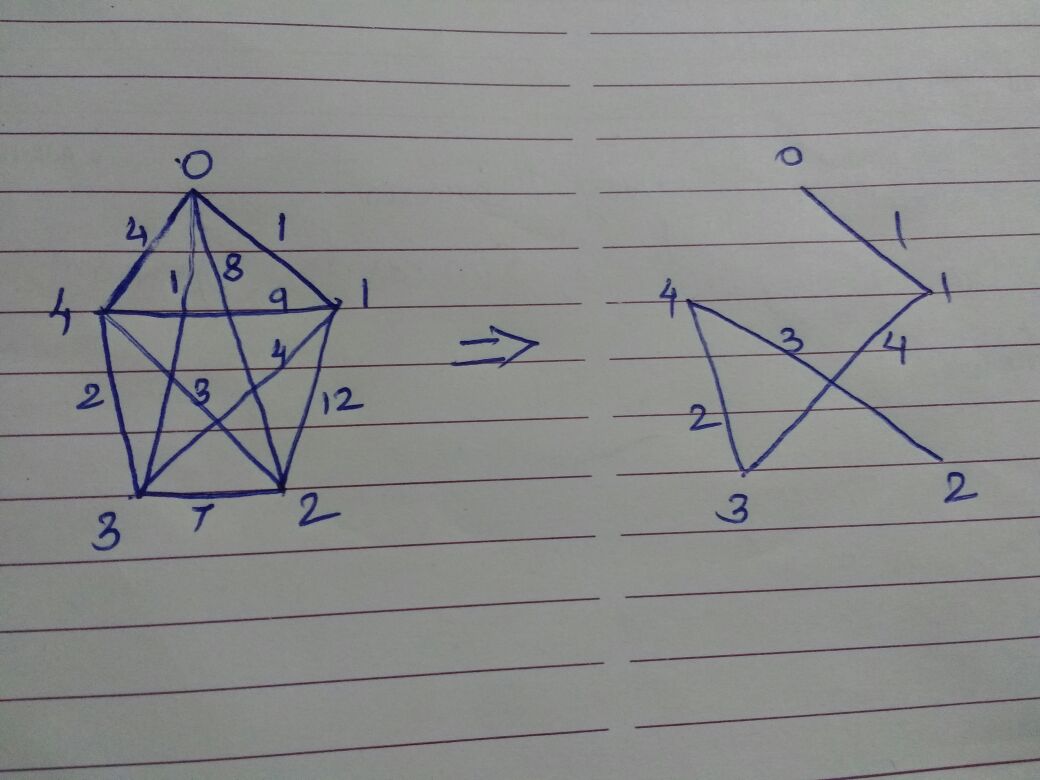
V0 V1 V2 V3 V4
For minimum cost we go from V0 to V1 = 1, V1 to V4 = 4, V4 to V3 = 2, V3 to V2 = 3
1+4+2+3=10
Hence 4.
Q.4.In the graph given in above question, what is the minimum possible weight of a path P from vertex 1 to vertex 2 in this graph such that P contains at most 3 edges?(GATE 2010)
7
8
9
10
Ans . 2
Path: 1 -> 0 -> 4 -> 2
Weight: 1 + 4 + 3
Hence 2.
Q. 1 Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is _____. (GATE 2016 SET B)
Ans . 31
Solution steps: 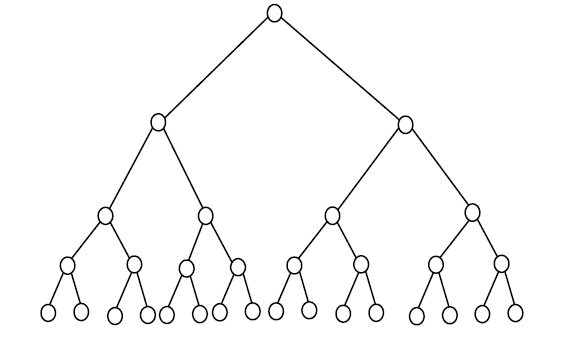
Required vertex is 31st vertex.
Q.An undirected graph G(V,E) contains n (n>2) nodes named v1 , v2,....,vn. Two
nodes vi , vj are connected if and only if 0<|i-j|<=2. Each edge (vi,vj) is
assigned a weight i+j. A sample graph with n=4 is shown below
What will be the cost of the minimum spanning tree (MST) of such a graph with n
nodes?
(GATE 2011)
(11n2-5n)/12
n2-n+1
6n-11
2n+1
Ans . 2
n2-n+1
Q.An undirected graph G(V,E) contains n (n>2) nodes named v1 , v2,....,vn. Two
nodes vi , vj are connected if and only if 0<|i-j|<=2. Each edge (vi,vj) is
assigned a weight i+j. A sample graph with n=4 is shown below
The length of the path from v5 to v6 in the MST of previous question with n=10
is
(GATE 2011)
11
25
31
41
Ans . 3
Q.6Consider the weighted undirected graph with 4 vertices, where the
weight of edge i, j is given by the entry Wij in the matrix W.
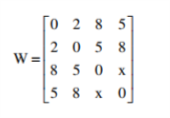
The largest possible integer value of x, for which at least one shortest path
between some pair of vertices will contain the edge with weight x is _____(GATE 2016 SET A)
Ans : 12
Solution steps:
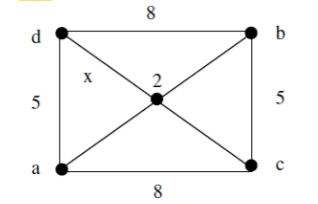
If x=12 then the shortest path between 'd' and 'c' will contain edge with lable x.
Q.7 Let G be a complete undirected graph on 4 vertices, having 6 edges with weights being 1, 2, 3, 4, 5, and 6.The maximum possible weight that a minimum weight spanning tree of G can have is_____ (GATE 2016 SET A)
Ans : 7
Solution steps:
Q.8 G = (V, E ) is an undirected simple graph in which each edge has a
distinct weight, and e is a particular edge of G. Which of the following statements
about the minimum spanning trees (MSTs) of G is/are TRUE?
I. If e is the lightest edge of some cycle in G, then every MST of G includes e
II.If e is the heaviest edge of some cycle in G, then every MST of G excludes e (GATE 2016 SET A)
I only
II only
Both I and II
Neither I nor II
Ans : (B) II only
Solution steps:
the MSTs of G may or may not include the lightest edge.Let the heavies edge be e. Suppose the minimum spanning tree which contains e. If we add one more edge to the spanning tree we will create a cycle. Suppose we add edge e’ to the spanning tree which generated cycle C. We can reduce the cost of the minimum spanning tree if we choose an edge other than e from C for removal which implies that e must not be in minimum spanning tree and we get a contradiction.
Q.4 Let G be a weighted connected undirected graph with distinct positive
edge weights. If every edge weight is increased by the same value, then which
of the following statements is/are TRUE?
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices does not change (GATE 2016 SET A)
P only
Q only
Neither P nor Q
Both P and Q
Ans : (A)
Solution steps:
The shortest path may change. The reason is, there may be different number of edges in different paths from s to t. For example, let shortest path be of weight 15 and has 5 edges. Let there be another path with 2 edges and total weight 25. The weight of the shortest path is increased by 5*10 and becomes 15 + 50. Weight of the other path is increased by 2*10 and becomes 25 + 20. So the shortest path changes to the other path with weight as 45.The Minimum Spanning Tree doesn’t change. Remember the Kruskal’s algorithm where we sort the edges first. IF we increase all weights, then order of edges won’t change.
Q.2Consider the following directed graph:
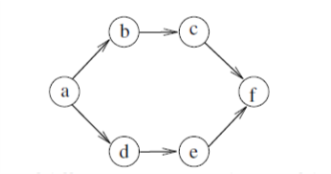
The number of different topological orderings of the vertices of the graph is _____(GATE 2016 SET A)
Ans : 6
Solution steps:
a b c d e f
a d e b c f
a b d c e f
a d b c e f
a b d e c f
a d b e c f
Q. The Breadth First Search (BFS) algorithm has been implemented using the queue data structure. Which one of the following is a possible order of visiting the nodes in the graph below? (GATE 2017 Paper 2)
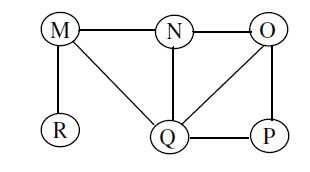
-
MNOPQR
-
NQMPOR
-
QMNROP
-
POQNMR
Ans. 4
BFS: Start at root (some arbitrary node of a graph, sometimes referred to as "search key") and explore the neighbor nodes first, before and moving to the next level of neighbors. Use queue for BFS.
| Option No. | Option | Visited Vertices | Remaining Vertices in the Queue |
|---|---|---|---|
| 1 | MNOPQR | M | N R |
| M N | R O Q | ||
| M N R | O Q | ||
| 2 | NQMPOR | N | Q M O |
| N Q | M O P | ||
| N Q M | O P R | ||
| 3 | QMNROP | Q | M N O P |
| Q M | N O P R | ||
| 4 | POQNMR | P | O Q |
| P O | Q N | ||
| P O Q | N M | ||
| P O Q N | M | ||
| P O Q N M | R | ||
| P O Q N M R |
Q. Match the algorithms with their time complexities: (GATE 2017 Paper 2)
| Algorithm | Time Complexity | ||
|---|---|---|---|
| P. | Towers of Hanoi with n disks | i. | \[\ominus\left(n^{2}\right)\] |
| Q. | Binary search given n sorted numbers | ii. | \[\ominus\left(n\log{n}\right)\] |
| R. | Heap sort given n numbers at the worst case | iii. | \[\ominus\left(2^{n}\right)\] |
| S. | Addition of two n × n matrices | iv. | \[\ominus\left(\log{n}\right)\] |
-
P-(iii),Q-(iv), R-(i), S-(ii)
-
P-(iv),Q-(iii), R-(i), S-(ii)
-
P-(iii),Q-(iv), R-(ii), S-(i)
-
P-(iv),Q-(iii), R-(ii), S-(i)
Ans. 3
P. Towers of Hanoi \(\Rightarrow T\left(n\right) = 2T\left(n-1\right) + 1 \Rightarrow \ominus\left(2^{n}\right)\)
Q. Binary search \(\Rightarrow T\left(n\right) = T\left(n/2\right) + C \Rightarrow \ominus\left(\log{n}\right)\)
R. Heap sort \(\Rightarrow \ominus\left(n\log{n}\right)\)
S. Addition of two n × n matrices \(\Rightarrow \ominus\left(n^{r}\right)\)
Q. Consider a binary code that consists of only four valid code words as given below: 00000,01011,10101,11110. Let the minimum Hamming distance of the code be p and the maximum number of erroneous bits that can be corrected by the code be q. Then the values of p and q are (GATE 2017 Paper 2)
-
p = 3 and q = 1
-
p = 3 and q = 2
-
p = 4 and q = 1
-
p = 4 and q = 2
Ans. 1
Given :
code1: 00000
code2: 01011
code3: 10101
code4: 11110
Hamming distance between code 1 and code 2 is 3.
Hamming distance between code 1 and code 3 is 3.
Hamming distance between code 1 and code 4 is 4.
Hamming distance between code 2 and code 3 is 4.
Hamming distance between code 2 and code 4 is 3.
Hamming distance between code 3 and code 4 is 3.
So, as per Hamming code, minimum Hamming distance of all code words is considered as Hamming distance i.e., 3 (p).
Now, the max number of erroneous bits that can be corrected by the Hamming code is 2d + 1.
So, 2d +1 = 3 ⇒ d =1
So, option 1 is correct.
Q. Consider the recurrence function (GATE 2017 Paper 2)
\(T\left(n\right) = \begin{cases}2T\left(\sqrt{n}\right) + 1 & n >2\\2 & 0 \leq n \leq 2\end{cases}\)Then T(n) in terms of Θ notation is
-
\(\ominus\left(\log{\log{n}}\right)\)
-
\(\ominus\left(\log{n}\right)\)
-
\(\ominus\left(\sqrt{n}\right)\)
-
\(\ominus\left(n\right)\)
Ans. 1
\(T\left(n\right) = 2T\left(\sqrt{n} \right) + 1\)
\(n = 2^{k}\)
\(T\left(2^{k}\right) = 2T\left(2^{k/2} \right) + 1\)
Assume \(T\left(2^{k}\right) = \partial\left(k\right)\)
\(\Rightarrow \partial\left(k\right) = 2\partial\left(k/2\right) + 1\)
By Master's theorem,
\(\Rightarrow \partial\left(k\right) = \ominus\left(k\right)\)
\(T\left(2^{n}\right) = \ominus\left(k\right)\)
\(T\left(n\right) = \ominus\left(\log{n}\right)\)
\(2^{k} = n\)
Q. Consider the following graph (GATE 2009)
Which of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm?
(A) (b,e) (e,f) (a,c) (b,c) (f,g) (c,d)
(B) (b,e) (e,f) (a,c) (f,g) (b,c) (c,d)
(C) (b,e) (a,c) (e,f) (b,c) (f,g) (c,d)
(D) (b,e) (e,f) (b,c) (a,c) (f,g) (c,d)
Ans . D
In the sequence (b, e) (e, f) (b, c) (a, c) (f, g) (c, d) given option D, the edge (a, c) of weight 4 comes after (b, c) of weight 3. In Kruskal’s Minimum Spanning Tree Algorithm, we first sort all edges, then consider edges in sorted order, so a higher weight edge cannot come before a lower weight edge.
Q.5 An undirected graph G(V, E) contains n ( n > 2 ) nodes named v1 , v2 ,….vn. Two nodes vi , vj are connected if and only if 0 < |i – j| <= 2. Each edge (vi, vj ) is assigned a weight i + j. A sample graph with n = 4 is shown below. What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?(GATE 2011)
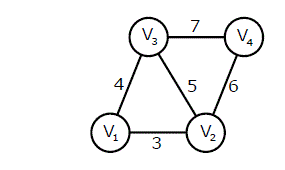
1/12(11n^2 – 5n)
n^2 – n + 1
6n – 11
- 2n + 1
Ans . (B)
Minimum spanning tree for 2 nodes would be (V1)_(V2) : Total weight :3
Minimum spanning tree for 3 nodes would be
: Total weight :3+4=7
Minimum spanning tree for 4 nodes would be
: Total weight :3+4+6=13
Minimum spanning tree for 5 nodes would be
: Total weight :3+4+6+8=21
Minimum spanning tree for 6 nodes would be
: Total weight :3+4+6+8+10=31
Q. The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is (GATE Paper-2008)
MNOPQR
NQMPOR
QMNPRO
QMNPOR
Ans . (3)
Explaination :
The Breadth First Search visits the “breadth” first, i.e. if it is visiting a node then after visiting that node, it will visit the neighbor nodes (children) first before moving on to the next level neighbors.
Initially : If BFS starts at node Q, it first visits Q and puts Q in the Queue. So, Queue contains : Q. And, Visiting Order yet is : Q.
Now it dequeues Q, and explores its neighbors, which are {M,N,P}. It checks for those neighbors of Q which are not visited yet, then it visits them, and puts them in Queue (so that later their neighbors can be visited).
Now, these neighbors can be visited and put them in Queue in any order (depends on the implementation). Suppose it visits and put them in the Queue in the order ( M N P ) with M being at the FRONT and P at the REAR.
So, Visiting Order : QMNP. Now, it looks for the next entry in Queue. As Queue follows FIFO principle, M gets dequeued.
Queue contains : ( N P ) It explores M, finds its neighbors { N, Q, R }, but before visiting them it checks whether these have been visited earlier, it will only visit and put those nodes in the Queue which are not visited yet. As N and Q have been visited earlier, it will only visit R and enqueue it.
Visiting Order : QMNPR. Queue contains : ( N P R ). Now, N gets dequeued. Queue contains : ( P R ).
It explores N, finds its neighbors { M, O, Q }. As M and Q have been visited earlier, it will only visit and enqueue O. Visiting Order : QMNPRO. Queue contains : ( P R O ). Now, P gets dequeued.
Queue contains : (R O). It explores P, finds its neighbors { O, Q }. As O and Q have been visited earlier, it will NOT enqueue . Now, R gets dequeued.
Queue contains : (O). It explores R, finds its neighbor { M }. As M has been visited earlier, it will NOT enqueue.
Now, O gets dequeued. Queue contains : ( ) . It explores O, finds its neighbors { N, P }. As both have been visited earlier, it will NOT enqueue.
Now Queue is empty, hence BFS stops here. And the visiting order has been : QMNPRO.
Q. The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity (GATE Paper-2008)
θ(n)
θ(m)
θ(m + n)
θ(mn)
Ans . (3)
Explaination :
Number of connected components in undirected graph can simply calculated by doing a BFS or DFS. The best possible time complexity of BFS and DFS is O(m + n).
Q. Dijkstra’s single source shortest path algorithm when run from vertex a in the below graph, computes the correct shortest path distance to
only vertex a
only vertices a, e, f, g, h
only vertices a, b, c, d
all the vertices
Ans . (4)
Explaination :
Dijkstra’s single source shortest path is not guaranteed to work for graphs with negative weight edges, but it works for the given graph.
Let us run the 1st pass b 1 b is minimum, so shortest distance to b is 1.
After 1st pass, distances are c 3, e -2. e is minimum, so shortest distance to e is -2
After 2nd pass, distances are c 3, f 0. f is minimum, so shortest distance to f is 0
After 3rd pass, distances are c 3, g 3. Both are same, let us take g. so shortest distance to g is 3.
After 4th pass, distances are c 3, h 5 c is minimum, so shortest distance to c is 3
After 5th pass, distances are h -2 h is minimum, so shortest distance to h is -2
Q.5 Let G be a weighted graph with edge weights greater than one and G' be the graph constructed by squaring the weights of edges in G.
Let T and T' be the minimum spanning trees of G and G', respectively, with total weights t and t'.
Which of the following statements is TRUE? (GATE 2012 )
(A) T' = T with total weight t' = t2
(B) T' = T with total weight t' < t2
(C) T' != T but total weight t' = t2
(D) None of the above
Ans . D
Squaring the weights of the edges in a weighted graph will not change the minimum spanning tree.
The problem would change if , equal weights for edges would have been mentioned
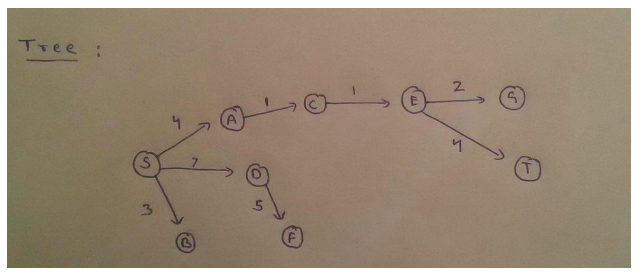
Q.8 Consider the directed graph shown in the figure below.
There are multiple shortest paths between vertices S and T. Which one will be reported by Dijstra's shortest path algorithm?
Assume that, in any iteration, the shortest path to a vertex v is updated only when a strictly shorter path to v is discovered. (GATE 2012 )
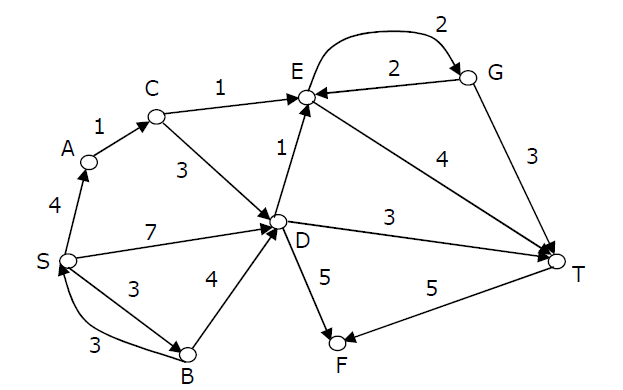
(A) SDT
(B) SBDT
(C) SACDT
(D) SACET
Ans . D
Applying Dijkstra’s algorithm to compute the shortest distances from S and finally generating the Tree as given below in the diagram.

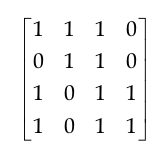
Q.An undirected graph G has n nodes. Its adjacency matrix is given by an n × n square matrix whose (i) diagonal elements are 0‘s and (ii) non-diagonal elements are 1‘s. which one of the following is TRUE?(GATE 2005)
- Graph G has no minimum spanning tree (MST)
- Graph G has a unique MST of cost n-1
- Graph G has multiple distinct MSTs, each of cost n-1
- Graph G has multiple spanning trees of different costs
Ans. 3.Graph G has multiple distinct MSTs, each of cost n-1
Solution:- If all non diagonal elements are 1, then every vertex is connected to every other vertex in the graph with an edge of weight 1. Such a graph has multiple distinct MSTs with cost n-1.
Q.4 Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.
 (GATE 2014 SET 3)
(GATE 2014 SET 3)
17
18
19
20
Ans . 18.
The following diagram shows the worst case situation where the recursion tree has maximum depth.
So the recursion depth is 19 (including the first node).
Q.1 An undirected graph C has n nodes. Its adjacency matrix is given by an n × n square matrix whose (i) diagonal elements are 0's, and (ii) non-diagonal elements are l's. Which one of the following is TRUE? (GATE 2005)
Graph G has no minimum spanning tree (MST)
Graph G has a unique MST of cost n-1
Graph G has multiple distinct MSTs, each of cost n-1
Graph G has multiple spanning trees of different costs
Ans . (c)
If all non diagonal elements are 1, then every vertex is connected to every other vertex in the graph with an edge of weight 1. Such a graph has multiple distinct MSTs with cost n-1.
Q. In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity, by (GATE 2007)
-
Dijkstra’s algorithm starting from S.
-
Warshall’s algorithm.
-
Performing a DFS starting from S
-
Performing a BFS starting from S
Ans. 4
Explanation: ( D) depends on the number of edges of the graph, and are so \(o\left(E\right)\) where E is the number of edges of the graph. (A) can be done in \(o\left(n^{2}+E\right)\) time where n is the number of nodes of the graph. Warshalls algorithm reduces to matrix multiplication which it is conjectured is asymptotically \(o\left(n^{2}\right)\).
Q. Consider a weighted complete graph G on the vertex set {v1, v2, ..vn} such that the weight of the edge (vi, vj) is 2|i-j|. The weight of a minimum spanning tree of G is:(GATE 2006)
n — 1
2n — 2
nC2
2
Ans . (B) 2n — 2
Minimum spanning tree of such a graph is
v1
\
v2
\
v3
\
v4
.
.
.
vn
Weight of the minimum spanning tree = 2|2 – 1| + 2|3 – 2| + 2|4 – 3| + 2|5 – 4| …. + 2| n – (n-1) | = 2n – 2