ASYMMETRIC-KEY CRYPTOGRAPHY
Asymmetric-key (or public-key) cipher uses two keys: one private and one public. We discuss two algorithms: RSA and Diffie-Hellman
Rivest, Shamir, and Adleman (RSA).
Bob use the following steps to select the private and public keys:
Bob chooses two very large prime numbers p and q. Remember that a prime number is one that can be divided evenly only by 1 and itself.
Bob multiplies the above two primes to find n, the modulus for encryption and decryption. In other words, n = p * q
Bob calculates another number ϕ = (p - 1) x (q - 1).
Bob chooses a random integer e. He then calculates d so that d x e = 1 mod ϕ
Bob announces e and n to the public; he keeps ϕ and d secret.
Anyone who needs to send a message to Bob can use nand e. For example, if Alice needs to send a message to Bob, she can change the message, usually a short one, to an integer. This is the plaintext. She then calculates the ciphertext, using e and n. C=Pemod n ; Alice sends C, the ciphertext, to Bob.
Bob keeps ϕ and d private. When he receives the ciphertext, he uses his private key d to decrypt the message: p= Cd(modn)
For RSA to work, the value of P must be less than the value of n. If P is a large number, the plaintext needs to be divided into blocks to make P less than n.
Although RSA can be used to encrypt and decrypt actual messages, it is very slow if the message is long.
RSA, therefore, is useful for short messages such as a small message digest or a symmetric key to be used for a symmetric-key cryptosystem.
In particular, we will see that RSA is used in digital signatures and other cryptosystems that often need to encrypt a small message without having access to a symmetric key.
RSA is also used for authentication
Q. Bob chooses 7 and 11 as p and q and calculates n = 7 . 11 = 77. The value of ϕ = (7 - 1) (11 - 1) or 60. Now he chooses two keys, e and d. If he chooses e to be 13, then dis 37. Now imagine Alice sends the plaintext 5 to Bob. She uses the public key 13 to encrypt 5.
Plaintext: 5
C = 513 = 26 mod 71; Ciphertext: 26
Bob receives the ciphertext 26 and uses the private key 37 to decipher the ciphertext:
Ciphertext: 26; P = 2637 = 5 mod 77; Plaintext: 5; The plaintext 5 sent by Alice is received as plaintext 5 by Bob
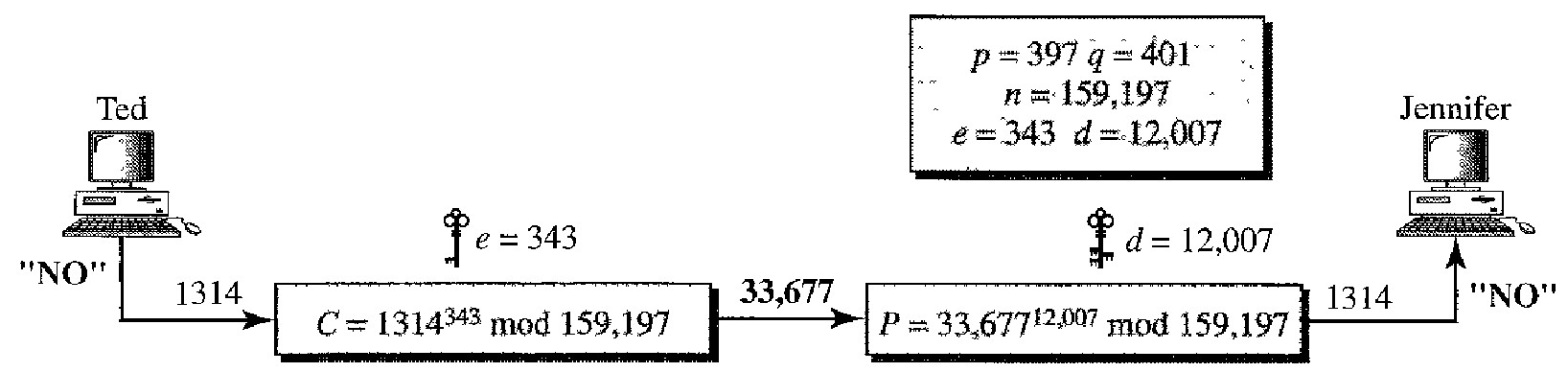
Q. Jennifer creates a pair of keys for herself. She chooses p = 397 and q = 401. She calculates n = 159,197 and ϕ = 396 . 400 = 158,400. She then chooses e = 343 and d = 12,007. Show how Ted can send a message to Jennifer if he knows e and n.
Suppose Ted wants to send the message "NO" to Jennifer. He changes each character to a number (from 00 to 25) with each character coded as two digits. He then concatenates the two coded characters and gets a four-digit number.
The plaintext is 1314. Ted then uses e and n to encrypt the message. The ciphertext is 1314343 = 33,677 mod 159,197.
Jennifer receives the message 33,677 and uses the decryptionkey d to decipheritas 33,67712,007 = 1314 mod 159,197.Jennifer then decodes 1314 as the message "NO".
Diffie- Hellman
RSA is a public-key cryptosystem that is often used to encrypt and decrypt symmetric keys. Diffie-Hellman, on the other hand, was originally designed for key exchange. In the Diffie-Hellman cryptosystem, two parties create a symmetric session key to exchange data without having to remember or store the key for future use.
They do not have to meet to agree on the key; it can be done through the Internet.
Before establishing a symmetric key, the two parties need to choose two numbers p and g.
The first number, p, is a large prime number on the order of 300 decimal digits (1024 bits). The second number is a random number. These two numbers need not be confidential They can be sent through the Internet; they can be public.
Step 1: Alice chooses a large random number x and calculates R1 = gx mod p.
Step 2: Bob chooses another large random number y and calculates R2 = gY mod p.
Step 3: Alice sends R1 to Bob. Note that Alice does not send the value of x; she sends only R1.
Step 4: Bob sends R2 to Alice. Again, note that Bob does not send the value of y, he sends only R2
Step 5: Alice calculates K = R2X mod p.
Step 6: Bob also calculates K = (R1)Y mod p.
Bob has calculated K = (R1)Y mod p = (gx mod p)Y mod p = gXY mod p. Alice has calculated K = (R2)X mod p = (gY mod p)X mod = gXY mod p. Both have reached the same value without Bob knowing the value of x and without Alice knowing the value of y.
The symmetric (shared) key in the Diffie-Hellman protocol is K = gXY mod p.
Q. Let us give a trivial example to make the procedure clear. Our example uses small numbers, but note that in a real situation, the numbers are very large. Assume g = 7 and p = 23. The steps are as follows:
Alice chooses x = 3 and calculates R1 = 73 mod 23 = 21.
Bob chooses y = 6 and calculates R2 = 76 mod 23 = 4.
Alice sends the number 21 to Bob. Bob sends the number 4 to Alice.
Alice calculates the symmetric key K = 43 mod 23 = 18. Bob calculates the symmetric key K = 216 mod 23 = 18. The value of K is the same for both Alice and Bob; gxy mod p = 718 mod 23 = 18.
Idea of Diffie-Hellman
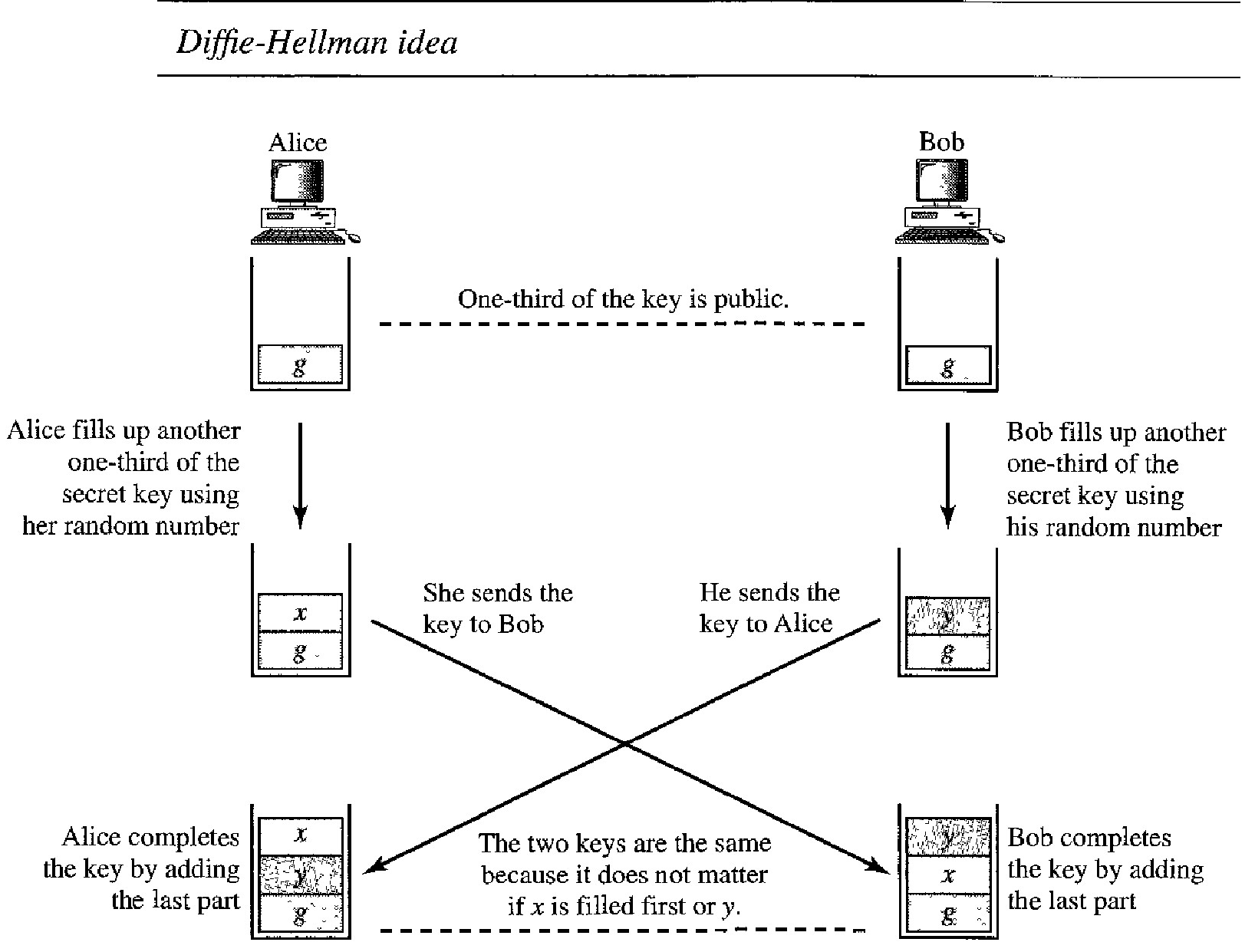
We can think of the secret key between Alice and Bob as made of three parts: g, x, and y.
The first part is public. Everyone knows one-third of the key; g is a public value.
The other two parts must be added by Alice and Bob. Each adds one part.
Alice adds x as the second part for Bob; Bob adds y as the second part for Alice.
When Alice receives the two-thirds completed key from Bob, she adds the last part, her x, to complete the key.
When Bob receives the two-thirds completed key from Alice, he adds the last part, his y, to complete the key.
Note that although the key in Alice's hand consists of g-y-x and the key in Bob's hand is g-x-y, these two keys are the same because gxy = gyx. Note also that although the two keys are the same, Alice cannot find the value y used by Bob because the calculation is done in modulo p; Alice receives gY mod p from Bob, not gY.
Man in the middle attack on Diffie helman
If x and y are very large numbers, it is extremely difficult for Eve to find the key, knowing only p and g.
An intruder needs to determine x and y if Rl and R2 are intercepted. But finding x from Rl and y from R2 are two difficult tasks.
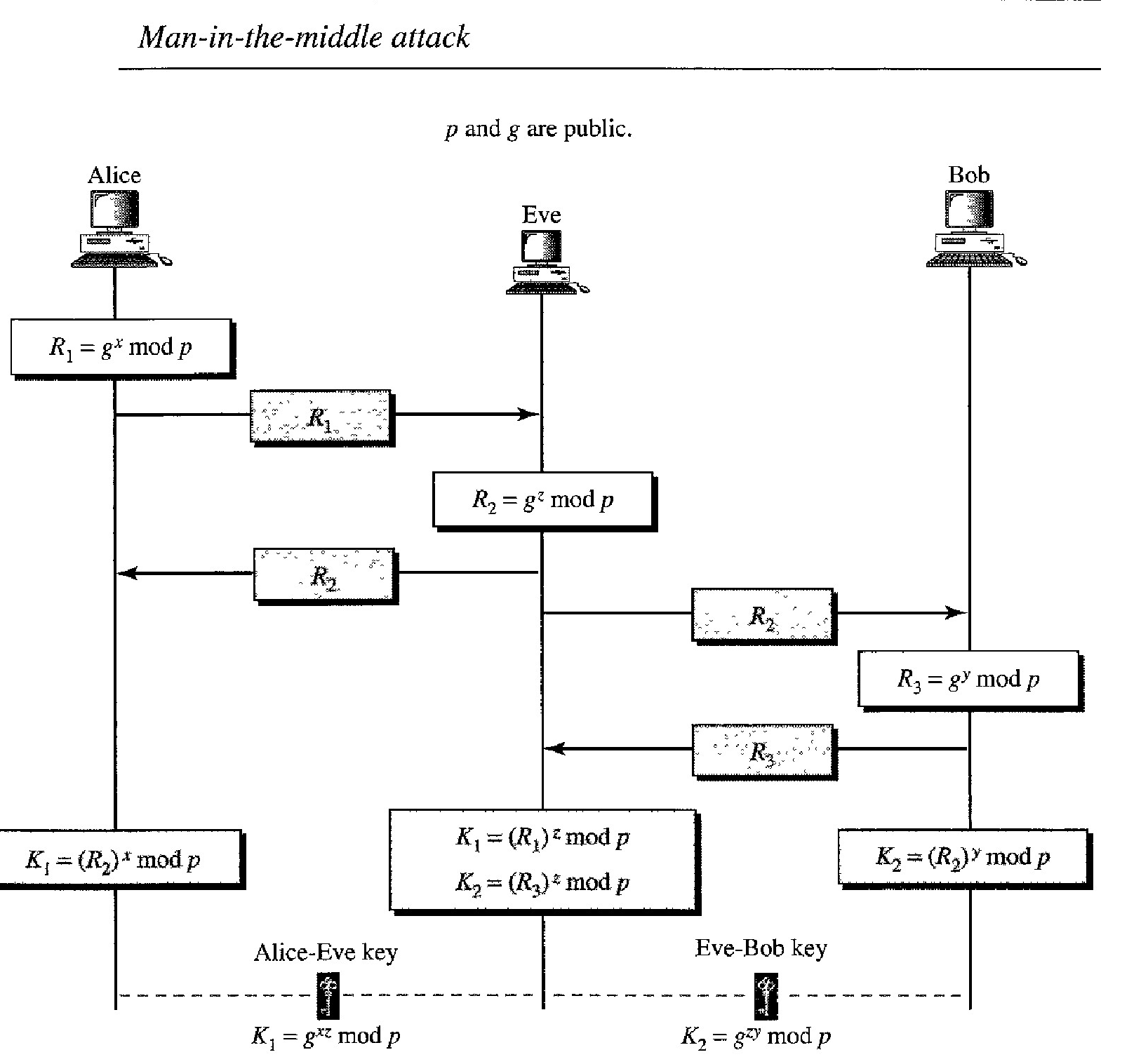
However, the protocol does have a weakness. Eve does not have to find the value of x and y to attack the protocol. She can fool Alice and Bob by creating two keys: one between herself and Alice and another between herself and Bob.
The following can happen:
Alice chooses x, calculates Rl = gx mod p, and sends Rl to Bob. Eve, the intruder, intercepts R1 She chooses z, calculates R2 = gz mod p, and sends R2 to both Alice and Bob.
Bob chooses y, calculates R3 = gY mod p, and sends R3 to Alice; R3 is intercepted by Eve and never reaches Alice.
Alice and Eve calculate K1 = gxz mod p, which becomes a shared key between Alice and Eve. Alice, however, thinks that it is a key shared between Bob and herself.
Eve and Bob calculate K2 = gZY mod p, which becomes a shared key between Eve and Bob. Bob, however, thinks that it is a key shared between Alice and himself.
In other words, two keys, instead of one, are created: one between Alice and Eve and one between Eve and Bob.
When Alice sends data to Bob encrypted with Kl (shared by Alice and Eve), it can be deciphered and read by Eve.
Eve can send the message to Bob encrypted by K2 (shared key between Eve and Bob); or she can even change the message or send a totally new message.
Bob is fooled into believing that the message has come from Alice.
A similar scenario can happen to Alice in the other direction.
This situation is called a man-in-the-middle attack because Eve comes in between and intercepts R1 sent by Alice to Bob, and R3, sent by Bob to Alice.
It is also known as a bucket brigade attack because it resembles a short line of volunteers passing a bucket of water from person to person.
SECURITY SERVICES
Network security can provide one of the five services. Four of these services are related to the message exchanged using the network: message confidentiality, integrity, authentication, and nonrepudiation. The fifth service provides entity authentication or identification.
Message Confidentiality : Message confidentiality or privacy means that the sender and the receiver expect confidentiality. The transmitted message must make sense to only the intended receiver. To all others, the message must be garbage. When a customer communicates with her bank, she expects that the communication is totally confidential.
Message Integrity : Message integrity means that the data must arrive at the receiver exactly as they were sent. There must be no changes during the transmission, neither accidentally nor maliciously. As more and more monetary exchanges occur over the Internet, integrity is crucial. For example, it would be disastrous if a request for transferring $100 changed to a request for $10,000 or $100,000. The integrity of the message must be preserved in a secure communication.
Message Authentication : Message authentication is a service beyond message integrity. In message authentication the receiver needs to be sure of the sender's identity and that an imposter has not sent the message.
Message Nonrepudiation : Message nonrepudiation means that a sender must not be able to deny sending a message that he or she, in fact, did send. The burden of proof falls on the receiver. For example, when a customer sends a message to transfer money from one account to another, the bank: must have proof that the customer actually requested this transaction.
Entity Authentication : In entity authentication (or user identification) the entity or user is verified prior to access to the system resources (files, for example). For example, a student who needs to access her university resources needs to be authenticated during the logging process. This is to protect the interests of the university and the student.
Confidentiality with Symmetric-Key Cryptography
To provide confi- dentiality with symmetric-key cryptography, a sender and a receiver need to share a secret key.
To be able to use symmetric-key cryptography, we need to find a solution to the key sharing. This can be done using a session key. A session key is one that is used only for the duration of one session. The session key itself is exchanged using asymmetrickey cryptography
Note that the nature of the symmetric key allows the communication to be carried on in both direc- tions although it is not recommended today.
Using two different keys is more secure, because if one key is compromised, the communication is still confidential in the other direction. The reason symmetric-key cryptography is still the dominant method for confidentiality of the message is its efficiency. For a long message, symmetric-key cryptography is much more efficient than asymmetric-key cryptography.
Confidentiality with asymmetric-key cryptosystem has its own problems. First, the method is based on long mathematical calculations using long keys.
This means that this system is very inefficient for long messages; it should be applied only to short messages. Second, the sender of the message still needs to be certain about the public key of the receiver.
For example, in Alice-Bob communication, Alice needs to be sure that Bob's public key is genuine; Eve may have announced her public key in the name of Bob.
MESSAGE INTEGRITY
Encryption and decryption provide secrecy, or confidentiality, but not integrity. However, on occasion we may not even need secrecy, but instead must have integrity. For example, Alice may write a will to distribute her estate upon her death. The will does not need to be encrypted.
After her death, anyone can examine the wilL The integrity of the will, however, needs to be preserved. Alice does not want the contents of the will to be changed. As another example, suppose Alice sends a message instructing her banker, Bob, to pay Eve for consulting work.
The message does not need to be hidden from Eve because she already knows she is to be paid. However, the message does need to be safe from any tampering, especially by Eve.
One way to preserve the integrity of a document is through the use of a fingerprint. If Alice needs to be sure that the contents of her document will not be illegally changed, she can put her fingerprint at the bottom of the document.
Eve cannot modify the contents of this document or create a false document because she cannot forge Alice's fingerprint. To ensure that the document has not been changed, Alice's fingerprint on the document can be compared to Alice's fingerprint on file. If they are not the same, the document is not from Alice.
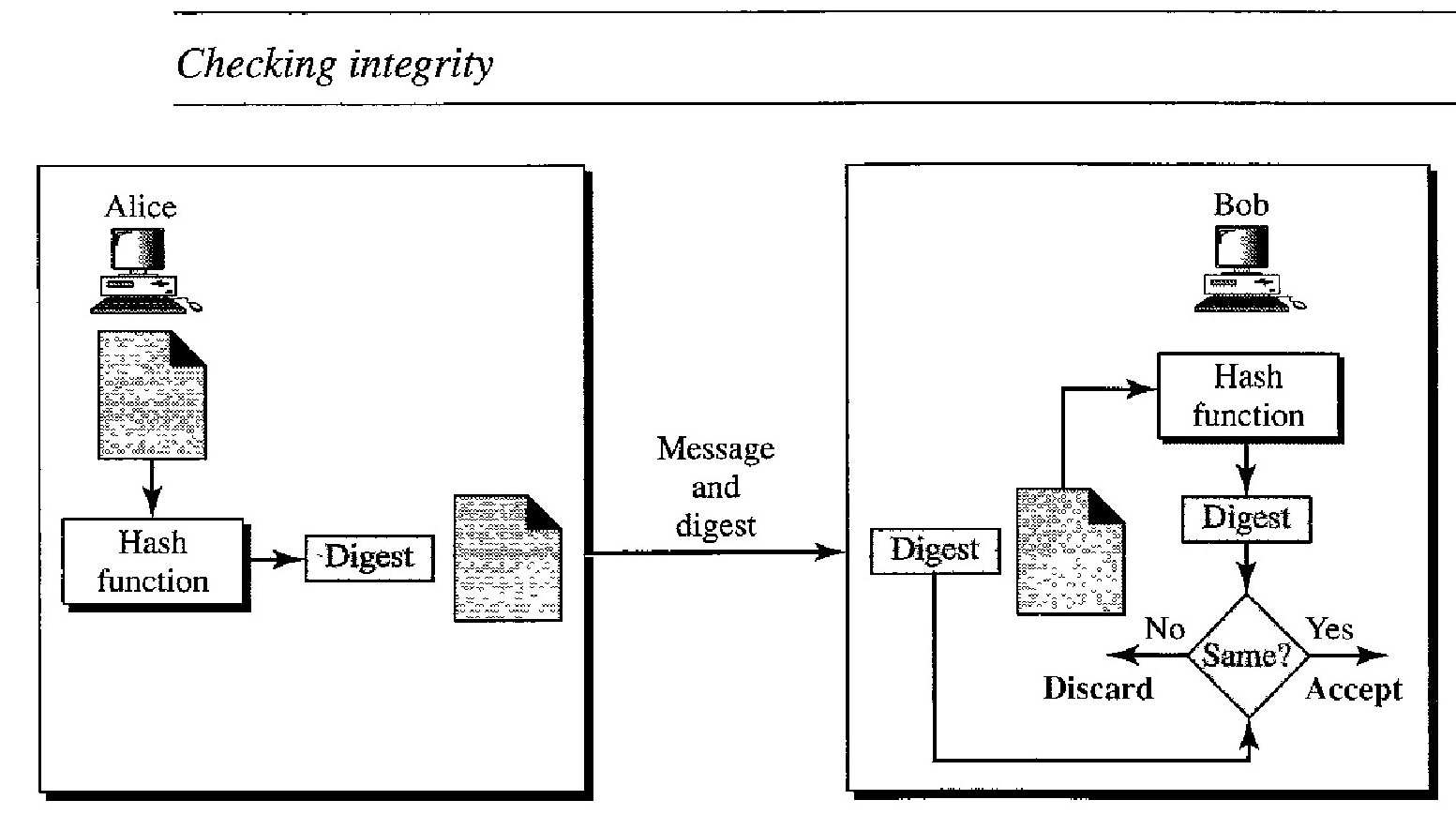
The electronic equivalent of the document and fingerprint pair is the message and message digest pail: To preserve the integrity of a message, the message is passed through an algorithm called a hash function. The hash function creates a compressed image of the message that can be used as a fingerprint. Figure below shows the message, hash function, and the message digest.
The two pairs document/fingerprint and message/message digest are similar, with some differences. The document and fingerprint are physically linked together; also, neither needs to be kept secret.
The message and message digest can be unlinked (or sent) sep- arately and, most importantly, the message digest needs to be kept secret. The message digest is either kept secret in a safe place or encrypted if we need to send it through a communications channel.
The message digest is created at the sender site and is sent with the message to the receiver. To check the integrity of a message, or document, the receiver creates the hash function again and compares the new message digest with the one received.
If both are the same, the receiver is sure that the original message has not been changed. Of course, we are assuming that the digest has been sent secretly. Figure below shows the idea.
To be eligible for a hash, a function needs to meet three criteria: one-wayness, resistance to weak collision, and resistance to strong collision. A hash function must have one-wayness; a message digest is created by a one-way hashing function. We must not be able to recreate the message from the digest.
Sometimes it is difficult to make a hash function 100 percent one-way; the criteria state that it must be extremely difficult or impossible to create the message if the message digest is given. This is similar to the document/fingerprint case.
No one can make a document from a fingerprint. The second criterion, weak collision resistance, ensures that a message cannot easily be forged.
If Alice creates a message and a digest and sends both to Bob, this criterion ensures that Eve cannot easily create another message that hashes exactly to the same digest.
In other words, given a specific message and its digest, it is impossible (or at least very difficult) to create another message with the same digest.
When two messages create the same digest, we say there is a collision. In a weak collision, given a message digest, it is very unlikely that someone can create a message with exactly the same digest.
A hash function must have weak collision resistance. The third criterion, strong collision resistance, ensures that we cannot find two messages that hash to the same digest.
This criterion is needed to ensure that Alice, the sender of the message, cannot cause problems by forging a message.
If Alice can create two messages that hash to the same digest, she can deny sending the first to Bob and claim that she sent only the second.
This type of collision is called strong because the probability of collision is higher than in the previous case. An adversary can create two messages that hash to the same digest.
For example, if the number of bits in the message digest is small, it is likely Alice can create two different messages with the same message digest. She can send the first to Bob and keep the second for herself.
Alice can later say that the second was the original agreed-upon document and not the first.
Suppose two different wills can be created that hash to the same digest. When the time comes for the execution of the will, the second will is presented to the heirs.
Since the digest matches both wills, the substitution is successful.
MESSAGE AUTHENTICATION
A hash function guarantees the integrity of a message. It guarantees that the message has not been changed.
A hash function, however, does not authenticate the sender of the message. When Alice sends a message to Bob, Bob needs to know if the message is coming from Alice or Eve.
To provide message authentication, Alice needs to provide proof that it is Alice sending the message and not an imposter. A hash function per se cannot provide such a proof.
The digest created by a hash function is normally called a modification detection code (MDC). The code can detect any modification in the message.
To provide message authentication, we need to change a modification detection code to a message authentication code (MAC). An MDC uses a keyless hash function; a MAC uses a keyed hash function.
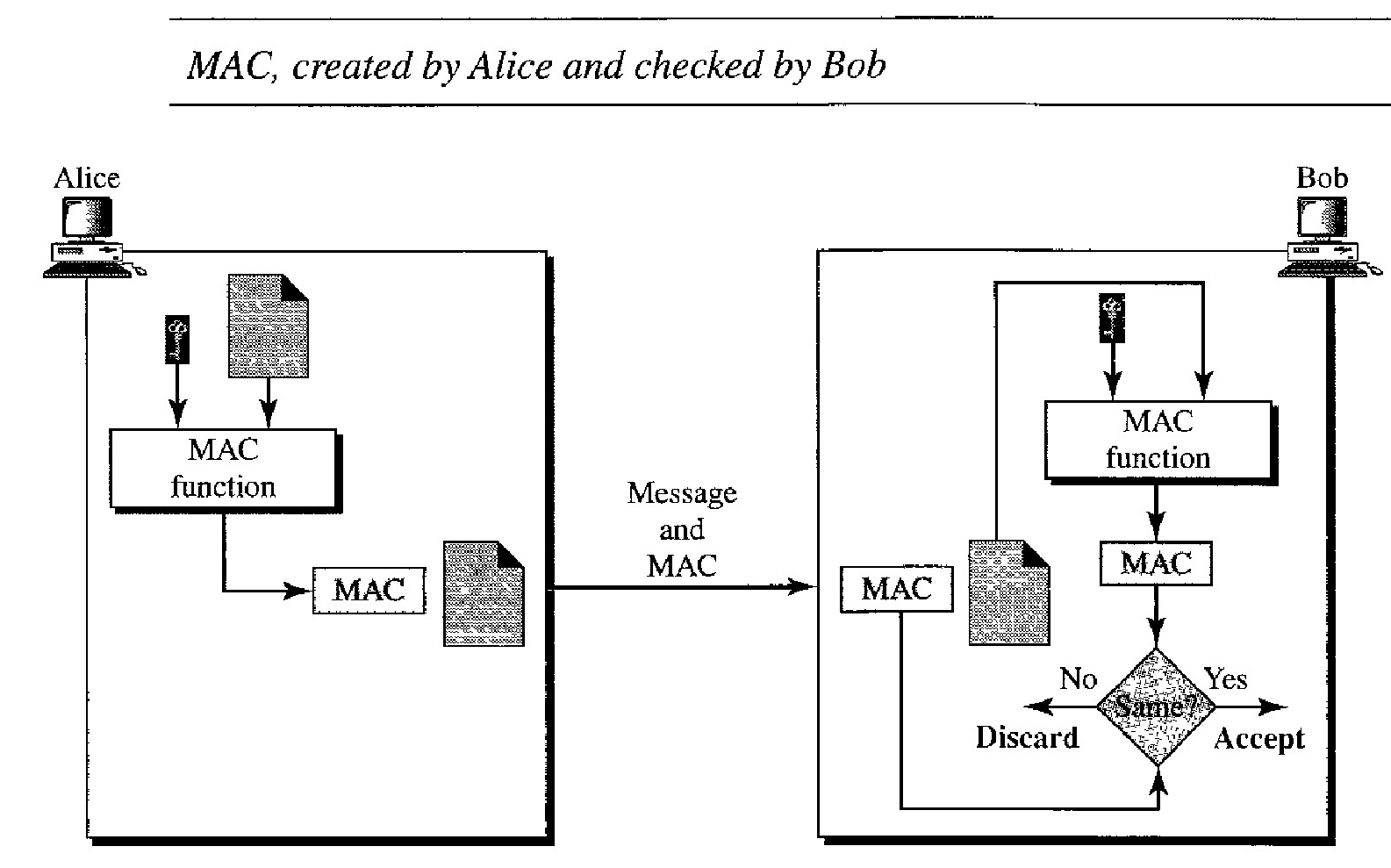
A keyed hash function includes the symmetric key between the sender and receiver when creating the digest.
Alice, using the symmetric key between herself and Bob (KAB) and a keyed hash function, generates a MAC.
She then concatenates the MAC with the original message and sends the two to Bob.
Bob receives the message and the MAC. He separates the message from the MAC.
He applies the same keyed hash function to the message using the symmetric key KAB to get a fresh MAC. He then compares the MAC sent by Alice with the newly generated MAC.
If the two MACs are identical, the message has not been modified and the sender of the message is definitely Alice.
DIGITAL SIGNATURE
Although a MAC can provide message integrity and message authentication, it has a drawback.
It needs a symmetric key that must be established between the sender and the receiver.
A digital signature, on the other hand, can use a pair of asymmetric keys (a public one and a private one).
We are all familiar with the concept of a signature. We sign a document to show that it originated from us or was approved by us.
The signature is proof to the recipient that the document comes from the correct entity. When a customer signs a check to himself, the bank needs to be sure that the check is issued by that customer and nobody else.
In other words, a signature on a document, when verified, is a sign of authentication; the document is authentic. Consider a painting signed by an artist. The signature on the art, if authentic, means that the painting is probably authentic.
When Alice sends a message to Bob, Bob needs to check the authenticity of the sender; he needs to be sure that the message comes from Alice and not Eve. Bob can ask Alice to sign the message electronically.
In other words, an electronic signature can prove the authenticity of Alice as the sender of the message. We refer to this type of signature as a digital signature.
Signing the Document
Digital signature can be achieved in two ways: signing the document or signing a digest of the document.
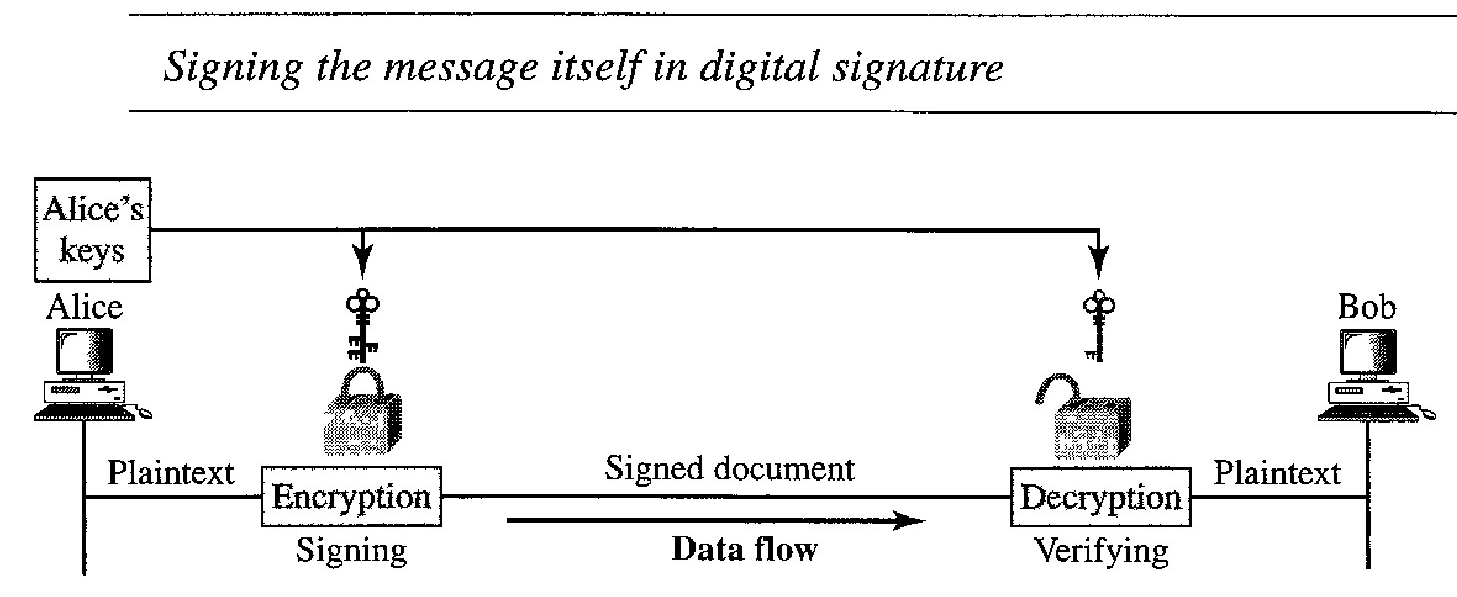
Probably, the easier, but less efficient way is to sign the document itself. Signing a doc- ument is encrypting it with the private key of the sender; verifying the document is decrypting it with the public key of the sender.
We should make a distinction between private and public keys as used in digital signature and public and private keys as used for confidentiality.
In the latter, the private and public keys of the receiver are used in the process. The sender uses the public key of the receiver to encrypt; the receiver uses his own private key to decrypt.
In digital signature, the private and public keys of the sender are used. The sender uses her pri- vate key; the receiver uses the public key of the sender.
Solved Question Papers
Public key is very inefficient in a cryptosystem if we are dealing with long messages. In a digital signature system, our messages are normally long, but we have to use public keys.
The solution is not to sign the message itself; instead, we sign a digest of the message.
As we learned, a carefully selected message digest has a one-to-one relationship with the message. The sender can sign the message digest, and the receiver can verify the message digest. The effect is the same.
A digest is made out of the message at Alice's site. The digest then goes through the signing process using Alice's private key. Alice then sends the message and the signature to Bob.
At Bob's site, using the same public hash function, a digest is first created out of the received message. Calculations are done on the signature and the digest. The verifying process also applies criteria on the result of the calculation to determine the authenticity of the signature. If authentic, the message is accepted; otherwise, it is rejected.
Note that a digital signature scheme does not provide confidential communication.
The integrity of the message is preserved even if we sign the whole message because we cannot get the same signature if the message is changed.
The signature schemes today use a hash function in the signing and verifying algorithms that preserve the integrity of the message.
A secure signature scheme, like a secure conventional signature (one that cannot be easily copied), can provide message authentication.
Bob can verify that the message is sent by Alice because Alice's public key is used in verification. Alice's public key cannot create the same signature as Eve's private key.
Alice creates a signature from her message (SA) and sends the message, her identity, Bob's identity, and the signature to the third party trusted center.
The center, after checking that Alice's public key is valid, verifies through Alice's public key that the message comes from Alice.
The center then saves a copy of the message with the sender identity, recipient identity, and a timestamp in its archive. The center uses its private key to create another signature (ST) from the message.
The center then sends the message, the new signature, Alice's identity, and Bob's identity to Bob. Bob verifies the message using the public key of the trusted center.
If in the future Alice denies that she has sent the message, the center can show a copy of the saved message. If Bob's message is a duplicate of the message saved at the center, Alice will lose the dispute.
FIREWALLS
All previous security measures cannot prevent Eve from sending a harmful message to a system. To control access to a system, we need firewalls.
A firewall is a device (usually a router or a computer) installed between the internal network of an organization and the rest of the Internet.
It is designed to forward some packets and filter (not forward) others.
For example, a firewall may filter all incoming packets destined for a specific host or a specific server such as HTTP. A firewall can be used to deny access to a specific host or a specific service in the organization. A firewall is usually classified as a packet-filter firewall or a proxy-based firewall.
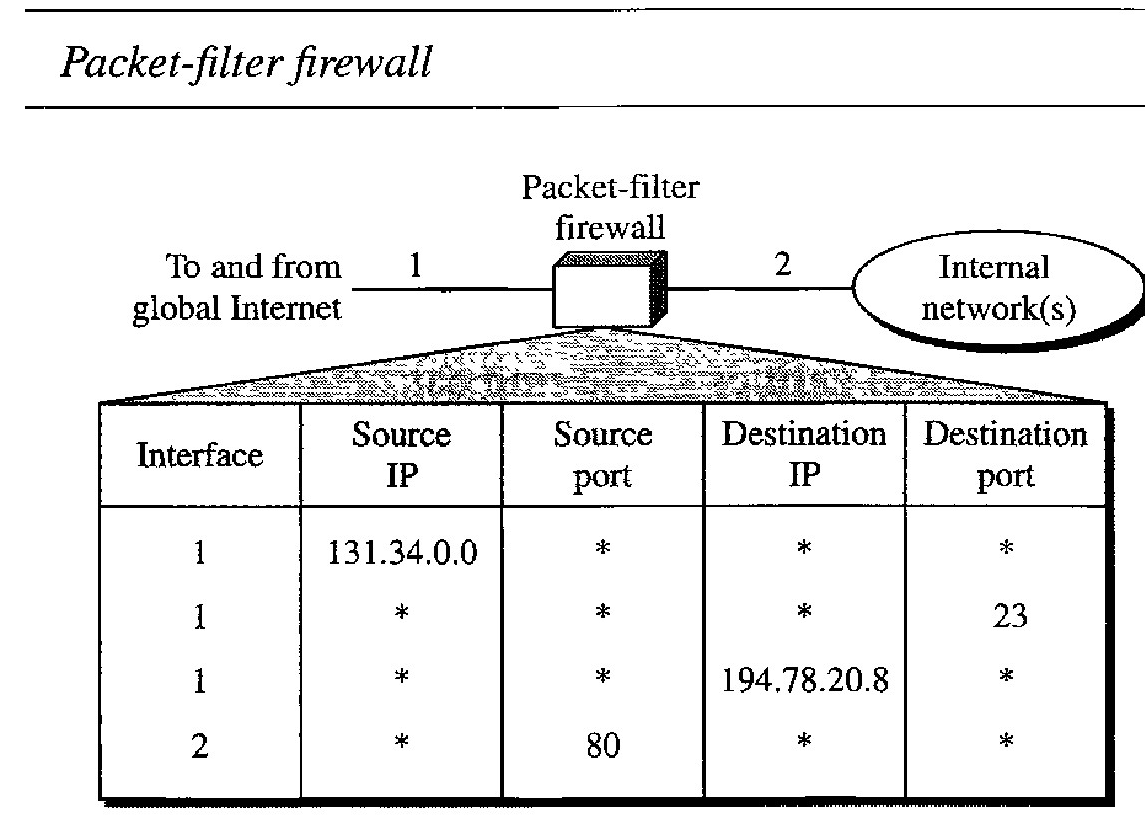
Packet- Filter Firewall : A firewall can be used as a packet filter. It can forward or block packets based on the information in the network layer and transport layer headers: source and destination IP addresses, source and destination port addresses, and type of protocol (TCP or UDP). A packet-filter firewall is a router that uses a filtering table to decide which packets must be discarded (not forwarded).
According to Figure above, the following packets are filtered : Incoming packets from network 131.34.0.0 are blocked (security precaution). Note that the * (asterisk) means "any."
Incoming packets destined for any internal TELNET server (port 23) are blocked. Incoming packets destined for internal host 194.78.20.8 are blocked. The organiza- tion wants this host for internal use only
Outgoing packets destined for an HTIP server (port 80) are blocked. The organi- zation does not want employees to browse the Internet.
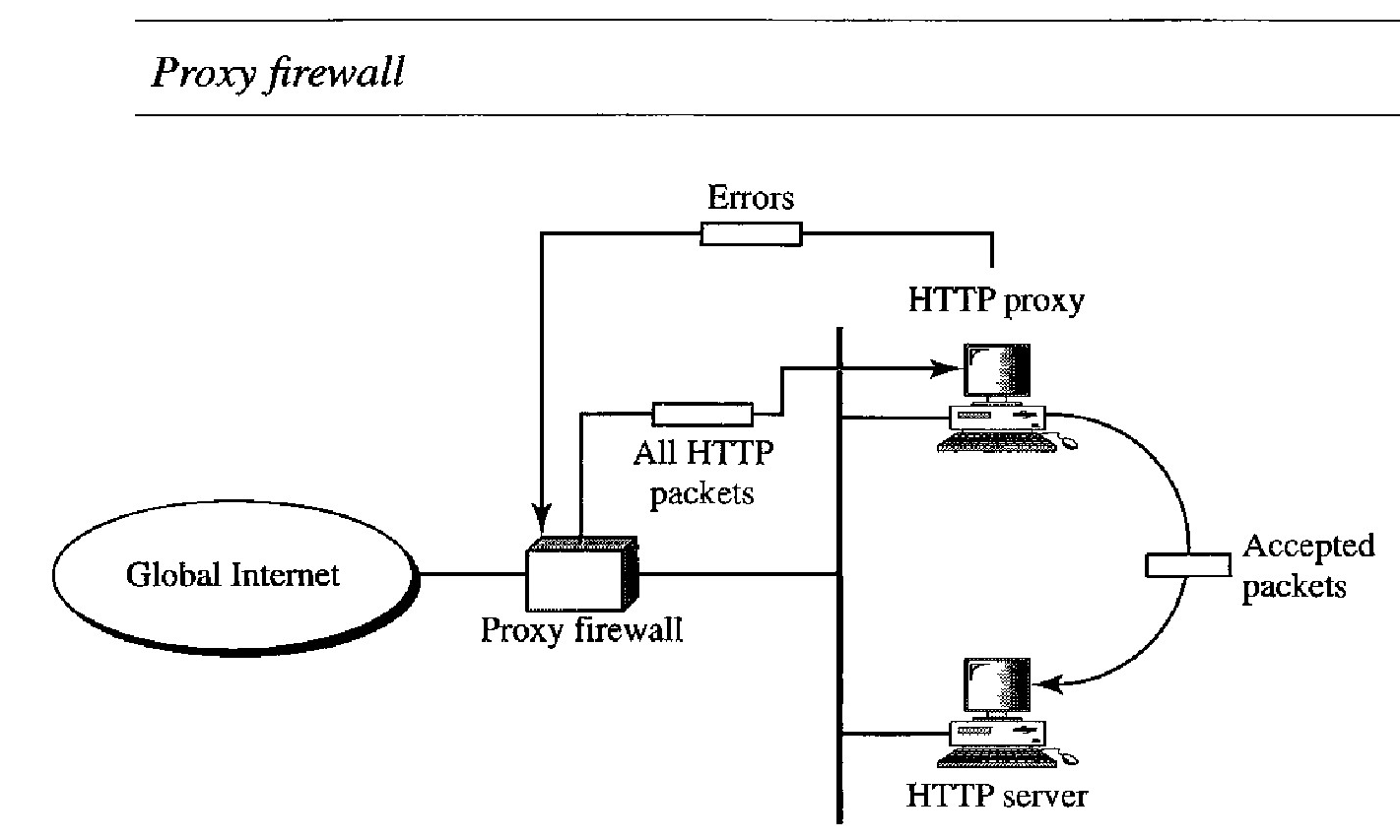
Proxy Firewall - A proxy firewall filters at the application layer.
The packet-filter firewall is based on the information available in the network layer and transport layer headers (IP and TCP / UDP).
However, sometimes we need to filter a message based on the information available in the message itself (at the application layer).
As an example, assume that an organization wants to implement the following policies regarding its Web pages: Only those Internet users who have previously estab- lished business relations with the company can have access; access to other users must be blocked.
In this case, a packet-filter firewall is not feasible because it cannot distinguish between different packets arriving at TCP port 80 (HTTP). Testing must be done at the application level (using URLs).
One solution is to install a proxy computer (sometimes called an application gateway), which stands between the customer (user client) computer and the corporation computer
When the user client process sends a message, the proxy firewall runs a server process to receive the request.
The server opens the packet at the application level and finds out if the request is legitimate.
If it is, the server acts as a client process and sends the message to the real server in the corporation.
If it is not, the message is dropped and an error message is sent to the external user.
In this way, the requests of the external users are filtered based on the contents at the application layer