A Moore machine is a collection of five things:

A finite set of states \( q_0, q_1 , q_2 . . . \) where q₀ is designated as the start state.

An alphabet of letters for forming the input string Σ = {a, b, c. .... .}

An alphabet of possible output characters Γ = {x, y, z ... }.

A transition table that shows for each state and each input letter what state is reached next.

An output table that shows what character from Γ is printed by each state that is entered.

Notice that we did not assume that the input alphabet Σ is the same as the output alphabet Γ. When dealing with twentieth-century machines, both input and output are usually encoded strings of 0's and 1's. However, we may interpret the input bit strings as instructions in a programming language.

To keep the output alphabet separate from the input alphabet, we give it a different name, Γ instead of Σ, and for its letters we use symbols from the other end of the Latin alphabet: {x, y, z . .. } or numbers {0, 1 . .. } instead of {a, b, c ... }.

Moreover, we refer to the input symbols (as we always have) as letters, while we call the output symbols characters.

As we shall see from our circuitry examples, the knowledge of which state is the start state is not always important in applications.

If the machine is run several times, it may continue from where it left off rather than restart.

Because of this, we can define the Moore machine in two ways: Either the first symbol printed is the character always specified in the start state or else it is the character specified in the next state, which is the first state chosen.

We shall adopt the policy that a Moore machine always begins by printing the character dictated by the mandatory start state.

If the input string has 7 letters, then the output string will have 8 characters because it includes eight states in its path.

A Moore machine does not define a language of accepted words, since every input string creates an output string and there is no such thing as a final state.

The processing is terminated when the last input letter is read and the last output character is printed.

Moore machines have pictorial representations very similar to their cousins the FA's. We start with little circles depicting the states and directed edges between them labeled with input letters.

The difference is that instead of having only the name of the state inside the little circle, we also specify the output character printed by that state.

The two symbols inside the circle are separated by a slash "/". On the left side is the name of the state and on the right is the output from that state

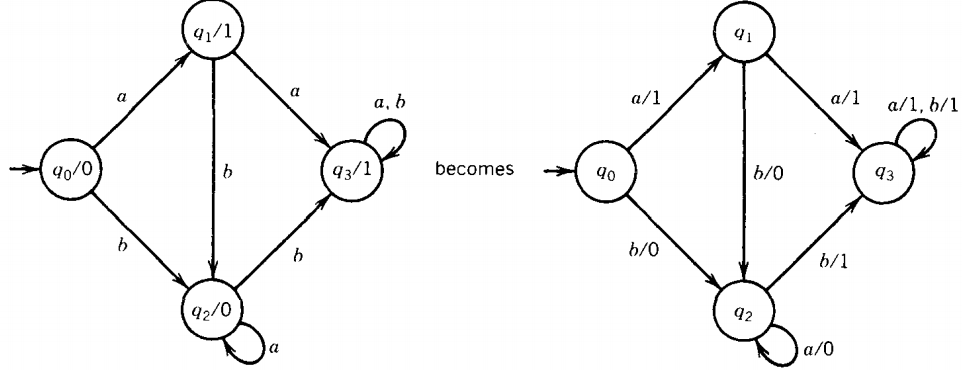
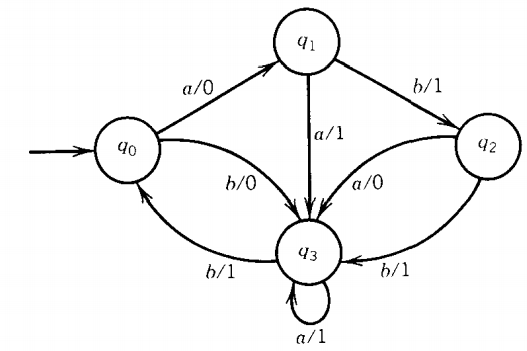
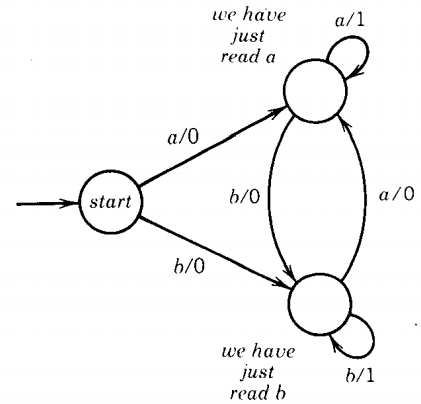
Q. Let us consider an example defined first by a table:
Input alphabet: Σ = {a, b}
Output alphabet: Γ = {0, 1}
Names of states: \( q_0, q_1 , q_2 , q_3 \) , (q₀ = start state)

The pictorial representation of this Moore machine is

In Moore machines, so much information is written inside the state circles that there is no room for the minus sign indicating the start state.

We usually indicate the start state by an outside arrow as shown above.

As mentioned before there is no need for any plus signs either, since any input string will generate an output string and can end in any state having done an acceptable job.

Let us trace the operation of this machine on the input string abab. We always start this machine off in start qo, which automatically prints out the character 1.

We then read the first letter of the input string, which is an a and which sends us to state q1.

This state tells us to print a 0. The next input letter is a b, and the loop shows that we return to state q1.

Being in q, again, we print another 0.

Then we read an a, go to q3, and print a 1. Next we read a b, go to q2, and print a 0. This is the end of the run. The output sequence has been 10010.

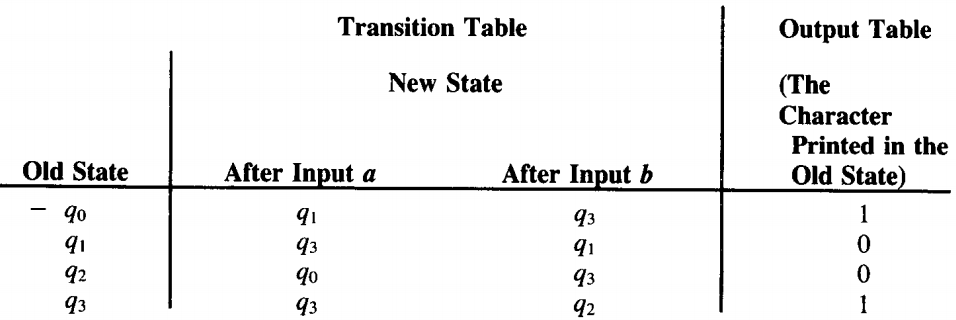
Q. Suppose we were interested in knowing exactly how many times the substring aab occurs in a long input string. The following Moore machine will "count" this for us:

Every state of this machine prints out the character 0 except for state q3, which prints a 1.

To get to state q3, we must have come from state q2 and have just read a b.

To get to state q2, we must have just read at least two a's in a row, having started in any state.

After finding the substring aab and tallying a 1 for it, we begin to look for the next aab.

If we read a b, we start the search in q0; if we read an a, we start in q1.

The number of substrings aab in the input string will be exactly the number of l's in the output string.

To count up how many 1's are in the output string we could use bit collection methods from assembly-language programming, depending on the application we have in mind.

The example above is part of a whole class of useful Moore machines.

Given a language L and an FA that accepts it, if we add the printing instruction 0 to any nonfinal state and 1 to each final state

The 1's in any output sequence mark the end position of all substrings of the input string starting from the first letter that are words in L.

The machine above with q0 = - , q3 = + accepts all words that end in aab

A Mealy machine is like a Moore machine except that now we do our printing while we are traveling along the edges, not in the states themselves.

If we are in state q4 and we are proceeding to q7 , we do not simply print what q7 tells us.

What we print depends on the edge we take. If there are two different edges from q4 to q7, one an a-edge and one a b-edge, it is possible that they will have different printing instructions for us.

We take no printing instructions from the state itself

A Mealy machine is a collection of four things:

A finite set of states \( q_0, q_1 , q_2 . . . \) where q₀ is designated as the start state.

An alphabet of letters for forming the input string Σ = {a, b, c. .... .}

An alphabet of possible output characters Γ = {x, y, z ... }.

A pictorial representation with states represented by small circles and directed edges indicating transitions between states. Each edge is labeled with a compound symbol of the form i/o where i is an input letter and o is an output character. Every state must have exactly one outgoing edge for each possible input letter The edge we travel is determined by the input letter i; while traveling on the edge we must print the output character o.

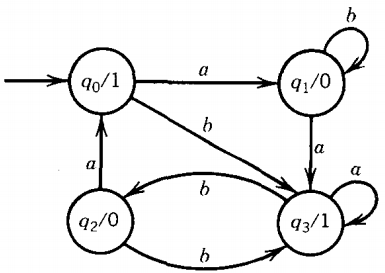
The following picture represents a Mealy machine:

Notice that when we arrive in state q3 we may have just printed a 1 or a 0.

If we came from state q0 by the b-road, we printed a 0. If we got there from q, by the a-road, we printed a 1.

If we got there from q2, it depends on whether we took the a-road and printed a 0 or the b-road and printed a 1. If we were in q3 before and looped back on the input a, we then printed a 1.

Every time we enter q, we have just printed a 0, but it is not always possible to tell this information from the destination state alone.

Let us trace the running of this machine on the input sequence aaabb.

We start in state q0. In distinction to the Moore machine, here we do not have to print the same character each time we start up, even before getting a look at the input.

The first input letter is an a, which takes us to q, and prints a 0. The second letter is an a, which takes to q3 and prints a 1.

The third letter is an a, which loops us back to q3 and prints a 1.

The fourth letter is a b, which takes us back to qo and prints a 1. The fifth letter is a b, which takes us to q3 and prints a 0. The output string for this input is 01110.

Notice that in a Mealy machine the output string has the same number of characters as the input string has letters.

As with the Moore machine, the Mealy machine does not define a language, so it has no final states. However, we will see shortly that there is a sense in which it can recognize a language.

If there are two edges going in the same direction between the same pair of states, we can draw only one arrow and represent the choice of label by the usual comma.

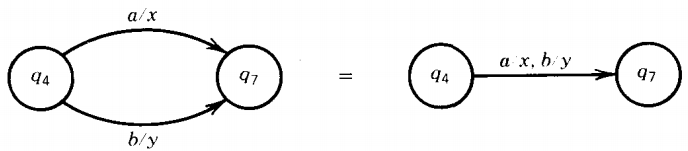
Q. A useful Mealy machine that prints' out the l's complement of an input bit string.

The simplest example of a useful Mealy machine is one that prints' out the l's complement of an input bit string.

This means that we want to produce a bit string that has a 1 wherever the input string has a 0 and a 0 wherever the input has a 1.

For example, the input 101 should become the output 010. One machine that does this is:

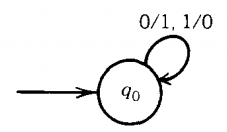
If the input is 001010 the output is 110101. This is a case where the input alphabet and output alphabet are both {0, 1}.

Q. Mealy machine called the increment machine that assumes that its input is a binary number and prints out the binary number that is one larger.

We assume that the input bit string is a binary number fed in backwards, that is, units digit first (then 2's digit, 4's digit . . . ).

The output string will be the binary representation of the number one greater and will also be generated units bit first (backwards).

The machine will have three states: start, owe-carry, no-carry. The owe-carry state represents the overflow when two bits equal to 1 are added-we print a 0 and we carry a 1.

From the start state we read the first bit. If we read in a 0, we print a 1 and we do not owe a carry bit.

If we read a 1, we print a 0 and we do owe a carry bit.

If at any point in the process we are in no-carry (which means that we do not owe a carry), we print the next bit just as we read it and remain in no-carry.

However, if at some point in the process we are in owe-carry, the situation is different. If we read a 0, we print a 1 and go to the no-carry state.

If we are in owe-carry and we read a 1, we print a 0 and we loop back to owe-carry. The complete picture for this machine is:

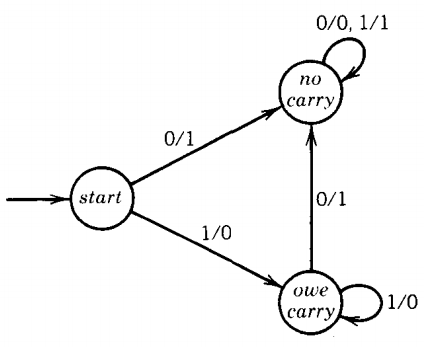
Let us watch this machine in action on the binary representation for the number eleven, 1011. The string is fed into the machine as 1101 (backwards).

The first 1 causes a 0 to be printed and sends us to owe-carry. The next 1 causes a 0 to be printed and loops back to owe-carry.

The next input letter is a 0 and causes a 1 to be printed on our way to no-carry. The next bit, 1, is printed out, as it is fed in, on the no-carry loop.

The total output string is 0011, which when reversed is 1100, and is, as desired, the binary representation for the number twelve.

As simple as this machine is, it can be simplified even further (see Problem 18). This machine has the typical Mealy machine property that the output string is exactly as long as the input string.

This means that if we ran this incrementation machine on the input 1111 we would get 0000. We must interpret the owe-carry state as an overflow situation if a string ever ends there.

There is a connection between Mealy machines and sequential circuits (which we touch on at the end of this chapter) that makes them a very valuable component of Computer Theory.

The two examples we have just presented are also valuable to computing. Once we have an incrementer, we can build a machine that can perform the addition of binary numbers, and then we can use the l's complementing machine to build a subtracting machine based on the following principle:

If a and b are strings of bits, then the subtraction a - b can be performed by (1) adding the l's complement of b to a ignoring any overflow digit and (2) incrementing the results by 1.

For example,

14 - 5 (decimal) = 1110 - 0101 (binary)

- 1110 + l's complement of 0101 + 1 (binary)

= 1110 + 1010 + 1 (binary)

= [1] 1001 binary --> (dropping the [1]) = 9 (decimal)

18 - 7 = 10010 - 00111 --> 10010 + 11000 + 1

= [1]01011 --> 01011 = 11 (decimal)

The same trick works in decimal notation if we use 9's complements, that is, replace each digit d in the second number by the digit (9 - d). For example, 46 - 17 --> 46 + 82 + 1 = [1]29 ---> 29.

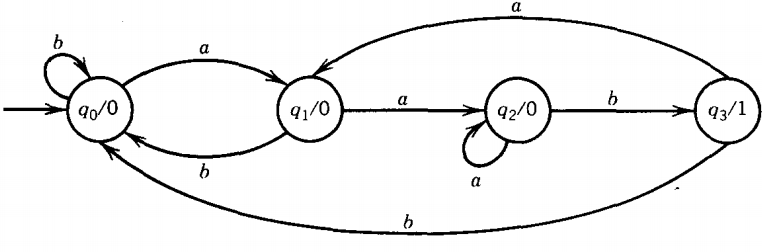
Q. The Mealy machine below will take a string of a's and b's and print out a string of 0's and 1's such that if the nth output character is a 1 it means that the nth input letter is the second in a pair of double letters.

Even though a Mealy machine does not accept or reject an input string, it can recognize a language by making its output string answer some questions about the input.

We have discussed before the language of all words that have a double letter in them.

The Mealy machine below will take a string of a's and b's and print out a string of O's and l's such that if the nth output character is a 1 it means that the nth input letter is the second in a pair of double letters.

For example ababbaab becomes 00001010 with l's in the position of the second of each pair of repeated letters.

This is similar to the Moore machine that recognized the number of occurrences of the substring aab.

This machine recognizes the occurrences of aa or bb. Notice that the triple letter word aaa produces the output 011 since the second and third letters are both the back end of a pair of double a's.

So far, our definition of the equivalence of two machines has been that they accept the same language.

In this sense we cannot compare a Mealy machine and a Moore machine.

However, we may say that two output automata are equivalent if they always give the same output string when presented with the same input string.

In this way, two Mealy machines may be equivalent and two Moore machines may be equivalent, but a Moore machine can never be equivalent to a Mealy machine because the length of the output string from a Moore machine is one longer than that from a Mealy machine given the same input.

The problem is that a Moore machine always begins with one automatic start symbol.

To get around this difficulty, we define a Mealy machine to be equivalent to a Moore machine whenever they always result in the same output if the automatic start symbol for the Moore machine is deleted from the front of the output

Given the Mealy machine Me and the Moore machine Mo, which prints the automatic start-state character x, we will say that these two machines are equivalent if for every input string the output string from Mo is exactly x concatenated with the output from Me.

Rather than debate the merits of the two types of machine, we prove that for every Moore machine there is an equivalent Mealy machine and for every Mealy machine there is an equivalent Moore machine.

We can then say that the two types of machine are completely equivalent.

The proof will be by constructive algorithm. Consider any particular state in Mo-call it q4.

It gives instructions to print a certain character - call it t.

Let us consider all the edges that enter this state.

Each of them is labeled with an input letter.

Let us change this, Let us relabel all the edges coming into q4. If they were previously labeled a or b or c . . . , let them now be labeled a/t or b/t or c/t . . . and let us erase the t from inside the state q4 .

This mean that we shall be printing a t on the incoming edges before they enter q

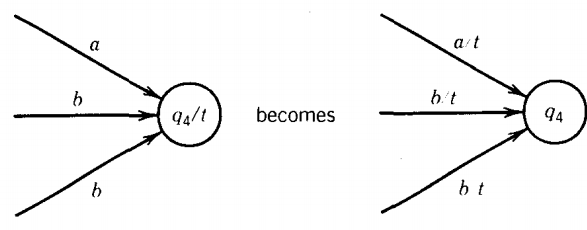
We leave the outgoing edges from q4 alone. They will be relabeled to print the character associated with the state to which they lead.

If we repeat this procedure for every state q0, q1, . . . , we turn Mo into a Mealy machine Me.

As we move from state to state, the things that get printed are exactly what Mo would have printed itself.

The symbol that used to be printed automatically when the machine started in state q0 is no longer the first output character, but this does not stop the rest of the output string from being the same.

Therefore, every Mo is equivalent to some Me.

Q. Below, a Moore machine is converted into a Mealy machine by the algorithm of the proof above.

We cannot just do the reverse of the previous procedure. If we were to try to push the printing instruction from the edge as it is in Me to the inside of the state as it should be for a Moore machine, we might end up with a conflict.

Two edges might come into the same state but have different printing instructions, as in this example.

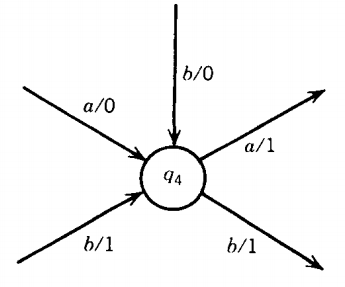
What we need then are twin copies of the same state. The edge a/0 will go into q4¹ (q4 copy 1) and the edge b/1 will go into q4² (q4 copy 2).

The edge labeled b/0 will also go into q4¹.

Inside these states, we include the printing instuctions q4¹/0 and q4¹/1.

The arrows coming out of each of these copies of what used to be q4 must be the same as the edges coming out of q4 originally.

We get two sets of the output edges each equal to the original out-edges but the one set of original in-edges is divided between the two copies.

The example above becomes:

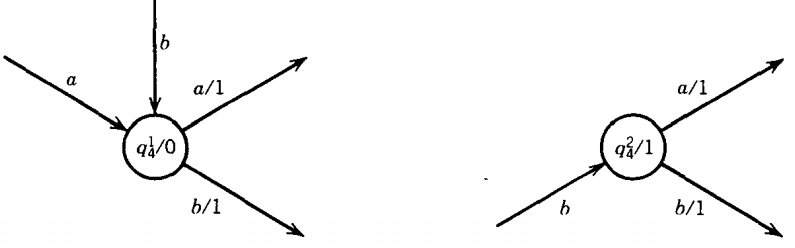
The instruction to print a 0 or a 1 is now found inside the state, not along the edge.

State by state we repeat this procedure. If all the edges coming into the object state have the same printing instruction, then we can simply move that printing instruction into the state.

This does not effect the edges coming out of the state.

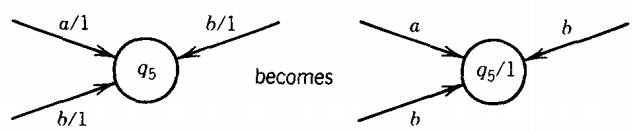
If there is more than one possibility for printing as we enter the state, then we need a copy of the state for each character we might have to print.

(We may need as many copies as there are characters in F.)

All the edges that entered a certain state that used to be labeled something / t

now lead into the copy of that state that instructs us to print the character t.

Each of the copies of the orginal state retains a complete set of the original outgoing edges.

The labels on the incoming edges lose their printing instructions. The letters on the outgoing edges retain them if they have not lost them already.

This algorithm slowly turns a Mealy into a Moore state by state

Examples : Changes in edges and loops

One interesting consequence of this algorithm is that an edge that was a loop in Me may become one edge that is not a loop and one that is a loop in Mo.

For example,

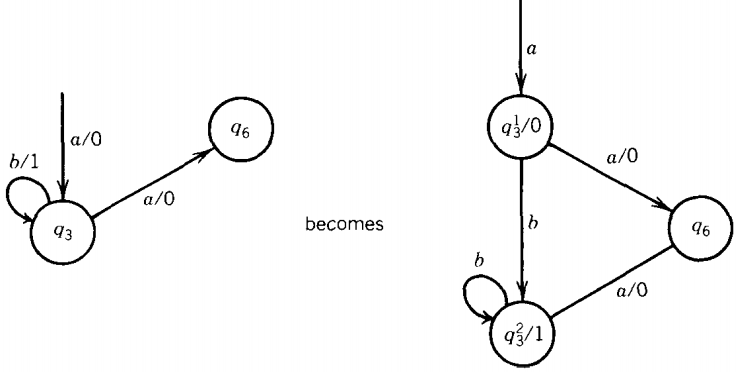
What happens in the example above is that the edge labeled a/0 has to enter a version of q3 that prints a 0.

We call this q3¹/0.

The loop labeled b/1 at q3 has to enter a version of q3 that prints a 1.

We call this q3²/1.

When we enter q3 from the edge a/0, we enter q3¹/0, but we must also be able to loop with b's while staying in a q3-like state.

Therefore, an edge labeled b must connect q3¹/0 to q3²/1.

Since we must be allowed to repeat as many b's as we want there must be a b loop at the state q3²/1. Each b loop we go around prints another 1 when it reenters q3².

As with all such twin descendants, they must both be connected to q6 by a/0.

If there is ever a state that has no edges entering it, we can assign it any printing instruction we want, even if this state is the start state.

Let us repeat this process for each state of Me, q0, q1, . . . . . . This will produce Mo

If we have to make copies of the start state in Me, we can let any one of them be the start state in Mo since they all give the identical directions for proceeding to other states.

Having a choice of start states means that the conversion of Me into Mo is not unique.

We should expect this since any Me is equivalent to more than one Mo.

It is equivalent to the Mo with automatic start symbol 0, or to the Mo with automatic start symbol 1 ....

As we run a string on the Mo that we have produced, we move from state to state very much as in the Me.

It may not be the exact same state that we enter but one of the clones of the original.

But this copy sends us along the same direction that the original did. We end up printing the same sequence of output characters.

The only difference is that when we start up the machine initially we print some unpredictable character, specified by the start state, that does not correspond to any output from Me, because Me never prints before reading an input letter.

But we allowed for this discrepancy in the definition of equivalence, so there is no problem.

Together, Theorems 8 and 9 allow us to say Me = Mo. When we went from Mo to Me, we kept the same number of states and same number of edges. When we go from Me to Mo, these can both increase drastically

Moore machine

Mealy machine

DEFINITION

THEOREM : If Mo is a Moore machine, then there is a Mealy machine Me that is equivalent to it.

THEOREM : For every Mealy machine Me there is a Moore machine Mo that is equivalent to it