NP Completeness
Almost all the algorithms we have studied thus far have been polynomial-time algorithms: on inputs of size n, their worst-case running time is O(nk) for some constant k.
Turing’s famous “Halting Problem,” that cannot be solved by any computer, no matter how much time we allow. There are also problems that can be solved, but not in time O(nk) for any constant k. Generally, we think of problems that are solvable by polynomial-time algorithms as being tractable, or easy, and problems that require super - polynomial time as being intractable, or hard.
No polynomial-time algorithm has yet been discovered for an NP-complete problem, nor has anyone yet been able to prove that no polynomial-time algorithm can exist for any one of them.
Any problem in P is also in NP. So we say P ⊆ NP
| Polynomial Time - Solvable | NP |
|---|---|
| With negative edge weights, finding shortest paths from a single source in a directed graph G(V,E) takes O(VE) time. | Merely determining whether a graph contains a simple path with at least a given number of edges. |
| Determining whether a graph has a euler tour | Determining whether a graph has a hamiltonian tour |
| Problem is solvable in polynomial time | Problem is verifiable in polynomial time |
| Problem is solvable in polynomial time | Problem is verifiable in polynomial time |
| Decision problem is in P class if a deterministic algorithm for its solution runs in polynomial time | Decision problem is in P class if a non deterministic algorithm for its solution runs in polynomial time |
|
|
| Decision problems when converted from non deterministic form to deterministic form then the time complexity increases as in above example from O(1) to O(n). | Non deterministic algorithm has two phases: Guessing phase in which solution is guessed and then Verification phase when the solution which was guessed is verified. |
NP Completeness v/s NP Hard
| NP Complete | NP Hard |
|---|---|
| Decision problems are in this category and the time complexity is low. | Optimization problems whose time complexities are high. |
| We get approximate solution as input is known and problem can be converted into polynomial time solvable problem. | We do not get approximation algorithm as exact input is not known. |
| Ex: Given a graph G = (V,E) and integer 'k' is there a coloring of G using at the most k colors so that no two colors have adjacent vertices having same color. | Ex: Minimum number of colors required to color a graph G = (V,E) so that no two colors have adjacent vertices having same color. i.e. find the chromatic number of the graph. |
| Ex: Given a weighted graph G(V,E) representing the integers k, is there a tour having a cost of 'k' at the most? | Ex: Find the tour of traveling salesperson of minimum cost. |
Traveling Salesperson Problem
Find the shortest tour of a salesperson who has to go cover 50 cities (without repetition) and all cities are connected to each other.
Traveling salesperson is a NP complete problem as if we try to solve such problems for a large input the time taken shall be prohibitive and unacceptable.
Since these optimization are NP hard i.e atleast as hard as the decision problems , their time complexities are also high.
Hence we do not accept to find the exact solution to these problems and settle for the approximate solutions which are found in polynomial time.
Moreover, sometimes exact inputs to these problems are not known and so finding exact solutions is difficult. Many times we solve such problems by using a heuristic or a thumb rule as the approximate solution is acceptable.
The obvious heuristic in TSP would be to visit the nearest city from a city . When we develop an approximate solution to a problem we wish to find a measure of the closeness this approximation has with the exact problem
APPROX_TSP()
{Select a start vertex
while ( all cities have not been visited )
{visit an unvisited city that is closest to the city visited last.
}
return to the starting city
}
Linear Programming Problems - Graphical Method
Rules of Linear Programming Problems
Decision Variables: The decision variables are the variables which will decide the output. They represent the ultimate solution. To solve any problem, we first need to identify the decision variables. The variables are used to formulate the inqualities
Objective Function: It is defined as the objective of making decisions. Profit, Output, Sales, Loss are the objective functions. These have to minimized or maximised
Constraints: The constraints are the restrictions or limitations on the decision variables. They usually limit the value of the decision variables.
Non-negativity restriction: For all linear programs, the decision variables should always take non-negative values. Which means the values for decision variables should be greater than or equal to 0.
Example: A farmer has recently acquired an 110 hectares piece of land. He has decided to grow Wheat and barley on that land. Due to the quality of the sun and the region’s excellent climate, the entire production of Wheat and Barley can be sold. He wants to know how to plant each variety in the 110 hectares, given the costs, net profits and labor requirements according to the data shown below. The farmer has a budget of US$10,000 and an availability of 1,200 man-days during the planning horizon. Find the optimal solution and the optimal value.
| Variety | Cost (Price/Hec) | Net Profit (Price/Hec) | Man-days/Hec |
|---|---|---|---|
| Wheat | 100 | 50 | 10 |
| Barley | 200 | 120 | 30 |
Step 1: Identify the decision variables
The total area for growing Wheat = X (in hectares)
The total area for growing Barley = Y (in hectares)
X and Y are my decision variables.
Step 2: Write the objective function
Since the production from the entire land can be sold in the market. The farmer would want to maximize the profit for his total produce.
We are given net profit for both Wheat and Barley. The farmer earns a net profit of Rs. 50 for each hectare of Wheat and Rs. 120 for each Barley.
Our objective function (given by Z) is, Max Z = 50X + 120Y
Step 3: Writing the constraints
It is given that the farmer has a total budget of Rs. 10,000. The cost of producing Wheat and Barley per hectare is mentioned. We have an upper cap on the total cost spent by the farmer.
Considering above we get 100X + 200Y ≤ 10,000
The next constraint is, the upper cap on the availability on the total number of man-days for planning horizon. The total number of man-days available are 1200. As per the table, we are given the man-days per hectare for Wheat and Barley: 10X + 30Y ≤ 1200
The third constraint is the total area present for plantation. The total available area is 110 hectares. So the equation becomes, X + Y ≤ 110
Step 4: The non-negativity restriction
X ≥ 0, Y ≥ 0
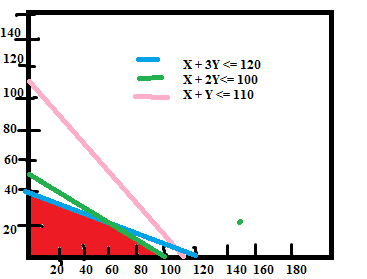
The optimal feasible solution is achieved at the point of intersection where the budget & man-days constraints are active. This means the point at which the equations X + 2Y ≤ 100 and X + 3Y ≤ 120 intersect gives us the optimal solution.
The values for X and Y which gives the optimal solution is at (60,20).
To maximize profit the farmer should produce Wheat and Barley in 60 hectares and 20 hectares of land respectively. The maximum profit the company will gain is,
Max Z = 50 * (60) + 120 * (20) = Rs. 5400
Linear Programming Problems - Simplex Method
Simplex Method to solve Linear Programming
Simplex method consists of three stages.
All equality constraints and unconstrained variables are pivoted.
One uses the simplex pivoting rules to obtain a feasible solution for the problem or its dual.
One improves the feasible solution according to the simplex pivoting rules until the optimal solution is found.
Steps:
Find the objective function.
Find out the constraints.
Convert inequality constraints to equality by adding slack variables. Add one slack variable for each constraint and express constraints in matrix form.
Choose a pivot column of the simplex tableau matrix (column that has the smallest number in the last row). That is column having the smallest number in the last row of the simplex table is called pivot column.
Choose the pivot row for computation (row that has the biggest number in the last column).
Determine the pivot element, the intersection of pivot row and pivot column.
Change the pivot element to 1 by dividing the pivot row by pivot element.
Change the other elements in pivot column to 0 by performing row operations.
If there are no negative numbers left in the last row then stop else go to step 4.
The advertising alternatives for a company include television, newspaper and radio advertisements. The cost for each medium with their audience coverage is given below. The local newspaper limits the number of advertisements from a single company to ten. Moreover, in order to balance the advertising among the three types of media, no more than half of the total number of advertisements should occur on the radio. And at least 10% should occur on television. The weekly advertising budget is Rs. 18,200. How many advertisements should be run in each of the three types of media to maximize the total audience?
| Television | Newspaper | Radio | |
|---|---|---|---|
| Cost per advertisement | 2000 | 600 | 300 |
| Audience per advertisement | 100,000 | 40,000 | 18,000 |
Let X1, X2 and X3 represent the number of advertisements in television, newspaper, and radio, respectively
The objective function is Maximize Z = 100,000X1 + 40,000X2 + 18,000X3
The constraints
2000X1 + 600X2 + 300X3 ≤ 18,200
X2 ≤ 10
X3 ≤ 0.5( X1 + X2 + X3 )
X1 ≥ 0.1( X1 + X2 + X3 )
Simplifying the constraints we get:
20X1 + 6X2 + 3X3 ≤ 182
X2 ≤ 10
- X1 - X2 + X3 ≤ 0
- 9X1 + X2 + X3 ≤ 0
Adding Slack variables to the constraints:
20X1 + 6X2 + 3X3 + S1 =182
X2 + S2 = 10
- X1 - X2 + X3 + S3 = 0
- 9X1 + X2 + X3 + S4 =0
Initial Simplex Table is as shown below:
| X1 | X2 | X3 | S1 | S2 | S3 | S4 | B | |
|---|---|---|---|---|---|---|---|---|
| 20 | 6 | 3 | 1 | 0 | 0 | 0 | 182 (Pivot row) | S1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 10 | S2 |
| -1 | -1 | 1 | 0 | 0 | 1 | 0 | 0 | S3 |
| -9 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | S4 |
| -100000 (PIVOT COLUMN) | -40000 | -18000 | 0 | 0 | 0 | 0 | 0 |
Row operations are: R3 + R1, R4 + 9 * R1, R5 + 100000 R1 :
| X1 | X2 | X3 | S1 | S2 | S3 | S4 | B | |
|---|---|---|---|---|---|---|---|---|
| 1 | 3/10 | 3/20 | 1/20 | 0 | 0 | 0 | 91/10 | X1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 10 (PIVOT ROW) | S2 |
| 0 | -7/10 | 23/20 | 1/20 | 0 | 1 | 0 | 91/10 | S3 |
| 0 | 37/10 | 47/20 | 9/20 | 0 | 0 | 1 | 819/10 | S4 |
| 0 | -10000 (PIVOT COLUMN) | -3000 | 5000 | 0 | 0 | 0 |
Row operations performed are: R1 - 3/10 R2, R3 + 7/10 R2, R4 - 37/10 R2 :
| X1 | X2 | X3 | S1 | S2 | S3 | S4 | B | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3/20 | 1/20 | -3/10 | 0 | 0 | 61/10 | X1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 10 | X2 |
| 0 | 0 | 23/20 | 1/20 | 7/10 | 1 | 0 | 161/10 (PIVOT ROW) | S3 |
| 0 | 0 | 47/20 | 9/20 | -37/10 | 0 | 1 | 449/10 | S4 |
| 0 | 0 | -3000 (PIVOT COLUMN) | 5000 | 10000 | 0 | 0 |
Row operations performed are: R1 - 3/2 R3, R4 - 47/20R3 :
| X1 | X2 | X3 | S1 | S2 | S3 | S4 | B | |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1/23 | -9/23 | -3/23 | 0 | 4 | X1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 10 | X2 |
| 0 | 0 | 1 | 1/23 | 14/23 | 20/23 | 0 | 14 | X3 |
| 0 | 0 | 0 | 8/23 | -118/23 | -47/23 | 1 | 12 | S4 |
| 0 | 0 | 0 | 118k/23 | 272k/23 | 60k/23 | 0 |
The values of the decision variables are:
X1 = 4, X2 = 10, X3 = 14 and Z = 100,000X1 + 40,000X2 + 18,000X3
=100000*4+40000*10+18000*14
=1,052,000 Audience per week
Bayes Probability Theorem
Bayes’ theorem describes the probability of occurrence of an event related to any condition. For example: if we have to calculate the probability of taking a blue ball out of second bag out of three different bags of balls, each bag containing three different color balls viz. red, blue, black. Such case where probability of occurrence of an event is calculated depending on other conditions is known as conditional probability.

Derivation of Bayes’ Theorem:
Statement: Let {\(E_1, E_2,…,E_n\)} be a set of events associated with a sample space \(S\), where all the events \(E_1, E_2,…, E_n\) have nonzero probability of occurrence and they form a partition of \(S\). Let \(A\) be any event associated with \(S\), then according to Bayes’ theorem,
\(P(E_i│A)~=~\frac{P(E_i)P(E_i│A)}{\sum\limits_{k=0}^{n}P(E_k)P(A| E_k)}\)
Proof:According to conditional probability formula,
\(P(E_i│A)~=~\frac{P(E_i ∩ A)}{P(A)}\) ⋯⋯⋯⋯⋯⋯⋯⋯(1)
Using multiplication rule of probability,\(P(E_i ∩ A)~= ~P(E_i)P(E_i│A)\)⋯⋯⋯⋯⋯⋯⋯⋯(2)
Using total probability theorem,\(P(A)~=~\sum\limits_{k=0}^{n}~P(E_k)P(A| E_k)\)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(3)
Putting the values from equations 2 and 3 in equation 1, we get
\(P(E_i│A)~=~\frac{P(E_i)P(E_i│A)}{\sum\limits_{k=0}^n~P(E_k)P(A| E_k)}\)
Bayes Probability Theorem - Examples
Example 1: Bag I contains 4 white and 6 black balls while another Bag II contains 4 white and 3 black balls. One ball is drawn at random from one of the bags and it is found to be black. Find the probability that it was drawn from Bag I.
Solution: Let \(E_1\) be the event of choosing the bag I, \(E_2\) the event of choosing the bag II and A be the event of drawing a black ball.
Then, \(P(E_1)~ = ~P(E_2)~ =~\frac{1}{2}\)
Also, \(P(A|E_1) ~= ~P\)(drawing a black ball from Bag I) = \(\frac{6}{10}~ = ~\frac{3}{5}\)
\(P(A|E_2) ~=~ P\)(drawing a black ball from Bag II) = \(\frac{3}{7}\)
By using Bayes’ theorem, the probability of drawing a black ball from bag I out of two bags,
\(P(E_1 |A)~ =~\frac{P(E_1)P(A|E_1)}{P(E_1 )P(A│E_1 )+ P(E_2)P(A|E_2)}\)
=\(\frac{\frac{1}{2}~\times~\frac{3}{5}}{\frac{1}{2}~\times~\frac{3}{7}~+~\frac{1}{2}~ ×~\frac{3}{5}}\) = \(\frac{7}{12}\)
Example 2: A man is known to speak truth 2 out of 3 times. He throws a die and reports that number obtained is a four. Find the probability that the number obtained is actually a four.
Solution:Let \(A\) be the event that the man reports that number four is obtained.
Let \(E_1\) be the event that four is obtained and \(E_2\) be its complementary event.
Then, \(P(E_1)\) = Probability that four occurs = \(\frac{1}{6}\)
\(P(E_2)\) = Probability that four does not occurs = \(1 ~–~ P(E_1) ~=~ 1~-\frac{1}{6}~ =~\frac{5}{6}\)
Also, \(P(A|E_1)\) = Probability that man reports four and it is actually a four = \(\frac{2}{3}\)
\(P(A|E_2)\) = Probability that man reports four and it is not a four = \(\frac{1}{3}\)
By using Bayes’ theorem, probability that number obtained is actually a four,
\(P(E_1 |A)~ =~ \frac{P(E_1)P(A|E_1)}{P(E_1 )P(A│E_1 )~+~ P(E_2)P(A|E_2)}~
=~\frac{\frac{1}{6} ~ ×~ \frac{2}{3}}{\frac{1}{6} ~×~ \frac{2}{3}~ +~ \frac{5}{6}~ ×~\frac{1}{3}}\) = \(\frac{2}{7}\)
Solved Question Papers
Q.6Consider the following Code(Gate 2015 Set1)
int fun1 (int n)
{
int i, j, k, p, q = 0;
for (i = 1; i<n; ++i)
{
p = 0;
for (j=n; j>1; j=j/2)
++p;
for (k=1; k<p; k=k*2)
++q;
}
return q;
}
n3
n(logn)2
nlogn
nlog(logn)
Ans (D)
int fun1 (int n)
{
int i, j, k, p, q = 0;
// This loop runs (n) time
for (i = 1; i < n; ++i)
{
p = 0;
// This loop runs (Log n) times. for (j=n; j > 1; j=j/2)
++p;
// Since above loop runs (Log n) times, p = (Log n)
// This loop runs (Log p) times which loglogn
for (k=1; k <p; k=k*2)
++q;
}
return q;
}
Q. Which of the given options provides the increasing order of asymptotic
complexity of functions f1,f2,f3 and f4?
f1(n)=2n; f2(n)=n3/2; f3(n)=n log2 n; f4(n)=nlog2 n
(GATE 2011)
f3, f2, f4,f1
f3, f2, f1,f4
f2, f3, f1,f4
f2, f3, f4,f1
Ans . 1
Let n=1024
f1(n)=21024
f2(n)=215
f3(n)=10 x 210
f4(n)=102410=2100
Therefore, f3 , f2 , f4 , f1 is the required increasing order
Q. Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n>0) return (n%r) + foo (n / r, r );
else return 0;
}
What is the return value of the function foo when it is called as foo (513, 2)?
(GATE 2011)
9
8
5
2
Ans . 4
Q. Consider the following recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n>0) return (n%r) + foo (n / r, r );
else return 0;
}
What is the return value of the function foo when it is called as foo (345, 10) ?
(GATE 2011)
345
12
5
3
Ans . 2
Q. Consider the following C function (GATE 2017 Paper 2)
int fun (int n)
{
int i, j ;
for (i = 1; i <= n; i++)
{
for (j = 1; j < n; j += i)
{
printf("%d %d"; i, j) ;
}
}
}
Time complexity of fun in terms of Θ notation is
-
\(\ominus\left(n\sqrt{n}\right)\)
-
\(\ominus\left(n^{2}\right)\)
-
\(\ominus\left(n\log{n}\right)\)
-
\(\ominus\left(n^{2}\log{n}\right)\)
Ans. 3
for i = 1 ⇒ j will run from 1 to n by incrementing by '1' in each step ⇒ j will run for n times
for i = 2 ⇒ j will run from 1 to n by incrementing by '2' in each step ⇒ j will run for n = 2 times and so on
Time Complexity
\(= n + n/2 + n/3 + ... + n/n\)
\(= n\left(1+1/2+1/3+..1/n\right)\)
\(= \ominus\left(n\log{n}\right)\)
Q. A message is made up entirely of characters from the set X= P,Q,R,S,T. The table of probabilities for each of the characters is shown below: (GATE 2017 Paper 2)
| Character | Probability |
|---|---|
| P | 0.22 |
| Q | 0.34 |
| R | 0.17 |
| S | 0.19 |
| T | 0.08 |
| Total | 0.22 |
If a message of 100 characters over X is encoded using Huffman coding, then the expected length of the encoded message in bits is
Ans. 225
Huffman tree is as follows :
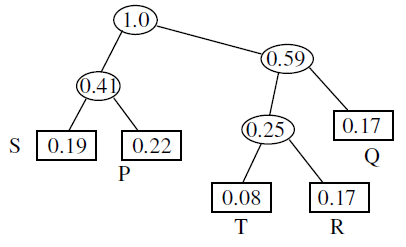
Average length of the character
\(=2\left(0.19+0.22\right)+2\left(0.34\right)+3\left(0.08+0.17\right)\)
\(=2\left(0.41\right)+2\left(0.34\right)+3\left(0.25\right)\)
\(=0.82 + 0.68 + 0.75\)
\(= 2.25\) bits
Message length \(= 100 * 2.25\) bits \(= 225\) bits
Q. What is the return value of f(p,p) if the value of p is initialized to 5 before the call? Note that the first parameter is passed by reference, whereas the second parameter is passed by value. \(int \ f(int \ \& x, int \ c) \{ \) \(c = c-1; \) \(if(c == 0) \) \(return \ 1; \) \(x = x + 1; \) \(return \ f(x,c)*x; \) \(\}\) (GATE 2013 SET D)
3024
6561
55440
161051
Ans . 2
Since, Reference of p is passed as ’x’. Thus, Any changes in value of x in f would be reflected globally. The recursion can be broken as :
\( f \begin{bmatrix}5 & 5 \\x & c \end{bmatrix} \rightarrow x \times f \begin{bmatrix}6 & 4 \\x& c \end{bmatrix} \rightarrow x \times f \begin{bmatrix}7 & 3 \\x& c \end{bmatrix} \rightarrow x \times f \begin{bmatrix}8 & 2 \\x& c \end{bmatrix} \rightarrow x \times f \begin{bmatrix}9 & 1 \\x& c \end{bmatrix} \rightarrow 9 \)
Our Answer = \( x\times x \times x \times x ... where x = 9 \)
\(9^{4} = 6561 \)
Q. A certain computation generates two arrays a and b such that a[i] = f(i) for 0 = i < n and b[i] = g(a[i]) for 0 = i < n. Suppose this computation is decomposed into two concurrent processes X and Y such that X computes the array a and Y computes the array b. The processes employ two binary semaphores R and S, both initialized to zero. The array a is shared by the two processes. The structures of the processes are shown below. Process X: private i; for(i = 0;i < n;i + +){ a[i] = f(i); ExitX(R,S); } Process Y: private i; for(i = 0;i < n;i + +){ EntryY (R,S); b[i] = g(a[i]); } Which one of the following represents the CORRECT implementations of ExitX and EntryY? (GATE 2013 SET D)
ExitX(R, S) { P(R); V(S); } EntryY(R,S){ P(S); V(R); }
ExitX(R, S) { V(R); V(S); } EntryY(R,S){ P(R); P(S); }
ExitX(R, S) { P(S); V(R); } EntryY(R,S){ V(S); P(R); }
ExitX(R, S) { V(R); P(S); } EntryY(R,S){ V(S); P(R); }
Ans . 3
For computing both the array a[] and b[], first element a[i] should be computed using which b[i] can be computed. So process X and Y should run in strict alteration manner, starting with X. This requirement meets with implementation of ExitX and EntryY given in option C.
Q. Consider the following function \( int \ unknown (int n) \{ \) \(int \ i, j, k = 0; \) \( for(i=n/2; i <= n; i++)\){ \( for(j=2; j <= n; j=j*2) \){ \(k=k+n/2; \) \(return (k);\) \(\}\) The return value of the function is ? (GATE 2013 SET D)
\(\theta(n^2)\)
\(\theta(n^2\log n)\)
\(\theta(n^3) \)
\(\theta(n^3\log n) \)
Ans . 2
The outer for loop goes for \(\frac{n}{2} + 1\) iterations. The inner for loop runs independent of the outer loop. And for each inner iteration. \(\frac{n}{2} \) gets added to k.
\(outer\_answer = \frac{n}{2} \times outer\_loops \times inner\_loops\_per\_outer\_loop \)
\( inner\_loops = \theta(\log n)\)
\(2^{\theta (n\log n)} = \theta(n)\)
\(answer = \frac{n}{2} + [ \frac{n}{2} +1] \times \theta(\log n) =\theta(n^{2} \log n)\)
\(L_1 = \left\{O^{p} 1^{q} O^{r} \mid p, q, r \geq 0 \right\} \)
\(L_2 = \left\{O^{p} 1^{q} O^{r} \mid p, q, r \geq 0, p\neq r \right\} \)
Q.6 unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
} (GATE 2011)
345
12
5
3
Ans . (B)
The call foo(345, 10) returns sum of decimal digits (because r is 10) in the number n. Sum of digits for 345 is 3 + 4 + 5 = 12.

Q.7 Consider the same recursive C function that takes two arguments
unsigned int foo(unsigned int n, unsigned int r) {
if (n > 0) return (n%r + foo (n/r, r ));
else return 0;
}
What is the return value of the function foo when it is called as foo(513, 2)?
(GATE 2011)
9
8
5
2
Ans . (D)
foo(513, 2) will return 1 + foo(256, 2). All subsequent recursive calls (including foo(256, 2)) will return 0 + foo(n/2, 2) except the last call foo(1, 2) .
The last call foo(1, 2) returns 1. So, the value returned by foo(513, 2) is 1 + 0 + 0…. + 0 + 1.
The function foo(n, 2) basically returns sum of bits (or count of set bits) in the numb.
Q. Consider the following C program(GATE Paper-2008)
int f1(int n)
{
if(n == 0 || n == 1)
return n;
else
return (2*f1(n-1) + 3*f1(n-2));
}
int f2(int n)
{
int i;
int X[N], Y[N], Z[N] ;
X[0] = Y[0] = Z[0] = 0;
X[1] = 1; Y[1] = 2; Z[1] = 3;
for(i = 2; i <= n; i++)
{
X[i] = Y[i-1] + Z[i-2];
Y[i] = 2*X[i];
Z[i] = 3*X[i];
}
return X[n] ;
}
The running time of f1(n) and f2(n) are
θ(n) and θ(n)
θ(2^n) and θ(n)
θ(n) and θ(2^n)
θ(2^n) and θ(2^n)
Ans . (2)
Explanation :
For f1(), let T(n) be the function for time complexity.
T(n) = T(n-1) + T(n-2)
Above recursion is a standard one for Fibonacci Numbers. After solving the recursion, we get
T(n) = 1/sqrt(5)[(1 + sqrt(5))/2]^n - 1/sqrt(5)[(1 - sqrt(5))/2]^n Above recursion can also be written as Θ(1.618.^n)
In f2(), there is a single loop, so time complexity is Θ(n)
Consider the program given in above question, f1(8) and f2(8) return the values
1661 and 1640
59 and 59
1640 and 1640
1640 and 1661
Ans . (3)
Explaination :
Both functions perform same operation, so output is same, means either (B) or (C) is correct.
f1(2) = 2*f1(1) + 3*f1(0) = 2
f1(3) = 2*f1(2) + 3*f1(1) = 2*2 + 3*1 = 7
f1(4) = 2*f1(3) + 3*f1(2) = 2*7 + 3*2 = 20
f1(5) = 2*f1(4) + 3*f1(3) = 2*20 + 3*7 = 40 + 21 = 61
We can skip after this as the only remaining choice is (C)
f1(6) = 2*f1(5) + 3*f1(4) = 2*61 + 3*20 = 122 + 60 = 182
f1(7) = 2*f1(6) + 3*f1(5) = 2*182 + 3*61 = 364 + 183 = 547
f1(8) = 2*f1(7) + 3*f1(6) = 2*547 + 3*182 = 1094 + 546 = 1640
Q.1 Assuming P != NP, which of the following is true ? (GATE 2012 )
(A) NP-complete = NP
(B) NP-complete \cap P = \Phi
(C) NP-hard = NP
(D) P = NP-complete
Ans . B
An NP-Complete problem cannot be solved in polynomial time.
Because, if one NP-Complete problem can be solved in polynomial time, then all NP problems can be solved in polynomial time.
If that is the case, then NP and P set become same, which is not true.
Q.Which graph is planar? (GATE 2012)
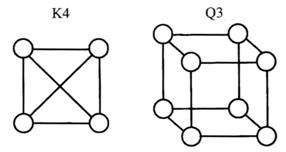
(A) K4 is planar while Q3 is not
(B) Both K4 and Q3 are planar
(C) Q3 is planar while K4 is not
(D) Neither K4 nor Q3 are planar
Answer: (B)
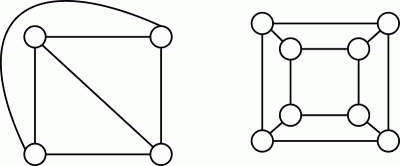
Explanation: A Graph is said to be planar if it can be drawn in a plane without any edges crossing each other.
Following are planar embedding of the given two graphs
Diagram
Q. A max-heap is a heap where the value of each parent is greater than or equal to the values of its children. Which of the following is a max-heap?
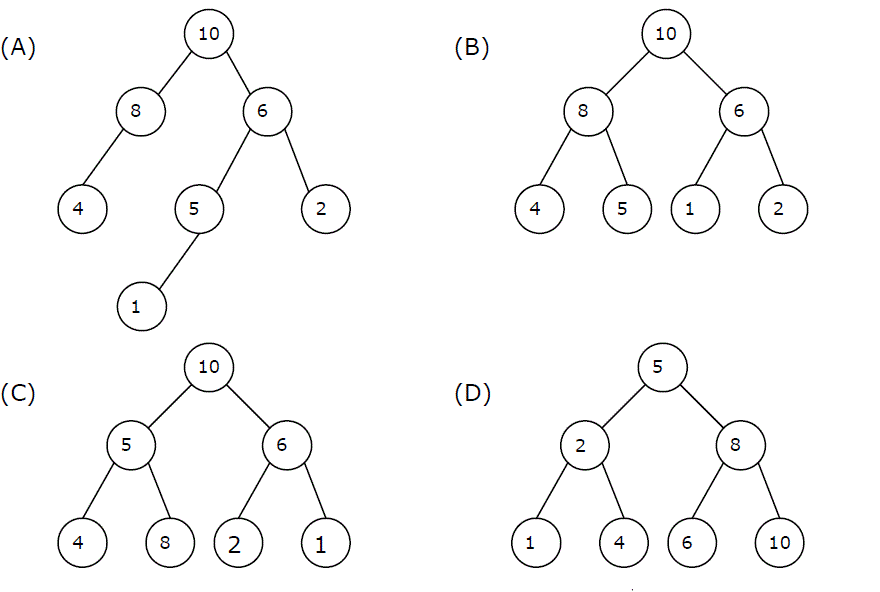
Ans .
Answer: (B)
A binary tree is max-heap if it is a complete binary tree (A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible) and it follows the max-heap property (value of each parent is greater than or equal to the values of its children).
- A) is not a max-heap because it is not a complete binary tree
- B) is a max-heap because it is complete binary tree and follows max-heap property.
- C) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property.
- D) is not a max-heap because 8 is a chile of 5 in this tree, so violates the max-heap property. There are many other nodes in this tree which violate max-heap property in this tree.
Q. Consider the following C function (GATE 2007)
Int f(int n)
{
static int r=0;
if (n<= 0) return 1;
if (n > 3)
{
r = n;
return f(n-2) +2;
}
return f(n-1) +r;
}
What is the value of f(5)?
-
5
-
7
-
9
-
18
Ans. 4
f(5) sets up r an 5, and then calls f(3) and contributes an addition of 2. f(3) calls f(2), f(1), f(0) each contributing 5 to the sum. Finally f(1) returns contributing 1 to the total. Total is 1 + 5 + 5 +5 +2 = 18.
Q. Consider the following C code segment: (GATE 2007)
Int IsPrime(n)
{
int I, n;
for ( I = 2; I <= sqrt(n); I ++)
if(n % I == 0 )
{printf(“Not Prime/n”); return 0;}
return I ;
}
Let T\left(n\right) denote the number of times the for loop is executed by the program on input n. Which of the following is TRUE?
-
\(T\left(n\right)=o\left(\sqrt{n}\right) and T\left(n\right)=\omega\left(\sqrt{n}\right)\)
-
\(T\left(n\right)=o\left(\sqrt{n}\right) and T\left(n\right)=\omega\left(1\right)\)
-
\(T\left(n\right)=o\left(n\right) and T\left(n\right)=\omega\left(\sqrt{n}\right)\)
-
None of the above.
Ans. 1
Note that sqrt(n) does not change in the iteration. So we have a simple for statement which has an index variable varying from 2 to vn)
Q. Let w be the minimum weight among all the edge weights in an undirected connected graph. Let e be a specific edge of weight w. Which of the following is FALSE? (GATE 2007)
-
There is a minimum spanning tree containing e.
-
If e is not in a minimum spanning tree T, then in the cycle formed by adding e to T, all edges have the same weight.
-
Every minimum spanning tree has an edge of weight w.
-
e is present in every minimum spanning tree.
Ans. 4
If all the edges in a complete graph have the same weight there are many minimum spanning trees and a particular edge may not necessarily be in all the trees. A is true as we start by including an edge of minimum weight for an instance of the minimum spanning tree. The minimum weight edge has to be in the minimum spanning tree so C is true. If e is excluded, then all the other edges must be of the same weight.
Q. Consider the following program (GATE 2001)
Program P2
var n: int:
procedure W(var x: int)
begin
x=x+1;
print x;
end
procedure D
begin
var n: int;
n=3;
W(n);
end
begin //beginP2
n=10;
D;
end
If the language has dynamic scoping and parameters are passed by reference, what will be printed by the program?
-
10
-
11
-
3
-
None of the above
Ans. 4
Explanation:
In static scoping or compile-time scoping the free variables (variables used in a function that are neither local variables nor parameters of that function) are referred as global variables because at compile only global variables are available.
In dynamic scoping or run-time scoping the free variables are referred as the variables in the most recent frame of function call stack. In the given code in the function call of procedure W the local variable x is printed i.e 4. Under dynamic scoping if x would have not been there in procedure W then we would refer to x of the function in function call stack i.e procedure D and the main function but since x is a local variable not a free variable we referred to the local variable hence 4 will be printed.
Q. Which of the below three functions are likely to cause problems with pointers? (GATE 2001)
[PI] int * g (void)
{
int x= 10;
return (&x);
}
[P2] int * g (void)
{
int * px;
*px= 10;
return px;
}
[P3] int * g (void)
{
int *px;
px = (int *) malloc (sizeof(int));
*px= 10;
return px;
}
-
Only P3
-
Only P1 and P3
-
Only P1 and P2
-
P1, P2 and P3
Ans. 3
Q. What is printed by the print statements in the program P1 assuming call by reference parameter passing? (GATE 2001)
Program P1()
{
x = 10;
y = 3;
func1(y,x,x);
print x;
print y;
}
func1(x,y,z)
{
y = y+4;
z = x+y+z;
}
-
10,3
- 31,3
- 27,7
- None of the above
Explanation:
Here, we are passing the variables by call by reference. This means that the changes that we will make in the parameter would be reflected in the passed argument.
Here, the first variable passed in the function func1 (i.e., y) points to the address of the variable x.
Similarly, the second variable passed in the function func1 (i.e., x) points to the address of the variable y and the third variable passed in the function func1 (i.e., x) points to the address of the variable z
So, we have y = y + 4 ? y = 10 + 4 = 14
and z = x + y + z ? z = 14 + 14 + 3 = 31
z will be returned to x. So, x = 31 and y will remain 3.
Thus, the correct choice is B.