Context-free grammars come in a wide variety of forms. By definition, any finite string of terminals and nonterminals is a legal right-hand side of a production, for example, X → YaaYbaYXZabYb

Any context-free language in which Λ is a word must have some Λ-productions in its grammar since otherwise we could never derive the word Λ from S.

This statement is obvious, but it should be given some justification. Λ-productions are the only productions that shorten the working string.

If we begin with the string S and apply only non-Λ-productions, we never develop a word of length 0.

However, there are some grammars that generate languages that do not include the word Λ but that contain some Λ-productions anyway.

One such CFG that we have already encountered is

S → aX X → Λ

for the single word a. There are other CFG's that generate this same language that do not include any Λ-productions.

If L is a context-free language generated by a CFG that includes Λ-productions, then there is a different context-free grammar that has no Λ-productions that generates either the whole language L (if L does not include the word Λ) or else generates the language of all the words in L that are not Λ.

PROOF :

We prove this by providing a constructive algorithm that will convert a CFG that contains Λ-productions into a CFG that does not contain Λ-productions that generates the same language with the possible exception of the word Λ.

Consider the purpose of the production N → Λ

If we apply this production to some working string, say abAbNaB, we get abAbaB.

In other words, the net result is to delete N from the working string. If N was just destined to be deleted, why did we let it get there in the first place ?

Its mere presence in the working string cannot have affected the nonterminals around it since productions are applied to one symbol at a time no matter what its neighbors are.

This is why we call these grammars context free. A nonterminal in a working string in a derivation is not a catalyst; it is not there to make other changes possible.

It is only there so that eventually it will be replaced by one of several possibilities.

It represents a decision we have yet to make, a fork in the road, a branching node in a tree.

If N is simply destined to be removed we need a means of avoiding putting that N into the string at all. This is not quite so simple as it sounds.

Consider the following CFG for EVEN PALINDROME (the language of all palindromes with an even number of letters):

S → aSa | bSb | Λ

In this grammar we have the following possible derivation:

S ⇒ aSa
⇒ aaSaa
⇒ aabSbaa
⇒ aabbaa

We obviously need the nonterminal S in the production process even though we delete it from the derivation when it has served its purpose.

The following rule seems to take care of using and deleting the nonterminals involved in Λ-productions.

If, in a certain CFG, there is a production of the form N → Λ among the set of productions, where N is any nonterminal (even S), then we can modify the grammar by deleting this production and adding the following list of productions in its place.

For all productions of the form: X → (blah 1) N (blah 2)

where X is any nonterminal (even S or N) and where (blah 1) and (blah 2) are anything at all (even involving N), add the production X → (blah 1) (blah 2)

Notice, we do not delete the production X → (blah 1) N (blah 2), only the production N → Λ.

For all productions that involve more than one N on the right side add new productions that have the other characters the same but that have all possible subsets of N's deleted.

For example, the production
X → aNbNa
makes us add
X → abNa (deleting only the first N)
X → aNba (deleting only the second N)
and
X → aba (deleting both N's)
Also,
X → NN
makes us add
X → N (deleting one N)
and
X → Λ (deleting both N's)

Instead of using a production with an N and then dropping the N later we simply use the correct form of the production with the N already dropped.

There is then no need to remove N later and so no need for the lambda production.

This modification of the CFG will produce a new CFG that generates exactly the same words as the first grammar with the possible exception of the word Λ. This is the end of the Proposed Replacement Rule.

We remove the production S → Λ and replace it with S → aa and S → bb, which are the first two productions with the right-side S deleted.

The CFG is now: S → aSa | bSb | aa | bb

which also generates EVENPALINDROME, except for the word A, which can no longer be derived.

The reason this rule works is that if the N was put into the working string by the production

X → (blah 1) N (blah 2)
and later deleted by
N → Λ

both steps could have been done at once by using the replacement production X → (blah 1) (blah 2)

in the first place. We have seen that, in general, a change in the order in which we apply the productions may change the word generated. However, in this case, no matter how far apart the productions

X → (blah 1) N (blah 2)
and
N → Λ

may be in the sequence of the derivation, if the N removed from the working string by the second production is the same N introduced by the first then these two can be combined into the single production

X → (blah 1) (blah 2)

We must be careful not to remove N before it has served its full purpose. For example, the following EVENPALINDROME derivation is generated in the old CFG:

Derivation Production Used

S ⇒ aSa S → aSa

⇒ aaSaa S → aSa

⇒ aabSbaa S → bSb

⇒ aabbaa S → Λ

In the new CFG we can combine the last two steps into one:

Derivation Production Used

S ⇒ aSa S → aSa

⇒ aaSaa S → aSa

⇒ aabSbaa S → bb

It is only the last two steps for which we use the replacement production:

We do not eliminate the entire possibility of using S to form words. We can now use this proposed replacement rule to describe an algorithm for eliminating all Λ-productions from a given grammar.

If a particular CFG has several nonterminals with Λ-productions, then we replace these Λ-productions one by one following the steps of the proposed replacement rule.

As we saw, we will get more productions (new right sides by deleting some N's) but shorter derivations (by combining the steps that formerly employed Λ-productions).

We end up with a CFG that generates the exact same language as the original CFG (with the possible exception of the word Λ) but that has no Λ-productions.

A little discussion is in order here to establish that the new CFG actually does generate all the non-Λ words the old CFG does and that it generates no new words that the old CFG did not.

In the general case we might have something like this. In a long derivation in a grammar that includes the productions B → aN and N → Λ among other stuff we might find:

S ⇒ ....
S ⇒ a A N b B a
⇒ a A N b a N a from B → aN
...
⇒ abbXybaNa
⇒ aabbXybaa from N → Λ

Notice that not all the N's have to turn into Λ's. The first N in the working string did not, but the second does. We trace back to the step at which this second N was originally incorporated into the working string.

In this sketchy example, it came from the production B → aN. In the new CFG we would have a corresponding production B → a. If we had applied this production

instead of B → aN, there would be no need later to apply N → Λ to this particular N. Those never born need never die.

(First statistician: "With all the troubles in this world, it would be better if we were never born in the first place." Second statistician: "Yes, but how many are so lucky? Maybe one in ten thousand.")

So we see that we can produce all the old non-Λ words with the new CFG even without Λ-productions.

To show that the new CFG with its new productions does not generate any new words that the old CFG could not, we merely observe that each of the new added productions is just a combination of old productions 'and any new derivation corresponds to some old derivation that used the Λ-production.

Before we claim that this constructive algorithm provides the whole proof, we must ask if it is finite.

It seems that if we start with some nonterminals N₁, N₂, N₃, which have Λ-productions and we eliminate these Λ-productions one by one until there are none left, nothing can go wrong. Can it?

What can go wrong is that the proposed replacement rule may create new Λ-productions that can not themselves be removed without again creating more

For example, in this grammar

S → a | Xb | aYa
X → Y | Λ
Y → b | X
we have the Λ-production
X → Λ

so by the replacement rule we can eliminate this production and put in its place the additional productions:

S → b (from S → Xb)
and
Y → Λ (from Y → X)

But now we have created a new Λ-production which was not there before.

So we still have the same number of Λ-productions we started with. If we now use the proposed replacement rule to get rid of Y → Λ, we get

S → aa (from S → aYa)
and
X → Λ (from X → Y)

But we have now re-created the production X → Λ. So we are back with our old Λ-production.

In this particular case the proposed replacement rule will never eliminate all Λ-productions even in hundreds of applications.

In a given CFG, we call a nonterminal N nullable if

1. There is a production N → Λ
or
2. There is a derivation that starts at N and leads to Λ
N ⇒ .. ⇒ Λ

Modified Replacement Rule

Delete all A-productions.

Add the following productions: For every production X → old string

add enough new productions of the form X → . . . . that the right side will account for any modification of the old string that can be formed by deleting all possible subsets of nullable nonterminals, except that we do not allow X → Λ to be formed even if all the characters in this old right-side string are nullable.

Q. For example, in the CFG
S → a | Xb | aYa
X → Y | Λ
Y → b | X

We find that X and Y are nullable. So when we delete X → Λ we have to check all productions that include X or Y to see what new productions to add:

Old Productions with Nullables Productions Newly Formed by the Rule

X → Y Nothing

X → Λ Nothing

Y → X Nothing

S → Xb S → b

S → aYa S → aa

The new CFG is :
S → a | Xb | aYa | b | aa
X → Y
Y → b | X

It has no A-productions but generates the same language.

This modified replacement rule works the way we thought the first replacement rule would work, that is, by looking ahead at which nonterminals in the working string will be eliminated by A-productions and offering alternate substitutions in which they have already been eliminated.

Example

S → Xay | YY | aX | ZYX
X → Za | bZ | ZZ | Yb
Y → Ya | XY | Λ
Z → aX | YYY

all the nonterminals are nullable, as we can see from S ⇒ ZYX ⇒ YYYYX ⇒ YYYYZZ ⇒ YYYYYYYZ ⇒ YYYYYYYYYY
⇒ ... ⇒ ΛΛΛΛΛΛΛΛΛΛ = Λ

Let us start by painting all the nonterminals with A-productions blue. We paint every occurrence of them, throughout the entire CFG, blue. Now for Step 2 we paint blue all nonterminals that produce solid blue strings. For example, if

S → ZYX

and Z, Y, and X are all blue, then we paint S blue. Paint all other occurrences of S throughout the CFG blue too.

As with the FA's, we repeat Step 2 until nothing new is painted. At this point all nullable nonterminals will be blue.

This is an effective decision procedure to determine all nullables, and therefore the modified replacement rule is also effective.

This then successfully concludes the proof of this Theorem.

Q. Let us consider the following CFG for the language defined by (a + b)*a
S → Xa
X → aX | bX | Λ

The only nullable nonterminal here is X, and the productions that have right sides including X are:

Old Productions with Nullables Productions Newly Formed by the Rule

S → Xa S → a

X → aX X → a

X → bX X → b

The full new CFG is:
S → Xa | a
X → aX | bX | a | b

To produce the word baa we formerly used the derivation:

Derivation Production Used

S ⇒ Xa S → Xa

⇒ bXa X → bX

⇒ baXa X → aX

⇒ baa X → Λ

Now we combine the last two steps, and the new derivation in the new CFG is:

S ⇒ Xa        S → Xa
⇒ bXa        X → bX
⇒ baa        X → a

Since Λ was not a word generated by the old CFG, the new CFG generates exactly the same language.

Q. Consider this inefficient CFG for the language defined by

(a + b)*bb(a + b)*
S → XY
X → Zb
Y → bW
Z → AB
W → Z
A → aA | bA | Λ
B → Ba | Bb | Λ

From X we can derive any word ending in b; from Y we can derive any word starting with b. Therefore, from S we can derive any word with a double b.

Obviously, A and B are nullable. Based on that, Z - AB makes Z also nullable. After that, we see that W is also nullable. X, Y, and S remain nonnullable. Alternately, of course, we could have arrived at this by azure artistry.

The modified replacement algorithm tells us to generate new productions to replace the Λ-productions as follows:

Old	Additional New Productions Derived from Old
X → Zb	X → b
Y → bW	Y → b
Z → AB	Z → A and Z → B
W → Z	Nothing
A → aA	A → a
A → bA	A → b
B → Ba	B → a
B → Bb	B → b

Remember we do not eliminate all of the old productions, only the old A-productions.

The fully modified new CFG is:

S → XY
X → Zb | b
Y → bW | b
Z → AB | A | B
W → Z
A → aA | bA | a | b
B → Ba | Bb | a | b

Since Λ was not a word generated by the old CFG, the new CFG generates exactly the same language.

A production of the form : one Nonterminal → one Nonterminal is called a unit production.

THEOREM : If there is a CFG for the language L that has no Λ-productions, then there is also a CFG for L with no Λ-productions and no unit productions.

PROOF :

This will be another proof by constructive algorithm. First we ask ourselves what is the purpose of a production of the form

A → B
where A and B are nonterminals.

We can use it only to change some working string of the form

(blah) A (blah)
into the working string
(blah) B (blah)

why would we want to do that? We do it because later we want to apply a production to the nonterminal B that is different from any that we could produce from A. For example,

B → (string)
so
(blah) A (blab) ⇒ (blah) B (blah) ⇒ (blab) (string) (blah)

which is a change we could not make without using A → B, since we had no production A → (string).

It seems simple then to say that instead of unit productions all we need are more choices for replacements for A.

We now formulate a replacement rule for, eliminating unit productions.

Elimination Rule

For every pair of nonterminals A and B, if the CFG has a unit production A → B or if there is a chain of unit productions leading from A to B, such as A ⇒ X1 ⇒ X2 ⇒ .. ⇒ B

where X1, X2 are some nonterminals, we then introduce new productions according to the following rule: If the nonunit productions from B are B → s₁ | s₂ | s₃ | ....

where s₁, s₂ and s₃ are strings, create the productions: A → s₁ | s₂ | s₃ | ....

We do the same for all such pairs of A's and B's simultaneously. We can then eliminate all unit productions.

This is what we meant to do originally. If in the derivation for some word w the nonterminal A is in the working string and it gets replaced by a unit production A → B, or by a sequence of unit productions leading to B, and further if B is replaced by the production B → s₄ , we can accomplish the same thing and derive the same word w by employing the production A → s₄ directly in the first place.

This modified elimination rule avoids circularity by removing all unit productions at once. If the grammar contains no Λ-productions, it is not a hard task to find all sequences of unit productions A → S₁ → S₂ → ... → B, since there are only finitely many unit productions and they chain up in only obvious ways.

In a grammar with Λ-productions, and nullable nonterminals X and Y, the production S → ZYX is essentially a unit production.

There are no Λ - productions allowed by the hypothesis of the theorem so no such difficulty is possible.

The modified method described in the proof is an effective procedure and it proves the theorem.

Example

Let us reconsider the example mentioned in the proof above
S → A | bb
A → B | b
B → S | a

Let us separate the units from the nonunits:

Unit Productions Decent Folks

S ⇒ A S → bb

A ⇒ B A → b

B ⇒ S B → a

We list all unit productions and sequences of unit productions, one nonterminal at a time, tracing each nonterminal through each sequence it heads.

Then we create the new productions that allow the first nonterminal to be replaced by any of the strings that could replace the last nonterminal in the sequence.

S → A gives S → b
S → A → B gives S → a
A → B gives A → a
A → B → S gives A → bb
B → S gives B → bb
B → S → A gives B → b

The new CFG for this language is:

S → bb | b | a
A → b | a | bb
B → a | bb | b

which has no unit productions.

Parenthetically, we may remark that this particular CFG generates a finite language since there are no nonterminals in any string produced from S.

THEOREM

If L is a language generated by some CFG, then there is another CFG that generates all the non-Λ words of L, all of whose productions are of one of two basic forms:

Nonterminal → string of only Nonterminals
or
Nonterminal → one terminal

Example :

Let us start with the CFG:

S → X₁ | X₂aX₂ | aSb | b
X₁ → X₂X₂ | b
X₂ → aX₂ | aaX₁

After the conversion we have:

S → X₁         X₁ → X₂X₂
S → X₂AX₂         X₁ → B
S → ASB         X₂ → AX₂
S → B         X₂ → AAX₁
A → a
B → b

We have not employed the disjunction slash | but instead have written out all the productions separately so that we may observe eight of the form:

Nonterminal → string of Nonterminals
and two of the form:
Nonterminal → one terminal

In all cases where the algorithm of the theorem is applied the new CFG has the same number of terminals as the old CFG and more nonterminals (one new one for each terminal).

As with all our proofs by constructive algorithm, we have not said that this new CFG is the best example of a CFG that fits the desired format.

We say only that it is one of those that satisfy the requirements.

One problem is that we may create unit productions where none existed before. For example, if we follow the algorithm to the letter of the law,

X → a
will become
X → A
A → a

To avoid this problem, we should add a clause to our algorithm saying that any productions that we find that are already in one of the desired forms, should be left alone: "If it ain't broke, don't fix it." Then we do not run the risk of creating unit productions (or Λ-productions for that matter).

S → Na
N → a | b

S → NN
N → a | b

The answer is that bb is not generated by the first grammar but it is by the second. The correct modified form is

S → NA
N → a | b
A → a

The CFG
S → XY
X → XX
Y → YY
X → a
Y → b

(which generates aa*bb*) and which is already in the desired format would, if we mindlessly attacked it with our algorithm, become:

S → XY
X → XX
Y → YY
X → A
Y → B
A → a
B → b

which is also in the desired format but has unit productions.

The goal was to prove the existence of an equivalent grammar in the specified format.

The virtue here is to find the shortest, most understandable and most elegant proof, not an algorithm with dozens of messy clauses and exceptions.

For any context-free language L the non-Λ words of L can be generated by a grammar in which all productions are of one of two forms:

Nonterminal → string of exactly two Nonterminals

Nonterminal → one terminal

If a CFG has only productions of the form
Nonterminal → string of two Nonterminals
or of the form
Nonterminal → one terminal
it is said to be in Chomsky Normal Form, CNF

Any context-free language that does not contain Λ as a word has a CFG in CNF that generates exactly it. However, if a CFL contains Λ, then when its CFG is converted by the algorithms above into CNF the word Λ drops out of the language while all other words stay the same.

EXAMPLE

Let us convert S → aSa | bSb | a | b | aa | bb. (which generates the language PALINDROME except for Λ) into CNF. This language is called NON NULL PALINDROME.

First we separate the terminals from the nonterminal :
S → ASA
S → BSB
S → AA
S → BB
S → a
S → b
A → a
B → b

Notice that we are careful not to introduce the needless unit productions S--A and S--->B. Now we introduce the R's:

S → AR₁        S → AA
R₁ → SA        S → BB
S → BR₂        S → a
R₂ → SB        S → b
                   A → a
                   B → b

This is in CNF, but it is quite a mess. Had we not seen how it was constructed we would have some difficulty recognizing this grammar as a CFG for NON NULL PALINDROME.

If we include with this list of productions the additional production S → Λ, we have a CFG for the entire language PALINDROME.

EXAMPLE

Let us convert the CFG
S → bA | aB
A → bAA | aS | a
B → aBB | bS | b

into CNF. Since we use the symbols A and B in this grammar already, let us call the new nonterminals we need to incorporate to achieve the form of CNF, X (for a) and Y (for b).

The grammar becomes:

Grammar

S → YA B → XBB

S → XB B → YS

A → YAA B → b

A → XS X → a

A → a Y → b

Notice that we have left well enough alone in two instances:

A → a and B → b

We need to simplify only two productions:

A → YAA becomes A → YR₁ ; R₁ → AA
and
B → XBB becomes B → XR₂ ; R₂ → BB

The CFG has now become:

S → YA | XB
A → YR | XS| a
B → XR₂ | YS | b
X → a
Y → b
R₁ → AA
R₂ → BB

which is in CNF. This is one of the more obscure grammars for the language EQUAL.

Consider the CFG : S → aaaaS | aaaa

which generates the language a⁴ⁿ for n = 1 2 3.... = {a⁴ , a⁸, a¹² ... }

We convert this to CNF as follows:

S → AAAAS
S → AAAA
A → a

which in turn becomes
S → AR₁
R₁ → AR₂
R₂ → AR₃
R₃ → AS
S → AR₄
R₄ → AR₅
R₅ → AA
A → a

The leftmost nonterminal in a working string is the first nonterminal that we encounter when we scan the string from left to right.

EXAMPLE : In the string abNbaXYa, the leftmost nonterminal is N.

DEFINITION

If a word w is generated by a CFG by a certain derivation and at each step in the derivation a rule of production is applied to the leftmost nonterminal in the working string, then this derivation is called a leftmost derivation.

EXAMPLE :

Consider the CFG:
S → aSX | b
X → Xb | a

The following is a leftmost derivation:
S ⇒ aSX
⇒ aaSXX
⇒ aabXX
⇒ aabXbX
⇒ aababX
⇒ aababa

At every stage in the derivation the nonterminal replaced is the leftmost one.

Consider the CFG:

S → XY
X → XX | a
Y → YY | b

We can generate the word aaabb through several different derivations, each of which follows one of these two possible derivation trees:

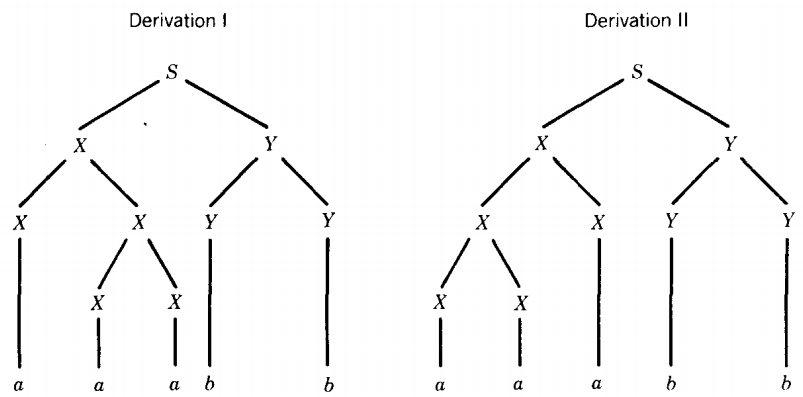
Each of these trees becomes a leftmost derivation when we specify in what order the steps are to be taken.

If we draw a dotted line similar to the one that traces the Polish notation for us, we see that it indicates the order of productions in the leftmost derivation.

We number the nonterminals in the order in which we first meet them on the dotted line. This is the order in which they must be replaced in a leftmost derivation.

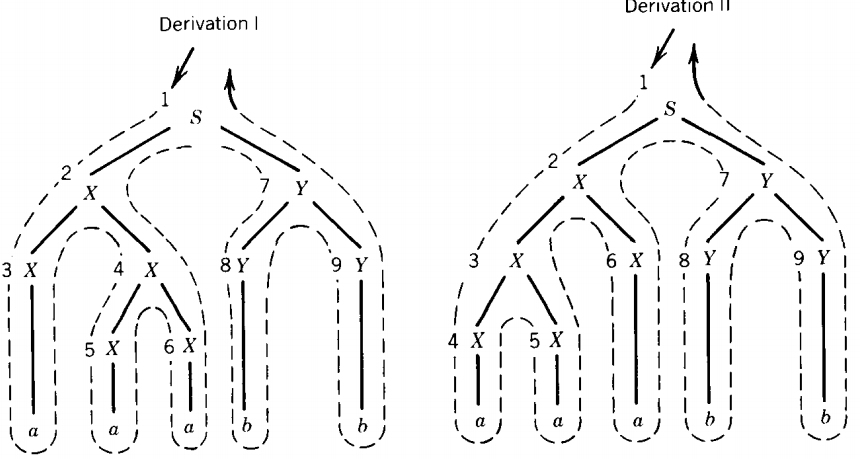
Derivation I	Derivation II
S ⇒ XY	S ⇒ XY
⇒ XXY	⇒ XXY
⇒ aXY	⇒ XXXY
⇒ aXXY	⇒ aXXY
⇒ aaXY	⇒ aaXY
⇒ aaaY	⇒ aaaY
⇒ aaaYY	⇒ aaaYY
⇒ aaabY	⇒ aaabY
⇒ aaabb	⇒ aaabb

In each of these derivations we have drawn a dot over the head of the leftmost nonterminal. It is the one that must be replaced in the next step if we are to have a leftmost derivation.

Any word that can be generated by a given CFG by some derivation also has a leftmost derivation.

EXAMPLE :

Consider the CFG:

S → S ⊃ S | ~S | (S) | p | q

To generate the symbolic logic formula ( p &sups; ( ~p ⊃ q ) )

we use the following tree:

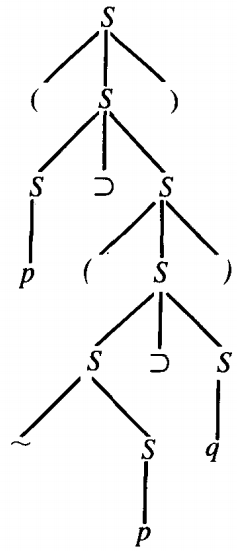
Remember that the terminal symbols are () ⊃ ~ p q

and the only nonterminal is S. We must always replace the left-most S.

S → (S)
→ (S ⊃ S)
→ (p ⊃ S)
→ (p ⊃ (S))
→ ( p ⊃ ( S ⊃ S ) )
→ ( p ⊃ ( ~ S ⊃ S ) )
→ ( p ⊃ ( ~ p ⊃ S ) )
→ ( p ⊃ ( ~ p ⊃ q ) )

CHOMSKY NORMAL FORM

THEOREM

Proposed Replacement Rule

Apply this replacement rule to the following CFG : S → aSa | bSb | Λ

Example

DEFINITION

EXAMPLE

THEOREM

EXAMPLE

DEFINITION

EXAMPLE

THEOREM

Derivation	Production Used
S ⇒ aSa	S → aSa
⇒ aaSaa	S → aSa
⇒ aabSbaa	S → bSb
⇒ aabbaa	S → Λ

Old Productions with Nullables	Productions Newly Formed by the Rule
X → Y	Nothing
X → Λ	Nothing
Y → X	Nothing
S → Xb	S → b
S → aYa	S → aa

Derivation	Production Used
S ⇒ Xa	S → Xa
⇒ bXa	X → bX
⇒ baXa	X → aX
⇒ baa	X → Λ

Grammar
S → YA	B → XBB
S → XB	B → YS
A → YAA	B → b
A → XS	X → a
A → a	Y → b