Given a language L generated by a particular CFG, there is a PDA that accepts exactly L. Given a language L that is accepted by a certain PDA, there exists a CFG that generates exactly L.

Before we describe the algorithm that associates a PDA with a given CFG in its most general form, we shall illustrate it on one particular example.

Let us consider the folowing CFG in CNF

S → SB
S → AB
A → CC
B → b
C → a

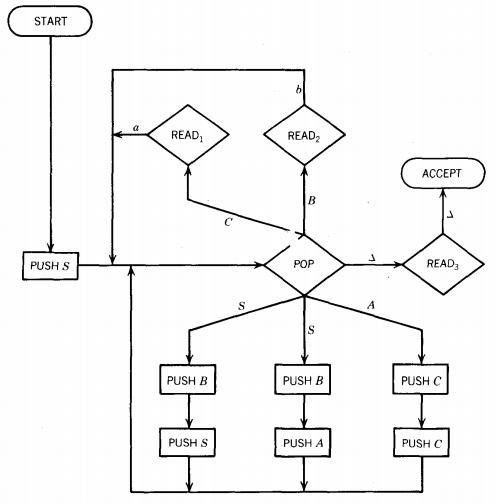
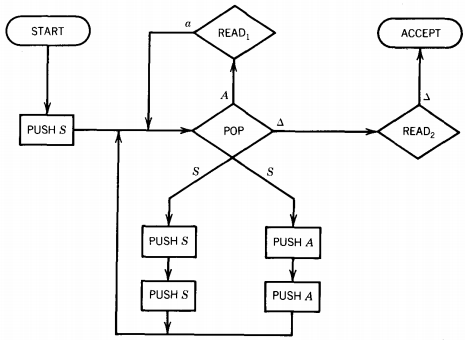
We now propose the nondeterministic PDA pictured below. In this machine the STACK alphabet is

Γ = {S, A, B, C}

Σ = {a, b}

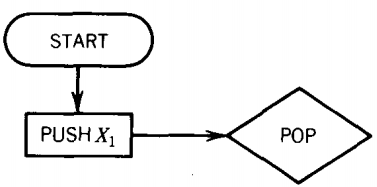
We begin by pushing the symbol S onto the top of the STACK. We then enter the busiest state of this PDA, the central POP.

In this state we read the top character of the STACK.

The STACK will always contain nonterminals exclusively.

Two things are possible when we pop the top of the STACK.

Either we replace the removed nonterminal with two other nonterminals, thereby simulating a production (these are the edges pointing downward) or else we do not replace the nonterminal at all but instead we go to a READ state, which insists we read a specific terminal from the TAPE or else it crashes (these edges point upward).

To get to ACCEPT we must have encountered READ states that wanted to read exactly those letters that were originally on the INPUT TAPE in their exact order.

We now show that to do this means we have simulated a left-most derivation of the input string in this CFG.

The word aab can be generated by leftmost derivation in this grammar as follows:

In CNF all working strings in left-most derivations have the form:

(string of terminals) (string of Nonterminals)

To run this word on this PDA we must follow the same sequence of productions, keeping the STACK contents at all times the same as the string of nonterminals in the working string of the derivation.

We begin at START with

Immediately we push the symbol S onto the STACK

We then head into the central POP. The first production we must simulate is S → AB. We pop the S and then we PUSH B, PUSH A arriving at this:

Note that the contents of the STACK is the same as the string of nonterminals in the working string of the derivation after Step 1.

We again feed back into the central POP. The production we must now simulate is a A → CC. This is done by popping the A and following the path PUSH C, PUSH C.

The situation is now:

Notice that here again the contents of the STACK is the same as the string of nonterminals in the working string of the derivation after Step 2.

Again we feed back into the central POP. This time we must simulate the production C → a. We do this by popping the C and then reading the a from the TAPE. This leaves:

We do not keep any terminals in the STACK, only the nonterminal part of the working string.

Again the STACK contains the string of nonterminals in Step 3 of the derivation.

However, the terminal that would have appeared in front of these in the working string has been cancelled from the front of the TAPE.

Instead of keeping the terminals in the STACK, we erase them from the INPUT TAPE to ensure a perfect match.

The next production we must simulate is another C → a. Again we POP C and READ a. This leaves:

Here again we can see that the contents of the STACK is the string of nonterminals in the working string in Step 4 of the derivation.

The whole working string is aaB, the terminal part aa corresponds to what has been struck from the TAPE.

This time when we enter the central POP we simulate the last production in the derivation, B → b. We pop the B and read the b. This leaves:

This △ represents the fact that there are no nonterminals left in the working string after Step 5. This, of course, means that the generation of the word is complete.

We now reenter the POP, and we must make sure that both STACK and TAPE are empty

POP △ → READ₃ → ACCEPT

The general principle is clear. To accept a word we must follow its leftmost derivation from the CFG. If the word is

ababbbaab

and at some point in its left-most Chomsky derivation we have the working string : a b a b b Z W V

then at this point in the corresponding PDA-processing the status of the STACK and TAPE should be

the used-up part of the TAPE being the string of terminals and the contents of the STACK being the string of nonterminals of the working string. This process continues until we have derived the entire word. We then have

At this point we POP △, go to READ₃, and ACCEPT. There is noticeable nondeterminism in this machine at the POP state.

This parallels, reflects, and simulates the nondeterminism present in the process of generating a word.

In a left-most derivation if we are to replace the nonterminal N we have one possibility for each production that has N as the left side.

Similarly in this PDA we have one path leaving POP for each of these possible productions.

Just as the one set of productions must generate any word in the language, the one machine must have a path to accept any legal word once it sits on the INPUT TAPE.

The point is that the choices of which lines to take out of the central POP tell us how to generate the word through leftmost derivation, since each branch represents a production.

It should also be clear that any input string that reaches ACCEPT has got there by having each of its letters read by simulating Chomsky productions of the form:

Nonterminal → terminal

This means that we have necessarily formed a complete left-most derivation of this word through CFG productions with no terminals left over in the STACK.

Therefore, every word accepted by this PDA is in the language of the CFG.

By the same technique as used before, we produce the following PDA:

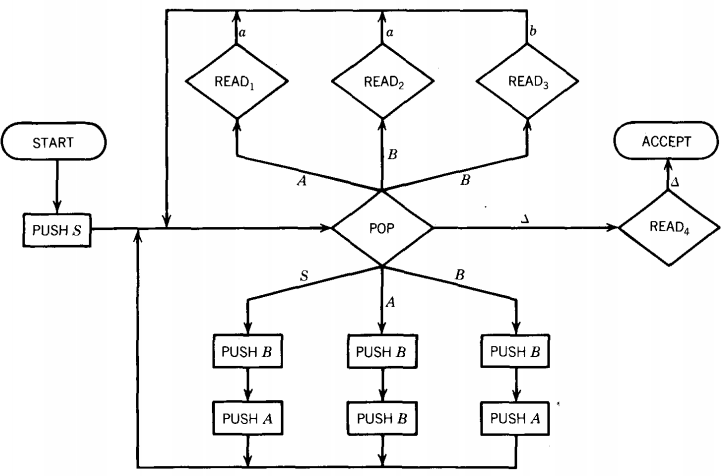
We shall trace simultaneously how the word baaab can be generated by this CFG and how it can be accepted by this PDA.

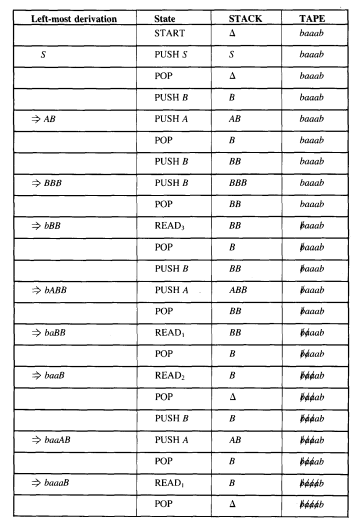
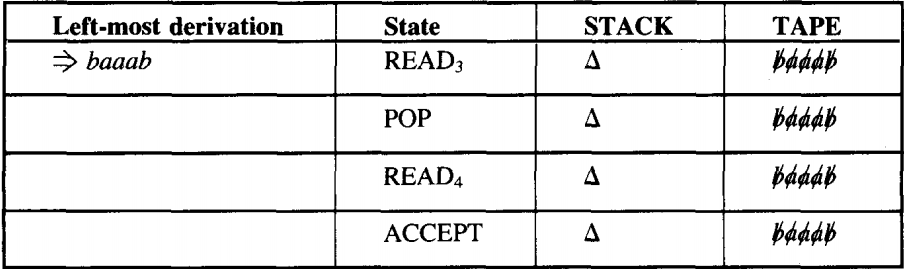
At every stage we have the following equivalence: working string = (letters cancelled from TAPE) (string of nonterminals from STACK)

At the beginning this means:

working string = S
letters cancelled = none
string of nonterminals in STACK = S

At the end this means:

working string = the whole word
letters cancelled = all
STACK = △

Now that we understand this example, we can give the rules for the general case.

If we are given a CFG in CNF as follows:

X₁ → X₂X₃
X₁ → X₃X₄
X₂ → X₂X₂
. . .
X₃ → a
X₄ → a
X₅ → b
. . .

where the start symbol S = X₁, and the other nonterminals are X₂, X₃, we build the following machine:

Begin with

For each production of the form: X_i → X_jX_k

we include this circuit from the POP back to itself:

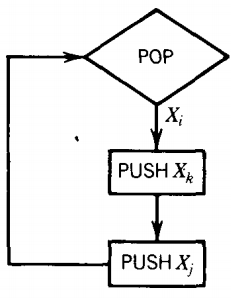
For all productions of the form X_i → b we include this circuit:

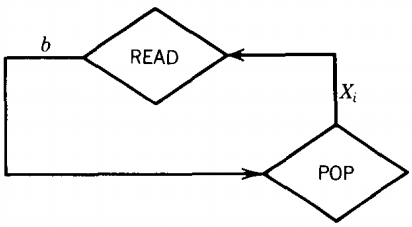
When the stack is finally empty, which means we have converted our last nonterminal to a terminal and the terminals have matched the INPUT TAPE, we follow this path:

From the reasons and examples given above, we know that all words generated by the CFG will be accepted by this machine and all words accepted will have left-most derivations in the CFG.

This does not quite finish the proof. We began by assuming that the CFG was in CNF, but there are some context-free languages that cannot be put into CNF.

They are the languages that include the word Λ. In this case, we can convert all productions into one of the two forms acceptable to CNF while the word Λ must still be included.

To include this word, we need to add another circuit to the PDA, a simple loop at the POP

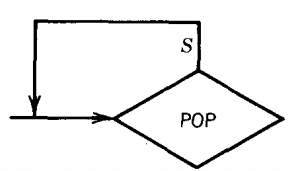
This kills the nonterminal S without replacing it with anything and the next time we enter the POP we get a blank and proceed to accept the word.

The language PALINDROME (including Λ) can be generated by the following CFG in CNF (plus one Λ-production)

The PDA that the algorithm instructs us to build is:

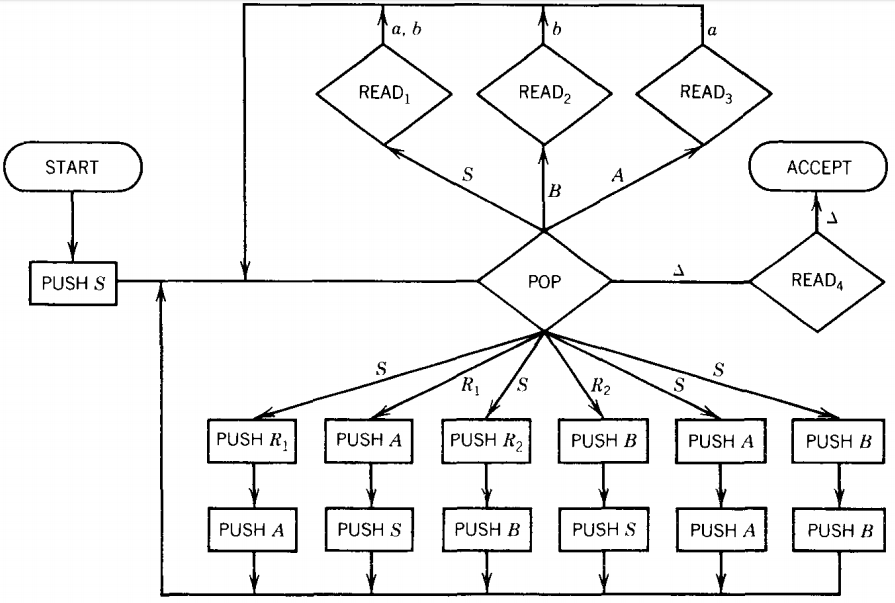
Let us examine how the input string abaaba is accepted by this PDA

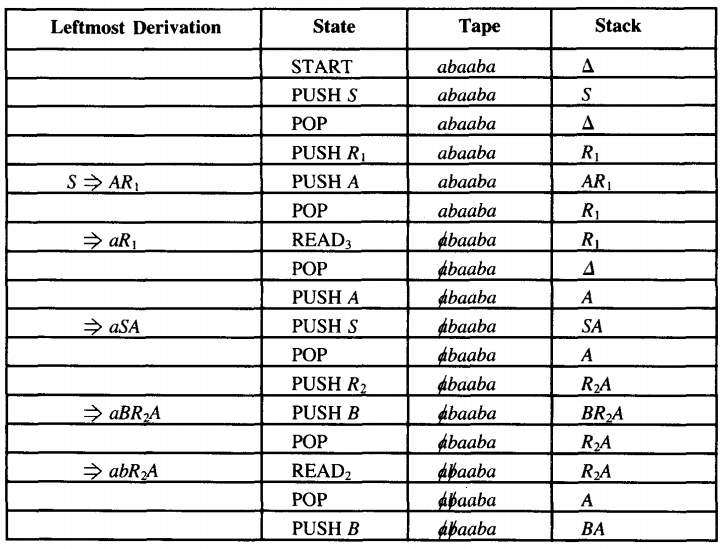
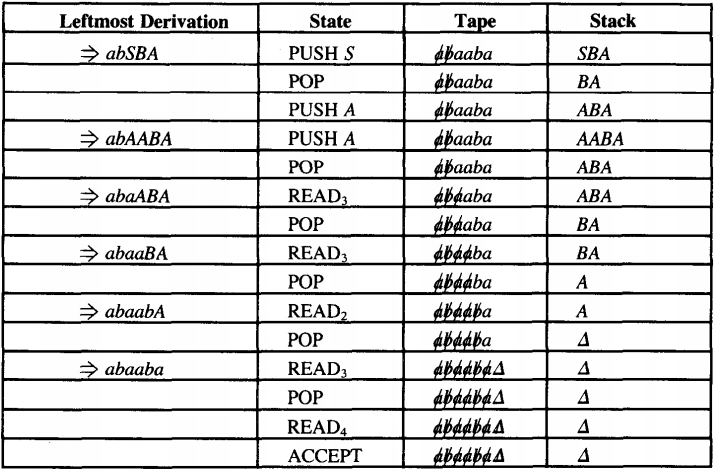
Notice how different this is from the PDA's we developed earlier for the languages EVENPALINDROME and ODDPALINDROME.

We shall now illustrate the complete process of equivalence, as given by the two theorems in this chapter, on one simple example.

We shall start with a CFG and convert it into a PDA, and we then convert this very PDA back into a CFG.

The language of this illustration is the collection of all strings of an even number of a's:

EVENA = (aa)⁺ = a²ⁿ = {aa aaaa aaaaaa ... }

One obvious grammar for this language is : S → SS | aa

The left-most total language tree begins:

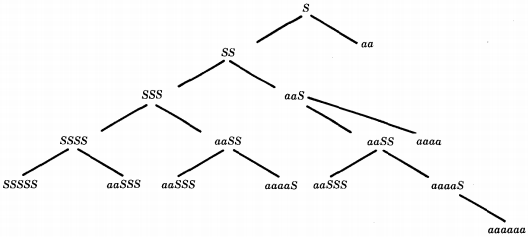
Before we can use the algorithm of conversion to build a PDA that accepts this language, we must put it into CNF. Therefore

S → SS | AA

A → a

The PDA we produce by the conversion algorithm is:

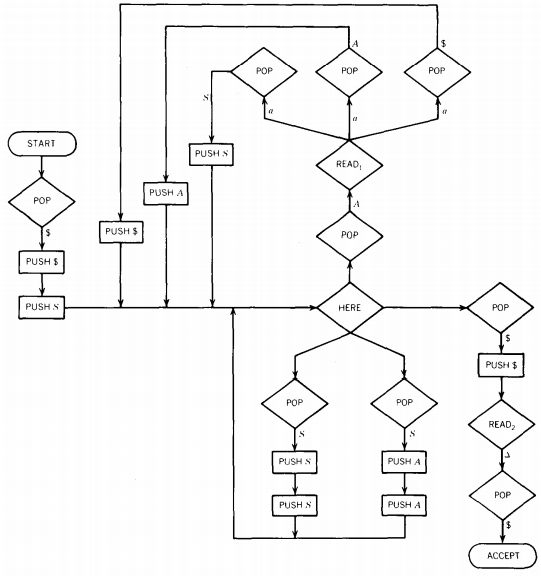
We shall now use the conversion algorithm to turn this machine back into a CFG. First we must put this PDA into conversion form:

Notice that the branching that used to take place at the grand central POP must now take place at the grand central HERE.

Notice also that since we insist there be a POP after every READ, we must have three POP's following READ₁.

The next step is to put this PDA into a summary table:

We are now ready to write out all the productions in the row-language.

We always begin with the production from Rule 1:
S → Net(START,ACCEPT,$)

There are two rows with no PUSH parts and they give us, by Rule 2:
Net(HERE,READ₁ ,A) → Row 4
Net(READ₂ ,ACCEPT,$) → Row9

From Row, we get 12 productions of the form:
Net(START,X, $) → Row₁Net(HERE, Y,$)Net(Y,X, $)
where X = HERE, READ₁, READ₂ , or ACCEPT and Y = HERE, READ₁ or READ₂ .

From Row₂ we get eight productions of the form:
Net(HERE,X,S) → Row₂ Net(HERE,Y,S) Net(Y,X,S)
where X = HERE, READ₁ , READ₂ , or ACCEPT and Y = HERE or READ₁ .

From Row₃ we get eight productions of the form:
Net(HERE,X,S) → Row₃ Net(HERE,Y,A )Net(Y,X,A)
where X = HERE, READ₁ , READ₂ , or ACCEPT and Y = HERE or READ₁ .

From Row₅ we get the four productions:
Net(READ₁,X,S) → Row ₅Net(HERE,X,S)

where X = HERE, READ₁, READ₂, or ACCEPT.

From Row₆ we get the four productions:

From Row₈ we get the one production:

All together, this makes a grammar of 44 productions for the row-language. We shall now do something we have not discussed before.

We can trim from the row-language grammar all the productions that are never used in the derivation of words. For example, in the simple grammar

S → a | X | Ya
X → XX

it is clear that only the production S → a is ever used in the derivation of words in the language. The productions S → X, S → Ya and X → XX, as well as the nonterminals X and Y, are all useless.

Applying algorithm for pruning grammars as follows :

Our question is: In a derivation from S to a string of the terminals, Row₁ , Row₂, . . . , Row₈, which productions can obviously never be used?

If we are ever to turn a working string into a string of solid terminals, we need to use some productions at the end of the derivation that do not introduce nonterminals into the string. In this grammar only two productions are of the form:

Nonterminal → string of terminals

They are:
Net(HERE,READ₁ ,A) → Row4
and
Net(READ₂,ACCEPT,$) → Row9

If any words are generated by this row-language grammar at all, then one of these productions must be employed as the last step in the derivation.

In the step before the last, we should have a working string that contains all terminals except for one of the possible nonterminals Net(HERE,READ₁ ,A) or Net(READ₂ ,ACCEPT,$).

Still counting backward from the final string, we ask: What production could have been used before these two productions to give us such a working string? It must be a production in which the right side contains all terminals and one or both of the nonterminals above.

Of the 44 productions, there are only two that fit this description:

Net(HERE,ACCEPT,$) - Row₈ Net(READ₂ , ACCEPT,$)
Net(READ₁,READ₁,A) - Row₇ Net(HERE,READ₁ ,A)

This gives us two more useful nonterminals, Net(HERE,ACCEPT,$) and Net(READ₁,READ₁,A).

We have now established that any working string containing terminals and some of the four nonterminals:

Net(HERE,READ₁, A)
Net(READ₂ ,ACCEPT,$)
Net(HERE, ACCEPT,$)
Net(READ₁,READ₁,A)

can be turned by these productions into a string of all terminals. Again we ask the question: What could have introduced these nonterminals into the working string?

There are only two productions with right sides that have only terminals and these four nonterminals. They are:

Net(HERE,READ₁,S) → Row₃Net(HERE,READ₁,A )Net(READ₁, READ₁ ,A)
and
Net(READ₁,ACCEPT,$) - Row₆Net(HERE,ACCEPT,$)

We shall call these two nonterminals "useful" as we did before. We can now safely say that any working string that contains terminals and these six nonterminals can be turned into a word.

Again we ask the question: How can these new useful nonterminals show up in a word? The answer is that there are only two productions with right sides that involve only nonterminals known to be useful. They are:

Net(READ₁ ,READ₁,S) → Row₅ Net(HERE,READ₁,S)
and
Net(START,ACCEPT,S) → Row₁Net(HERE,READ₁,S)Net(READ₁,ACCEPT,$)

So now we can include Net(READ₁,READ₁,S) and Net(START,ACCEPT,$) on our list of useful symbols because we know that any working string that contains them and the other useful symbols can be turned by the productions into a word of all terminals.

This technique should be familiar by now. From here we can almost smell the blue paint.

Again we ask which of the remaining productions have useful right sides, that is, which produce strings of only useful symbols? Searching through the list we find two more. They are:

Net(HERE,READ₁,S) → Row₂Net(HERE,READ₁,S)Net(READ₁,READ₁,S)
and
S → Net(START,ACCEPT,$)

This makes both Net(HERE,READ₁,S) and S useful.

This is valuable information since we know that any working string working composed only of useful symbols can be turned into a string of all terminals.

When applied to the working string of just the letter S, we can conclude that there is some language that can be generated from the start symbol.

The row-language therefore contains some words.

When we now go back through the list of 44 productions looking for any others that have right sides composed exclusively of useful symbols we find no new productions.

In other words, each of the other remaining productions introduces onto its right-side some nonterminal that cannot lead to a word.

Therefore, the only useful part of this grammar lies within the 10 productions we have just considered above. Let us recapitulate them:

We can now make an observation from looking at the grammar that could have been made by looking at the PDA alone.

For this particular machine and grammar, each row appears in only one production.

The CFG above is the grammar for the row-language.

To obtain the grammar for the actual language of the PDA, we must also include the following productions:

This grammar is too long and has too many nonterminals for us simply to look at it and tell immediately what language it generates.

So we must perform a few obvious operations to simplify it.

We have been very careful never to claim that we have rules that will enable us to understand the language of a CFG.

First, let us observe that if N is a nonterminal that appears on the left side of productions all of which are of the form: N → string of terminals

then we can eliminate N from the CFG entirely by substituting these rightside strings for N wherever N occurs in the productions (and of course dropping the productions from N).

This simplification will not change the language generated by the CFG.

This trick applies to the CFG before us in many places. For example, the production : Row₆ → a

is of this form and this is the only production from this nonterminal. We can therefore replace the nonterminal Row₆ throughout the grammar with the letter a.

Not only that, but the production Row₂ → Λ

is also of the form specified in the trick. Therefore, we can use it to eliminate the nonterminal Row₂ from the grammar. In fact, all the nonterminals of the form Row_i can be so eliminated.

PROD 1 is a unit production, so we can use the algorithm for eliminating unit productions to combine it with PROD 2. The result is:

S → Net(HERE,READ₁,S)Net(READ₁,ACCEPT,$)

,As we said before any nonterminal N that has only one production: N → some string can be eliminated from the grammar by substituting the right-side string for N everywhere it appears.

As we shall presently show this rule can be used to eliminate all the nonterminals in the present CFG except for the symbol S and Net(HERE,READ₁,S), which is the left side of two different productions.

We shall illustrate this process in separate stages. First, we obtain:

Notice that the READ₂'s completely disappear. We can now combine PROD 9 and 10 with PROD 7. PROD 8 and 5 can be combined with PROD 4 and 5. Also PROD 6 can be combined with PROD 1 and 2 to give:

S → Net(HERE,READ₁,S)a

Now let us rename the nonterminal Net(HERE,READ₁,S) calling it X. The entire grammar has been reduced to

S → Xa
X → XaX
X → a

This CFG generates the same language as the PDA. However, it is not identical to the CFG with which we started. To see that this CFG does generate EVENA, we draw the beginning of its left-most total language tree.

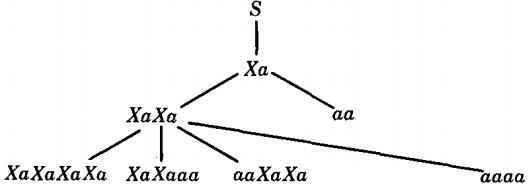
It is clear what is happening. All words in the language have only a's as letters.

All working strings have an even number of symbols (terminals plus nonterminals).

The production S → Xa can be used only once in any derivation, from then on the working string has an even length.

The substitution X → XaX would keep an even-length string even just as X → a would.

So the final word must have an even number of letters in it, all a's. We must also show that all even-length strings of a's can be derived.

To do this, we can say, that to produce a²ⁿ we use S → Xa once, then X → XaX leftmost n - 1 times, and then X → a exactly n times.

For example, to produce a⁸ :

S ⇒ Xa ⇒ XaXa ⇒ XaXaXa ⇒XaXaXaXa ⇒ aaXaXaXa SaaaaXaXa ⇒ aaaaaaXa ⇒ a⁸

The union, the product, the Kleene closure, the complement, and the intersection of regular languages are all regular

In this section we prove that the union, the product, and the Kleene closure of context-free languages are context-free. But the complement and intersection of context-free languages are not in general context-free.

THEOREM 30 If L₁ and L₂ are context-free languages, then their union, L₁ + L₂, is also a context-free language. In other words, the context-free languages are closed under union.

PROOF 1 (by Grammars)

Let L₁ be PALINDROME. One CFG for L₁ is

S → aSa | bSb | a | b | Λ

Let L₂ be {aⁿbⁿ where n ≥ 0. One CFG for L₂ is

S → aSb | Λ

Theorem recommends the following CFG for L₁ + L₂:

S → S₁ | S₂
S₁ → aS₁a | bS₁b | a | b | Λ
S₂ → aS₂b | Λ

One CFG for the language EVENPALINDROME is

S → aSa | bSb | Λ

One CFG for the language ODDPALINDROME is

S → aSa | bSb | a | b

Using the algorithm of the proof above we produce the following CFG for PALINDROME:

PALINDROME = EVENPALINDROME + ODDPALINDROME

S → S₁ | S₂
S₁ → aS₁a | bS₁b | Λ
S₂ → aS₂a | bS₂b | a | b

We have seen more economical grammars for this language before

Let L₁ be PALINDROME over the alphabet Σ₁ = {a,b}, while L₂ is {cⁿdⁿ where n ≥ 0} over the alphabet Σ₂ = {c,d}.

Then one CFG that generates L₁ + L₂ is:

S → S₁ | S₂
S₁ → aS₁a | bS₁b | a | b | Λ
S₂ → cS₂d | Λ

This is a language over the alphabet {a,b,c,d}

Since L₁ and L₂ are context-free languages, we know that there is a PDA1 that accepts L₁ and a PDA₂ that accepts L₂.

We can construct a PDA₃ that accepts the language of L₁ + L₂ by amalgamating the START states of these two machines.

This means that we draw only one START state and from it come all the edges that used to come from either prior START state.

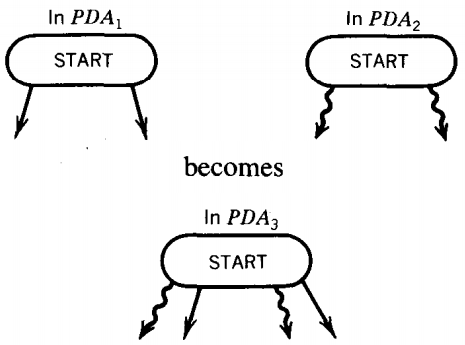
Once an input string starts on a path on this combined machine, it follows the path either entirely within PDA₁ or entirely within PDA₂ since there are no cross-over edges.

Any input reaching an ACCEPT state has been accepted by one machine or the other and so is in L₁ or in L₂.

Also any word in L₁ + L₂ can find its old path to acceptance on the subpart of PDA₃ that resembles PDA₁ or PDA₂.

Consider these two machines:

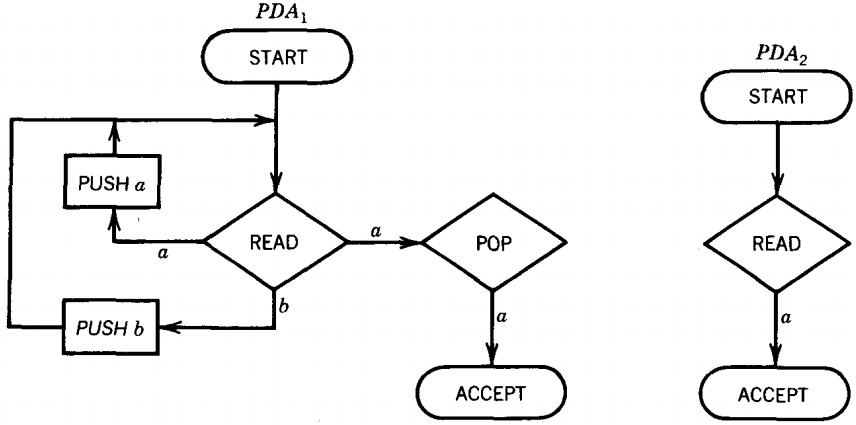
PDA₁ accepts the language of all words that contain a double a. PDA₂ accepts all words that begin with an a. The machine for L₁ + L₂ is:

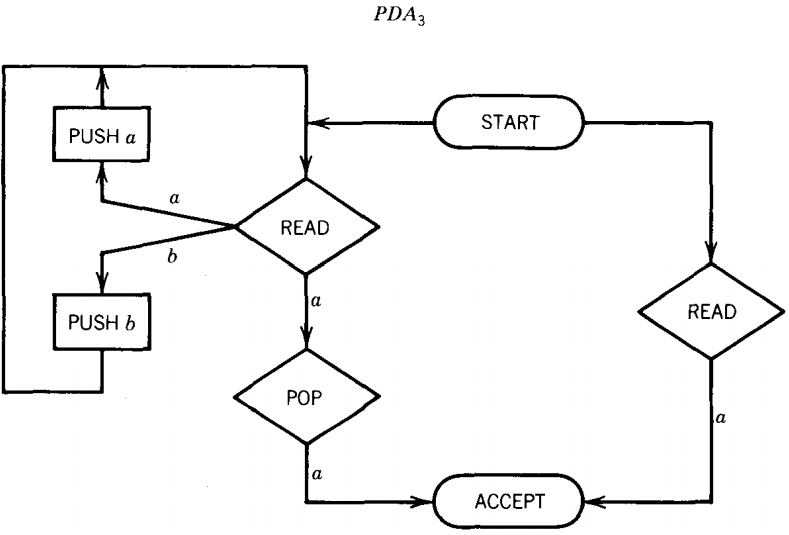
Notice that we have drawn PDA₃ with only one ACCEPT state by combining the ACCEPT states from PDA₁ and PDA₂.

This was not mentioned in the algorithm in the proof, but it only simplifies the picture without changing the substance of the machine.

If L₁ and L₂ are context-free languages, then so is L₁L₂. In other words, the context-free languages are closed under product.

PROOF 1 (by Grammars)

Let L₁ be PALINDROME and CFG₁ be

S → aSa | bSb | a | b | Λ

Let L₂ be {aⁿbⁿ where n ≥ 0} and CFG₂ be

S → aSb | Λ

The algorithm in the proof recommends the CFG:

S → S₁S₂
S₁ → aS₁a | bS₁b | a | b | Λ
S₂ → aS₂b | Λ

for the language L₁L₂

If L is a context-free language, then L* is one too. In other words, the contextfree languages are closed under Kleene star.

Let us start with a CFG for the language L. As always, the start symbol for this language is the symbol S.

Let us as before change this symbol (but no other nonterminals) to S₁ throughout the grammar.

Let us then add to the list of productions the new production:

S → S₁S | Λ

Now we can, by repeated use of this production, start with S and derive:

S ⇒ S₁S ⇒ S₁S₁S ⇒ S₁S₁S₁S ⇒ S₁S₁S₁S₁S ⇒ S₁S₁S₁S₁S₁S ⇒ S₁S₁S₁S₁S₁S₁

Following each of these S₁'s independently through the productions of the original CFG, we can form any word in L* made up of five concatenated words from L.

To convince ourselves that the productions applied to the various separate word factors do not interfere in undesired ways we need only think of the derivation tree.

Each of these S₁'s is the root of a distinct branch.

The productions along one branch of the tree do not effect those on another.

Similarly, any word in L* can be generated by starting with enough copies of S₁.

If the CFG is

S → aSa | bSb | a | b | Λ

(which generates PALINDROME), then one possible CFG for PALINDROME* is

S → XS | Λ
X → aXa | bXb | a | b | Λ

Notice that we have used the symbol X instead of the nonterminal S₁, which was indicated in the algorithm in the proof. Of course, this makes no difference.