INTERSECTION AND COMPLEMENT - UPSC FEVER

We proved that the union, product, and Kleene star closure of context-free languages are also context-free. This left open the question of intersection and complement.

THEOREM : The intersection of two context-free languages may or may not be contextfree.

All regular languages are context-free (Theorem 19). The intersection of two regular languages is regular (Theorem 12). Therefore, if L, and L2 are regular and context-free then

L₁ ∩ L₂ is both regular and context-free.

Let L₁ = {aⁿbⁿa^m, where n, m = 1 2 3 ... but n is not necessarily the same as m} = {aba abaa aabba ... }

To prove that this language is context-free, we present a CFG that generates it.

S → XA
X → aXb | ab
A → aA | a

We could alternately have concluded that this language is context-free by observing that it is the product of the CFL {aⁿbⁿ} and the regular language aa*

Let L₂ = {aⁿbⁿa^m, where n, m = 1 2 3 but n is not necessarily the same as m} = {aba aaba abbaa . . . }

Be careful to notice that these two languages are different. To prove that this language is context-free, we present a CFG that generates it:

S → AX
X → aXb | ab
A → aA | a

Alternately we could observe that L, is the product of the regular language aa* and the CFL {bⁿaⁿ}.

Both languages are context-free, but their intersection is the language L₃ = L₁ ∩ L₂ = {aⁿbⁿaⁿ for n = 1 2 3 . . .}

since any word in both languages has as many starting a's as middle b's (to be in L₁) and as many middle-b's as final a's (to be in L₂).

But we proved that this language L₃ is non-context-free. Therefore, the intersection of two context-free languages can be non-contextfree.

If L₁ and L₂ are two CFL's and if L₁ is contained in L₂, then the intersection is L₁ again, which is still context-free, for example,

L₁ = {aⁿ for n = 1 2 3 ...}

L₂ = PALINDROME

L₁ is contained in L₂; therefore, L₁ ∩ L₂ = L₁

which is context-free.

Notice that in this example we do not have the intersection of two regular languages since PALINDROME is nonregular.

Let: L₁ = PALINDROME L₂ = language of a⁺b⁺a⁺ = language of aa*bb*aa*

In this case, L₁ ∩ L₂ is the language of all words with as many final a's as initial a's with only b's in between.

L₁ ∩ L₂ = {aⁿb^maⁿ n,m = 1 2 3 ... where n is not necessarily equal to m} = {aba abba aabaa aabbaa ... }

This language is still context-free since it can be generated by this grammar:

S → aSa | aBa
B → bB | b

or accepted by this PDA:

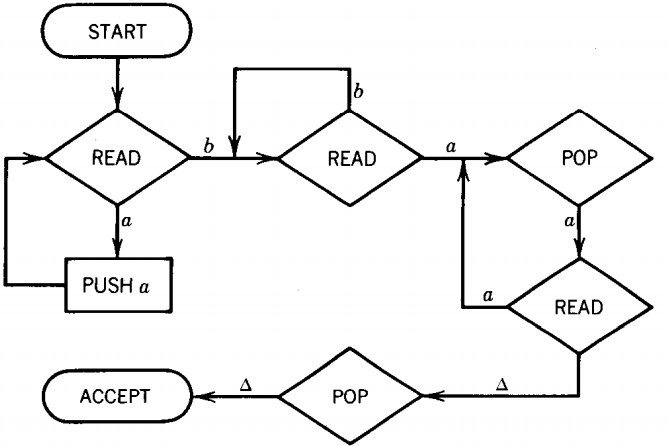
First, all the front a's are put into the STACK. Then the b's are ignored. Then we alternately READ and POP a's till both the INPUT TAPE and STACK run out simultaneously.

Again note that these languages are not both regular (one is, one is not).

Let L₁ be the language

EQUAL = all words with the same number of a's and b's

We know this language is context-free because we have seen a grammar that generates it:

S → bA | aB
A → bAA | aS | a
B → aBB | bS | b

Let L₂ be the language L₂ = {aⁿb^maⁿ n,m = 1 2 3... n = m or n ≠ m}

The language L₂ was shown to be context-free in the previous example. Now: L₃ = L₁ ∩ L₂ = {aⁿb²ⁿaⁿ for n = 1 2 3 ... } = {abba aabbbbaa ...

To be in L₁ = EQUAL, the b-total must equal the a-total, so there are 2n b's in the middle if there are n a's in the front and in the back.

We use the Pumping Lemma to prove that this language is non-context-free.

As always, we observe that the sections of the word that get repeated cannot contain the substrings ab or ba, since all words in L₃ have exactly one of each substring.

This means that the two repeated sections (the v-part and ypart) are each a clump of one solid letter. If we write some word w of L₃ as : w=uvxyz

then we can say of v and y that they are either all a's or all b's or one is A. However, if one is solid a's, that means that to remain a word of the form aⁿb^maⁿ the other must also be solid a's since the front and back a's must remain equal.

But then we would be increasing both clumps of a's without increasing the b's, and the word would then not be in EQUAL.

If neither v nor y have a's, then they increase the b's without the a's and again the word fails to be in EQUAL.

Therefore, the Pumping Lemma cannot apply to L₃, so L₃ is non-contextfree.

If L is regular, then L' is also regular and both are context-free.

This is one of our few proofs by indirect argument.
Suppose the complement of every context-free language were context-free.

Then if we started with two such languages, L₁ and L₂, we would know that L₁' and L₂' are also context-free. Furthermore, L₁' + L₂' would have to be context free.

Not only that but, (L₁' + L₂')' would also have to be context-free, as the complement of a context-free language.

But, (L₁' + L₂')' = L₁ ∩ L₂ and so the intersection of L₁ and L₂ must be context-free.

But L₁ and L₂ are any arbitrary CFL's, and therefore all intersections of context-free languages would have to be context-free.

But by the previous theorem we know that this is not the case. Therefore, not all context-free languages have context-free complements.

All regular languages have been covered in the proof above. There are also some nonregular but context-free languages that have context-free complements.

One example is the language of palindromes with an X in the center, PALINDROMEX. This is a language over the alphabet {a, b, X}.

= {w X reverse(w), where w is any string in (a + b)*} = {X aXa bXb aaXaa abXba baXab bbXbb . . . }

This language can be accepted by a deterministic PDA such as the one below:

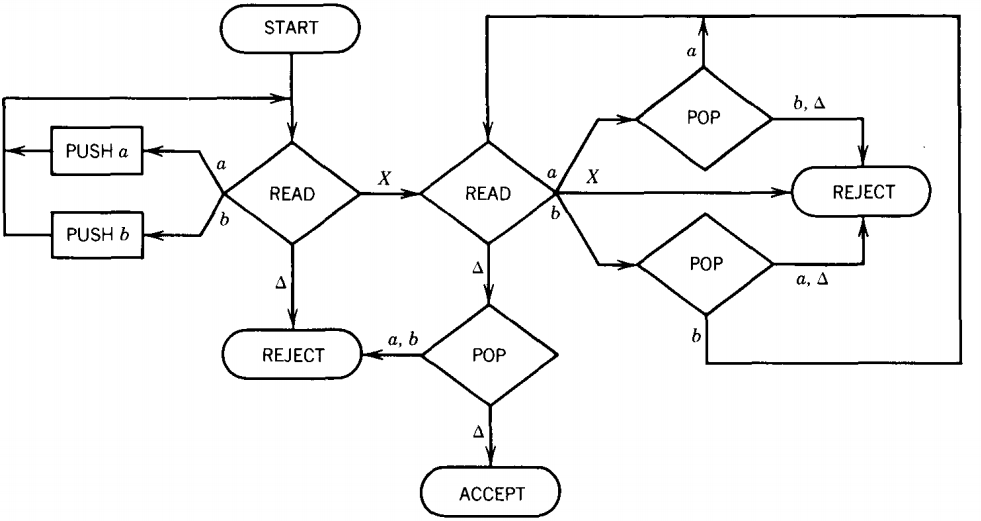
Since this is a deterministic machine, every input string determines some path from START to a halt state, either ACCEPT or REJECT.

We have drawn in all possible branching edges so that no input crashes.

The strings not accepted all go to REJECT. In every loop there is a READ statement that requires a fresh letter of input so that no input string can loop forever.

(This is an important observation, although there are other ways to guarantee no infinite looping.)

To construct a machine that accepts exactly those input strings that this machine rejects, all we need to do is reverse the status of the halt states from ACCEPT to REJECT and vice versa.

This is the same trick we pulled on FA's to find machines for the complement language.

In this case, the language L' of all input strings over the alphabet Σ = {a, b, X} that are not in L is simply the language accepted by:

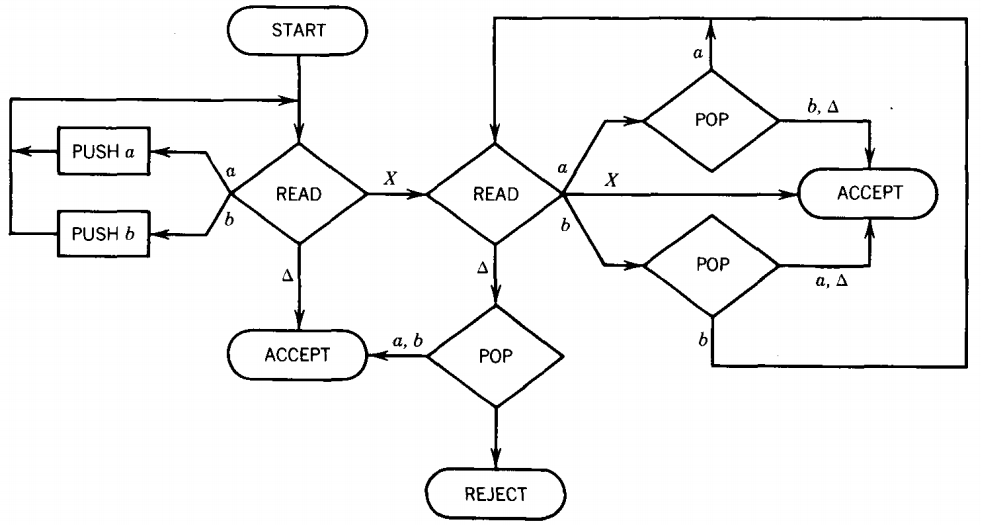
We may wonder why this trick cannot be used to prove that the complement of any context-free language is context-free, since they all can be defined by PDA's. The answer is nondeterminism.

If we have a nondeterministic PDA then the technique of reversing the status of the halt states fails.

Remember that when we work with nondeterministic machines we say that any word that has some path to ACCEPT is in the language of that machine.

In a nondeterministic PDA a word may have two possible paths, the first of which leads to ACCEPT and the second of which leads to REJECT.

We accept this word since there is at least one way it can be accepted. Now if we reverse the status of each halt state we still have two paths for this word: the first now leads to REJECT and the second now leads to ACCEPT.

Again we have to accept this word since at least one path leads to ACCEPT.

The same word cannot be in both a language and its complement, so the halt-status-reversed PDA does not define the complement language.

Let us be more concrete about this point. The following (nondeterministic) PDA accepts the language NON NULL EVEN PALINDROME:

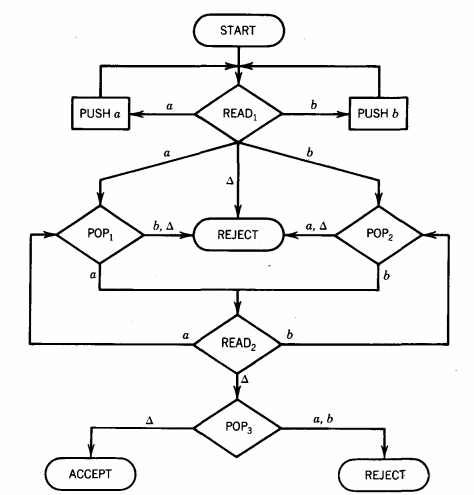
We have drawn this machine so that, except for the nondeterminism at the first READ, the machine offers no choice of path, and every alternative is labeled. All input strings lead to ACCEPT or REJECT, none crash or loop forever.

Let us reverse the status of the halt states to create this PDA

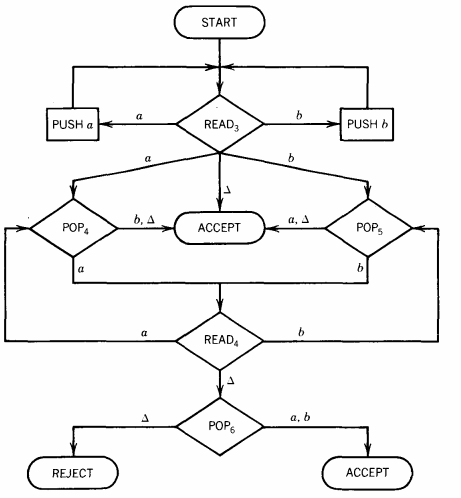
The word abba can be accepted by both machines. To see how it is accepted by the first PDA, we trace its path.

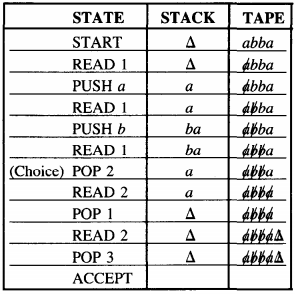
To see how it can be accepted by the second PDA we trace this path:

There are many more paths this word can take in the second PDA that also lead to acceptance. Therefore halt-state reversal does not always change a PDA for L into a PDA for L'

A deterministic PDA (DPDA) is a PDA for which every possible input string corresponds to a unique path through the machine. If we further require that no input loops forever, we say that we have a DPDA that always stops. Not all languages that can be accepted by PDA's can be accepted by a DPDA that always stops.

PROOF

The language L defined in the previous example is one such language. It can be generated by CFG's, so it can be accepted by some PDA.

Yet if it were acceptable by any deterministic PDA that always stops, then its complement would have to be context-free, since we could build a PDA for the complement by reversing ACCEPT and REJECT states.

However, the complement of this language is not a context-free language.

Therefore, no such deterministic machine for L exists.

L can be accepted by some PDA but not by any DPDA that always stops.

The intersection of a context-free language with a regular language is always context-free.

PROOF

Let C be a context-free language that is accepted by the PDA, P. Let R be a regular language that is accepted by the FA, F.

We now show how to take P and F and construct a PDA from them called A that will have the property that the language that A accepts is exactly C ∩ R.

The method will be very similar to the method we used to build the FA to accept the union of two regular languages.

Before we start, let us assume P reads the whole input string before accepting.

If the states of F are called x₁, x₂, ... and the READ and POP states of P are called y₁, y₂ .... then the new machine we want to build will have states labeled "x_i and y_j," meaning that the input string would now be in state xi if running on F and in state y_j if running on P.

We do not have to worry about the PUSH states of P since no branching takes place there. At a point in the processing when the PDA A wants to accept the input string, it must first consult the status of the current simulated x-state.

If this x-state is a final state, the input can be accepted because it is accepted on both machines. This is a general theoretical discussion.

Let us now look at an example. Let C be the language EQUAL of words with the same total number of a's and b's. Let the PDA to accept this language be

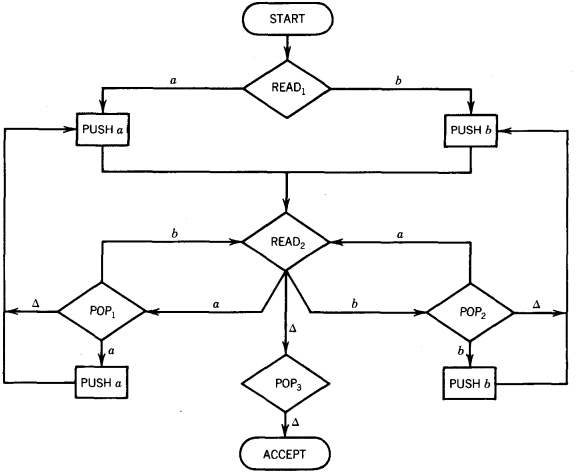
This is a new machine to us, so we should take a moment to dissect it. At every point in the processing the STACK will contain whichever letter has been read more, a or b, and will contain as many of that letter as the number of extra times it has been read.

If we have read from the TAPE six more b's than a's, then we shall find six b's in the STACK.

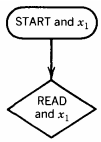
If the STACK is empty at any time, it means an equal number of a's and b's have been read. The process begins in START and then goes to READ₁.

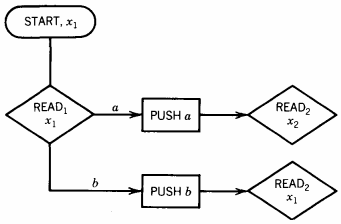
Whatever we read in READ₁ is our first excess letter and is pushed onto the STACK. The rest of the input string is read in READ₂.

If during the processing we read an a, we go and consult the STACK. If the STACK contains excess b's, then one of them will be cancelled against the a we just read, POP₁ - READ₂.

If the STACK is empty, then the a just read is pushed onto the STACK as a new excess letter. If the STACK is found to contain a's already, then we must replace the one we popped out for testing as well as add the new one just read to the amount of total excess in the STACK.

In all, two a's must be pushed onto the STACK. When we are finally out of input letters in READ₂, we go to POP₃ to be sure there are no excess letters being stored in the STACK.

Then we accept. This machine reads the entire INPUT TAPE before accepting and never loops forever.

Let us intersect this with the FA below that accepts all words ending in the letter a

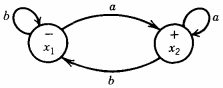
Now let us manufacture the joint intersection machine. We cannot move out of x₁ until after the first READ in the PDA.

At this point in the PDA we branch to separate PUSH states each of which takes us to READ₂. However, depending on what is read in READ₁, we will either want to be in "READ₂ and x₁" or "READ₂ and x₂," so these must be two different states:

From "READ₂ and x₂" if we read an a we shall have to be in "POP₁ and x₂," whereas if we read a b we shall be in "POP₂ and x₁."

In this particular machine, there is no need for "POP₁ and x₁" since POP₁ can only be entered by reading an a and x₁ can only be entered by reading a b. For analogous reasons, we do not need a state called "POP₂ and x₂" either.

We shall eventually need both "POP₃ and x₁" and "POP₃ and x₂" because we have to keep track of the last input letter.

Even if "POP₃ and x₁" should happen to pop a △, it cannot accept since x₁ is not a final state and so the word ending there is rejected by the FA. The whole machine looks like this.

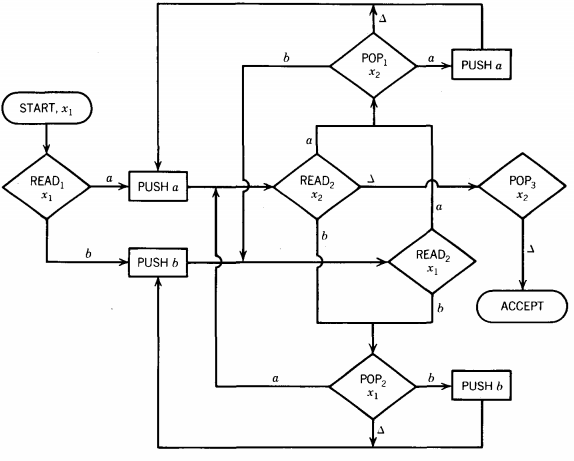
We did not even bother drawing "POP₃ X₁." If a blank is read in "READ₂, x₁" the machine peacefully crashes.

This illustrates the technique for intersecting a PDA with an FA. The process is straightforward.

Let us consider the language DOUBLEWORD:

DOUBLEWORD = {ww where w is an string of a's and b's}
= {Λ aa bb aaaa abab baba bbbb aaaaaa . . . }

Let us assume for a moment that DOUBLEWORD were a CFL.

Then when we intersect it with any regular language, we must get a context-free language.

Let us intersect DOUBLEWORD with the regular language defined by aa*bb*aa*bb*

A word in the intersection must have both forms, this means it must be ww where w = anbm for some n and m = 1 2 3...

This observation may be obvious, but we shall prove it anyway.

If w contained the substring ba, then ww would have two of them, but all words in aa*bb*aa*bb* have exactly one such substring.

Therefore, the substring ba must be the crack in between the two w's in the form ww.

This means w begins with a and ends with b.

Since it has no ba, it must be aⁿb^m. The intersection language is therefore: {aⁿb^maⁿb^m}

But we showed in the last chapter that this language was non-context-free. Therefore, DOUBLEWORD cannot be context-free either.