INTRODUCTION

• A set of elements is any collection of object s usually having a common property. It is denoted by y ∈ S or y ∉ S




• A set with a denumerable number of elements is specified by braces: A = {1, 2, 3, 4} indicates that the elements of set A are the numbers 1, 2, 3, and 4




• Closure: The set of natural numbers N = {1,2,3,4...} is closed with respect to operator '+' as for any a,b ∈ N there exists a unique c ∈ N such that a + b = c. Similarly the set of N is not Closed with respect to operator '-' as 2 - 3 = -1 which ∉ N even though 2, 3 ∈ N.

Two Valued Boolean Algebra

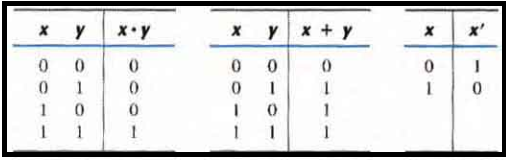
• Boolean algebra is an algebraic structure defined by a set of elements, B, together with two binary operators '+' and '-' , provided that the following postulates are satisfied




• The structure has to be closed with respect to the two operators. This is seen in above tables as all outputs are 0 / 1 and 0, 1 ∈ B.




• Identity law: Its valid here as 0 + 0 = 0, 0 + 1 = 1 + 0 = 1; 1 . 1 = 1; 1 . 0 = 0 . 1 = 0




• Commutative laws: They are also valid




• Complement laws: As x * x' = 0 and x + x' = 1 so the laws are valid.




• Boolean algebra follows the above postulates.

Postulates of Boolean Algebra

• x + 0 = x ; x . 1 = x




• x + x' = 1 ; x . x' = 0




• x + x = x ; x . x = x




• x + 1 = x ; x . 0 = 0




• Involution: (x')' = x




• Commutative: x + y = y + x ; x . y = y . x




• Associative: x + (y + z) = (x + y) + z; x(yz) = (xy)z




• Distributive: x(y + z) = xy + xz; x + yz = (x + y)(x + z)




• DeMorgan: (x + y)' = x'y' ; (xy)' = x' + y'




• Absorption: x + xy = x; x(x + y) = x

Operator Precedence in Boolean Algebra

• The operator precedence for evaluating Boolean expressions is (I) Parenthesis, (II) NOT, (III) AND, (IV) OR.




• Thus, expressions inside the parenthesis are evaluated first followed by Complement, AND and finally OR.

BOOLEAN FUNCTIONS

• A Boolean function described by an algebraic expression consists of binary variables, the constants 0 and 1, and the logic operation symbols.




• A Boolean function expresses the logical relationship between binary variables and is evaluated by determining the binary value of the expression for all pos­sible values of the variables.




• If 'n' variables are present in the expression then the rows in the truth table are 2ⁿ.




• A Boolean function can be transformed from an algebraic expression into a circuit diagram composed of logic gates connected in a particular structure.




• There is only one way that a Boolean function can be represented in a truth table. However when the function is in algebraic form it can be expressed in a variety of ways, all of which have equivalent logic.




• By manipulating a Boolean expression according to the rules of Boolean algebra it is sometimes possible to obtain a simpler expression for the same function and thus reduce the number of gates in the circuit and the number of inputs to the gate.

Simplification of Boolean Expressions

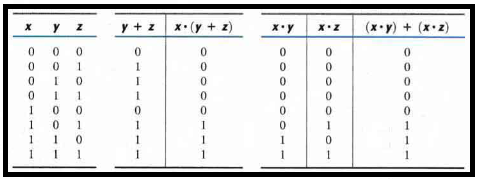
• Consider the following Boolean function:




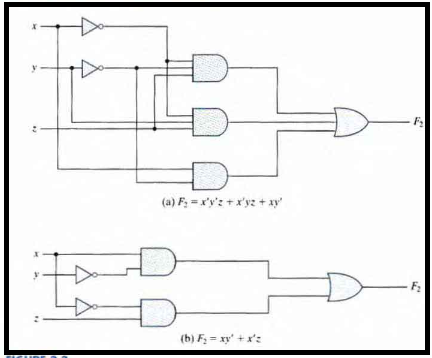
• F₂ = x'y'z + x'yz + xy'




• This can be simplified by using the identities:




• F₂ = x'z(y' + y) + xy'




• F₂ = x'z + xy'




• The original and the new circuit diagram

Simplify x (x' + y)

• = xx' + xy




• = 0 + xy




• = xy

Simplify x + (x'y)

• = (x+x')(x+y)




• = 1(x+y)




• = x + y

Simplify (x+y)(x+y')

• = x+xy+xy'+yy'




• = x + (1+y+y')




• = x

Simplify xy + x'z + yz

• = xy + x'z + yz(x + x')




• = xy + x'z + xyz + x'yz




• = xy(1+z) + x'z(1+y)




• = xy + x'z

Complement of a Function

• The complement of a function F is F' and is obtained from an interchange of 0's for 1's and 1's for 0's in the value of F



• (A + B)' = A'B'



• (A.B)' = A' + B'




• (A+B+C)' = A'B'C'




• The generalized form of De-Morgan' s theorems states that the complement of a function is obtained by interchanging AND and OR operators and complementing each literal.




• (A + B + C + ... + F)' = A'B'C'...F'




• (A.B.C...F)' = A' + B' + C' + ... + F'

Find complement of a Function F₁ = x'yz' + x'y'z

1. So we have F'₁ = (x'yz' + x'y'z)'

2. = (x'yz')'(x'y'z)'

3. = (x + y' + z)(x + y + z')

Find complement of a Function F₂ = x(y'z' + yz)

1. So we have F'₂ = [x(y'z' + yz)]'

2. = x' + (y'z' + yz)'

3. = x' + (y'z')'(yz)'

4. = x' + (y+z)(y'+z')

5. = x' + yz' + y'z

Complement of a Function - Dual Method

• Convert every AND to OR in the boolean expression.




• Complement each literal in the expression.

F₁ = x'yz' + x'y'z

1. The dual of F₁ = (x'+y+z')(x'+y'+z)

2. Complement of each literal: (x+y'+z)(x+y+z') = F'₁

F₂ = x(y'z' + yz)

1. The dual of F₂ = x + (y'+z')(y+z)

2. Complement of each literal: x' + (y+z)(y'+z') = F'₂

CANONICAL AND STANDARD FORMS

• A binary variable may appear eit her in its normal form (x) or in its complement form (x').




• Consider two variables 'x' and 'y' combined in an AND operation. Since we have two variables we get four combinations: xy, x'y', xy', x'y. We call (x') as ("x primed"). A variable in minterm is primed if its value is 0 otherwise it is unprimed.




• Each of these four AND terms are called Minterms or Standard Product.Thus 'n' variables can form 2ⁿ minterms. Any Boolean function can be expressed as a sum of minterms.




• In similar fashion, 'n' variables form an OR term with 2ⁿ possible combinations called Maxterms or Standard Sums




• Each maxterm is complement of the corresponding minterm




• A variable in maxterm is primed if its value is 1 otherwise it is unprimed.




• A Boolean function can be expressed algebraically from a given truth table by forming a minterrn for each combination of the variables that produces a '1' in the function and then tak­ing the OR of all those terms. Any Boolean function can be expressed as a product of maxterms

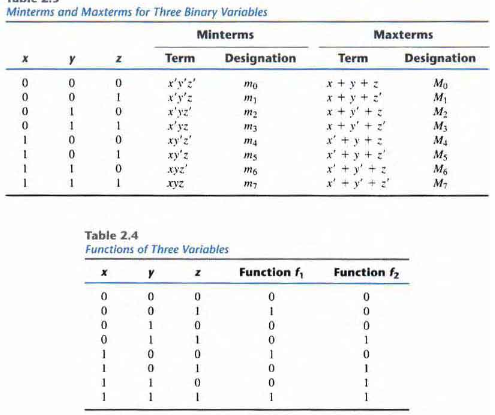
F₁ = x'y'z + xy'z' + xyz

1. From the table above we obtain F₁ = m₁ + m₄ + m₇

F₂ = x'yz + xy'z + xyz' + xyz

1. From the table above we obtain F₁ = m₃ + m₅ + m₆ + m₇

F₁ = (x+y+z)(x+y'+z)(x'+y+z')(x'+y'+z)

1. From the table above we obtain F₁ = M₀ . M₂ . M₃ . M₅ . m₆

Sum of Minterms

Q: F = A + B'C

1. The term has three variables: A,B,C and he first part of the expression 'A' has two variables missing viz. B and C

2. So, A = A(B + B') = AB + AB'

3. It still has one variable missing

4. AB + AB' = AB(C + C') + AB'(C + C')

5. = ABC + ABC' + AB'C + AB'C'

6. Now the second term of the expression is BC'

7. B'C = B'C(A + A') = B'CA + B'CA'

8. So we have F = ABC + ABC' + AB'C + AB'C' + B'CA + B'CA'

9. But AB'C appears twice so finally we get

10. F = ABC + ABC' + AB'C' + B'CA + B'CA'

11. F = m₁ + m₄ + m₅ + m₆ + m₇

12. A more convenient form isF = ∑(1, 4, 5, 6, 7)

Product of Maxterms

Solve F = xy + x'z

1. First, convert the func­tion into OR terms by using the distributive law: x + yz = (x + y)(x + z)

2. So we have, F = xy + x'z = (xy + x')(xy + z)

3. = (x + x')(y + x')(x + z)(y + z)

4. = (x' + y)(x + z)(y + z)

5. The function has three variables: x, y, and z. Each OR term is missing one variable; therefore,

6. x' + y = x' + y +zz' = (x' + y + z)(x' + y + z')

7. x + z = x + z + yy' = (x + y + z)(x + y' + z)

8. y + z = y + z + xx' = (x + y + z)(x' + y + z)

9. Combining all the terms and removing those which appear more than once, we finally obtain

10. F = (x + y + z)(x + y' + z)(x' + y + z)(x' + y + z')

11. Which is same as F = M₀M₂M₄M₅

12. F = ∏(0, 2, 4, 5)

Previous

Next