Storage and File Structure
Storage of a relation can be done either in sorted order or unsorted order.
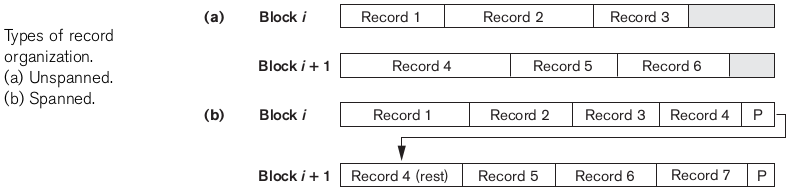
Spanned or Unspanned mapping :
In spanned mapping as seen above , if a particular record has no space to be stored fully in one block. Then we divide and store it partially. This means more efficiency and no internal fragmentation.
Unspanned mapping causes internal fragmentation as a particular record is stored only if it can be stored fully in a block otherwise it is moved to the next block.
However as blocks are many and it is more time consuming to search for a block in memory rather than searching for records in block.
When we use spanned mapping we save memory but more time is consumed in searching for a record as multiple blocks might have it.
In unspanned mapping we might waste memory but we can search faster as a record is stored in a single block.
| Sorted Order | Unsorted Order |
|---|---|
| Searching fast as records are sorted and order is known. | Searching is slow as we proceed to search linearly as no other information is known about order. |
| Insertion and deletion is difficult. As file is sorted and we have to find the exact position to insert. Similarly if we insert we need to push all records that come after it to new positions. Deletion also means that all other records shall have their addresses updated. | Insertion and deletion is easy. Insertion can be made anywhere (either first or last position). Deletion is easy if we want to delete any record. However to delete a specific record (most cases) it is difficult. |
| Records are inserted in an order that is sorted order on the basis of a single attribute / column o the table. | Random order is followed and any record can be placed anywhere. |
 >
>Indexing in DBMS
Database-system indices play the same role as book indices in libraries. For example, to retrieve a student record given an ID, the database system would look up an index to find on which disk block the corresponding record resides, and then fetch the disk block, to get the appropriate student record.
There are two basic kinds of indices:
Ordered indices : Based on a sorted ordering of the values.
Hash indices : Based on a uniform distribution of values across a range of buckets. The bucket to which a value is assigned is determined by a function, called a hash function.
Ordered Indices
The records in the indexed file may themselves be stored in some sorted order, just as books in a library are stored according to some attribute
A file may have several indices, on different search keys.
If the file containing the records is sequentially ordered, a clustering index OR Primary index is an index whose search key also defines the sequential order of the file.
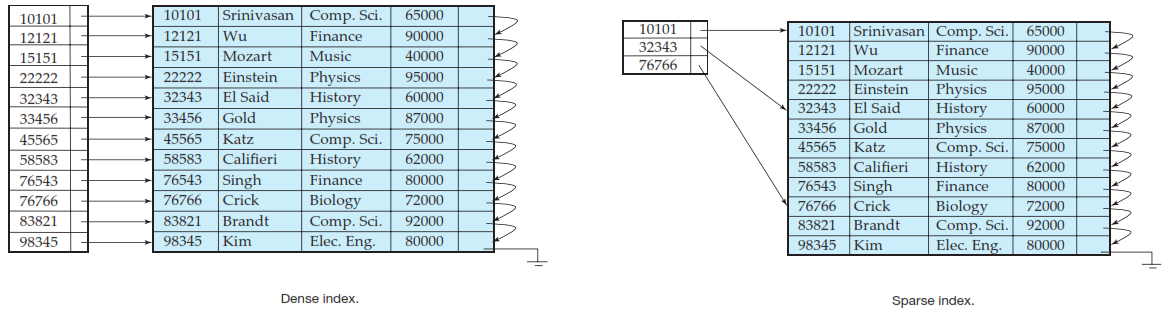
Dense and Sparse Indices :
In a dense index, an index entry appears for every search-key value in the file.
In a sparse index, an index entry appears for only some of the search-key values. Sparse indices can be used only if the relation is stored in sorted order of the search key
Dense and Sparse Indices :
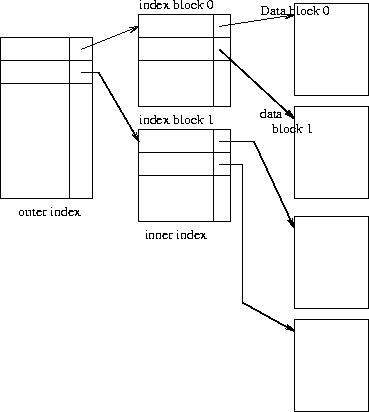
Multilevel Indices
If an index is small enough to be kept entirely in main memory, the search time to find an entry is low. However, if the index is so large that not all of it can be kept in memory, index blocks must be fetched from disk when required.
The search for an entry in the index then requires several disk-block reads.
To solve this we use multilevel indices:
We treat the index just as a sequential file, and construct a sparse outer index on the original index, which we now call the inner index.
To locate a record, we first use binary search on the outer index to find the record for the largest search-key value less than or equal to the one that we desire.
The pointer points to a block of the inner index.
The pointer in this inner index record points to the block of the file that contains the record for which we are looking.
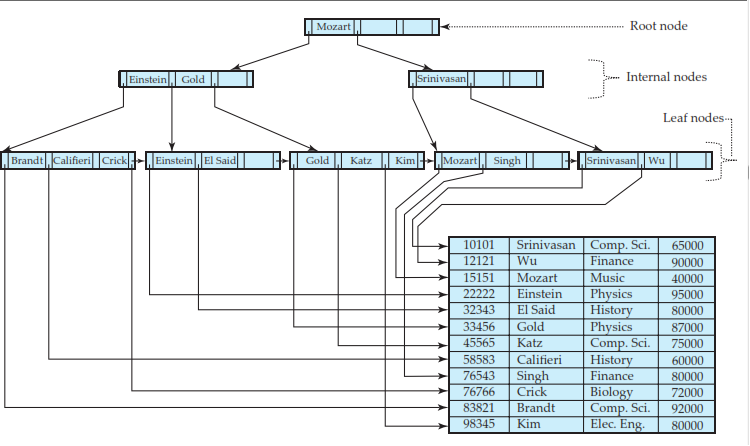
B+ - Tree Indexing
The B+ tree index structure is the most widely used of several index structures that maintain their efficiency despite insertion and deletion of data.
The B+tree index takes the form of a balanced tree in which every path from the root of the tree to a leaf of the tree is of the same length.
Each nonleaf node in the tree has between (n/2) and n children, where n is fixed for a particular tree.
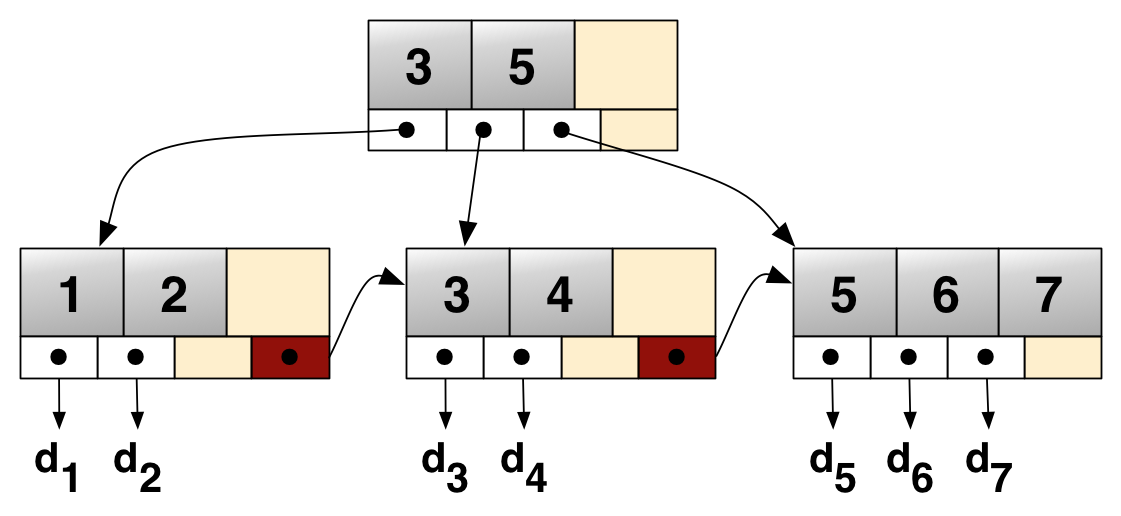
B+ - Tree Indexing for instructor file (n = 4).
A typical B+ tree node contains (n-1) key values and 'n' pointers. The search key values are in sorted order.
Each leaf can hold up to (n − 1) values. Leaf nodes to contain as few as upper-bound (n − 1)/2 values. With n = 4 in our example B+ tree, each leaf must contain at least 2 values, and at most 3 values.
The ranges of values in each leaf do not overlap. Also if Li and Lj are leaf nodes and i < j , then every search-key value in Li is less than or equal to every search-key value in Lj.
The nonleaf nodes of the B+ - tree form a multilevel (sparse) index on the leaf nodes.
The structure of nonleaf nodes is the same as that for leaf nodes, except that all pointers are pointers to tree nodes.
A nonleaf node may hold up to n pointers, and must hold at least upper-bound (n/2) pointers.
Unlike other nonleaf nodes, the root node can hold fewer than upper-bound (n/2) pointers; however, it must hold at least two pointers.
For a node containing m pointers (m ≤ n). For i = 2, 3,...,m − 1, pointer Pi points to the subtree that contains search-key values less than Ki and greater than or equal to Ki-1.
Pointer Pm points to the part of the subtree that contains those key values greater than or equal to Km-1 ,and pointer P1 points to the part of the subtree that contains those search-key values less than K1.
Processing a query in B+ Tree
In processing a query, we traverse a path in the tree from the root to some leaf node.
If there are N records in the file, the path is no longer than ⌈log⌈n/2⌉(N)⌉ N = records, n = poiner in a leaf.
Example : With n = 100, if we have 1 million search-key values in the file, a lookup requires: ⌈log⌈(100/2)⌉(1000000)⌉ = 4
If a Balanced Binary tree is used then there are N records in the file, the path is no longer than ⌈log2(N)⌉ N = records.
Example : If we have 1 million search-key values in the file, a lookup requires: ⌈log(2)(1000000)⌉ = 20
Insertion and Deletions in B+ Tree
The operations require I/O that is proportional to height of the tree.
⌈log⌈n/2⌉(N)⌉