Set Operations
Complement : Let U be the universal set. The complement of the set A, denoted by A, is the complement of A with respect to U. Therefore, the complement of the set A is U − A.
A ={x ∈ U | x ∉ A}.
Let A = {a, e, i, o, u} (where the universal set is the set of letters of the English alphabet). Then A = {b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w,x,y,z}.
Let A be the set of positive integers greater than 10 (with universal set the set of all positive integers). Then A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Note : A − B = A ∩ B.
Set Identities
| Identity | Name |
|---|---|
| A ∩ U = A | Identity laws |
| A ∪ ∅ = A | Identity laws |
| A ∪ U = U | Domination laws |
| A ∩ ∅ = ∅ | Domination laws |
| A ∪ A = A | Idempotent laws |
| A ∩ A = A | Idempotent laws |
| (A) = A | Complementation law |
| A ∪ B = B ∪ A | Commutative laws |
| A ∩ B = B ∩ A | Commutative laws |
| A ∪ (B ∪ C) = (A ∪ B) ∪ C | Associative laws |
| A ∩ (B ∩ C) = (A ∩ B) ∩ C | Associative laws |
| A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | Distributive laws |
| A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) | Distributive laws |
| (A ∩ B) = (A) ∪ (B) | De Morgan’s laws |
| (A ∪ B) = (A) ∩ (B) | De Morgan’s laws |
| A ∪ (A ∩ B) = A | Absorption laws |
| A ∩ (A ∪ B) = A | Absorption laws |
| A ∪ A = U | Complement laws |
| A ∩ A = ∅ | Complement laws |
Functions
Let "A" and "B" be nonempty sets. A function f from "A" to "B" is an assignment of exactly one element of "B" to each element of "A". We write f(a) = b if "b" is the unique element of "B" assigned by the function 'f' to the element a of A. If f is a function from A to B, we write f : A → B.
Remark : Functions are sometimes also called mappings or transformations
Domain and Codomain of a function
If f is a function from A to B, we say that "A" is the domain of "f" and "B" is the codomain of f.
If f(a) = b, we say that "b" is the image of "a" and "a" is a preimage of "b".
The range, or image, of f is the set of all images of elements of A. Also, if f is a function from A to B, we say that f maps A to B.
Two functions are equal when they have the same domain, have the same codomain, and map each element of their common domain to the same element in their common codomain
Q. What are the domain, codomain, and range of the function that assigns grades to students described in the first paragraph of the introduction of this section?
Let G be the function that assigns a grade to a student in our discrete mathematics class. Note that G(Adams) = A, for instance.
The domain of G is the set {Adams, Chou, Goodfriend, Rodriguez, Stevens}, and the codomain is the set {A, B, C, D, F}.
The range of G is the set {A, B, C, F}, because each grade except D is assigned to some student.
Q. Let R be the relation with ordered pairs (Abdul, 22), (Brenda, 24), (Carla, 21), (Desire, 22), (Eddie, 24), and (Felicia, 22). Here each pair consists of a graduate student and this student’s age. Specify a function determined by this relation
If f is a function specified by R, then f(Abdul ) = 22, f(Brenda) = 24, f(Carla) = 21, f(Desire) = 22, f(Eddie) = 24, and f(Felicia) = 22.
For the domain, we take the set {Abdul, Brenda, Carla, Desire, Eddie, Felicia}.
A co-domain needs to contain all possible ages of students. Because it is highly likely that all students are less than 100 years old, we can take the set of positive integers less than 100 as the codomain
The range of the function we have specified is the set of different ages of these students, which is the set {21, 22, 24}.
Q. Let f be the function that assigns the last two bits of a bit string of length 2 or greater to that string. For example, f(11010) = 10. Then, the domain of f is the set of all bit strings of length 2 or greater, and both the codomain and range are the set {00, 01, 10, 11}.
Let f : Z → Z assign the square of an integer to this integer. Then, f(x) = x2.
Here the domain of f is the set of all integers, the codomain of f is the set of all integers, and the range of f is the set of all integers that are perfect squares, namely, {0, 1, 4, 9,...}.
Q. The domain and codomain of functions are often specified in programming languages. For instance, the Java statement int floor(float real){...} and the C++ function statement int function (float x){...}
The domain of the floor function is the set of real numbers (represented by floating point numbers) and its codomain is the set of integers.
A function is called real-valued if its codomain is the set of real numbers, and it is called integer-valued if its codomain is the set of integers.
Two real-valued functions or two integer valued functions with the same domain can be added, as well as multiplied.
Definition 3: Function
Let f1 and f2 be functions from A to R. Then f1 + f2 and f1 . f2to R defined for all x ∈ A by
(f1 + f2)(x) = f1(x) + f2(x)
(f1 . f2)(x) = f1(x) . f2(x)
Q. f1 and f2 be functions from R to R such that f1(x) = x2 and f2(x) = x - x2. What are the functions (f1 + f2)(x) and (f1 . f2)(x)
(f1 + f2)(x) = f1(x) + f2(x)
= x2 + x - x2
= x
Step 2:
(f1 . f2)(x) = f1(x) . f2(x)
= x2 . ( x - x2)
= x3 - x4
DEFINITION 4
Let f be a function from A to B and let S be a subset of A. The image of S under the function f is the subset of B that consists of the images of the elements of S.
Example : Let A = {a, b, c, d, e} and B = {1, 2, 3, 4} with f(a) = 2, f(b) = 1, f(c) = 4, f(d) = 1, and f(e) = 1. The image of the subset S = {b, c, d} is the set f(S) = {1, 4}.
One-to-One and Onto Functions
Some functions never assign the same value to two different domain elements. These functions are said to be one-to-one or injective.
We can express that f is one-to-one using quantifiers as ∀a∀b(f (a) = f(b) → a = b) or equivalently ∀a∀b(a ≠ b → f(a) ≠ f(b)), where the universe of discourse is the domain of the function.
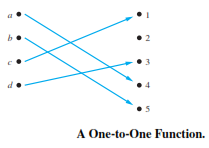
Q. Determine whether the function f from {a, b, c, d} to {1, 2, 3, 4, 5} with f(a) = 4, f(b) = 5, f(c) = 1, and f(d) = 3 is one-to-one
The function f is one-to-one because f takes on different values at the four elements of its domain.
Q. Determine whether the function f(x) = x2 from the set of integers to the set of integers is one-to-one.
The function f(x) = x2 is not one-to-one because, for instance, f(1) = f(−1) = 1, but 1 ≠ −1.
Increasing and Decreasing functions :
Increasing : ∀x∀y(x < y → f(x) ≤ f(y))
Strictly increasing : ∀x∀y(x < y → f (x) < f (y))
Decreasing : ∀x∀y(x < y → f(x) ≥ f(y))
Strictly decreasing : ∀x∀y(x < y → f (x) > f (y))
Surjective Functions
A function f from A to B is called onto, or a surjection if and only if for every element b ∈ B there is an element a ∈ A with f(a) = b.
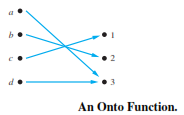
Q. Let f be the function from {a, b, c, d} to {1, 2, 3} defined by f(a) = 3, f(b) = 2, f(c) = 1, and f(d) = 3. Is f an onto function?
Because all three elements of the codomain are images of elements in the domain, we see that f is onto.
Note that if the codomain were {1, 2, 3, 4}, then f would not be onto.
Q. Is the function f(x) = x2 from the set of integers to the set of integers onto?
The function f is not onto because there is no integer x with x2 = −1.
Q. Is the function f(x) = x + 1 from the set of integers to the set of integers onto?
This function is onto, because for every integer y there is an integer x such that f(x) = y. To see this, note that f(x) = y if and only if x + 1 = y, which holds if and only if x = y − 1.
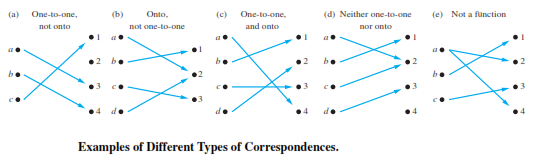
Function : one-to-one correspondence, or a bijection
The function f is a one-to-one correspondence, or a bijection, if it is both one-to-one and onto. We also say that such a function is bijective.
Q. Let f be the function from {a, b, c, d} to {1, 2, 3, 4} with f(a) = 4, f(b) = 2, f(c) = 1, and f(d) = 3. Is 'f' a bijection?
The function f is one-to-one and onto. It is one-to-one because no two values in the domain are assigned the same function value. It is onto because all four elements of the codomain are images of elements in the domain. Hence, f is a bijection
The identity function on A
Let A be a set. The identity function on A is the function tA : A → A where tA(x) = x for all x ∈ A.
So, the identity function tA is the function that assigns each element to itself.
The function tA is one-to-one and onto, so it is a bijection.
Suppose that f : A → B.
To show that f is injective : Show that if f(x) = f(y) for arbitrary x, y ∈ A with x ≠ y, then x = y.
To show that f is not injective Find particular elements x, y ∈ A such that x ≠ y and f(x) = f(y).
To show that f is surjective Consider an arbitrary element y ∈ B and find an element x ∈ A such that f(x) = y.
To show that f is not surjective Find a particular y ∈ B such that f(x) ≠ y for all x ∈ A