Inverse Functions and Compositions of Functions
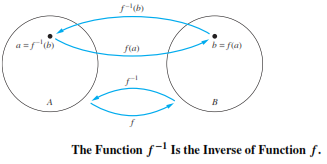
Let f be a one-to-one correspondence from the set A to the set B.
The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f(a) = b.
The inverse function of f is denoted by f−1(b) = a when f(a) = b.
If a function f is not a one-to-one correspondence, we cannot define an inverse function of f.
When f is not a one-to-one correspondence, either it is not one-to-one or it is not onto. If f is not one-to-one, some element b in the codomain is the image of more than one element in the domain.
If f is not onto, for some element b in the codomain, no element a in the domain exists for which f(a) = b.
Consequently, if f is not a one-to-one correspondence, we cannot assign to each element b in the codomain a unique element a in the domain such that f(a) = b (because for some b there is either more than one such a or no such a).
A one-to-one correspondence is called invertible because we can define an inverse of this function.
A function is not invertible if it is not a one-to-one correspondence, because the inverse of such a function does not exist.
Q. Let f be the function from {a, b, c} to {1, 2, 3} such that f(a) = 2, f(b) = 3, and f(c) = 1. Is f invertible, and if it is, what is its inverse?
The function f is invertible because it is a one-to-one correspondence. The inverse function f−1 reverses the correspondence given by f ,so f−1(1) = c, f−1(2) = a, and f−1(3) = b.
Q. Let f : Z → Z be such that f(x) = x + 1. Is f invertible, and if it is, what is its inverse?
The function f has an inverse because it is a one-to-one correspondence
To reverse the correspondence, suppose that y is the image of x, so that y = x + 1. Then x = y − 1. This means that y − 1 is the unique element of Z that is sent to y by f . Consequently, f−1(y) = y − 1.
Composition of the functions 'f' and 'g'
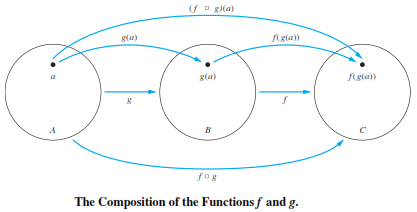
Let g be a function from the set A to the set B and let f be a function from the set B to the set C. The composition of the functions f and g, denoted for all a ∈ A by f ◦ g, is defined by
(f ◦ g)(a) = f (g(a)).
To find (f ◦ g)(a) we first apply the function g to a to obtain g(a) and then we apply the function f to the result g(a) to obtain (f ◦ g)(a) = f(g(a)).
Note that even though f ◦ g and g ◦ f are defined for the functions f and g, f ◦ g and g ◦ f are not equal. In other words, the commutative law does not hold for the composition of functions.
Q. Let g be the function from the set {a, b, c} to itself such that g(a) = b, g(b) = c, and g(c) = a. Let f be the function from the set {a, b, c} to the set {1, 2, 3} such that f(a) = 3, f(b) = 2, and f(c) = 1. What is the composition of f and g, and what is the composition of g and f ?
The composition f ◦ g is defined by (f ◦ g)(a) = f(g(a)) = f(b) = 2, (f ◦ g) (b) = f(g(b)) = f(c) = 1, and (f ◦ g)(c) = f(g(c)) = f(a) = 3
Q. Let f and g be the functions from the set of integers to the set of integers defined by f(x) = 2x + 3 and g(x) = 3x + 2. What is the composition of f and g? What is the composition of g and f ?
Both the compositions f ◦ g and g ◦ f are defined. Moreover,
(f ◦ g)(x) = f(g(x)) = f(3x + 2) = 2(3x + 2) + 3 = 6x + 7
and
(g ◦ f )(x) = g(f(x)) = g(2x + 3) = 3(2x + 3) + 2 = 6x + 11.
(f−1◦ f )(a) = f−1(f (a)) = f−1(b) = a
(f ◦ f−1)(b) = f(f−1(b)) = f(a) = b
The Graphs of Functions
Let f be a function from the set A to the set B. The graph of the function f is the set of ordered pairs {(a, b) | a ∈ A and f(a) = b}.
Q. Display the graph of the function f (n) = 2n + 1 from the set of integers to the set of integers.
The graph of f is the set of ordered pairs of the form (n, 2n + 1), where n is an integer.
Q. Display the graph of the function f(x) = x2 from the set of integers to the set of integers.
The graph of f is the set of ordered pairs of the form (x, f (x)) = (x, x2), where x is an integer.
Ceiling and Floor functions :
The floor function (greatest integer function) assigns to the real number x the largest integer that is less than or equal to x.
The value of the floor function at x is denoted by ⌊x⌋.
The ceiling function assigns to the real number x the smallest integer that is greater than or equal to x.
The value of the ceiling function at x is denoted by ⌈x⌉.
Example : ⌊1/2⌋ = 0; ⌈1/2⌉ = 1
Useful Properties of the Floor and Ceiling Functions
| Property of ceil | Property of floor |
|---|---|
| ⌈x⌉ = n if and only if n − 1 < x ≤ n | ⌊x⌋ = n if and only if n ≤ x < n+ 1 |
| ⌈x⌉ = n if and only if x ≤ n < x + 1 | ⌊x⌋ = n if and only if x − 1 < n ≤ x |
| x − 1 < ⌊x⌋ ≤ x ≤ ⌈x⌉ < x+ 1 | |
| ⌈-x⌉ = −⌈x⌉ | ⌊-x⌋ = − ⌊x⌋ |
| ⌈x + n⌉ = ⌈x⌉ + n | ⌊x + n⌋ = ⌊-x⌋ + n |
Sequences and Summations
A sequence is a discrete structure used to represent an ordered list. For example, 1, 2, 3, 5, 8 is a sequence with five terms and 1, 3, 9, 27, 81 ,... ,3n , ... is an infinite sequence.
A geometric progression is a sequence of the form a, ar2, ar3 ,..., arn where the initial term "a" and the common ratio "r" are real numbers.
An arithmetic progression is a sequence of the form a, a + d,a + 2d,...,a + nd where the initial term "a" and the common difference "d" are real numbers.
Sequences of the form a1, a2 ... an are often used in computer science. These finite sequences are also called strings. This string is also denoted by a a1, a2 ... an.
The length of a string is the number of terms in this string. The empty string, denoted by λ, is the string that has no terms. The empty string has length zero.
The sequences {sn} with sn = −1 + 4n and {tsn} with tsn = 7 − 3n are both arithmetic progressions with initial terms and common differences equal to −1 and 4, and 7 and −3, respectively, if we start at n = 0. The list of terms s1, s2, s3 ... sn
List "s" begins with −1, 3, 7, 11,...
List "t" begins with 7, 4, 1, −2,....
Recurrence Relations
A recurrence relation for the sequence {an} is an equation that expresses an in terms of one or more of the previous terms of the sequence, namely, a0, a1,...,an-1, for all integers n with n ≥ n0, where n0 is a nonnegative integer.
A sequence is called a solution of a recurrence relation if its terms satisfy the recurrence relation.
Q. Let {an} be a sequence that satisfies the recurrence relation an = an-1 + 3 for n = 1, 2, 3,..., and suppose that a0 = 2. What are a1, a2, and a3?
We see from the recurrence relation that a1 = a0 + 3 = 2 + 3 = 5
It then follows that a2 = 5 + 3 = 8 and a3 = 8 + 3 = 11.
Q. The Fibonacci sequence, f0 = 0, f1 = 1 and the recurrence relation fn = fn-1 + fn-2 for n = 2,3...
The recurrence relation for the Fibonacci sequence tells us that we find successive terms by adding the previous two terms. Because the initial conditions tell us that f0 = 0 and f1 = 1, using the recurrence relation in the definition we find that
f2 = f1 + f0
f3 = f2 + f1
f4 = f3 + f2
Important Summations

Cardinality of Sets
Cardinality of a finite set as the number of elements in the set.
The sets A and B have the same cardinality if and only if there is a one-to-one correspondence from A to B. When A and B have the same cardinality, we write |A| = |B|.
If there is a one-to-one function from A to B, the cardinality of A is less than or the same as the cardinality of B and we write |A| ≤ |B|. Moreover, when |A| ≤ |B| and A and B have different cardinality, we say that the cardinality of A is less than the cardinality of B and we write |A| < |B|.
Countable Sets
A set that is either finite or has the same cardinality as the set of positive integers is called countable.
A set that is not countable is called uncountable. When an infinite set S is countable, we denote the cardinality of S by ℵ0 (where ℵ is aleph).
We write |S| = ℵ0 and say that S has cardinality “aleph null.”
Q. Show that the set of odd positive integers is a countable set.
To show that the set of odd positive integers is countable, we will exhibit a one-to-one correspondence between this set and the set of positive integers. Consider the function f (n) = 2n − 1 from Z+ to the set of odd positive integers.
We show that f is a one-to-one correspondence by showing that it is both one-to-one and onto. To see that it is one-to-one, suppose that f (n) = f (m). Then 2n − 1 = 2m − 1, so n = m. To see that it is onto, suppose that t is an odd positive integer. Then t is 1 less than an even integer 2k, where k is a natural number. Hence t = 2k − 1 = f(k).
Q. Show that the set of all integers is countable.
We can list all integers in a sequence by starting with 0 and alternating between positive and negative integers: 0, 1, −1, 2, −2,.... Alternatively, we could find a one-to-one correspondence between the set of positive integers and the set of all integers.
The function f(n) = n/2 when n is even and f(n) =−(n−1)/2 when n is odd is such a function. Consequently, the set of all integers is countable.
Useful Theorems
If A and B are countable sets, then A ∪ B is also countable.
If A and B are sets with |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|. In other words, if there are one-to-one functions f from A to B and g from B to A, then there is a one-to-one correspondence between A and B.
A function is computable if there is a computer program in some programming language that finds the values of this function. If a function is not computable we say it is uncomputable.
Matrices
A matrix is a rectangular array of numbers. A matrix with m rows and n columns is called an m × n matrix. The plural of matrix is matrices. A matrix with the same number of rows as columns is called square.
Two matrices are equal if they have the same number of rows and the same number of columns and the corresponding entries in every position are equal.
Let A =[aij] and B =[bij] be m × n matrices. The sum of A and B, denoted by A + B, is the m × n matrix that has [aij + bij] as its (i, j)th element. In other words, A + B =[aij + bij].
Let A be an m × k matrix and B be a k × n matrix. The product of A and B, denoted by AB = [cij] then cij = ai1b1j + ai2b2j + ... + aikbkj
In general, suppose that A is an m × n matrix and B is an r × s matrix. Then AB is defined only when n = r and BA is defined only when s = m; AB and BA are not necessarily equal
The identity matrix of order n is the n × n matrix In =[δ ij], where δij = 1 if i = j and δij = 0 if i ≠ j.
The transpose of A, denoted by A' , is the n × m matrix obtained by interchanging the rows and columns of A.
A square matrix A is called symmetric if A = A'. Thus A =[aij] is symmetric if aij = aji for all i and j with 1 ≤ i ≤ n and 1 ≤ j ≤ n.
A matrix all of whose entries are either 0 or 1 is called a zero–one matrix.
Let A =[aij] and B =[bij] be m × n zero–one matrices. Then the join of A and B is the zero–one matrix with (i, j)th entry a . The join of A and B is denoted by Aij ∨ Bij. The meet of A and B is the zero–one matrix with (i, j)th entry aij ∨ bij. The meet of A and B is denoted by Aij ∧ Bij.
Let A =[aij] be an m × k zero–one matrix and B =[bij] be a k × n zero–one matrix. Then the Boolean product of A and B, denoted by A &exnor; B, is the m × n matrix with (i, j)th entry cij where cij = (ai1 ∧ b1j) ∨ (ai2 ∧ b2j) ∨ ... ∨ (aik ∧ bkj)
Let A be a square zero–one matrix and let r be a positive integer. The rth Boolean power of A is the Boolean product of r factors of A. The rth Boolean product of A is denoted by A[r].