Expected Value and Variance
The expected value of a random variable is a weighted average of the values of a random variable.
Variance, which tells us how spread out the values of this random variable are
The expected value, also called the expectation or mean, of the random variable X on the sample space S is equal to E(X) = ∑ s ∈ S p(s)X(s)
The deviation of X at s ∈ S is X(s) − E(X), the difference between the value of X and the mean of X
The expected number of successes when "n" mutually independent Bernoulli trials are performed, where "p" is the probability of success on each trial, is np.
Q. Let X be the number that comes up when a fair die is rolled. What is the expected value of X?
The random variable X takes the values 1, 2, 3, 4, 5, or 6, each with probability 1/6. It follows that
E(X) = 1/ 6 · 1 + 1/ 6 · 2 + 1/ 6 · 3 + 1/ 6 · 4 + 1/ 6 · 5 + 1/ 6 · 6 = 21/ 6 = 7/ 2 .
Q. A fair coin is flipped three times. Let S be the sample space of the eight possible outcomes, and let X be the random variable that assigns to an outcome the number of heads in this outcome. What is the expected value of X?
The values of X are the eight possible outcomes when a coin is flipped three times
Because the coin is fair and the flips are independent, the probability of each outcome is 1/8
E(X) = 1/ 8 [X(HHH) + X(HHT) + X(HTH) + X(THH) + X(TTH) +X(THT) + X(HTT) + X(TTT)]
= 1 / 8 (3 + 2 + 2 + 2 + 1 + 1 + 1 + 0)
= 12 / 8
= 3 / 2
Q. What is the expected value of the sum of the numbers that appear when a pair of fair dice is rolled?
Let X be the random variable equal to the sum of the numbers that appear when a pair of dice is rolled. The value of X for the 36 outcomes of this experiment.
The range of X is {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
p(X = 2) = p(X = 12) = 1/36,
p(X = 3) = p(X = 11) = 2/36 = 1/18,
p(X = 4) = p(X = 10) = 3/36 = 1/12,
p(X = 5) = p(X = 9) = 4/36 = 1/9
p(X = 6) = p(X = 8) = 5/36
p(X = 7) = 6/36 = 1/6
E(X) = 2 * 1/36 + 3 * 1/18 + 4 * 1/12 + 5 * 1/9 + 6 * 5/ 36 + 7 * 1/6 + 8 * 5/36 + 9 * 1/9 + 10 * 1/12 + 11 * 1/18 + 12 * 1/36
= 7
Relations and Their Properties
Let A and B be sets. A binary relation from A to B is a subset of A × B.
A binary relation from "A" to "B" is a set "R" of ordered pairs where the first element of each ordered pair comes from "A" and the second element comes from "B".
The notation a R b is used to denote that (a, b) ∈ R. Moreover, when (a, b) belongs to R, "a" is said to be related to "b" by R
Binary relations represent relationships between the elements of two sets.
Example of binary relations :
Let "A" be the set of students in your school, and let "B" be the set of courses. Let "R" be the relation that consists of those pairs (a, b), where "a" is a student enrolled in course "b".
So assume Sanjay dutt is also enrolled in CS510, then the pair (Sanjay dutt, CS510) is in R.
However, if Sharukh Khan is not enrolled in CS510, then the pair (Sharukh Khan, CS510) is not in R.
Note that if a student is not currently enrolled in any courses there will be no pairs in "R" that have this student as the first element. Similarly, if a course is not currently being offered there will be no pairs in "R" that have this course as their second element.
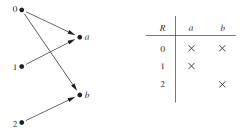
Q. Let A ={0, 1, 2} and B ={a, b}. Then {(0, a), (0, b), (1, a), (2,b)} is a relation from A to B.
This means, for instance, that 0 R a, but that 1 R b. Relations can be represented graphically,
as shown in Figure below, using arrows to represent ordered pairs. Another way to represent this
relation is to use a table, which is also done in Figure below.
Relations on a Set
A relation on a set A is a relation from A to A.
Q. Let A be the set {1, 2, 3, 4}. Which ordered pairs are in the relation R ={(a, b) | a divides b}?
Because (a, b) is in R if and only if a and b are positive integers not exceeding 4 such that a divides b, we see that
R ={(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}.
Q. Consider these relations on the set of integers: R 1 = {(a, b) | a ≤ b}, R 2 = {(a, b) | a > b}, R 3 = {(a, b) | a = b or a = −b}, R 4 = {(a, b) | a = b}, R 4 = {(a, b) | a = b + 1}, R 5 = {(a, b) | a + b ≤ 3}. Which of these relations contain each of the pairs (1, 1), (1, 2), (2, 1), (1, −1), and (2, 2)?
The pair (1, 1) is in R 1, R 3, R 4 and R 6; (1, 2) is in R 1 and R 6; (2, 1) is in R 2, R 5 and R 6
(1, −1) is in R2, R3 , and R6; and
finally, (2, 2) is in R1, R3 and R4 .
Q. How many relations are there on a set with n elements?
A relation on a set "A" is a subset of A × A.
Because A × A has n2 elements when "A" has "n" elements, and a set with "m" elements has 2m subsets, there are 2n2 subsets of A × A.
Thus, there are 2n2 relations on a set with "n" elements.
For example, there are 232 = 29 = 512 relations on the set {a, b, c}.
Properties of Relations
Reflexive relations : A relation R on a set A is called reflexive if (a, a) ∈ R for every element a ∈ A.
Symmetric and Anti-Symmetric relations : A relation R on a set "A" is called symmetric if (b, a) ∈ R whenever (a, b) ∈ R, for all (a, b ∈ A). A relation R on a set A such that for all a, b ∈ A, if (a, b) ∈ R and (b, a) ∈ R, then a = b is called anti-symmetric.
Transitive relations : A relation R on a set A is called transitive if whenever (a, b) ∈ R and (b, c) ∈ R, then (a, c) ∈ R, for all a, b, c ∈ A.
Q. Consider the following relations on {1, 2, 3, 4}: R1 ={(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)}, R 2 ={(1, 1), (1, 2), (2, 1)}, R 3 ={(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)}, R 4 ={(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}, R 5 ={(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}, R 6 ={(3, 4)}. Which of these relations are reflexive?
The relations R 3 and R 5 are reflexive because they both contain all pairs of the form (a, a), namely, (1, 1), (2, 2), (3, 3), and (4, 4).
The other relations are not reflexive because they do not contain all of these ordered pairs. In particular, R 1 , R 2 , R 4 , and R 6 are not reflexive because (3, 3) is not in any of these relations.
Q. Is the “divides” relation on the set of positive integers reflexive?
Because a | a whenever a is a positive integer, the “divides” relation is reflexive.
(Note that if we replace the set of positive integers with the set of all integers the relation is not reflexive because by definition 0 does not divide 0.)
In some relations an element is related to a second element if and only if the second element is also related to the first element. The relation consisting of pairs (x, y), where x and y are students at your school with at least one common class has this property.
Q. How many reflexive relations are there on a set with n elements?
A relation R on a set A is a subset of A × A.
Consequently, a relation is determined by specifying whether each of the n 2 ordered pairs in A × A is in R
However, if R is reflexive, each of the n ordered pairs (a, a) for a ∈ A must be in R.
Each of the other n(n − 1) ordered pairs of the form (a, b), where a ≠ b, may or may not be in R.
Hence, by the product rule for counting, there are 2n(n−1) reflexive relations
Q. R1 ={(a, b) | a ≤ b}, R2 ={(a, b) | a > b}, R3 ={(a, b) | a = b or a = −b}, R4 ={(a, b) | a = b}, R5 ={(a, b) | a = b + 1}, R6 ={(a, b) | a + b ≤ 3}. Which of these relations are symmetric and which are antisymmetric?
R3 is symmetric as if a = b or a = -b then b = a or b = -a.
R4 is symmetric as a = b implies that b = a
R6 is symmetric because a + b ≤ 3 implies that b + a ≤ 3.
R1 is anti-symmetric as the inequalities a ≤ b and b ≤ a imply that a = b
R2 is anti-symmetric because it is possible that a > b and b > a
R4 is antisymmetric, because two elements are related with respect to R4 if and only if they are equal.
R5 is antisymmetric because it is impossible that a = b + 1 and b = a + 1.
Q. Consider the following relations on {1, 2, 3, 4}: R1 ={(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)}, , R 4 ={(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}. Which of these relations are transitive?
R4 is transitive, because (3, 2) and (2, 1), (4, 2) and (2, 1), (4, 3) and (3, 1), and (4, 3) and (3, 2) are the only such sets of pairs, and (3, 1), (4, 1), and (4, 2) belong to R4
R1 is not transitive because (3, 4) and (4, 1) belong to R1 , but(3, 1) does not.
Q. Is the “divides” relation on the set of positive integers transitive?
Suppose that a divides b and b divides c.
Then there are positive integers k and l such that b = ak and c = bl. Hence, c = a(kl),soa divides c
It follows that this relation is transitive.
Combining Relations
Let A = {1, 2, 3} and B = {1, 2, 3, 4}. The relations R1 = {(1, 1), (2, 2), (3, 3)} and R2 ={(1, 1), (1, 2), (1, 3), (1, 4)} can be combined to obtain :-
R1 ∪ R2 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (3, 3)}
R1 ∩ R2 = {(1, 1)}
R1 - R2 = {(2, 2), (3, 3)}
R2 - R1 = {(1, 2), (1, 3), (1, 4)}
Q. Let A and B be the set of all students and the set of all courses at a school, respectively. Suppose that R1 consists of all ordered pairs (a, b), where "a" is a student who has taken course "b", and R2 consists of all ordered pairs (a, b), where "a" is a student who requires course "b" to graduate. What are the relations R1 ∩ R2, R1 ∪ R2, R1 ⊕ R2, R1 - R2 and R2 - R1 ?
R1 ∪ R2 consists of all ordered pairs (a, b), where a is a student who either has taken course b or needs course b to graduate.
R1 ∩ R2 is the set of all ordered pairs (a, b), where a is a student who has taken course b and needs this course to graduate.
R1 ⊕ R2 consists of all ordered pairs (a, b), where student a has taken course b but does not need it to graduate or needs course b to graduate but has not taken it.
R1 - R2 is the set of ordered pairs (a, b), where a has taken course b but does not need it to graduate; that is, b is an elective course that a has taken.
R2 - R1 is the set of all ordered pairs (a, b), where b is a course that a needs to graduate but has not taken.