Binary Tree Data Structure

Unlike Arrays, Linked Lists, Stack and queues, which are linear data structures, trees are hierarchical data structures.

The topmost node is called root of the tree. The elements that are directly under an element are called its children. The element directly above something is called its parent.

Applications of Trees are :

Manipulate hierarchical data.

Trees provide moderate access/search (quicker than Linked List and slower than arrays)

Trees provide moderate insertion/deletion (quicker than Arrays and slower than Unordered Linked Lists).

Like Linked Lists and unlike Arrays, Trees don’t have an upper limit on number of nodes as nodes are linked using pointers.

Binary Tree Representation in C : A tree is represented by a pointer to the topmost node in tree. If the tree is empty, then value of root is NULL. A Tree node contains following parts.

Data

Pointer to left child

Pointer to right child

struct node 
{
  int data;
  struct node *left;
  struct node *right;
};

Properties of binary tree

The maximum number of nodes at level ‘n’ of a binary tree is 2^n-1

Maximum number of nodes in a binary tree of height ‘h’ is 2^h – 1.

In a Binary Tree with "N" nodes, minimum possible height or minimum number of levels is ⌈ Log₂(N+1) ⌉

A Binary Tree with "L" leaves has at least ⌈ Log₂L ⌉ + 1 levels.

In Binary tree, number of leaf nodes is always one more than nodes with two children.

Types of Binary Tree

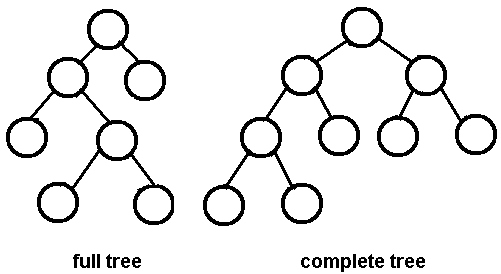
Full Binary Tree : A Binary Tree is full if every node has 0 or 2 children. Following are examples of full binary tree. We can also say a full binary tree is a binary tree in which all nodes except leaves have two children. In a Full Binary, number of leaf nodes is number of internal nodes plus 1

Complete Binary Tree : A Binary Tree is complete Binary Tree if all levels are completely filled except possibly the last level and the last level has all keys as left as possible

Perfect Binary Tree : A Binary tree is Perfect Binary Tree in which all internal nodes have two children and all leaves are at same level. A Perfect Binary Tree of height h (where height is number of nodes on path from root to leaf) has 2^h – 1 node.

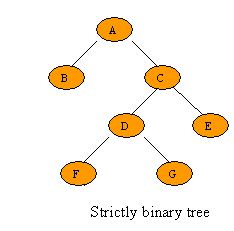
A full binary tree (sometimes proper binary tree or 2-tree or strictly binary tree) : is a tree in which every node other than the leaves has two children. So you have no nodes with only 1 child. Appears to be the same as strict binary tree.

Balanced Binary Tree : A binary tree is balanced if height of the tree is O(Log n) where n is number of nodes. For Example, AVL tree maintain O(Log n) height by making sure that the difference between heights of left and right subtrees is 1. Red-Black trees maintain O(Log n) height by making sure that the number of Black nodes on every root to leaf paths are same and there are no adjacent red nodes. Balanced Binary Search trees are performance wise good as they provide O(log n) time for search, insert and delete.

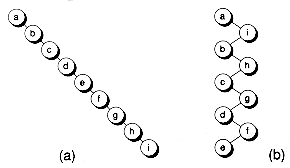
A degenerate (or pathological) tree : A Tree where every internal node has one child. Such trees are performance-wise same as linked list.

Binary Search Tree

Binary Search Tree, is a node-based binary tree data structure which has the following properties :

left child node is smaller than its parent Node i.e. The left subtree of a node contains only nodes with keys lesser than the node’s key

right child node is greater than its parent Node i.e. The right subtree of a node contains only nodes with keys greater than the node’s key.

The left and right subtree each must also be a binary search tree. There must be no duplicate nodes.

The above properties of Binary Search Tree provide an ordering among keys so that the operations like search, minimum and maximum can be done fast. If there is no ordering, then we may have to compare every key to search a given key.

Binary Search Tree

The search binary tree data structure supports many dynamic-set operations, including SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT,and DELETE. Thus, we can use a search tree both as a dictionary and as a priority queue.

Basic operations on a binary search tree take time proportional to the height of the tree. For a complete binary tree with n nodes, such operations run in Θ(lg n). If the tree is a linear chain of n nodes, however, the same operations take Θ(n) worst-case time.

A tree by a linked data structure in which each node is an object. In addition to a key and satellite data, each node contains attributes left, right,and p that point to the nodes corresponding to its left child, right child and parent node respectively.

If a child or the parent is missing, the appropriate attribute contains the value NIL. The root node is the only node in the tree whose parent is NIL.

Binary search Tree property states that: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then y.key ≤ x.key. If y is a node in the right subtree of x,then y.key ≥ x.key.

The binary-search-tree property allows us to print out all the keys in a binary search tree in sorted order by a simple recursive algorithm, called an inorder tree walk. This algorithm is so named because it prints the key of the root of a subtree between printing the values in its left subtree and printing those in its right subtree. (Similarly, a preorder tree walk prints the root before the values in either subtree, and a postorder tree walk prints the root after the values in its subtrees.)

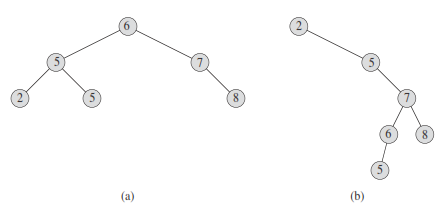
Binary Search Tree - Operations

```
INORDER-TREE-WALK(x)
```
```
if x ≠ NIL
```
```
    INORDER-TREE-WALK(x.left)
```
```
    print(x.key)
```
```
    INORDER-TREE-WALK(x.right)
```

If x is the root of an n-node subtree, then the call INORDER-TREE-WALK(x) takes Θ(n) time.

```
TREE-SEARCH(x,k)
```
```
if x ==NIL OR k == x.key
```
```
    return x
```
```
if k < x.key
```
```
   return TREE-SEARCH(x.left,k)
```
```
else return TREE-SEARCH(x.right,k)
```

Running time of TREE-SEARCH is O(h), where h is the height of the tree.

```
TREE-Minimum(x)
```
```
while x.left ≠ NIL
```
```
    x = x.left
```
```
return x
```

```
TREE-Maximum(x)
```
```
while x.right ≠ NIL
```
```
    x = x.right
```
```
return x
```

Running time of TREE-Minimum(x) and TREE-Minimum(x) is O(h), where h is the height of the tree.

```
TREE-Successor(x)
```
```
if x.right ≠ NIL
```
```
    return TREE-Minimum(x.right)
```
```
y = x.p
```
```
while y ≠ NIL and x == y.right
```
```
    x = y
```
```
    y = y.p
```
```
return y
```

Running time of TREE-Successor(x) and TREE-Predecessor(x) is O(h), where h is the height of the tree.

```
TREE-INSERT(T,z)
```
```
y = NIL
```
```
x = T.root
```
```
while x ≠ NIL
```
```
   y = x
```
```
   if z.key < x.key
```
```
      x = x.left
```
```
   else x = x.right
```
```
z.p = y 
```
```
if y == NIL 
```
```
   T.root = z
```
```
else if z.key < y.key 
```
```
   y.left = z
```
```
else y.right = z 
```

Like the other primitive operations on search trees, the procedure T REE-INSERT runs in O(h) time on a tree of height h.

Binary Search Tree - Deletion Operation

If z (node to be deleted) has no children, then we simply remove it by modifying its parent to replace z with NIL as its child.

If z has just one child, then we elevate that child to take z’s position in the tree by modifying z’s parent to replace z by z’s child.

If z has two children, then we ﬁnd z’s successor y — which must be in z’s right subtree - and have y take z’s position in the tree. The rest of z’s original right subtree becomes y’s new right subtree, and z’s left subtree becomes y’s new left subtree.

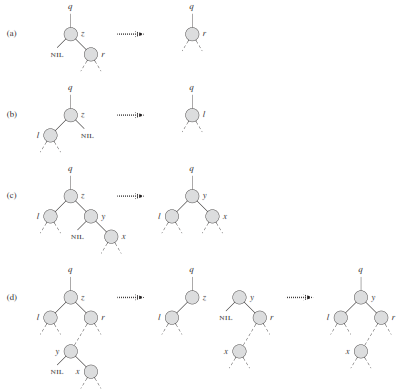
```
TREE-DELETE(T,z)
```
```
if z.LEFT == NIL
```
```
   TRANSPLANT(T,z,z.right)
```
```
elseif z.RIGHT == NIL
```
```
   TRANSPLANT(T,z,z.left)
```
```
else y = TREE-MINIMUM.(z.right)
```
```
   if y.p ≠ z
```
```
      TRANSPLANT(T,y,y.right)
```
```
      y.right = z.right
```
```
      y.right.p = y
```
```
   TRANSPLANT(T,z,y)
```
```
   y.left = z.left
```
```
   y.left.p = y
```

```
TRANSPLANT(T,u,v)
```
```
if u.p == NIL
```
```
   T.root = v
```
```
elseif u == u.p.left
```
```
   u.p.left = v
```
```
else u.p.right = v
```
```
if v ≠ NIL
```
```
   v.p = u.p
```

TREE-DELETE runs in O(h) time on a tree of height h.

Binary Tree Traversals - Inorder, Preorder, Postorder

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. Following are the generally used ways for traversing trees.

Inorder Traversal : In case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed, can be used.

Algorithm Inorder(tree)

Traverse the left subtree, i.e., call Inorder(left-subtree)

Visit the root.

Traverse the right subtree, i.e., call Inorder(right-subtree)

Preorder traversal : Preorder traversal is used to create a copy of the tree. Preorder traversal is also used to get prefix expression on of an expression tree.

Algorithm Preorder(tree)

Visit the root.

Traverse the left subtree, i.e., call Preorder(left-subtree)

Traverse the right subtree, i.e., call Preorder(right-subtree)

Postorder traversal : Postorder traversal is used to delete the tree.

Algorithm Postorder(tree)

Traverse the left subtree, i.e., call Postorder(left-subtree)

Traverse the right subtree, i.e., call Postorder(right-subtree)

Visit the root.

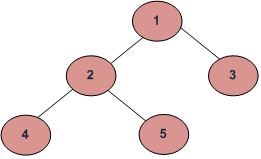
Q. Perform Inorder, Preorder and Postorder traversal of a binary search tree

Depth First Traversals :

Inorder (Left, Root, Right) : 4 2 5 1 3

Preorder (Root, Left, Right) : 1 2 4 5 3

Postorder (Left, Right, Root) : 4 5 2 3 1

Breadth First or Level Order Traversal : 1 2 3 4 5

upscfever.com