Error Detection and Correction
Networks must be able to transfer data from one device to another with acceptable accuracy. For most applications, a system must guarantee that the data received are identical to the data transmitted.
Any time data are transmitted from one node to the next, they can become corrupted in passage. Many factors can alter one or more bits of a message. Some applications require a mechanism for detecting and correcting errors.
Data can be corrupted during transmission. Some applications require that errors be detected and corrected.
Types of Errors
Whenever bits flow from one point to another, they are subject to unpredictable changes because of interference. This interference can change the shape of the signal. In a single-bit error, a 0 is changed to a 1 or a 1 to a 0. In a burst error, multiple bits are changed.
The term single-bit error means that only 1 bit of a given data unit (such as a byte, character, or packet) is changed from 1 to 0 or from 0 to 1. Single-bit errors are the least likely type of error in serial data transmission. To understand why, imagine data sent at 1 Mbps. This means that each bit lasts only 111,000,000 s, or 1 us. For a single-bit error to occur, the noise must have a duration of only 1 us, which is very rare; noise normally lasts much longer than this.
A burst error means that 2 or more bits in the data unit have changed. Note that a burst error does not necessarily mean that the errors occur in consecutive bits. The length of the burst is measured from the first corrupted bit to the last corrupted bit. Some bits in between may not have been corrupted.
Redundancy
The central concept in detecting or correcting errors is redundancy. To be able to detect or correct errors, we need to send some extra bits with our data. These redundant bits are added by the sender and removed by the receiver.
Their presence allows the receiver to detect or correct corrupted bits.
Detection Versus Correction :
In error detection, we are looking only to see if any error has occurred. The answer is a simple yes or no. We are not even interested in the number of errors. A single-bit error is the same for us as a burst error.
In error correction, we need to know the exact number of bits that are corrupted and more importantly, their location in the message. The number of the errors and the size of the message are important factors.
If we need to correct one single error in an 8-bit data unit, we need to consider eight possible error locations; if we need to correct two errors in a data unit of the same size, we need to consider 28 possibilities.
Forward Error Correction Versus Retransmission :
Forward error correction is the process in which the receiver tries to guess the message by using redundant bits.
This is possible if the number of errors is small.
Correction by re-transmission is a technique in which the receiver detects the occurrence of an error and asks the sender to resend the message.
Resending is repeated until a message arrives that the receiver believes is error-free (as usually, not all errors can be detected).
Coding
Redundancy is achieved through various coding schemes. The sender adds redundant bits through a process that creates a relationship between the redundant bits and the actual data bits.
The receiver checks the relationships between the two sets of bits to detect or correct the errors. The ratio of redundant bits to the data bits and the robustness of the process are important factors in any coding scheme.
Modular Arithmetic
In modular arithmetic, we use only a limited range of integers. We define an upper limit, called a modulus N. We then use only the integers 0 to N - 1, inclusive. This is modulo-N arithmetic.
For example, if the modulus is 12, we use only the integers 0 to 11, inclusive. An example of modulo arithmetic is our clock system. It is based on modulo-12 arithmetic, substituting the number 12 for 0. In a modulo-N system, if a number is greater than N, it is divided by N and the remainder is the result. If it is negative, as many Ns as needed are added to make it positive. Consider our clock system again. If we start a job at 11 A.M. and the job takes 5 h, we can say that the job is to be finished at 16:00 if we are in the military, or we can say that it will be finished at 4 P.M.
In Modulo - 2 Arithmetic :We can use only 0 and 1. Operations in this arithmetic are very simple. The following shows how we can add or subtract 2 bits.
Notice particularly that addition and subtraction give the same results. In this arithmetic we use the XOR (exclusive OR) operation for both addition and subtraction. The result of an XOR operation is 0 if two bits are the same; the result is 1 if two bits are different.
| Addition | Subtraction |
|---|---|
| 0 + 0 = 0 | 0 - 0 = 0 |
| 0 + 1 = 1 | 0 - 1 = 1 |
| 1 + 0 = 1 | 1 - 0 = 1 |
| 1 + 1 = 0 | 1 - 1 = 0 |
BLOCK CODING
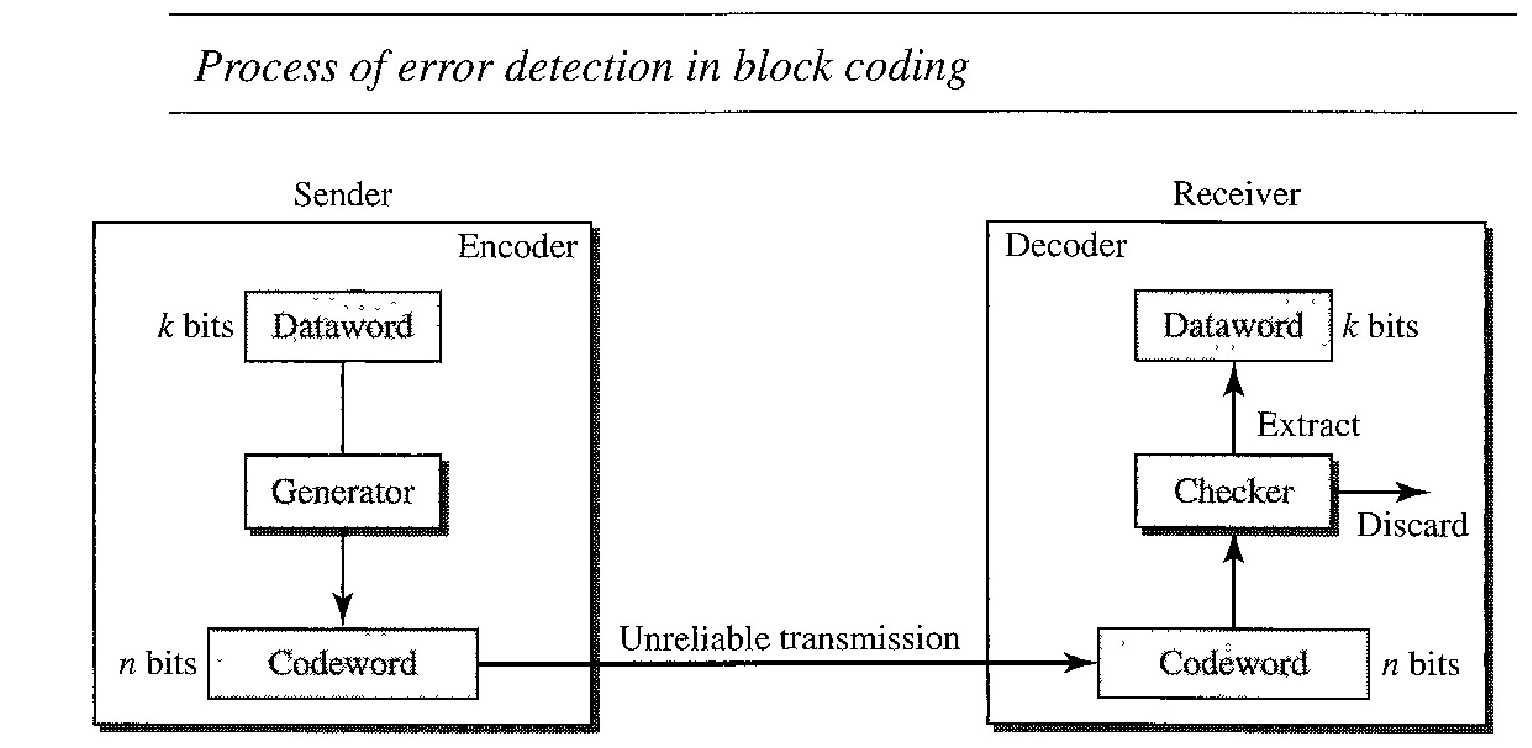
In block coding, we divide our message into blocks, each of "k" bits, called data words. We add "r" redundant bits to each block to make the length n = k + r. The resulting n-bit blocks are called codewords.
Now we have a set of datawords, each of size "k", and a set of codewords, each of size of "n". With "k" bits, we can create a combination of 2k datawords; with "n" bits, we can create a combination of 2n codewords.
Since n > k, the number of possible codewords is larger than the number of possible datawords. The block coding process is one-to-one; the same dataword is always encoded as the same codeword. This means that we have 2n - 2k codewords that are not used. We call these codewords invalid or illegal.
Q. How can errors be detected by using block coding?
If the following two conditions are met, the receiver can detect a change in the original codeword.
The receiver has (or can find) a list of valid codewords.
The original codeword has changed to an invalid one.
The sender creates codewords out of datawords by using a generator that applies the rules and procedures of encoding (discussed later). Each codeword sent to the receiver may change during transmission.
If the received codeword is the same as one of the valid codewords, the word is accepted; the corresponding dataword is extracted for use. If the received codeword is not valid, it is discarded.
However, if the codeword is corrupted during transmission but the received word still matches a valid codeword, the error remains undetected. This type of coding can detect only single errors. Two or more errors may remain undetected.
Examples of block encoding
The 4B/5B block coding is a good example of this type of coding. In this coding scheme, k = 4 and n = 5.
we have 2k = 16 datawords and 2n = 32 codewords.
We saw that 16 out of 32 codewords are used for message transfer and the rest are either used for other purposes or unused.
Q. Let us assume that k = 2 and n = 3. Table below shows the list of datawords and codewords.
Assume the sender encodes the data word 01 as 011 and sends it to the receiver. Consider the following cases:
The receiver receives 011. It is a valid codeword. The receiver extracts the dataword 01 from it.
The codeword is corrupted during transmission, and 111 is received (the leftmost bit is corrupted). This is not a valid codeword and is discarded.
The codeword is corrupted during transmission, and 000 is received (the right two bits are corrupted). This is a valid codeword. The receiver incorrectly extracts the dataword 00. Two corrupted bits have made the error undetectable. An error-detecting code can detect only the types of errors for which it is designed; other types of errors may remain undetected.
| Datawords | Codewords |
|---|---|
| 00 | 000 |
| 01 | 011 |
| 10 | 101 |
| 11 | 110 |
Error Correction
In error detection, the receiver needs to know only that the received codeword is invalid; in error correction the receiver needs to find (or guess) the original codeword sent.
We can say that we need more redundant bits for error correction than for error detection.
Example of Error correction using Block coding
We add 3 redundant bits to the 2-bit dataword to make 5-bit codewords.
Assume the dataword is 01. The sender consults the table (or uses an algorithm) to create the codeword 01011. The codeword is corrupted during transmission, and 01001 is received (error in the second bit from the right).
First, the receiver finds that the received codeword is not in the table. This means an error has occurred. (Detection must come before correction.) The receiver, assuming that there is only 1 bit corrupted, uses the following strategy to guess the correct dataword.
Comparing the received codeword with the first codeword in the table (01001 versus 00000), the receiver decides that the first codeword is not the one that was sent because there are two different bits.
By the same reasoning, the original codeword cannot be the third or fourth one in the table
The original codeword must be the second one in the table because this is the only one that differs from the received codeword by 1 bit. The receiver replaces 01001 with 01011 and consults the table to find the dataword 01.
| Datawords | Codewords |
|---|---|
| 00 | 00000 |
| 01 | 01011 |
| 10 | 10101 |
| 11 | 11110 |