Hamming Distance
The Hamming distance between two words (of the same size) is the number of differences between the corresponding bits. We show the Hamming distance between two words x and y as d(x, y).
The Hamming distance can easily be found if we apply the XOR operation (⊕)on the two words and count the number of 1's in the result. Note that the Hamming distance is a value greater than zero.
Example :The Hamming distance d(000, 011) is 2 because 000 ⊕ 011 is 011 (two 1's)
In a set of words, the minimum Hamming distance is the smallest Hamming distance between all possible pairs. We use dmin to define the minimum Hamming distance in a coding scheme.
When a codeword is corrupted during transmission, the Hamming distance between the sent and received codewords is the number of bits affected by the error. In other words, the Hamming distance between the received codeword and the sent codeword is the number of bits that are corrupted during transmission.
For example , if the codeword 00000 is sent and 01101 is received, 3 bits are in error and the Hamming distance between the two is d(00000, 01101) = 3.
Minimum Distance for Error Detection :
If "s" errors occur during transmission, the Hamming distance between the sent codeword and received codeword is "s". If our code is to detect up to "s" errors, the minimum distance between the valid codes must be "s + 1", so that the received codeword does not match a valid codeword.
In other words, if the minimum distance between all valid codewords is s + 1, the received codeword cannot be erroneously mistaken for another codeword. The distances are not enough (s + 1) for the receiver to accept it as valid. The error will be detected.
This is illustrated below.
Q. The minimum Hamming distance for our first code scheme (Table given below) is 2. This code guarantees detection of only a single error.
For example, if the third codeword (101) is sent and one error occurs, the received codeword does not match any valid codeword.
If two errors occur, however, the received codeword may match a valid codeword and the errors are not detected.
| Datawords | Codewords |
|---|---|
| 00 | 000 |
| 01 | 011 |
| 10 | 101 |
| 11 | 110 |
Q. Our second block code scheme (Table below) has dmin = 3.
This code can detect up to two errors. Again, we see that when any of the valid codewords is sent, two errors create a codeword which is not in the table of valid codewords.
The receiver cannot be fooled. However, some combinations of three errors change a valid codeword to another valid codeword. The receiver accepts the received codeword and the errors are undetected.
| Datawords | Codewords |
|---|---|
| 00 | 00000 |
| 01 | 01011 |
| 10 | 10101 |
| 11 | 11110 |
Q. A code scheme has a Hamming distance dmin = 4. What is the error detection and correction capability of this scheme?
This code guarantees the detection of up to three errors (s = 3), but it can correct up to one error.
In other words, if this code is used for error correction, part of its capability is wasted. Error correction codes need to have an odd minimum distance (3, 5, 7, ... ).
To guarantee correction of up to t errors in an cases, the minimum Hamming distance in a block code must be dmin = 2t + 1.
LINEAR BLOCK CODES
A linear block code is a code in which the exclusive OR (addition modulo-2) of two valid codewords creates another valid codeword.
The scheme in Table above is a linear block code because the result of XORing any codeword with any other codeword is a valid codeword. For example, the XORing of the second and third codewords creates the fourth one.
The scheme in Table above is also a linear block code. We can create all four codewords by XORing two other codewords,
| Datawords | Codewords |
|---|---|
| 00 | 000 |
| 01 | 011 |
| 10 | 101 |
| 11 | 110 |
| Datawords | Codewords |
|---|---|
| 00 | 00000 |
| 01 | 01011 |
| 10 | 10101 |
| 11 | 11110 |
Minimum Distance for Linear Block Codes
It is simple to find the minimum Hamming distance for a linear block code. The minimum Hamming distance is the number of 1s in the nonzero valid code-word with the smallest number of 1's.
In our first code (Table below), the numbers of 1's in the nonzero codewords are 2, 2, and 2. So the minimum Hamming distance is dmin = 2. In our second code (Table below), the numbers of 1's in the nonzero codewords are 3, 3, and 4. So in this code we have dmin = 3
| Datawords | Codewords |
|---|---|
| 00 | 000 |
| 01 | 011 |
| 10 | 101 |
| 11 | 110 |
| Datawords | Codewords |
|---|---|
| 00 | 00000 |
| 01 | 01011 |
| 10 | 10101 |
| 11 | 11110 |
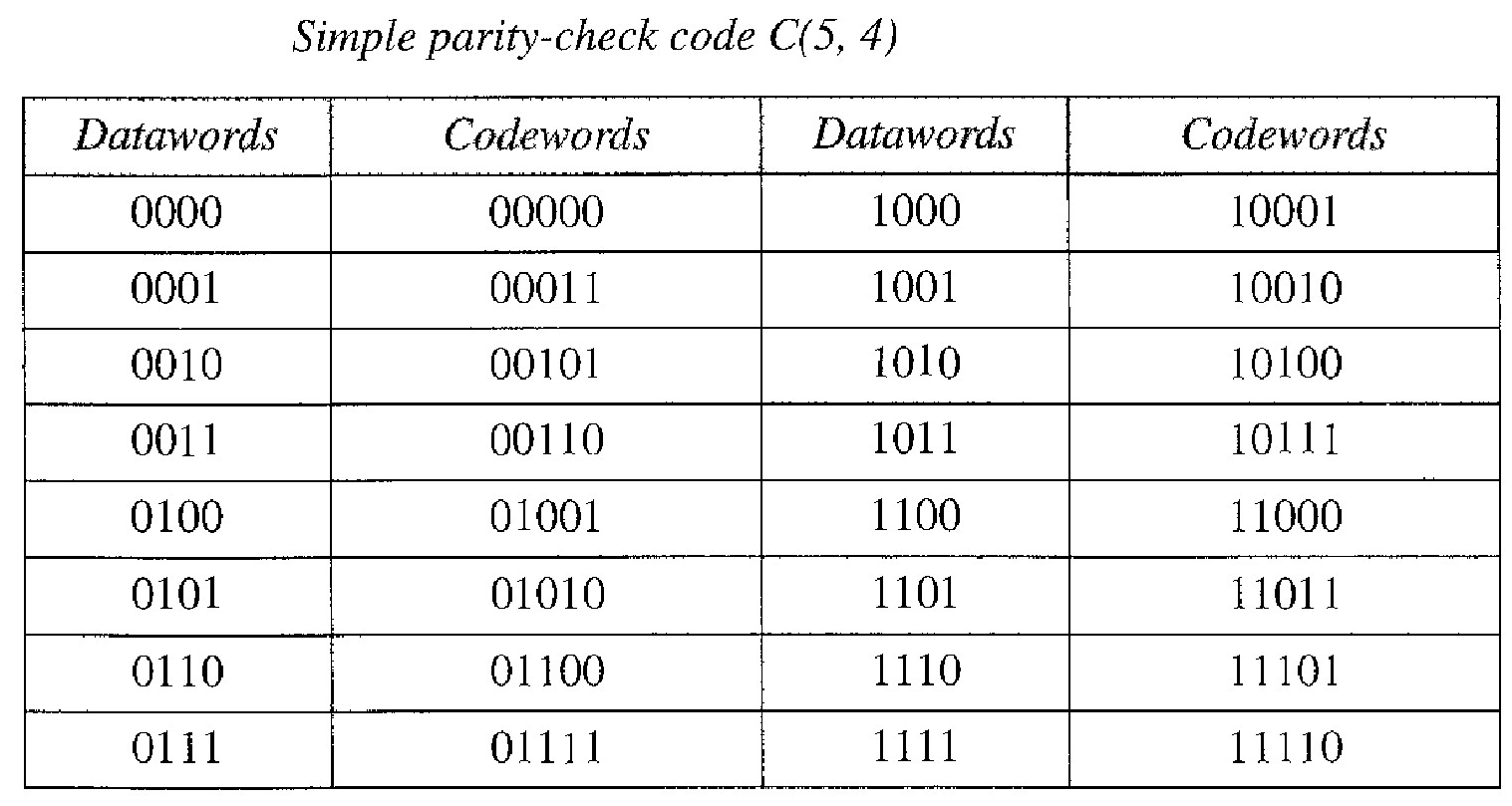
Simple Parity-Check Code
In this code, a k-bit dataword is changed to an n-bit codeword where n = k + 1. The extra bit, called the parity bit, is selected to make the total number of Is in the codeword even.
Although some implementations specify an odd number of 1's, we discuss the even case. The minimum Hamming distance for this category is dmin = 2, which means that the code is a single-bit error-detecting code; it cannot correct any error.
The encoder uses a generator that takes a copy of a 4-bit dataword (a0, a1, a2, a3 ) and generates a parity bit r0. The dataword bits and the parity bit create the 5-bit codeword. The parity bit that is added makes the number of 1's in the codeword even.
This is normally done by adding the 4 bits of the dataword (modulo-2); the result is the parity bit. In other words, r0 = a3 + a2 + a1 + a0 (modulo-2) If the number of Is is even, the result is 0; if the number of Is is odd, the result is 1. In both cases, the total number of 1s in the codeword is even.
The sender sends the codeword which may be corrupted during transmission. The receiver receives a 5-bit word. The checker at the receiver does the same thing as the generator in the sender with one exception: The addition is done over all 5 bits. The result, which is called the syndrome, is just 1 bit. The syndrome is 0 when the number of 1's in the received codeword is even; otherwise, it is 1.
The syndrome is passed to the decision logic analyzer. If the syndrome is 0, there is no error in the received codeword; the data portion of the received codeword is accepted as the dataword; if the syndrome is 1, the data portion of the received codeword is discarded. The dataword is not created.
Scenarios in Transmission
Assume the sender sends the dataword 1011. The codeword created from this dataword is 10111, which is sent to the receiver.
No error occurs; the received codeword is 10111. The syndrome is 0. The dataword 1011 is created
One single-bit error changes A1 The received codeword is 10011. The syndrome is 1. No dataword is created.
One single-bit error changes R0 The received codeword is 10110. The syndrome is 1. No dataword is created. Note that although none of the dataword bits are corrupted, no dataword is created because the code is not sophisticated enough to show the position of the corrupted bit.
An error changes R0 and a second error changes A3 The received codeword is 00110. The syndrome is 0. The dataword 0011 is created at the receiver. Note that here the dataword is wrongly created due to the syndrome value. The simple parity-check decoder cannot detect an even number of errors. The errors cancel each other out and give the syndrome a value of 0.
Three bits A3, A2, A1 are changed by errors. The received codeword is 01011. The syndrome is 1. The dataword is not created. This shows that the simple parity check, guaranteed to detect one single error, can also find any odd number of errors.
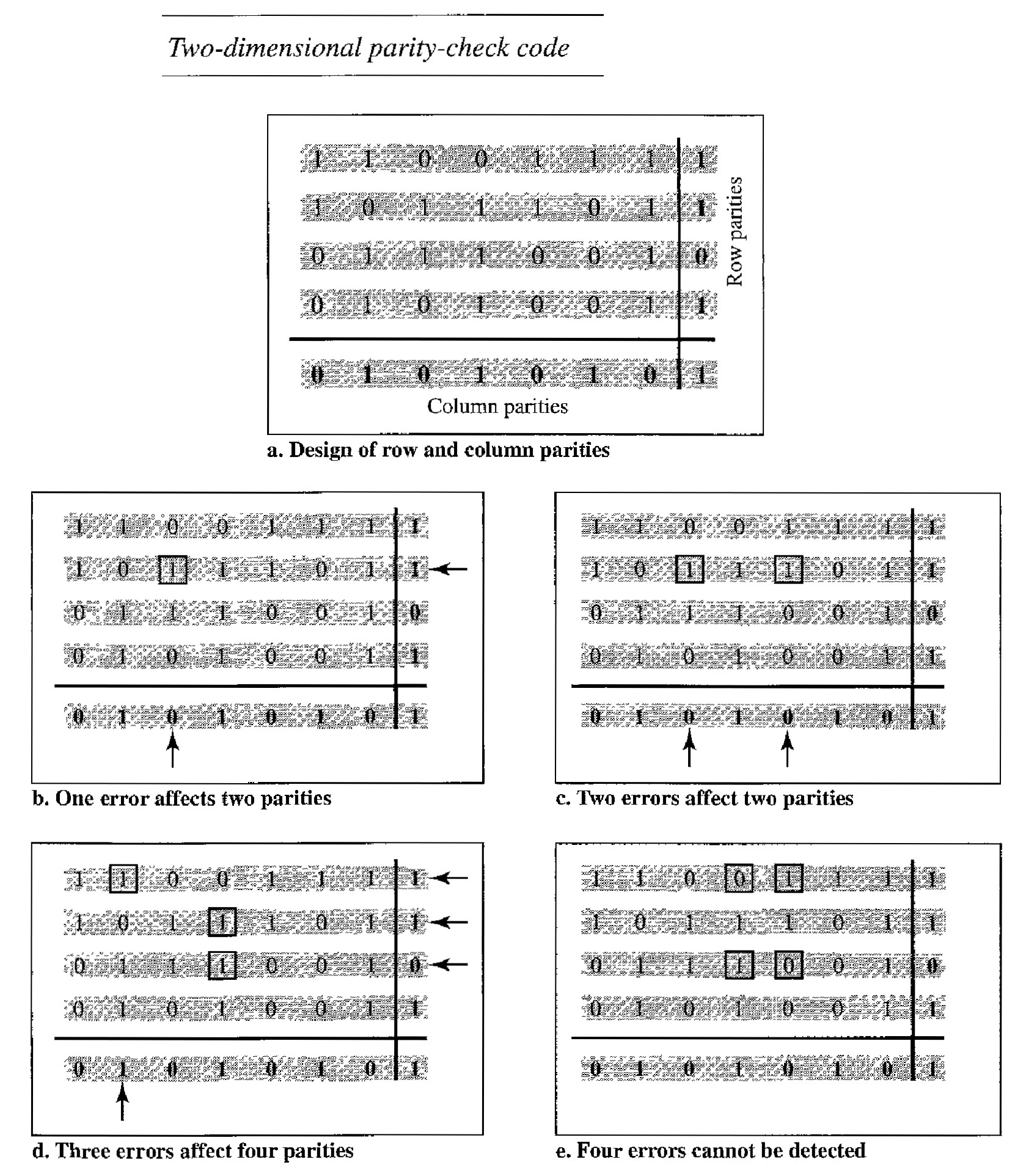
Two-dimensional parity check.
In this method, the dataword is organized in a table (rows and columns).
The data to be sent is five 7-bit bytes, are put in separate rows.
For each row and each column, 1 parity-check bit is calculated. The whole table is then sent to the receiver, which finds the syndrome for each row and each column.
The two-dimensional parity check can detect up to three errors that occur anywhere in the table (arrows point to the locations of the created nonzero syndromes). However, errors affecting 4 bits may not be detected.