GATE-CS-2007
Ans .
A
A function is continuous if for every value of 'x', we have a corresponding f(x). Here, for every x, we have f(x) which is actually the value of x itself, without the negative sign for x < 0. But, the given function is not differentiable for x = 0 because for x < 0, the derivative is negative and for x > 0, the derivative is positive. So, the left hand derivative and right hand derivative do not match. Hence, P is correct and Q is incorrect. Thus, A is the correct option.
Ans .
B
Consider an example set, S = (1,2,3)
Equivalence property follows, reflexive, symmetric and transitive
Largest ordered set are s x s = { (1,1) (1,2) (1,3) (2,1) (2,2) (2,3) (3,1) (3,2) (3,3) } which are 9 which equal to 3^2 = n^2
Smallest ordered set are { (1,1) (2,2) ( 3,3)} which are 3 and equals to n. number of elements.
Ans .
C
No of inputs sequences possible for a n variable Boolean function = \(2^{n}\)
Each input sequence can give either T or F as output ( 2 possible values )
So, Total no of Boolean functions are -
2X2X2X2X2X2X.............X2X2X2X2X2X2
<-------------------- \(2^{n}\) Times -------------->
\(2^{n^{2}}\)
Ans .
C
For a simple, connected, planar graph with v vertices and e edges, the following simple conditions hold: If v = 3 then e = 3v - 6; Note that the question is about non-planar graph G. Only option C doesn't follow above.
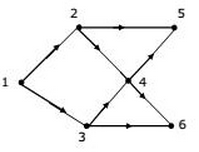
Ans .
D
In option D, 1 appears after 2 and 3 which is not possible in Topological Sorting. In the given DAG it is directly visible that there is an outgoing edge from vertex 1 to vertex 2 and 3 hence 2 and 3 cannot come before vertex 1 so clearly option D is incorrect topological sort. But for questions in which it is not directly visible we should know how to find topological sort of a DAG.
Ans .
B
A set is closed under an operation means when we operate an element of that set with that operator we get an element from that set. Here, CFG generates a CFL and set of all CFLs is the set. But ambiguity is not an operation and hence we can never say that CFG is closed under such operation. Only ambiguity problem for CFGs are undecidable. Thus, option (B) is correct.
Ans .
B
Every finite subset of a non-regular set is regular is True. Each and every set which is finite can have a well-defined DFA for it so whether it is a subset of a regular set or non-regular set it is always regular.
Ans .
C
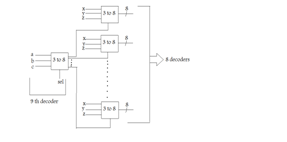
So total signals in=a, b, c, x, y, z i.e. 6 And total output =8*8=64 hence required decoders (from fig.) = 9 so ans is ( C) part.
Ans .
B
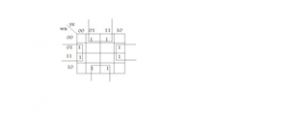
On solving K-MAP we get ZX'+XZ' so it is independent of w,y Ans (B) part.
Question 10
Ans .
D
Here the number of sets = 128/4 = 32 (as it is 4 say set associative)
We have total 64 words then we need 6 bits to identify the word
So the line offset is 5 bits and the word offset is 6 bits
and the TAG = 20-(5+6) =9 bits
so it should be 9,5,6
Ans .
A
Capacity of the disk = 16 surfaces X 128 tracks X 256 sectors X 512 bytes = 256 Mbytes. To calculate number of bits required to access a sector, we need to know total number of sectors.
Total number of sectors = 16 surfaces X 128 tracks X 256 sectors = \(2^{19}\)
So the number of bits required to access a sector is 19.Ans .
C
Maximum number of nodes will be there for a complete tree.
Number of nodes in a complete tree of height h = 1 + 2 + \(2^{2}\) + \(2*3\) +...\(2^{h}\) = \(2^{h+1}-1\)
Ans .
B
O
/ \
O O
(i)
O
/
O
/
O
(ii)
O
/
O
\
O
(iii)
O
\
O
\
O
(iv)
O
\
O
/
O
(v)
The nodes are unlabeled. If the nodes are labeled, we get more number of treesAns .
A
Worst case complexities for the above sorting algorithms are as follows:
Merge Sort — nLogn
Bubble Sort — \(n^{2}\)
Quick Sort — \(n^{2}\)
Selection Sort — \(n^{2}\)
Ans .
D
We can see it by taking few examples like n = 1, n = 3, etc.
For example, for n=5 we have the following (4) comparisons:
------------------------
1 <= 5 (T)
2 <= 5 (T)
4 <= 5 (T)
8 <= 5 (F)
------------------------
CEIL(log_2 n)+2 = CEIL(log_2 5) + 2 = CEIL(2.3) + 2 = 3 + 2 = 5
Ans .
A
Gang scheduling for parallel systems that schedules related threads or processes to run simultaneously on different processors.
Rate monotonic scheduling is used in real-time operating systems with a static-priority scheduling class. The static priorities are assigned on the basis of the cycle duration of the job: the shorter the cycle duration is, the higher is the job’s priority.
Fair Share Scheduling is a scheduling strategy in which the CPU usage is equally distributed among system users or groups, as opposed to equal distribution among processes. It is also known as Guaranteed scheduling.
Ans .
D
Kernel level threads are managed by the OS, therefore, thread operations are implemented in the kernel code. Kernel level threads can also utilize multiprocessor systems by splitting threads on different processors. If one thread blocks it does not cause the entire process to block. Kernel level threads have disadvantages as well. They are slower than user level threads due to the management overhead. Kernel level context switch involves more steps than just saving some registers. Finally, they are not portable because the implementation is operating system dependent.
Ans .
A
Recursive Descent parsing is LL(1) parsing which is top down parsing.
Ans .
A
In Manchester encoding, the bitrate is half of the baud rate.
Ans .
C
UDP is a stateless ,connectionless and unreliable protocol. HTTP needs connection to be established and thus,uses TCP. Telnet is a byte stream protocol which again needs connection establishment ,thus uses TCP. DNS needs request and response ,it needs a protocol in which a server can answer the small queries of large number of users. As UDP is fast and stateless it is the most suitable protocol and thus,it is used in DNS querying . SMTP needs reliability and thus,uses TCP.
Ans .
A
2 can be written as 2 power 2.
Number of partitioning of 2 = no. of non isomorphic
abelian groups
2 can be partitioned as {(2),(1,1)}
Ans .
D
Option A and option C are same G(x)-->C(x) can also be written as ~G(x) or C(x), and they are the correct representation. Option C says :There exists a graph and graph is not connected ,which is equivalent to given sentence. Option D: Every x which is graph is not connected. Option D is correct choice
Ans .
C
A graph has Eulerian Circuit if following conditions are true:a) All vertices with non-zero degree are connected. We don't care about vertices with zero degree because they don't belong to Eulerian Cycle or Path (we only consider all edges).b) All vertices have even degree. Let us analyze all options. A) Any k-regular graph where k is an even number. is not Eulerian as a k regular graph may not be connected (property b is true, but a may not) B) A complete graph on 90 vertices is not Eulerian because all vertices have degree as 89 (property b is false) C) The complement of a cycle on 25 vertices is Eulerian. In a cycle of 25 vertices, all vertices have degree as 2. In complement graph, all vertices would have degree as 22 and graph would be connected.
Ans .
B
All even numbers have the same probability of being first (The odd numbers do not matter here). And there are 10 of them. The probability 2 comes before the other 9 evens is = 1/10. So, option (B) is correct.
Ans .
C
We find the eigenvalues of given matrix by solving its characteristic equation : |(A - (x - 1) I) * (A -(x + 1) I)| = 0 |(A - (x - 1) I)| * |(A - (x + 1) I)| = 0 So, |(A - (x - 1) I)| = 0 or |(A - (x + 1) I)| = 0 Let y be eigenvalues of A, then |(A - y I)| = 0 . So, by comparing equations we get, either x - 1 = y or x + 1 = y Therefore , x = y + 1 or x = y - 1 y = -5, -4, 1, 4 (given) So, x = -4, -1, 2, 5, -6, -3, 0, 3 Thus, option (C) is the answer.
Ans .
C
A partition is said to refine another partition if it splits the sets in the second partition to a larger number of sets.
Ans .
A
To be basis of subspace x, 2 conditions are to be fulfilled 1) They must span x 2) The vectors have to be linearly independent 1)the general solution of x1+x2+x3=0 is \([-x2-x3 , x2 , x3]^{T}\) (Transpose) Which gives two linearly independent solutions by by assuming x2 = 1 and x3 = 0 and next x3 = 1 and x2 = 0 gives \([-1,1,0]^{T}\) and \([-1,0,1]^{T}\) respectively. Since both of these can be generated by linear combinations of \([1,-1,0]^{T}\) & \([-1,0,1]^{T}\) given in question, it span x. 2) Above set of column vector is linearly independent because one cannot be obtained from another by scalar multiplication (second method rank is 2..that is why linearly independent)
Ans .
A
Let us try to convert in Newton Rapson's form by putting Xn as
first part.
\(X_{n+1}\) = \(X_{n}\) - \(X_{n}\)/2 + 9/(8 \(X_{n}\))
So f(X) = (4*\(X_{n}^2\) - 9)
and f'(X) = 8*\(X_{n}\)
So clearly f(X) = 4\(X^{2}\) - 9. If we start from \(X^{0}\) = 0.5, according to equation, we cannot get negative value at any time, so answer is 1.5 i.e. option (A) is correct.
Ans .
A
Here a string w of 0's and 1's should have the property that, the no of 0's in the string w should be divisible by 3 ( N(0) % 3 =0 ), and the number of 1's the string w should be divisible by 5 (N(1) % 5 =0). Having said that, the Language will contain the strings such as : { e , 000, 11111, 00011111, 00111101 , 11111000, 10101011 , 00000011111,....and so on } So, strings accepted by the automaton have to be of length 0, 3, 5, 8, 11, 13, 14, 16....and so on, i.e. equation for length will be 3x + 5y (where x,y>=0 ) Modulo 3 gives remainder as ( 0, 1, 2 ) , and Modulo 5 gives remainder as ( 0, 1, 2, 3, 4 ). Hence 3 * 5 sates, i.e. there will be 15 states in the automaton to represent this.
Ans .
B
Let us first design a deterministic pushdown automata for the given language.
For each occurrence of '0' , we PUSH X in the stack.
When '2' appears, no stack operation is performed. But, state of the automata is changed.
For each occurrence of '1' , we POP X from the stack.
If at the end Z0 is on the stack top then input string is accepted
We also design a Turing machine for the given language.
When '0' appears in the input string , we replace it with X .Then, traverse to the rightmost corner and replace '1' with Y.
We go back to the leftmost '0' and repeat the above process.
While traversing rightwards from the beginning of the input string, if after X, '2' appears and after '2', Y appears then we reach the HALT state. Thus, the given language is recursive. Every recursive language is a CFL. Thus, option (B) is the answer.
Ans .
C
(C) Strings which are the part of this language are either 0w0 or 1w1 where w is any string in {0, 1}* . Thus, language given in option (C) is regular.
All other languages accept strings which have a palindrome as their substring.
(A) Strings intersect with 0*110* .
(B) Strings intersect with 0*110*1 .
(D) Strings intersect with 10*110* .
According to pumping lemma, languages given option (A), (B) and (D) are irregular.
Thus, option (C) is the answer.
Ans .
D
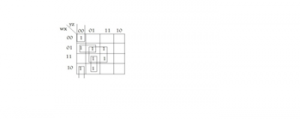
Solving this k-map we get x'y'z' + w'xy' + wy'z + xz which is (A) part
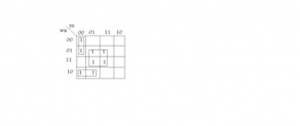
Solving this k-map we get w'y'z' + wx'y' + xz which is (B) part.
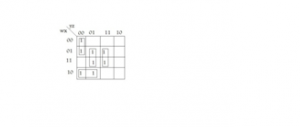
Solving this k-map we get w'y'z' + wx'y' + xyz + xy'z which is ( C) part . But we can't get (D) part from any combination so Ans is (D) part.
Ans .
D
* is nothing but working as EX NOR here.Explanation: P: X= Y * Z =(Y XOR Z) =YZ + Y'Z' =Y(XY + X'Y')+Y'(XY+X'Y')' =XY+Y'((Y XOR X)')' =XY+Y'(Y XOR X) =XY+Y'(Y'X+X'Y) =XY+Y'X =X(Y+Y') =X Q: Y=X*Z =(X XOR Z)' =X(XY + X'Y') + X'(XY + X'Y')' =XY+X'(X'Y+XY') =XY+X'Y =Y R: X * Y *Z WE HAVE SEEN FROM P Y*Z =X SO X * X NOT(X XOR X)=X'X'+XX SO ALL P,Q,R ARE CORRECT ANS IS (D)
Ans .
C
We can use n-1 selection lines , and using 0,1 and nth variable and its compliment to realize the function So ans is \(2^{(n-1)}\):1 Part-(C )
Ans .
B
let the carry input be c0 Now, c1 = g0 + p0c0 = 1 AND, 1 OR c2 = g1 + p1g0 + p1p0c0 = 2 AND, 1 OR c3 = g2 + p2g1 + p2p1go + p2p1p0c0 = 3 AND, 1 OR c4 = g3 + p3g2 + p3p2g1 + p3p2p1g0 + p3p2p1p0c0 = 4 AND, 1 OR So, total AND gates = 1+2+3+4 = 10 , OR gates = 1+1+1+1 = 4 So as a general formula we can observe that we need a total of " n(n+1)/2 " AND gates and "n" OR gates for a n-bit carry look ahead circuit used for addition of two binary numbers.
Ans .
C
Ans .
C
1 2 3 4 5 6 7 8 R2!R1!R0 IF ID EX WB R4!R3!R2 IF ID EX EX EX WB R6!R5!R4 IF ID - - EX WBThis is the table shows the cycle phases and number of cycles require for given instruction. No. of cycles required=8 So (B) is correct option.
Ans .
A
1. While there are input tokens left
o Read the next token from input.
o If the token is a value
+ Push it onto the stack.
o Otherwise, the token is an operator
(operator here includes both operators, and functions).
* It is known a priori that the operator takes n arguments.
* If there are fewer than n values on the stack
(Error) The user has not input sufficient values in the expression.
* Else, Pop the top n values from the stack.
* Evaluate the operator, with the values as arguments.
* Push the returned results, if any, back onto the stack.
2. If there is only one value in the stack
o That value is the result of the calculation.
3. If there are more values in the stack
o (Error) The user input has too many values.
First three tokens are values, so they are simply pushed. After pushing 8, 2 and 3, the stack is as follows8, 2, 3
When ^ is read, top two are popped and power(2^3) is calculated
8, 8
When / is read, top two are popped and division(8/8) is performed
1
Next two tokens are values, so they are simply pushed. After pushing 2 and 3, the stack is as follows
1, 2, 3
When * comes, top two are popped and multiplication is performed.
1, 6
Ans .
A
Below is the given tree.
a
/ \
/ \
b c
/ \ / \
/ \ / \
d e f g
Ans .
B
- - - - - - -
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 1 is 0, so let us put the value at 0
1 - - - - - -
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 3 is 6, so let us put the value at 6
1 - - - - - 3
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 8 is 0, but 0 is already occupied, let us put the value(8) at next available space(1)
1 8 - - - - 3
0 1 2 3 4 5 6
The value of function (3x + 4)mod 7 for 10 is 6, but 6 is already occupied, let us put the value(10) at next available space(2)
1 8 10 - - - 3
0 1 2 3 4 5 6
Ans .
D
* Time Comlexity of the Dijkstra's algorithm is O(\(|V|^{2}\) + E)
* Time Comlexity of the Warshall's algorithm is O(\(|V|^{3}\))
* DFS cannot be used for finding shortest paths
* BFS can be used for unweighted graphs. Time Complexity for BFS is O(|E| + |V|)
Ans .
D
f(5) = f(3)+2
The line "r = n" changes value of r to 5. Since r
is static, its value is shared be all subsequence
calls. Also, all subsequent calls don't change r
because the statement "r = n" is in a if condition
with n > 3.
f(3) = f(2)+5
f(2) = f(1)+5
f(1) = f(0)+5
f(0) = 1
So f(5) = 1+5+5+5+2 = 18
Ans .
C
For an n-ary tree where each node has n children or no children, following relation holds
L = (n-1)*I + 1
Where L is the number of leaf nodes and I is the number of internal nodes.
Let us find out the value of n for the given data.
L = 41 , I = 10
41 = 10*(n-1) + 1
(n-1) = 4
n = 5
Ans .
A
Above code is implementation of the Euclidean algorithm for finding Greatest Common Divisor (GCD).
Ans .
D
Recursive relation for the DoSomething() is
T(n) = T(\(\sqrt{n}\)) + C1 if n > 2
We have ignored the floor() part as it doesn't matter here if it's a floor or ceiling.
Let n = 2^m, T(n) = T(2^m)
Let T(2^m) = S(m)
From the above two, T(n) = S(m)
S(m) = S(m/2) + C1 /* This is simply binary search recursion*/
S(m) = O(logm)
= O(loglogn) /* Since n = 2^m */
Now, let us go back to the original recursive function T(n)
T(n) = S(m)
= O(LogLogn)
Ans .
C
The value returned by GetValue() when a pointer to the root of a binary tree is passed as its argument is: (A) the number of nodes in the tree (B) the number of internal nodes in the tree (C) the number of leaf nodes in the tree (D) the height of the tree Answer (C)
Ans .
B
The height of a Max Heap is \(\theta\)(logn). If we perform binary search for finding the correct position then we need to do \(\theta\)(LogLogn) comparisons.
Ans .
A
We can easily prove that for any formula, there is a truth assignment for which at least half the clauses evaluate to true . Proof : Consider an arbitrary truth assignment. For each of its clause 'j' , introduce a random variable. \(X_{j}\) = 1 if clause 'j' is satisfied \(X_{j}\) = 0 otherwise Then, X = summation of (j * \(X_{j}\)) is the number of satisfied clauses. Given any clause 'c' , it is unsatisfied only if all of its 'k' constituent literals evaluates to false as they are joined by OR operator. Now, because each literal within a clause has a 1/2 chance of evaluating to true independently of any of the truth value of any of the other literals, the probability that they are all false is \((1 / 2)^{k}\) . Thus, the probability that 'c' is satisfied = 1 - \((1 / 2)^{k}\) So, E(\(X_{j}\)) = 1 * \((1 / 2)^{k}\) = \((1 / 2)^{k}\) Therefore, E(\(X_{j}\)) >= 1/2 Summation on both sides to get E(X). Therefore, we have E(X) = summation of (j * \(X_{j}\)) >= m/2 where 'm' is the number of clauses. E(X) represents expected number of satisfied clauses. Thus, there must exist an assignment that satisfies at least half of the clauses.
Ans .
D
(A), (B) and (C) are correct.
(D) is incorrect as there may be many edges of wight w in the graph and e may not be picked up in some of the minimum spanning trees.
Ans .
B
Total number of comparisons: let number of comparisons be T(n). T(n) can be written as follows: Algorithmic Paradigm: Divide and Conquer
T(n) = T(floor(n/2)) + T(ceil(n/2)) + 2 T(2) = 1 T(1) = 0If n is a power of 2, then we can write T(n) as:
T(n) = 2T(n/2) + 2After solving above recursion, we get
T(n) = 3/2n -2Thus, the approach does 3/2n -2 comparisons if n is a power of 2. And it does more than 3/2n -2 comparisons if n is not a power of 2.
Ans .
B
Big O notation describes the upper bound and Big Omega notation describes the lower bound for an algorithm.
The for loop in the question is run maximum sqrt(n) times and minimum 1 time. Therefore, T(n) = O(sqrt(n)) and T(n) = \(\Omega\)(1)
Ans .
C
A LL(1) grammar doesn't give to multiple entries in a single cell of its parsing table. It has only single entry in a single cell, hence it should be unambiguous.
Option A is wrong. Grammar is not left recursive. For a grammar to be left recursive a production should be of form A->Ab, where A is a single Non-Terminal and b is any string of grammar symbols.
Option B is wrong. Because a right recursive grammar has nothing to do with LL(1).
Option D is wrong. Because the given grammar is clearly a Context Free Grammar. A grammar is CFG if it has productions of the form A->(V U T)* , where A is a single non-terminal and V is a set of Non-terminals and T is a set of Terminals.
Ans .
C
A regular grammar can also be ambiguous also
For example, consider the following grammar,
S -> aA/a
A -> aA/\(\epsilon\)
In above grammar, string 'a' has two leftmost
derivations.
(1) S -> aA (2) S -> a
S->a (using A->\(\epsilon\))
And LL(1) parses only unambiguous grammar,
so statement P is False.
Statement Q is true is for every regular set, we can have a regular
grammar which is unambiguous so it can be parse by LR parser.
So option C is correct choice
Ans .
B
For Instructions of t2 and t3 1. MOV c, t2 2. OP d, t2(OP=ADD) 3. OP e, t2(OP=SUB) For Instructions of t1 and t4 4. MOV a, t1 5. OP b, t1(OP=ADD) 6. OP t1, t2(OP=SUB) 7. MOV t2, a(AS END Value has To be in the MEMORY) Step 6 should have been enough, if the question hadn't asked for final value in memory and rather be in register. The final step require another MOV, thus a total of 3.
Ans .
B
Shortest remaining time, also known as shortest remaining time first (SRTF), is a scheduling method that is a pre-emptive version of shortest job next scheduling. In this scheduling algorithm, the process with the smallest amount of time remaining until completion is selected to execute. Since the currently executing process is the one with the shortest amount of time remaining by definition, and since that time should only reduce as execution progresses, processes will always run until they complete or a new process is added that requires a smaller amount of time. The Gantt chart of execution of processes:

At time 0, P1 is the only process, P1 runs for 15 time units. At time 15, P2 arrives, but P1 has the shortest remaining time. So P1 continues for 5 more time units. At time 20, P2 is the only process. So it runs for 10 time units. at time 30, P3 is the shortest remaining time process. So it runs for 10 time units. at time 40, P2 runs as it is the only process. P2 runs for 5 time units. At time 45, P3 arrives, but P2 has the shortest remaining time. So P2 continues for 10 more time units. P2 completes its execution at time 55.
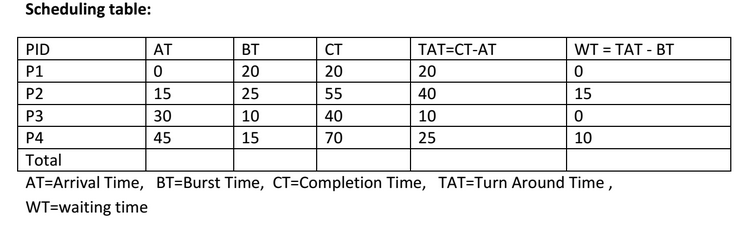
As we know, turn around time is total time between submission of the process and its completion. Waiting time is the time The amount of time that is taken by a process in ready queue and waiting time is the difference between Turn around time and burst time. Total turnaround time for P2 = Completion time - Arrival time = 55 - 15 = 40 Total Waiting Time for P2= turn around time - Burst time = 40 – 25 = 15
Ans .
B
First In First Out Page Replacement Algorithms: This is the simplest page replacement algorithm. In this algorithm, operating system keeps track of all pages in the memory in a queue, oldest page is in the front of the queue. When a page needs to be replaced page in the front of the queue is selected for removal. FIFO Page replacement algorithms suffers from Belady's anomaly : Belady's anomaly states that it is possible to have more page faults when increasing the number of page frames. Solution: Statement P: Increasing the number of page frames allocated to a process sometimes increases the page fault rate. Correct, as FIFO page replacement algorithm suffers from belady's anomaly which states above statement. Statement Q: Some programs do not exhibit locality of reference. Correct, Locality often occurs because code contains loops that tend to reference arrays or other data structures by indices. So we can write a program does not contain loop and do not exhibit locality of reference. So, both statement P and Q are correct but Q is not the reason for P as Belady's Anomaly occurs for some specific patterns of page references.
Ans .
C
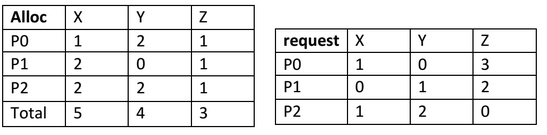
A single processor system has three resource types X, Y and Z, which are shared by three processes. There are 5 units of each resource type. So, the resource instances which are left being unallocated = <0,1,2> { unallocated resources= total resources-allocated resources } nitika_57 now, from the request table, you can say that only request of P1 can be satisfied. So P1 can finish its execution first. Once P1 is done, it releases 2, 0 and 1 units of X, Y and Z respectively which were allocated to P1.So, Now unallocated resource instance are = <0,1,2> +<2,0,1> = <2,1,3> Now Among P0 and P2, needs of P0 can only be satisfied. So P0 finishes its execution. Once P2 is done, It releases 2,2,and 1 units of X,Y and Z respectively which were allocated to P2.SO, Now unallocated resource instance are= <2,1,3> + <2,2,1> = <4,3,4>. Finally, P2 finishes its execution. So, P2 is the process which finishes in end. Option (C) is the correct answer.
Ans .
D
Bounded waiting :There exists a bound, or limit, on the number of times other processes are allowed to enter their critical sections after a process has made request to enter its critical section and before that request is granted. mutual exclusion prevents simultaneous access to a shared resource. This concept is used in concurrent programming with a critical section, a piece of code in which processes or threads access a shared resource. Solution: Two processes, P1 and P2, need to access a critical section of code. Here, wants1 and wants2 are shared variables, which are initialized to false. Now, when both wants1 and wants2 become true, both process p1 and p2 enter in while loop and waiting for each other to finish. This while loop run indefinitely which leads to deadlock. Now, Assume P1 is in critical section (it means wants1=true, wants2 can be anything, true or false). So this ensures that p2 won't enter in critical section and vice versa
Ans .
B
The expression given in question does following steps in sequence. a) Select studids of all female students and selects all courseids of all courses. b) Then the query does a Cartesian Product of the above select two columns from different tables. c) Finally it subtracts enroll table from the result of above step (b). This will remove all the (studid, courseid) pairs which are present in enroll table. If all female students have registered in a courses, then this course will not be there in the subtracted result. So the complete expression returns courses in which a proper subset of female students are enrolled.
studinfo table studid name sex ------------------------ 1 a Male 2 c Female 3 d Female enroll table studid courseid ------------------ 1 1 2 1 3 1 2 2 3 3 3 2 Result of step b studid courseid --------------------- 2 1 2 2 2 3 3 1 3 2 3 3 Result of step c studid courseid ------------------- 2 3
Ans .
C
The query selects all those employees whose immediate subordinate is "male". In other words, it selects names of employees with no immediate female subordinates
Ans .
A
First note that they asked for Anyone (= All) not for Any. Here, Everyone means all of the group. Anyone means all or any part of the group. Let the employee(empId, name, department, salary) have the following instance. empId name department salary -------
e1 ------- A-------- 1---------10000 e2 -------B ------- 5 ---------5000 e3 -------C ------- 5----------7000 e4 -------D ------- 2----------2000 e5 -------E ------- 3----------6000Now the actual result should contain empId : e1 , e3 and e5 ( because they have salary greater than anyone employee in the department '5') ------- Now Q1 : Note : EXISTS(empty set) gives FALSE, and NOT EXISTS(empty set) gives TRUE.
Select e.empId From employee e Where not exists (Select * From employee s where s.department = "5" and s.salary >=e.salary)Q1 will result only empId e1. ----------- whereas Q2 :
Select e.empId From employee e Where e.salary > Any (Select distinct salary From employee s Where s.department = "5")Q2 will result empId e1, e3 and e5. ------------ Hence Q1 is the correct query. Note that if we use ALL in place of Any in second query then this will be correct. Option (A) is correct.
Ans .
D
First note that they asked for Anyone (= All) not for Any. Here, Everyone means all of the group. Anyone means all or any part of the group. Let the employee(empId, name, department, salary) have the following instance. empId name department salary -------
If a relational schema is in BCNF then all redundancy based on functional dependency has been removed, although other types of redundancy may still exist. A relational schema R is in BCNF form if and only if for every one of its dependencies X -> Y, at least one of the following conditions hold : 1. X -> Y is a trivial functional dependency i.e. Y is a subset of X . 2. X is a super key for schema R So, we check transitive dependency for only non-prime attributes in case of BCNF. Thus, the statement 'A prime attribute can be transitively dependent on a key in a BCNF relation' is false. Thus, option (D) is the answer.
Ans .
A
Disk Block size = 1024 bytes Data Record Pointer size, r = 7 bytes Value size, V = 9 bytes Disk Block ptr, P = 6 bytesLet order of leaf be m. A leaf node in B+ tree contains at most m record pointers, at most m values, and one disk block pointer. r*m + V*m + p <= 1024 16m <= 1018 m =< 63
Ans .
C
S1 is not conflict serializable, but S2 is conflict serializable
Schedule S1
T1 T2
---------------------
r1(X)
r1(Y)
r2(X)
r2(Y)
w2(Y)
w1(X)
The schedule is neither conflict equivalent to T1T2, nor T2T1.
Schedule S2
T1 T2
---------------------
r1(X)
r2(X)
r2(Y)
w2(Y)
r1(Y)
w1(X)
The schedule is conflict equivalent to T2T1.
Ans .
B
P(X) = Probability that station X attempts to transmit = P P (-X) = Probability that station X does not transmit = 1-P Required is: Probability that only one station transmits = y
Y = (A1, -A2, -A3...-An) + (-A1, A2, A3...-An) + (-A1, -A2, A3.....-An) + .... + (-A1, -A2, -A3......An) = (p*(1-p)*(1-p)*.... (1-p) + (1-p)*p*(1-p)...(1-p) + ..... = p*\((1-p)^{(n-1)}\) + p*\((1-p)^{n-1}\) + .. + p*(1-p)^(n-1) = n*p*\((1-p)^{(n-1)}\)
Ans .
C
Transmission delay for 1 bit t = 1/\((10^{7}\)) = 0.1 micro seconds. 200 meters can be traveled in 1 micro second. Therefore, in 0.1 micro seconds, 20 meters can be traveled.
Ans .
C
Maximum number of subnets = 2^6-2 =62. Note that 2 is subtracted from 2^6. The RFC 950 specification reserves the subnet values consisting of all zeros (see above) and all ones (broadcast), reducing the number of available subnets by two. Maximum number of hosts is 2^10-2 = 1022. 2 is subtracted for Number of hosts is also. The address with all bits as 1 is reserved as broadcast address and address with all host id bits as 0 is used as network address of subnet. In general, the number of addresses usable for addressing specific hosts in each network is always 2^N - 2 where N is the number of bits for host id.
Ans .
B
11001001 000 <--- input right padded by 3 bits
1001 <--- divisor
01011001 000 <---- XOR of the above 2
1001 <--- divisor
00010001 000
1001
00000011 000
10 01
00000001 010
1 001
00000000 011 <------- remainder (3 bits)
After dividing the given message 11001001 by 1001, we get the remainder as 011 which is the CRC. The transmitted data is, message + CRC which is 11001001 011.
Ans .
C
Distance between stations = L KM
Propogation delay per KM = t seconds
Total propagation delay = Lt seconds
Frame size = k bits
Channel capacity = R bits/second
Transmission Time = k/R
Let n be the window size.
UtiliZation = n/(1+2a) where a = Propagation time / transmission time
= n/[1 + 2LtR/k]
= nk/(2LtR+k)
For maximum utilization: nk = 2LtR + k
Therefore, n = (2LtR+k)/k
Number of bits needed for n frames is Logn.
Ans .
B
SMTP is an application layer protocol used for e-mail transmission.
TCP is a core transport layer protocol.
BGP is a network layer protocol backing the core routing decisions on the Internet
PPP is a data link layer protocol commonly used in establishing a direct connection between two networking nodes.
Ans .
D
Ist memory reference R1 <- M[3000] and then in the loop which runs for 10 times, because the content of memory location 3000 is 10 given in question and loop will run 10 times as R2 <- M[R3] M[R3] <-R2 There are two memory reference every iteration 10*2=20 Total=20+1=21 So (D) is correct option.
Ans .
D
Program stores results from 2000 to 2010. It stores 110,109,108...100 at 2010 location. So at 2010 it stores 100 Because DEC R1 is instruction which decrements register value by 1. So (A) is correct option.
Ans .
C
If memory is byte addressable so for each instruction it requires 1 word that is equal to 4 bytes which require 4 addresses
Instruction Word location MOV R1,3000 2 1000-1007 MOV R2,R1 1 1008-1011 ADD R2,R1 1 1012-1015 MOV(R3),R2 1 1016-1019 INC R3 1 1020-1023 DEC R1 1 1024-1027Interrupt occur during execution of instruction INC R3. So CPU will complete the execution of this instruction and push the next address 1024 in the stack. So after interrupt service program can be resumed for next instruction. So (C) is correct option.
Ans .
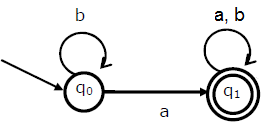
C
In this case, we would at least have to reach q1 so that our string gets accepted. So, b* a is the smallest accepted string. Now, at q1, any string with any number of a's and b's would be accepted. So, we append (a + b)* to the smallest accepted string.
Thus, the string accepted by the FSA is b* a (a + b)*.
Thus, C is the correct choice.
Ans .
B
Following is equivalent FSA with 2 states.
Ans .
A
We get the following Huffman Tree after applying Huffman Coding Algorithm. The idea is to keep the least probable characters as low as possible by picking them first. The letters a, b, c, d, e, f have probabilities 1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively.
1
/ \
/ \
1/2 a(1/2)
/ \
/ \
1/4 b(1/4)
/ \
/ \
1/8 c(1/8)
/ \
/ \
1/16 d(1/16)
/ \
e f
Ans .
D
We get the following Huffman Tree after applying Huffman Coding Algorithm. The idea is to keep the least probable characters as low as possible by picking them first. The letters a, b, c, d, e, f have probabilities 1/2, 1/4, 1/8, 1/16, 1/32, 1/32 respectively.
1
/ \
/ \
1/2 a(1/2)
/ \
/ \
1/4 b(1/4)
/ \
/ \
1/8 c(1/8)
/ \
/ \
1/16 d(1/16)
/ \
e f
The average length = (1*1/2 + 2*1/4 + 3*1/8 + 4*1/16 + 5*1/32 + 5*1/32)
= 1.9375
Ans .
C
Given below production rules.
S --> aB S --> bA B --> b A --> a B --> bS A --> aS B --> aBB A --> bAAWe can derive aabbab using below sequence
S -> aB [Using S --> aB] -> aaBB [Using B --> aBB] -> aabB [Using B --> b] -> aabbS [Using B --> bS] -> aabbaB [Using S --> aB] -> aabbab [Using B --> b]
Ans .
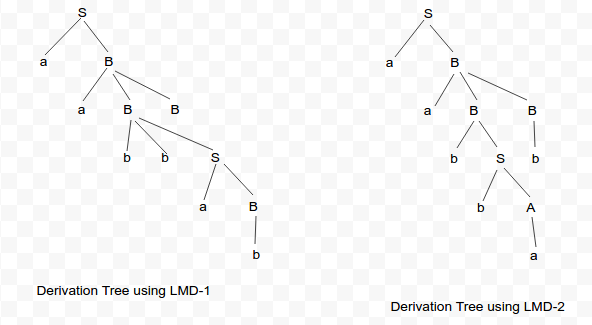
B
When it asks about the no of derivations tree, we should consider either left most derivation(LMD) or right most derivations(RMD), but not both. Here two left most derivations are possible for the correct string of the previous question "aabbab" from the given grammar. LMD-1 S -> aB [Using S --> aB] -> aaBB [Using B --> aBB] -> aabB [Using B --> b] -> aabbS [Using B --> bS] -> aabbaB [Using S --> aB] -> aabbab [Using B --> b] LMD-2 S -> aB [Using S --> aB] -> aaBB [Using B --> aBB] -> aabSB [Using B --> bS] -> aabbAB [Using S --> bA] -> aabbaB [Using A --> a] -> aabbab [Using B --> b] The Derivation tress are shown below :
Ans .
C
Size of main memory=\(2^{16}\) bytes Size of cache=32*64 Bytes =\(2^{11}\) Bytes Size of array=2500 Bytes Array is stored in main memory but cache will be empty Size of cache=2048 Bytes So number of page faults=2500-2048=452 Complete array will be access twice So for second access no. of total page faults=452*2=904 So total page faults=452+904=1356 So data cache misses will be 56 So (C) is correct option
Ans .
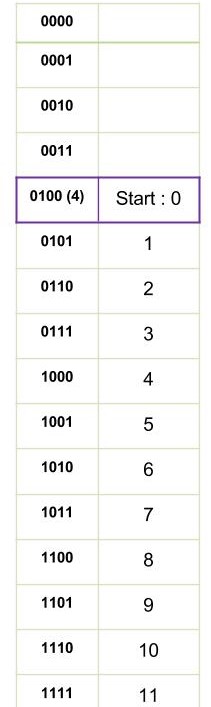
A
Size of Main Memory = 2^16 bytes No. of lines = 32 = 2^5 Size of each line = 64 = 2^6 bytes => Word Offset = 6 2 way set is present Hence, No.of sets = No. of lines / 2 = 2^5 / 2 = 2^4 Now, Main memory format= ////// Sir 1st image here.
Starting memory location : 1100 H => 0001 0001 0000 0000 Offset : 00 0000 Line : 01 00 (4)

Ans .
A
Optimal replacement policy looks forward in time to see which frame to replace on a page fault. 1 23 -> 1,2,3 //page faults 173 ->7 143 ->4 153 -> 5 163 -> 6 Total=7 So Answer is A
Ans .
C
LRU replacement policy: The page that is least recently used is being Replaced. Given String: 1, 2, 1, 3, 7, 4, 5, 6, 3, 1 123 // 1 ,2, 3 //page faults 173 ->7 473 ->4 453 ->5 456 ->6 356 ->3 316 ->1 Total 9 In http://geeksquiz.com/gate-gate-cs-2007-question-82/, In optimal Replacement total page faults=7 Therefore 2 more page faults Answer is C
Ans .
A
At each move, robot can move either 1 unit right, or 1 unit up, and there will be 20 such moves required to reach (10,10) from (0,0). So we have to divide these 20 moves, numbered from 1 to 20, into 2 groups: right group and up group. Right group contains those moves in which we move right, and up group contains those moves in which we move up. Each group contains 10 elements each. So basically, we have to divide 20 things into 2 groups of 10 10 things each, i.e., we need to find all possible arrangements of {r, r, r, r, r, r, r, r, r, r, u, u, u, u, u, u, u, u, u, u} where r represents right move and u represents up move. The arrangements can can be done in 20! / (10!*10!) = 20C10 ways. So option (A) is correct.