NCERT Class 11 Chapter-1: Sets
Practise Exercise-1.1
Q.1: Which of the following are sets. Explain your answer.
(a). The collection of all day in a week which have the first letter S.
Answer : Based on the formulae given in Sets:
In a year we can easily identify all the days in a week which starts with the letter S. So it will form a clearly defined collection of objects.
Hence, the given collection can be a set.
(b). The collection of ten most famous singers of India.
Answer: Based on the formulae given in Sets
If we talk about the most famous singers then it is not a well-defined collection, because there are different parameters to be famous. So, it does not fall in this category.
Hence, the given collection cannot be a set.
(c). A group of best football strikers of the world.
Answer: Based on the formulae given in Sets
A group of best football strikers cannot be determined because each individual have different point of view to identify the best football strikers. So it does not form a well-defined collection.
Hence, this group is not a set.
(d). The collection of all girls in your school.
Answer:
The collection of all girls in your school can easily be identified as this category is clearly defined.
Hence, the given collection can be a set.
(e). The collection of all odd numbers below 50.
Answer: Based on the formulae given in Sets
The collection of all odd numbers below 50 can be identified by calculating, so it forms a well-defined collection. .
Hence, the given collection can be a set.
(f). A collection of poems written by the poet Shakespeare.
Answer: Based on the formulae given in Sets
A collection of all the poems written by Shakespeare can be identified easily as he has the copyright on all his poems. So it forms a well-defined collection.
Hence the given collection can be a set.
(g). The collection of all prime numbers.
Answer: Based on the formulae given in Sets
All prime numbers can be identified after doing some calculations and thus it forms a well-defined collection.
Hence, the given collection can be a set.
(h). The collection of questions in science book.
Answer: Based on the formulae given in Sets
We can find out the given question in a science book, so it will form a well-defined collection of objects.
Hence, the given collection can be a set.
(i). A collection of most dangerous reptiles in India.
Answer: Based on the formulae given in Sets
If we are talking about the most dangerous reptiles in India, and then it would be difficult to tell. This category will vary from person to person. So it does not fall in the category of well-defined collection.
Hence, the given collection cannot be a set.
Q.2: Let P = {2, 3, 4, 5, 6, 7}. Insert the correct symbol \(\in\:or\:\notin\) inside the given blank spaces below:
(a). 2 . . . . . . . . . . P
(b). 9 . . . . . . . . . P
(c). 11 . . . . . . . . P
(d). 4 . . . . . . . . P
(e). 0 . . . . . . . . P
(f). 7 . . . . . . . . P
Answer: Based on the formulae given in Sets
(a). \(2\in\:P\)
(b). \(9\notin\:P\)
(c). \(11\notin\:P\)
(d). \(4\in\:P\)
(e). \(0\notin\:P\)
(f). \(7\in\:P\)
Q.3: Write the given sets in roster form:
(a). P = {y: y is an integer and -4 < y < 6}.
(b). Q = {y: y is a natural number which is <8}
(c). R = {y: y is a 2 digit natural number in which the sum of its digits is 9}
(d). S = {y: y is a prime number which is a divisor of 70}
(e). T = The set of all letters in the word ELEPHANT
(f). U = The set of all letters in the word DIVISION
Answer: Based on the formulae given in Sets
(a). P = {y: y is an integer and -4 < y < 6}
The elements from this given set are –3, –2,-1, 0, 1, 2, 3, 4, and 5 only.
Hence, we can write the following set in the roaster form as given below:
P = {–3, –2,-1, 0, 1, 2, 3, 4, 5}
(b). Q = {y: y is a natural number which is <6}
The elements from this given set are 1, 2, 3, 4, 5, 6, and 7 only.
Hence, we can write the following set in the roaster form as given below:
Q = {1, 2, 3, 4, 5, 6, 7}
(c). R = {y: y is a 2 digit natural number in which the sum of its digits is 9}
The elements from this given set are 18, 27, 36, 45, 54, 63, 72, 81 and 90 only.
Hence, we can write the following set in the roaster form as given below:
R = {18, 27, 36, 45, 54, 63, 72, 81, 90}
(d). S = {y: y is a prime number which is a divisor of 140}
70 = 2 x 2 x 5 x 7
The elements from this given set are 2, 5, and 7 only.
Hence, we can write the following set in the roaster form as given below:
S = {2, 5, 7}.
(e). T = The set of all letters in the word ELEPHANT
There are 8 letters in the given word ELEPHANT, out of which L is repeated.
Hence, we can write the following set in the roaster form as given below:
T = {E, L, P, H, A, N, T}
(f). U = The set of all letters in the word DIVISION
There are 8 letters in the given word DIVISION, out of which I is repeated.
Hence, we can write the following set in the roaster form as given below:
U = {D, I, V, S, O, N}
Q.4: Write the given sets in set-builder form:
(a). {4, 8, 12, 16, 20}
(b). {3, 9, 27, 81}
(c). {4, 16, 64, 256, 1024}
(d). {1, 3, 5, 7…}
(e). {1, 8, 27, 64….1000}
Answer: Based on the formulae given in Sets
(a). {4, 8, 12, 16, 20} = {y: y = 4n, \(n\in\:P\:and\:1\leq n\leq 5\)}
(b). {3, 9, 27, 81}
We can see here that \(3=3^{1}\), \(9=3^{2}\), \(27=3^{3}\), \(81=3^{4}\).
Hence, {3, 9, 27, 81} = {y: y = 3n, \(n\in\:P\:and\:1\leq n\leq 4\)
(c). {4, 16, 64, 256, 1024}
We can see here that \(4=4^{1},16=4^{2},64=4^{3},256=4^{4},1024=4^{5}\)
Hence, {4, 16, 64, 256, 1024} = {y: y = 4n, \(n\in\:P\:and\:1\leq n\leq 5\)
(d). {1, 3, 5, 7…}
Above mentioned that the numbers are the set of odd natural numbers.
Hence, {1, 3, 5, 7…} = {y: y is an odd natural numbers}
(e). {1, 8, 27, 64….1000}
We can see here that \(1=1^{3},2=2^{3},3=3^{3},4=4^{3},…1000=10^{3}\)
Hence, {1, 8, 27, 64….1000} = {y: y = n2, \(n\in\:P\:and\:1\leq n\leq 10\)
Q.5: List all the elements from the given sets:
(a). P = {y: y is even natural number}
(b). Q = {y: y is an integer, \(\frac{-1}{2}< y< \frac{9}{2}\)}
(c). R = {y: y is an integer; \(y^{2}\leq 4\)}
(d). S = {y: y is letter in the word “TIFFIN”}
(e). T = {y: y is a month of a year having 31 days}
(f). U = {y: y is a consonant in the English alphabet which precedes m}
Answer: Based on the formulae given in Sets
(a). P = {y: y is even natural number} = {2, 4, 6, 8, 10 …..}
(b). Q = {y: y is an integer, \(\frac{-1}{2}< y< \frac{9}{2}\)}
We can see that \(\frac{-1}{2}=0.5\:and\:\frac{9}{2}=4.5\)
Hence, Q = {0, 1, 2, 3, 4}
(c). R = {y: y is an integer; \(y^{2}\leq 4\)}
We can see that \(\left ( -1 \right )^{2}=1\leq 4;\left ( -2 \right )^{2}=4\leq 4;\left ( -3 \right )^{2}=9> 4\)
\(\Rightarrow\) \(0^{2}=0\leq 4\)
\(\Rightarrow\) \(1^{2}=1\leq 4\)
\(\Rightarrow\) \(2^{2}=4\leq 4\)
\(\Rightarrow\) \(3^{2}=9> 4\)
Hence, R = {-2, -1, 0, 1, 2}
(d). S = {y: y is letter in the word “TIFFIN”}
= {T, I, F, N}
(e). T = {y: y is a month of a year having 31 days}
= {January, March, May, July, September, November}
(f). U = {y: y is a non-vowel alphabet in English which comes before m}
= {b, c, d, f, g, h, j, k, l}
Q.6: Match the following:
| (A) | {1, 2, 3, 6} | (i) | {y: y is a divisor of 6 and also a prime number} |
| (B) | {T, R, I, G, O, N, M, E, Y} | (ii) | {y: y is less than 10 and also an odd number} |
| (C) | {2, 3} | (iii) | {y: y is natural number divisor of 6} |
| (D) | {1, 3, 5, 7, 9} | (iv) | {y: y is a letter of the word TRIGONOMETRY} |
Answer:
| (A) | {1, 2, 3, 6} | (iii) | {y: y is natural number divisor of 6} |
| (B) | {T, R, I, G, O, N, M, E, Y} | (iv) | {y: y is a letter of the word TRIGONOMETRY} |
| (C) | {2, 3} | (i) | {y: y is a divisor of 6 and also a prime number} |
| (D) | {1, 3, 5, 7, 9} | (ii) | {y: y is less than 10 and also an odd number} |
Exercise 1.2
Q.1: Which of the following given below is null set?
(i). Set of odd natural numbers which is divisible by 2.
(ii). Set of even numbers which are prime
(iii). {x: x is a natural number, \(x < 5\) and \(x > 7\)}
(iv). {y: y is a point common to any two parallel lines}
Answer: Based on the formulae given in Sets
(i). A set of odd natural numbers which are divisible by 2 is a null set as none of the odd numbers is divisible by 2.
(ii). A set of even prime numbers is not null set as there is number 2 which is prime and also divisible by 2.
(iii). {x: x is a natural number, \(x < 5\) and \(x > 7\)} is a null set as any number cannot be less than 5 and also greater than 7.
(iv). {y: y is a point common to any two parallel lines} is a null set as parallel lines do not intersect. Therefore, there is no common point.
Q.2: State whether the following sets are infinite or finite:
(i). A set of months of a year.
(ii). {1, 2, 3 ….}
(iii). {1, 2, 3…99, 100}
(iv). The set of positive integers which are greater than 100.
(v). The set of prime numbers which are less than 99
Answer: Based on the formulae given in Sets
(i). The set of months of a year has 12 elements. Therefore, it is a finite set.
(ii). {1, 2, 3 ….} has infinite numbers in the set. Therefore, it is infinite set.
(iii). {1, 2, 3…99, 100} has elements from 1 to 100. Therefore, it is finite set.
(iv). The set of positive integers which are greater than 100 has infinite elements as there are infinite such elements. Therefore, it I infinite set.
(v). The set of prime numbers which are less than 99 has finite numbers in this set which is less than 99. Therefore, it is finite set.
Q.3: State whether the following sets are infinite or finite:
(i). The set of lines parallel to the x – axis.
(ii). The set of letters in the vowels.
(iii). The set of numbers multiple of 10.
(iv). The set of humans living on Earth.
(v). The set of circles passing through the origin (0, 0).
Answer: Based on the formulae given in Sets
(i). The set of lines which are parallel to the x-axis has infinite elements. Therefore, it is an infinite set.
(ii). The set of letters in the vowels has a finite element that is 5 elements. Therefore, it is a finite set.
(iii). The set of numbers which are multiple of 5 has infinite elements. Therefore, it is an infinite set.
(iv). The set of animals living on the earth has a finite number of elements. Therefore, it is finite set.
(v). The set of circles passing through the origin (0, 0) has infinite elements as number of circles can pass through the origin. Therefore, it is an infinite set.
Q.4: In the following set given below, state whether A = B or not:
(i). A = {w, x, y, z}
B = {z, y, x, w}
(ii). A = {5, 9, 13, 17}
B = {9, 5, 17, 19}
(iii). A = {4, 2, 6, 10, 8}
B = {x: x is positive even integer and \(x \leq 10\) }
(iv). A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}
Answer: Based on the formulae given in Sets
(i). A = {w, x, y, z}
B = {z, y, x, w}
Both the sets have same elements but the order is different. Therefore, A = B
(ii). A = {5, 9, 13, 17}
B = {9, 5, 17, 19}
It can be seen that 13 \(\in\) A but 13 \(\notin\) B. Therefore A ≠ B
(iii). A = {4, 2, 6, 10, 8}
B = {x: x is positive even integer and \(x \leq 10\) }
= {2, 4, 6, 8, 10}
Therefore, A = B
(iv). A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}
It can be seen that 15 \(\in\) B but 15 \(\notin\) A.
Therefore A ≠ B
Q.5 In the following set given below, is the pair of sets equal?
(i). A = {3, 4}
B = {y: y is solution of \(y^{2} + 5y + 6 = 0\)}
(ii). A = {a: a is a letter in the word FOLLOW}
B = {b: b is a letter in the word WOLF}
Answer: Based on the formulae given in Sets
(i) A = {3, 4}
B = {y: y is solution of \(y^{2} + 5y + 6 = 0\)}
The equation given \(y^{2} + 5y + 6 = 0\) can be solved as:
y (y + 3) + 2(y + 3) = 0
(y + 2) (y + 3) = 0
y = –2 or y = –3
Therefore, A = {2, 3} and B = {–2, –3}
Therefore, A ≠ B
(ii) A = {x: x is a letter in the word FOLLOW}
= {F, O, L, W}
B = {y: y is a letter in the word WOLF}
= {W, O, L, F}
Both the sets have same elements but the order is different.
Therefore, A = B
Q.6: From the following sets, select equal sets:
A = {2, 4, 8, 12}
B = {1, 2, 3, 4}
C = {4, 8, 12, 14}
D = {3, 1, 4, 2}
E = {–1, 1}
F = {0, a}
G = {1, –1}
H = {0, 1}
Answer: Based on the formulae given in Sets
A = {2, 4, 8, 12}
B = {1, 2, 3, 4}
C = {4, 8, 12, 14}
D = {3, 1, 4, 2}
E = {–1, 1}
F = {0, a}
G = {1, –1}
H = {0, 1}
We can see that:
8 \(\in\) A, 8 \(\notin\) B, 8 \(\notin\) D, 8 \(\notin\) E, 8 \(\notin\) F, 8 \(\notin\) G and 8 \(\notin\) H
Therefore, A ≠ B, A ≠ D, A ≠ E, A ≠ F, A ≠ G and A ≠ H
Also,
2 \(\in\) A and 2 \(\notin\) C
Therefore, A ≠ B
Also, 3 \(\in\) B, 3 \(\notin\) C, 3 \(\notin\) E, 3 \(\notin\) F, 3 \(\notin\) G and 3 \(\notin\) H
Therefore, B ≠ C, B ≠ E, B ≠ F, B ≠ G, B ≠ H
Also,
12 \(\in\) C, 12 \(\notin\) D, 12 \(\notin\) E, 12 \(\notin\) F, 12 \(\notin\) G, 12 \(\notin\) H
Therefore, C ≠ D, C ≠ E, C ≠ F, C ≠ G and C ≠ H
Also,
4 \(\in\) D, 4 \(\notin\) E, 4 \(\notin\) F, 4 \(\notin\) G, 4 \(\notin\) H
Therefore, D ≠ E, D ≠ F, D ≠ G, D ≠ H
Similarly, E ≠ F, E ≠ G, E ≠ H, F ≠ G, F ≠ H and G ≠ H
The order in which elements of the set are listed is not significant.
Therefore, B = D and E = G
Therefore, they are equal.
Exercise 1.3
Q.1: Fill in the blanks properly using \(\subset\) and \(\not\subset\).
(i). {3, 4, 5} ____ {2, 3, 4, 5, 6}
(ii). {a, b, c} ____ {d, c, d}
(iii). {y: y is a pupil of Class 11 of the school} ____ {y: y is students of the school}
(iv). {y: y is a circle in the plane} ____ {y: y is a circle in the same plane with radius 2 unit}
(v). {y: y is an equilateral triangle in a plane} ____ {y: y is a rectangle in the same plane}
(vi). {y: y is an equilateral triangle in a plane} ____ {y: y is a triangle in the plane}
(vii). {y: y is an odd natural number} ____ {x: x is an integers}
Answer: Based on the formulae given in Sets
(i). {3, 4, 5} \( \boldsymbol{\subset}\) {2, 3, 4, 5, 6}
(ii). {a, b, c} \( \boldsymbol{\not\subset}\) {d, c, d}
(iii). {y: y is a pupil of Class 11 of the school} \( \boldsymbol{\subset}\) {y: y is students of the school}
(iv). {y: y is a circle in the plane} \( \boldsymbol{\not\subset}\) {y: y is a circle in the same plane with radius 2 unit}
(v). {y: y is an equilateral triangle in a plane} \( \boldsymbol{\not\subset}\) {y: y is a rectangle in the same plane}
(vi). {y: y is an equilateral triangle in a plane} \( \boldsymbol{\not\subset}\) {y: y is a triangle in the plane}
(vii). {y: y is an odd natural number} \( \boldsymbol{\subset}\) {x: x is an integers}
Q.2: State whether the given statements are true or false:
(i). {b, c} \(\not\subset\) {c, d, e}
(ii). {a, e, i} \(\subset\) {x: x is a vowel in the English alphabets}
(iii). {1, 2, 3} \(\subset\){1, 2, 4, 5}
(iv). {c} \(\subset\) {b, c, d}
(v). {b} \(\in\) {a, b, c, d}
(vi). {y: y is an even natural no. less than 6} \(\subset\) {y: y is a natural no. which can divide 36}
Answer: Based on the formulae given in Sets
(i). False
Since, Each element of {d, c} is present in {c, d, e}
(ii). True
Since, a, e and i are the three vowels of the English alphabet.
(iii). False
Since, 3 \(\in\) {1, 2, 3} but 3 \(\notin\) {1, 2, 4, 5}
(iv). True
Since, Element c of {c} is also present in {b, c, d}.
(v). False
Since, Element b of {b} is also present in {a, b, c, d}.
(vi). True
Since, {y: y is an even natural number less than 6} = {2, 4}
{y: y is a natural no. which can divide 36} = {1, 2, 3, 4, 6, 9, 12, 18, 36}
Each elements of {2, 4} are present in {1, 2, 3, 4, 6, 9, 12, 18, 36}
Q.3: Let X = {11, 12, {13, 14}, 15}. According to the given set which of the given statements are false? Explain why.
(i). {13, 14} \(\subset\) X
(ii). {13, 14} \(\in\) X
(iii). {{13, 14}} \(\subset\) X
(iv). 11 \(\in\) X
(v). 11 \(\subset\) X
(vi). {11, 12, 15} \(\subset\) X
(vii). {11, 12, 15} \(\in\) X
(viii). {11, 12, 13} \(\subset\) X
(ix). Ø \(\in\) X
(x). Ø \(\subset\) X
(xi). {Ø} \(\subset\) X
Answer: Based on the formulae given in Sets
Given:
X = {11, 12, {13, 14}, 15}
(i). The Statement {13, 14} \(\subset\) X is False
Since, 13 \(\in\) {13, 14}
But, 13 \(\notin\) X
(ii). The Statement {13, 14} \(\in\) X is True
Since, {13, 14} is an element of X
(iii). The Statement {{13, 14}} \(\subset\) X is True
Since, {13, 14} \(\in\) {{13, 14}} and {13, 14} \(\in\) X
(iv). The Statement 11 \(\in\) X is True
Since, 11 is an element of X
(v). The Statement 11 \(\subset\) X is False
Since, an element of a set can never be subset of itself.
(vi). The Statement {11, 12, 15} \(\subset\) X is True
Since, each element of {11, 12, 15} is present in X
(vii). The Statement {11, 12, 15} \(\in\) X is False
Since, {11, 12, 13} is not an element of X.
(viii). The Statement {11, 12, 13} \(\subset\) X is False
Since, 13 \(\in\) {11, 12, 13}
But, 13 \(\notin\) X
(ix). The Statement Ø\(\in\) X is False
Since, X does not contain element Ø
(x). The Statement Ø\(\subset\) X is True
Since, Ø is subset of every set.
(xi). The Statement {Ø} \(\subset\) X is False
Since, Ø\(\in\) {Ø}
Ø\(\in\) X.
Q.4: Write all the subsets of the given sets:
(i). {b}
(ii). {b, c}
(iii). {2, 3, 4}
(iv). Ø
Answer: Based on the formulae given in Sets
(i). {b}:
Subsets are as given: Ø and {b}
(ii). {b, c}:
Subsets are as given: Ø, {b}, {c} and {b, c}
(iii). {2, 3, 4}:
Subsets are as given: Ø, {2}, {3}, {4}, {2, 3}, {3, 4}, {4, 2} and {2, 3, 4}
(iv). Ø:
Subsets are as given: Ø
Q.5: How many elements has P(X), if X = Ø ?
Answer: Based on the formulae given in Sets
If X has m elements that is n(X) = m, then n[P(X)] = \(2^{ m }\)
If X = Ø, then n(X) = 0
Therefore, n[P(X)] = \(2^{ 0 }\) = 1
Therefore, P(X) has one element.
Q.6: Write the given in the form of intervals:
(i). {y: y \(\in\) R, –5 < y ≤ 7}
(ii). {y: y \(\in\) R, –13 < y < –11}
(iii). {y: y \(\in\) R, 1 ≤ y < 8}
(iv). {y: y \(\in\) R, 4 ≤ y ≤ 5}
Answer: Based on the formulae given in Sets
(i). {y: y \(\in\) R, –5 < y ≤ 7} = (-5, 7]
(ii). {y: y \(\in\) R, –13 < y < –11} = (-13, -11)
(iii). {y: y \(\in\) R, 1 ≤ y < 8} = [1, 8)
(iv). {y: y \(\in\) R, 4 ≤ y ≤ 5} = [4, 5]
Q.7: Write the given intervals in the form of set – builder:
(i). (–4, 1)
(ii). [7, 13]
(iii). (7, 13]
(iv). [–24, 6)
Answer: Based on the formulae given in Sets
(i). (–4, 1) = {y: y \(\in\) R, -4 < y < 1}
(ii). [7, 13] = {y: y \(\in\) R, 7 \(\leq\) y \(\leq\) 13}
(iii). (7, 13] = {y: y \(\in\) R, 7 < y \(\leq\) 13}
(iv). [–24, 6) = {y: y \(\in\) R, –24 \(\leq\) x < 6}
Q.8: What universal set/ sets would you propose for the given sets?
(i). The set of right triangles
(ii). The set of isosceles triangles
Answer: Based on the formulae given in Sets
(i). The set of right triangles
Proposed universal sets are:
- The set of triangles
- The set of polygons
(ii). The set of isosceles triangles
Proposed universal sets are:
- The set of triangles
- The set of polygons
- The set of two – dimensional figures
Q.9: X = {1, 3, 5}, Y = {2, 4, 6} and Z = {0, 2, 4, 6, 8}
Which of the given sets can be considered as the universal set for the given sets X, Y and Z?
(i). {0, 1, 2, 3, 4, 5, 6}
(ii). Ø
(iii). {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv). {1, 2, 3, 4, 5, 6, 7, 8}
Answer: Based on the formulae given in Sets
(i). {0, 1, 2, 3, 4, 5, 6}
X \(\subset\) {0, 1, 2, 3, 4, 5, 6}
Y \(\subset\) {0, 1, 2, 3, 4, 5, 6}
Z \(\not\subset\) {0, 1, 2, 3, 4, 5, 6}
Therefore, the set {0, 1, 2, 3, 4, 5, 6} cannot be the universal set for the sets X, Y and Z.
(ii). Ø
X \(\not\subset\) Ø
Y \(\not\subset\) Ø
Z \(\not\subset\) Ø
Therefore, the set Ø cannot be the universal set for the sets X, Y and Z.
(iii). {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
X \(\subset\) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Y \(\subset\) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Z \(\subset\) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Therefore, the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is the universal set for the sets X, Y and Z.
(iv). {1, 2, 3, 4, 5, 6, 7, 8}
X \(\subset\) {1, 2, 3, 4, 5, 6, 7, 8}
Y \(\subset\) {1, 2, 3, 4, 5, 6, 7, 8}
Z \(\not\subset\) {1, 2, 3, 4, 5, 6, 7, 8}
Therefore, the set {1, 2, 3, 4, 5, 6, 7, 8} cannot be the universal set for the sets X, Y and Z.
Exercise 1.4
Q.1: Find the union of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ
Answer: Based on the formulae given in Sets
(i).
Given:
P = {1, 4, 6} and Q = {1, 3, 4}
Therefore, P \(\cup\) Q = {1, 3, 4, 6}
(ii).
Given:
X = {a, e, i, o, u} and Y = {x, y, z}
Therefore, X \(\cup\) Y = {x, y, z, a, e, i, o, u}
(iii).
Given:
X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 5}
X = {3, 6, 9 ….}
Y = {1, 2, 3, 4}
X \(\cup\) Y = {1, 2, 3, 4, 6, 9 …. }
Therefore, X \(\cup\) Y = {a:a = 1, 2, 3, 4 or multiple of 3}
(iv).
Given:
X = {x: x is a natural number and 1 < x ≤ 5} = {2, 3, 4, 5}
Y = {x: x is a natural number and 5 < x < 10} = {6, 7, 8, 9}
X \(\cup\) Y = {2, 3, 4, 5, 6, 7, 8, 9}
Therefore, X \(\cup\) Y = {a:a \(\in\) N and \(1 < a < 10\)}
(v).
Given:
X = {4, 5, 6} and Y = Φ
Therefore, X \(\cup\) Y = {4, 5, 6}
Q.2: Let A = {x, y} and B = {x, y, z}
Is A ⊂ B? What is A ∪ B?
Answer: Based on the formulae given in Sets
Given:
A = {x, y} and B = {a, b, c}
Yes, A \(\subset\) B that is A is subset of B.
Therefore, A \(\cup\) B = {a, b, c} = B
Q.3: If X and Y are two sets such that X \(\subset\) Y, then what is X \(\cup\) Y?
Answer:
If X and Y are two sets such that X \(\subset\) Y, then X \(\cup\) Y = Y as all the elements of set X are present in set Y.
Q.4: If P = {1, 2, 3, 4}, Q = {3, 4, 5, 6}, R = {5, 6, 7, 8} and S = {7, 8, 9, 10}
Find the following:
(i). P \(\cup\) Q
(ii). P \(\cup\) R
(iii). Q \(\cup\) R
(iv). Q \(\cup\) S
(v). P \(\cup\) Q \(\cup\) R
(vi). P \(\cup\) Q \(\cup\) S
(vii). Q \(\cup\) R \(\cup\) S
Answer: Based on the formulae given in Sets
Given:
P = {1, 2, 3, 4]
Q = {3, 4, 5, 6}
R= {5, 6, 7, 8} and,
S = {7, 8, 9, 10}
Now,
(i). P \(\cup\) Q = {1, 2, 3, 4, 5, 6}
(ii). P \(\cup\) R = {1, 2, 3, 4, 5, 6, 7, 8}
(iii). Q \(\cup\) R = {3, 4, 5, 6, 7, 8}
(iv). Q \(\cup\) S = {3, 4, 5, 6, 7, 8, 9, 10}
(v). P \(\cup\) Q \(\cup\) R = {1, 2, 3, 4, 5, 6, 7, 8}
(vi). P \(\cup\) Q \(\cup\) S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii). Q \(\cup\) R \(\cup\) S = {3, 4, 5, 6, 7, 8, 9, 10}
Q.5: Find the intersection of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ
Answer: Based on the formulae given in Sets
(i).
Given:
P = {1, 4, 6} and Q = {1, 3, 4}
Therefore, P \(\cap\) Q = {1, 3}
(ii).
Given:
X = {a, e, i, o, u} and Y = {x, y, z}
Therefore, X \(\cap\) Y = Φ
(iii).
Given:
X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 5}
X = {3, 6, 9 ….}
Y = {1, 2, 3, 4}
Therefore, X \(\cap\) Y = {3}
(iv).
Given:
X = {x: x is a natural number and 1 < x ≤ 5} = {2, 3, 4, 5}
Y = {x: x is a natural number and 5 < x < 10} = {6, 7, 8, 9}
Therefore, X \(\cap\) Y = Φ
(v). X = {4, 5, 6} and Y = Φ
Therefore, X \(\cap\) Y = Φ
Q.6: If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}
Find the following:
(i). A \(\cap\) B
(ii). B \(\cap\) C
(iii). A \(\cap\) C \(\cap\) D
(iv). A \(\cap\) C
(v). B \(\cap\) D
(vi). A \(\cap\) (B \(\cup\) C)
(vii). A \(\cap\) D
(viii). A \(\cap\) (B \(\cup\) D)
(ix). (A \(\cap\) B) \(\cap\) (B \(\cup\) C)
(x). (A\(\cup\) D) \(\cap\) (B \(\cup\) C)
Answer: Based on the formulae given in Sets
(i). A \(\cap\) B = {7, 9, 11}
(ii). B \(\cap\) C = {11, 13}
(iii). A \(\cap\) C \(\cap\) D
= {A \(\cap\) C} \(\cap\) D
= {11} \(\cap\) {15, 17} = Φ
(iv). A \(\cap\) C = {11}
(v). B \(\cap\) D = Φ
(vi). A \(\cap\) (B \(\cup\) C)
= (A \(\cap\) B) \(\cup\) (A \(\cap\) C)
= {7, 9, 11} \(\cup\) {11}
= {7, 9, 11}
(vii). A\(\cap\) D = Φ
(viii). A\(\cap\) (B \(\cup\) D)
= (A \(\cap\) B) \(\cup\) (A \(\cap\) D)
= (7, 9, 11} \(\cup\) Φ = {7, 9, 11}
(ix). (A \(\cap\) B) \(\cap\) (B \(\cup\) C)
= {7, 9, 11} ) \(\cap\) {7, 9, 11, 13, 15} = {7, 9, 11}
(x). (A\(\cup\) D) \(\cap\) (B \(\cup\) C)
= {3, 5, 7, 9, 11, 15, 17} ) \(\cap\) {7, 9, 11, 13, 15} = {7, 9, 11, 15}
Q.7: If A = {y: y is a natural number}, B ={y: y is an even natural number}, C = {y: y is an odd natural number} and D = {y: y is a prime number}
Find the following:
(i). A \(\cap\) B
(ii). A \(\cap\) C
(iii). A \(\cap\) D
(iv). B \(\cap\) C
(v). B \(\cap\) D
(vi). C \(\cap\) D
Answer: Based on the formulae given in Sets
A = {y: y is a natural number} = {1, 2, 3, 4, 5….}
B = {y: y is an even natural number} = {2, 4, 6, 8 ….}
C = {y: y is an odd natural number} = {1, 3, 5, 7, 9 ….}
D = {y: y is a prime number} = {2, 3, 5, 7….}
Now,
(i). A \(\cap\) B = {y: y is a natural number} = B
(ii). A \(\cap\) C = {y: y is an odd natural number} = C
(iii). A \(\cap\) D = {y: y is a prime number} = D
(iv). B \(\cap\) C = Φ
(v). B \(\cap\) D = {2}
(vi). C \(\cap\) D = {y: y is odd prime number}
Q.8: Which of the given pairs of sets are disjoint?
(i). A = {1, 2, 3, 4} and B = {x: x is a natural number and 4 ≤ x ≤ 6}
(ii). A = {a, e, i, o, u} and B = {c, d, e, f}
(iii). A = {x: x is an even integer} and B = {x: x is an odd integer}
Answer: Based on the formulae given in Sets
(i). A = {1, 2, 3, 4} and B = {x: x is a natural number and 4 ≤ x ≤ 6} = {4, 5, 6}
A \(\cap\) B = {1, 2, 3, 4} \(\cap\) {4, 5 6} = {4}
Therefore, this pair of set is not disjoint.
(ii). A = {a, e, i, o, u} and B = {c, d, e, f}
A \(\cap\) B = {a, e, i, o, u} \(\cap\) {c, d, e, f} = {e}
Therefore, this pair of set is not disjoint.
(iii). A = {x: x is an even integer} and B = {x: x is an odd integer}
A \(\cap\) B = {x: x is an even integer} \(\cap\) {x: x is an odd integer} = Φ
Therefore, this pair of set is disjoint.
Q.9: If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}
Find the following:
(i). A – B
(ii). A – C
(iii). A – D
(iv). B – A
(v). C – A
(vi). D – A
(vii). B – C
(viii). B – D
(ix). C – B
(x). D – B
(xi). C – D
(xii). D – C
Answer: Based on the formulae given in Sets
(i). A – B = {3, 6, 9, 15, 18, 21}
(ii). A – C = {3, 9, 15, 18, 21}
(iii). A – D = {3, 6, 9, 12, 18, 21}
(iv). B – A = {4, 8, 16, 20}
(v). C – A = {2, 4, 8, 10, 14, 16}
(vi). D – A = {5, 10, 20}
(vii). B – C = {20}
(viii). B – D = {4, 8, 12, 16}
(ix). C – B = {2, 6, 10, 14}
(x). D – B = {5, 10, 15}
(xi). C – D = {2, 4, 6, 8, 12, 14, 16}
(xii). D – C = {5, 15, 20}
Q.10: If X = {a, b, c, d} and Y = {f, b, d, g}
Find the following:
(i). X – Y
(ii). Y – X
(iii). X \(\cap\) Y
Answer: Based on the formulae given in Sets
(i). X – Y = {a, c}
(ii). Y – X = {f, g}
(iii). X \(\cap\) Y = {b, d}
Q.11: What is R – Q, if R is the set of real numbers and Q is the set of rational?
Answer:
R: Set of real numbers
Q: Set of rational numbers
Hence, R – Q is a set of irrational numbers.
Q.12: State whether the following statements are true or false. Give reason.
(i). A = {2, 3, 4, 5} and B = {3, 6} are disjoint sets.
(ii). A = {a, e, i, o, u } and B = {a, b, c, d} are disjoint sets.
(iii). A = {2, 6, 10, 14} and B = {3, 7, 11, 15} are disjoint sets.
(iv). A = {2, 6, 10} and B = {3, 7, 11} are disjoint sets.
Answer: Based on the formulae given in Sets
(i). False
Because, 3 \(\in\) {2, 3, 4, 5} and 3 \(\in\) {3, 6}
A \(\cap\) B = {2, 3, 4, 5} \(\cap\) {3, 6} = {3}
(ii). False
Because, a \(\in\) {a, e, i, o, u} and a \(\in\) {a, b, c, d}
A \(\cap\) B = {a, e, i, o, u } \(\cap\) {a, b, c, d} = {a}
(iii). True
Because, A \(\cap\) B= {2, 6, 10, 14} \(\cap\) {3, 7, 11, 15} = Φ
(iv). True
Because, A \(\cap\) B = {2, 6, 10} \(\cap\) {3, 7, 11} = Φ
Exercise 1.5
Q.1: Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
X = {1, 2, 3, 4, 5}
Y = {2, 4, 6} and
Z = {2, 4, 5, 6}.
Find the following sets:
(i). X’
(ii). Y’
(iii). \((X \cup Y)’\)
(iv). \((X \cup Z)’\)
(v). \((X’)^{‘}\)
(vi). \((Y – Z)’\)
Answer: Based on the formulae given in Sets
Given:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
X = {1, 2, 3, 4, 5}
Y = {2, 4, 6, 9} and
Z = {2, 4, 5, 6}
(i). X’ = {6, 7, 8, 9}
(ii). Y’ = {1, 3, 5, 7, 8, 9}
(iii). \((X \cup Y)’\)
And, \((X \cup Y)\)= {1, 2, 3, 4, 5, 6, 9}
Therefore, \((X \cup Y)’\)= {7, 8}
(iv). \((X \cup Z)’\)
And, \((X \cup Z)\) = {1, 2, 3, 4, 5, 6}
Therefore, \((X \cup Z)’\) = {7, 8, 9}
(v). \((X’)^{ ‘ }\) = X = {1, 2, 3, 4, 5}
(vi). \((Y – Z)’\)
Since, (Y – Z) = {9}
Therefore, (Y – Z)’ = {1, 2, 3, 4, 5, 6, 7, 8}
Q.2: If U = {a, b, c, d, e, f, g, h}, find the complements of the given sets:
(i). W = {a, b, c}
(ii). X = {d, e, f, g}
(iii). Y = {a, c, e, g}
(iv). Z = {f, g, h, a}
Answer: Based on the formulae given in Sets
Given:
U = {a, b, c, d, e, f, g, h}
(i). W = {a, b, c}
W’ = {d, e, f, g, h}
(ii). X = {d, e, f, g}
X’ = {a, b, c}
(iii). Y = {a, c, e, g}
Y’ = {b, d, f}
(iv). Z = {f, g, h, a}
Z’ = {b, c, d, e}
Q.3: Take natural numbers as the universal set. Write the complements of the given sets:
(i). A = {y: y is an even natural number}
(ii). B = {y: y is an odd natural number}
(iii). C = {y: y is a positive multiple of 3}
(iv). D = {y: y is a prime number}
(v). E = {y: y is a natural number divisible by 3 and 5}
(vi). F = {y: y is a perfect square}
(vii). G = {y: y is perfect cube}
(viii). H = {y: y + 5 = 8}
(ix). I = {y: 2y + 5 = 9}
(x). J = {y: y \(\geq\) 7}
(xi). K = {y: y \(\in\) N and 2y + 1 > 10}
Answer: Based on the formulae given in Sets
Given:
U = set of natural numbers = N
(i). A’ = {y: y is an even natural number}’
= {y: y is an odd natural number}
(ii). B’ = {y: y is an odd natural number}
= {y: y is an even natural number}
(iii). C’ = {y: y is a positive multiple of 3}’
= {y: y \(\in\) N and y is not a multiple of 3}
(iv). D’ = {y: y is a prime number}’
= {y: y is a positive composite number and y = 1}
(v). E’ = {y: y is a natural number divisible by 3 and 5}’
= {y: y is a natural number that is not divisible by 3 or 5}
(vi). F’ = {y: y is a perfect square}’
= {y: y \(\in\) N and y is not a perfect square}
(vii). G’ = {y: y is perfect cube}’
= {y: y \(\in\) N and y is not a perfect cube}
(viii). H’ = {y: y + 5 = 8}’
= {y: y \(\in\) N and y \(\neq\) 3}
(ix). I’ = {y: 2y + 5 = 9}’
= {y: y \(\in\) N and y \(\neq\) 2}
(x). J’ = {y: y \(\geq\) 7}’
= {y: y \(\in\) N and x < 7}
(xi). K’ = {y: y \(\in\) N and 2y + 1 > 10}
= {y: y \(\in\) N and y \(\leq \frac{ 9 }{ 2 }\)}
Q.4: If U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8} and, B = {2, 3, 5, 7}.
Verify that:
(i). \((A\cup B)’\) = \(A’\cap B’\)
(ii). \((A\cap B)’\) = \(A’\cup B’\)
Answer: Based on the formulae given in Sets
Given:
U = {1, 2, 3, 4, 5,6,7,8, 9}
A = {2, 4, 6, 8} and B = {2, 3, 5, 7}
(i). \((A\cup B)’\)
= {2, 3, 4, 5, 6, 7, 8}’ = {1, 9}
Now, \(A’\cap B’\) = {1, 3, 5, 7, 9} \(\cap\) {1, 4, 6, 8, 9} = {1, 9}
Therefore, \((A\cup B)’\) = \(A’\cap B’\)
(ii). \((A\cap B)’\)
= {2}’ = {1, 3, 4, 5, 6, 7, 8, 9}
Now, \(A’\cup B’\) = {1, 3, 5, 7, 9} \(\cup\) {1, 4, 6, 8, 9} = {1, 3, 4, 5, 6, 7, 8, 9}
Therefore, \((A\cap B)’\) = \(A’\cup B’\)
Q.5: Draw the Venn diagrams for the following:
(i). \((A \cup B)’\)
(ii). \(A’ \cap B’\)
(iii). \((A \cap B)’\)
(iv). \(A’ \cup B’\)
Answer: Based on the formulae given in Sets
(i). \((A \cup B)’\):
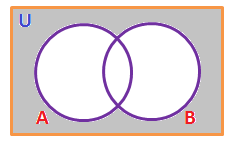
(ii). \(A’ \cap B’\):
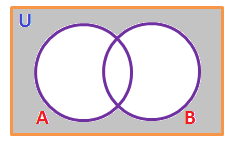
(iii). \((A \cap B)’\):
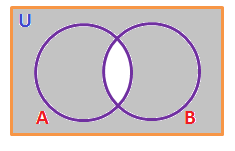
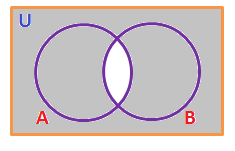
(iv). \(A’ \cup B’\):
Q.6: Let U be the universal set that is the set of all triangles in a plane. If X is the set of all triangles with at least one angle different from \(60^{\circ}\), what is X’ ?
Answer: Based on the formulae given in Sets
X’ is the set of all equilateral triangles.
Q.7: Complete the given statements using proper symbols:
(i). \(A \cup A’\)
(ii). Ø \(\cap A\)
(iii). \(A \cap A’\)
(iv). \(U’ \cap A\)
Answer: Based on the formulae given in Sets
(i). \(A \cup A’\) = U
(ii). Ø \(\cap A\) = \(U \cap A\) = A
(iii). \(A \cap A’\) = Ø
(iv). \(U’ \cap A\) = Ø \(\cap A\) = Ø
Practice Exercise 1.6
Q.1: If A and B are two sets such that n(A) = 16, n(B) = 24 and \(n\;(A \cup B)\) = 39. Find \(n\;(A \cap B)\).
Answer: Based on the formulae given in Sets
Given:
n(A) = 16, n(B) = 23 and \(n\;(A \cup B)\) = 39
As we know that \(n\;(A \cup B) \; = \; n(A) \; + \; n(B) \; – \; n(A \cap B)\)
39 = 16 + 24 – \(n\;(A \cap B)\)
\(n\;(A \cap B)\) = 40 – 39 = 1
Therefore, \(n\;(A \cap B)\) = 1
Q.2: If A and B are two sets such that \(A \cup B\) has 17 elements, A has 9 elements and B has 14 elements. How many elements does \(A \cap B\) have?
Answer: Based on the formulae given in Sets
Given:
n(A) = 9, n(B) = 14 and, \(n(A \cup B)\) = 17
As we know that \(n\;(A \cup B) \; = \; n(A) \; + \; n(B) \; – \; n\;(A \cap B)\)
17 = 9 + 14 – \(n\;(A \cap B)\)
\(n\;(A \cap B)\) = 23 – 17 = 6
Therefore, \(A \cap B\) = 6
Q.3: In a group there are 450 people, 200 speaks Hindi and 270 can speak English. How many people can speak both English and Hindi?
Answer: Based on the formulae given in Sets
Let us assume that:
H = the set of people who speaks Hindi
And, E = the set of people who speaks English
Given:
\(n\;(H \cup E)\) = 450, n(H) = 200 and n(E) = 270
\(n\;(H \cap E)\) = ?
As we know that, \(n\;(H \cup E) \; = \; n(H) \; + \; n(E) \; – \; n\;(H \cap E)\)
450 = 200 + 270 – \(n\;(H \cap E)\)
450 = 470 – \(n\;(H \cap E)\)
\(n\;(H \cap E)\) = 470 – 450
\(n\;(H \cap E)\) = 20
Therefore, 20 people can speak both English and Hindi.
Q.4: If X and Y are two sets such that X has 22 elements, Y has 34 elements, and \(n\;(X \cap Y)\) has 10 elements, how many elements does \(n\;(X \cup Y)\) have?
Answer: Based on the formulae given in Sets
Given:
\(n\;(X \cap Y)\) = 10, n(X) = 22 and, n(Y) = 34
\(n\;(X \cup Y)\) = ?
As we know that, \(n\;(X \cup Y) \; = \; n(X) \; + \; n(Y) \; – \; n\;(X \cap Y)\)
\(n\;(X \cup Y)\) = 22 + 34 – 10
\(n\;(X \cup Y)\) = 56 – 10
\(n\;(X \cup Y)\) = 46
Therefore, the set \(n\;(X \cup Y)\) has 46 elements.
Q.5: If A and B are two sets such that A has 45 elements, n (A ∩ B) has 15 elements and n (A ∪ B) has 70 elements, how many elements does B have?
Answer: Based on the formulae given in Sets
Given:
n(A) = 45, \(n\;(A \cap B)\) = 15 and, \(n\;(A \cup B)\) = 70
n(B)= ?
As we know that, \(n\;(A \cup B) \; = \; n(A) \; + \; n(B) \; – \; n(A \cap B)\)
70 = 45 + n(B) – 15
70 = 30 + n(B)
n(B) = 40
Therefore, the set n(B) has 40 elements.
Q.6:There are 70 people, out of which 35 like tea, 55 like coffee, and each person likes at least one of the two beverages. How many people like both tea and coffee?
Answer: Based on the formulae given in Sets
Let us assume that:
T = the set of people who like tea
And, C = the set of people who like coffee
Given:
n(T) = 35, n(C) = 55 and \(n\;(C \cup T)\) = 70
\(n\;(C \cap T)\) = ?
As we know that \(n\;(C \cup T) \; = \; n(C) \; + \; n(T) \; – \; n\;(C \cap T)\)
70 = 55 + 35 – \(n\;(C \cap T)\)
70 = 90 – \(n\;(C \cap T)\)
\(n\;(C \cap T)\) = 20
Therefore, there are 20 people who like both tea and coffee.
Q.7: There are 70 students in a group, 35 like cricket, 15 like both tennis and cricket. How many like tennis only and not cricket? How many like tennis?
Answer: Based on the formulae given in Sets
Let us assume that:
C = the set of students who like cricket
And, T = the set of students who like tennis
Given:
n(C) = 35, \(n\;(C \cup T)\) = 70, \(n\;(C \cap T)\) = 15
n(T) = ?
As we know that \(n\;(C \cup T) \; = \; n\;(C) \; + \; n\;(T) \; – \; n\;(C \cap T)\)
70 = 35 + n(T) – 15
70 = 20 + n(T)
n(T) = 50
Therefore, there are 50 students who like to play tennis.
Now, \((T – C) \cup (T \cap C) \; = \; T\)
Also, \((T – C) \cap (T \cap C)\) = Ø
Therefore, n(T) = n(T – C) + \(n\;(T \cap C)\)
50 = n(T – C) + 15
n(T – C) = 50 – 15
n(T – C) = 35
Therefore, there are 35 students who play only tennis.
Q.8: In a committee, 60 people speak French, 30 speak Spanish and 20 speak both Spanish and French. How many speak at least one of these two languages?
Answer: Based on the formulae given in Sets
Let us assume that:
F = the set of people who speaks French
And, S = the set of people who speaks Spanish
Given:
n(F) = 60, n(S) = 30, \(n\;(F \cap S)\) = 20
\(n\;(F \cup S)\) = ?
As we know that \(n\;(S \cup F) \; = \; n(S) \; + \; n(F) \; – \; n\;(S \cap F)\)
\(n(F \cup S)\) = 30 + 60 – 20
\(n(F \cup S)\) = 70
Therefore, there are 70 people who can speak at least one of the two languages.