Facts
- Rational numbers can be represented in the form p/q where q ≠ 0. Irrational numbers cannot be represented in the form p/q where q ≠ 0. The decimal number expansion of a number is either terminating or non terminating recurring.
- The decimal expansion of an irrational number is non terminating, non recurring.
- The sum or difference of a rational number and an irrational number is irrational
- The product or quotient of a non-zero rational number with an irrational number is irrational.
- add, subtract, multiply or divide two irrationals, the result may be rational or irrational.
- √(ab) = √a*√b
- √a/√b = √(a/b)
- (√a+√b)(√a-√b) = a-b
- (a+√b)(a-√b) = a2-b
- (√a+√b)(√c+√d) = (√ac + √ad + √bc + √bd)
- (√a+√b)2= a + 2 √ab + b
Solved problems
Q. Show that 0.3333... = 03. can be expressed in the form p/q are such p,q are integers and q ≠ 0
Ans.let x = 0.333. Therefore 10 x = 3.333...
So we have 10x = 3 + 0.3333...
which is 10x=3+x and so x=1/3
Q.Show that 1.272727... can be expressed in the form p/q and p,q are integers and q ≠ 0.
- so let x=1.27272...
- we have 100x=127.2727...
- 100x=126+1.2727..
- 100x=126+x which gives x=126/99
Ans.x=14/11
Q.Show that 0.2353535.. can be expressed in the form p/q and p,q are integers and q ≠ 0.
so let x=0.2353535...
we have 100x=23.5353535...
100x=23.3+0.2353535..
100x=23.3+x which gives x=233/990
Ans.x=233/990
Long division method
Divide p(x) by g(x), where p(x) = x + 3x2 – 1 and g(x) = 1 + x.
Write the dividend x + 3x2 – 1 and the divisor 1 + x in the standard form, i.e., after arranging the terms in the descending order of their degrees. So, the + x –1 and divisor is x + 1. dividend is 3x2
We divide the first term of the dividend by the first term of the divisor, i.e., we divide 3x 2 by x, and get 3x. This gives us the first term of the quotient. i.e. 3x
We multiply the divisor by the first term of the quotient, and subtract this product from the dividend, i.e., we multiply x + 1 by 3x and subtract the product 3x2 + 3x from the dividend 3x2 + x – 1. This gives us the remainder as –2x – 1.
We treat the remainder –2x – 1 as the new dividend. The divisor remains the same. We repeat Step 2 to get the next term of the quotient, i.e., we divide the first term – 2x of the (new) dividend by the first term x of the divisor and obtain – 2. Thus, – 2 is the second term in the quotient.
We multiply the divisor by the second term of the quotient and subtract the product from the dividend. That is, we multiply x + 1 by – 2 and subtract the product – 2x – 2 from the dividend – 2x – 1. This gives us 1 as the remainder.
This process continues till the remainder is 0 or the degree of the new dividend is less than the degree of the divisor. At this stage, this new dividend becomes the remainder and the sum of the quotients gives us the whole quotient.
Thus, the quotient in full is 3x – 2 and the remainder is 1.
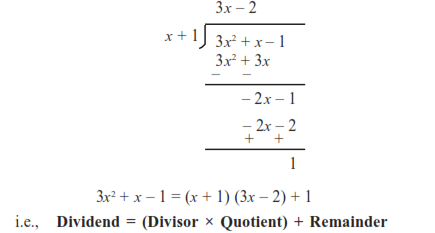
Polynomials and linear equations
Let p(x) be any polynomial of degree greater than or equal to one and let a be any real number. If p(x) is divided by the linear polynomial x – a, then the remainder is p(a).
If p(x) is a polynomial of degree n > 1 and a is any real number, then (i) x – a is a factor of p(x), if p(a) = 0, and (ii) p(a) = 0, if x – a is a factor of p(x).
(x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx
(x + y)3 = x3 + y3 + 3 xy (x + y)
(x - y)3 = x3 - y3 - 3 xy (x - y)
x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
Every linear equation in one variable has a unique solution. A linear equation in two variables has infinitely many solutions.
Fahrenheit = (9/5) * Celsius + 32
The graph of every linear equation in two variables is a straight line.
x = 0 is the equation of the y-axis and y = 0 is the equation of the x-axis. The graph of x = a is a straight line parallel to the y-axis. The graph of y = a is a straight line parallel to the x-axis.
An equation of the type y = mx represents a line passing through the origin.
Q.Find the remainder when x4 + x3 – 2x2 + x + 1 is divided by x – 1.
p(1) = (1)4 + (1)3 – 2(1)2 + 1 + 1 = 2
p(1) = 2
Ans.remainder = 2
Q.Examine whether x + 2 is a factor of x3 + 3x2 + 5x + 6 and of 2x+4.
x+2 gives a=-2. and so we can calculate P(-2)
P(-2) = 0
Ans.
Euclid's Postulates
A straight line may be drawn from any one point to any other point.
Given two distinct points, there is a unique line that passes through them
A terminated line can be produced indefinitely.
A circle can be drawn with any centre and any radius
All right angles are equal to one another.
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
For example, the line PQ in Fig. below falls on lines AB and CD such that the sum of the interior angles 1 and 2 is less than 180° on the left side of PQ. Therefore, the lines AB and CD will eventually intersect on the left side of PQ.

Geometry and Rules of Congruence
Two figures are congruent, if they are of the same shape and of the same size.
Two circles of the same radii are congruent.
Two squares of the same sides are congruent.
If two sides and the included angle of one triangle are equal to two sides and the included angle of the other triangle, then the two triangles are congruent (SAS Congruence Rule).
If two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, then the two triangles are congruent (ASA Congruence Rule).
If two angles and one side of one triangle are equal to two angles and the corresponding side of the other triangle, then the two triangles are congruent (AAS Congruence Rule).
Angles opposite to equal sides of a triangle are equal.
Sides opposite to equal angles of a triangle are equal.
Each angle of an equilateral triangle is of 60°.
If three sides of one triangle are equal to three sides of the other triangle, then the two triangles are congruent (SSS Congruence Rule).
If in two right triangles, hypotenuse and one side of a triangle are equal to the hypotenuse and one side of other triangle, then the two triangles are congruent (RHS Congruence Rule).
In a triangle, angle opposite to the longer side is larger (greater).
In a triangle, side opposite to the larger (greater) angle is longer.
Sum of any two sides of a triangle is greater than the third side.
A line through the mid-point of a side of a triangle parallel to another side bisects the third side.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral, in order, is a parallelogram
The line-segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of it
Diagonals of a square bisect each other at right angles and are equal, and vice-versa.
Diagonals of a rhombus bisect each other at right angles and vice-versa.
Diagonals of a rectangle bisect each other and are equal and vice-versa.
A diagonal of a parallelogram divides it into two congruent triangles.
A quadrilateral is a parallelogram, if (i) opposite sides are equal or (ii) opposite angles are equal or (iii) diagonals bisect each other or (iv)a pair of opposite sides is equal and parallel
Areas of Parallelograms and Triangles
Two congruent figures have equal areas but the converse need not be true.
Area of a parallelogram is the product of its base and the corresponding altitude.
If a parallelogram and a triangle are on the same base and between the same parallels, then area of the triangle is half the area of the parallelogram.
Triangles on the same base (or equal bases) and between the same parallels are equal in area.
Area of a triangle is half the product of its base and the corresponding altitude.
A median of a triangle divides it into two triangles of equal areas