1. The perpendicular from the centre of a circle to a chord bisects the chord.

2. There is one and only one circle passing through three non-collinear points.

3. If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major)are congruent.

4. Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

5. The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.




6. The sum of either pair of opposite angles of a cyclic quadrilateral is 180°

7. Heron's formula for calculating the Area of a triangle.
   Area of triangle = √s(s-a)(s-b)(s-c)

8. s = semi-perimeter of triangle = (a+b+c) / 2

9. Area of a quadrilateral whose sides and one diagonal are given, can be calculated by dividing the quadrilateral into two triangles and using the Heron’s formula.

10. Surface area of a cuboid = 2(lb + bh + hl )

11. Surface Area of a Cube = 6a²

12. Lateral surface area of a cuboid of length l, breadth b and height h is equal to 2lh + 2bh or 2(l + b)h.

13. Lateral surface area of a cube of side a is equal to 4a²

14. Curved Surface Area of a Cylinder = 2πrh

15. Total Surface Area of a Cylinder = 2πr(r + h); where h is the height of the cylinder and r its radius.

16. Curved surface area of a cone = πrl

17. Total surface area of a right circular cone = πrl + πr² i.e., πr ( l + r)




18. Surface area of a sphere of radius r = 4 π r²

19. Curved surface area of a hemisphere = 2πr²

20. Total surface area of a hemisphere = 3πr²

21. Volume of a cuboid = l × b × h

22. Volume of a cube = a³

23. Volume of a cylinder = πr²h

24. Volume of a cone = (1/3) * πr²h

25. Volume of a sphere of radius r = (4/3) * πr³

26. Volume of a hemisphere of radius r = (2/3) * πr³

Q. Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden box covered with coloured paper with picture of Santa Claus on it. She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively how many square sheets of paper of side 40 cm would she require?

1. The quantity of paper required would be equal to the surface area of the box which is of the shape of a cuboid. The dimensions of the box are: Length =80 cm, Breadth = 40 cm, Height = 20 cm.

2. The surface area of the box = 2(lb + bh + hl) = 11200 sq cm

3. The area of each sheet of the paper = 40 × 40 sq. cm

4. Therefore, number of sheets required = (surface area of box) / (area of one sheet of paper) = 11200/1600

Ans.7

Q.Hameed has built a cubical water tank with lid for his house, with each outer edge 1.5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm . Find how much he would spend for the tiles, if the cost of the tiles is Rs. 360 per dozen.

1. Edge of the cubical tank = 1.5 m = 150 cm (= a)

2. Surface area of the tank = 5 × 150 × 150 sq. cm

3. Area of each square tile = side × side = 25 × 25 sq. cm

4. Number of tiles required = (surface area of box) / (area of one sheet of paper) = 180

5. Cost of 1 dozen tiles, i.e., cost of 12 tiles = Rs. 360

6. Therefore, cost of one tile = Rs 360 / 12 = Rs 30

7. So, the cost of 180 tiles = 180 × Rs 30 = Rs 5400

Ans.5400

1. Mean : It is found by adding all the values of the observations and dividing it by the total number of observations. It is denoted by x .



2. Median : It is the value of the middle-most observation (s).If n is an odd number, the median = value of the (n+1/2)th observation. If n is an even number, median = Mean of the values of the n/2 and (n+1/2)th observation.

3. Mode : The mode is the most frequently occurring observation.

1. If we are tossing a coin and calculating the probability of getting heads then each toss is a trial.

2. The getting of a head in a particular throw is an event with outcome 'head'. Similarly, getting a tail is an event with outcome 'tail'.

3. The probability of each event lies between 0 and 1 (0 and 1 inclusive)

4. Let n be the total number of trials. The empirical probability P(E) of an event E happening, is given by P(E) = (Number of trials in which the event happened)/ (The total number of trials)

5. The sum of all the probabilities is 1.

Q.An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table

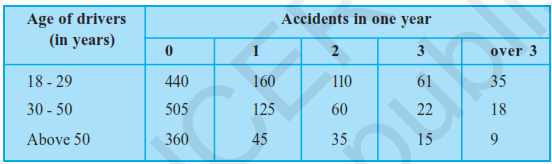
Find the probabilities of the following events for a driver chosen at random from the city:
(i) being 18-29 years of age and having exactly 3 accidents in one year.
(ii) being 30-50 years of age and having one or more accidents in a year.
(iii) having no accidents in one year.

1. Total number of drivers = 2000.

2. The number of drivers who are 18-29 years old and have exactly 3 accidents in one year is 61.

3. So, P (driver is 18-29 years old with exactly 3 accidents) = 61/2000 = 0.031

4. The number of drivers 30-50 years of age and having one or more accidents in one year = 125 + 60 + 22 + 18 = 225 So, P(driver is 30-50 years of age and having one or more accidents) = 225/2000 = 0.113

5. The number of drivers having no accidents in one year = 440 + 505 + 360 = 1305

Previous

Next