Arithmetic Progressions
An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term. This fixed number is called the common difference of the AP. Remember that it can be positive, negative or zero.
Let us denote the first term of an AP by a1, second term by a2, . . ., nth term by an and the common difference by d. Then the AP becomes a1, a2, a3, . . ., an
Therefore a2 - a1 = a3 - a2 = an - a n-1 = d
The nth term an of the AP with first term a and common difference d is given by an = a + ( n - 1 )*d .
S = n / 2 * [2a + (n – 1) d ] , where S = Sum of first 'n' terms in A.P with first term = a and common difference = d.
S = n / 2 * [a + an ]
The nth term of an AP is the difference of the sum to first n terms and the sum to first (n – 1) terms of it, i.e., an = Sn - Sn-1
The sum of first n positive integers is given by Sn = n ( n + 1 ) / 2
If a, b, c are in AP, then b = ( a + c ) / 2 and b is called the arithmetic mean of a and c.
Arithmetic Progressions Problems
Q. Find the 11th term from the last term (towards the first term) of the AP : 10, 7, 4, . . ., – 62.
Here, a = 10, d = 7 – 10 = – 3, l = – 62, where last term be denoted by 'l'.
l = a + (n – 1) d
To find the 11th term from the last term, we will find the total number of terms in the AP.
a 11 = – 62 = 10 + (n – 1)(–3)
n = 25
The 11th term from the last term will be the 15th term.
a15 = 10 + (15 – 1)(–3) = 10 – 42 = – 32
Alternatively : If we write the given AP in the reverse order, then a = – 62 and d = 3 So, the question now becomes finding the 11th term with these a and d
a 11 = – 62 + (11 – 1) × 3 = – 62 + 30 = – 32
Ans . - 32
Geometry
If corresponding angles of two triangles are equal, then they are known as equiangular triangles.
The ratio of any two corresponding sides in two equiangular triangles is always the same.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar.
If in two triangles, sides of one triangle are propor tional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similiar.
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are propor tional, then the two triangles are similar.
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides
The distance between P ( x1 , y1 ) and P ( x2 , y2 ) is √ (x2 - x1)2 + (y2 - y1)2
The distance of a point P(x, y) from the origin is √ (x2 + y2)
The coordinates of the point P(x, y) which divides the line segment joining the points is A(x1 , y1) and B(x2 , y2 ) internally in the ratio m1 : m2 are
The mid-point of the line segment joining the points P ( x1 , y1 ) and Q ( x2 , y2 )
The area of the triangle formed by the points P ( x1 , y1 ) and Q ( x2 , y2 ) and R ( x3 , y3 ) is
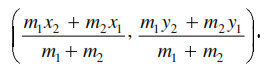
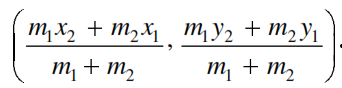
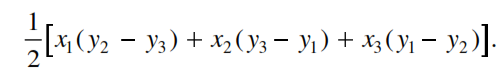
Trigonometry
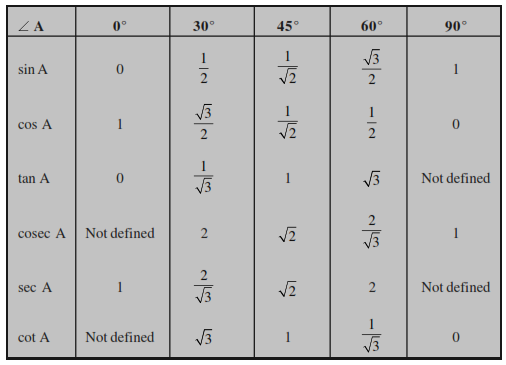
sine of ∠ A = side opposite to angle A / hypotenuse
cosine of ∠ A = side adjacent to angle A / hypotenuse
tangent of ∠ A = side opposite to angle A / side adjacent to angle A
cosecant of ∠ A = hypotenuse / side opposite to angle A
secant of ∠ A = hypotenuse / side adjacent to angle A
cotangent of ∠ A = side adjacent to angle A / side opposite to angle A
The ratios defined above are abbreviated as sin A, cos A, tan A, cosec A, sec A and cot A respectively. Note that the ratios cosec A, sec A and cot A are respectively, the reciprocals of the ratios sin A, cos A and tan A.
Trigonometric Formulae
sin (90° – A) = cos A
cos (90° – A) = sin A
tan (90° – A) = cot A
cot (90° – A) = tan A
sec (90° – A) = cosec A
cosec (90° – A) = sec A
Perimeter and Area of a Circle
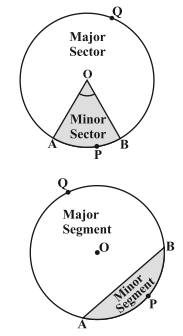
Portion (or part) of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle and the portion (or part) of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.
Area of a sector of a circle of angle θ, length of an arc of a sector of angle θ =
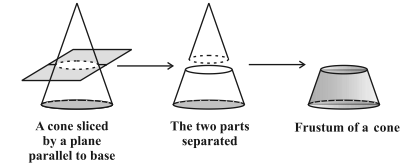
Frustum of a cone = Given a cone, when we slice (or cut) through it with a plane parallel to its base and remove the cone that is formed on one side of that plane, the part that is now left over on the other side of the plane is called a frustum of the cone.
Let h be the height, l the slant height and r 1 and r2 the radii of the ends such that r 1 > r2 of the frustum of a cone. Then we can directly find the volume, the curved surface area and the total surface area of frustum by using the formulae given below :
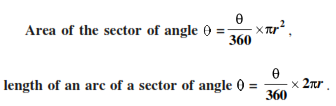
Formulae for calculating the Volume of the frustum of the cone, the curved surface area of the frustum of the cone and Total surface area of the frustum of the cone
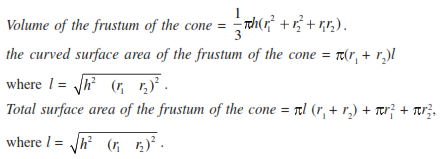
Probability
The sum of the probabilities of all the elementary events of an experiment is 1
P(E) = ( Number of outcomes favourable to E ) / ( Number of all possible outcomes of the experiment )
P(E) = 1 – P(E)
Probability of an event which is impossible to occur is 0
Probability of an event which is sure (or certain) to occur is 1.