SETS
N: the set of all natural numbers
Z:the set of all integers
Q:the set of all rational numbers
R:the set of real numbers
Z+ : the set of positive integers
Q+ : the set of positive rational numbers
R+ : the set of positive real numbers.
Given two sets A and B, if every element of A is also an element of B and if every element of B is also an element of A
A set A is said to be a subset of a set B if every element of A is also an element of B. A ⊂ B.
A ⊂ B and B ⊂ A ⇔ A = B
every set A is a subset of itself, i.e., A ⊂ A. Since the empty set Φ has no elements, we agree to say that Φ is a subset of every set.
Power Set P(A) : Consider the set {1, 2}. Let us write down all the subsets of the set {1, 2}. We know that Φ is a subset of every set . So, Φ is a subset of {1, 2}. We see that {1} and { 2 }are also subsets of {1, 2}. Also, we know that every set is a subset of itself. So, { 1, 2 } is a subset of {1, 2}. Thus, the set { 1, 2 } has, in all, four subsets, viz. Φ, { 1 }, { 2 } and { 1, 2 }. The set of all these subsets is called the power set of {1, 2}.
The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as "A minus B".
SETS Laws:
(A ∪ B)' = A' ∩ B' and ( A ∩ B )' = A' ∪ B'
n (A ∪ B) = n (A) + n (B) – n (A ∪ B)
n ( A ∪ B ∪ C ) = n (A) + n ( B ) + n ( C ) – n ( A ∩ B ) – n ( B ∩ C) – n ( A ∩ C ) + n ( A ∩ B ∩ C )
A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C )
( A ∩ B ) ∩ C = A ∩ ( B ∩ C )
RELATIONS AND FUNCTIONS:
Relation A relation R from a set A to a set B is a subset of the cartesian product A * B obtained by describing a relationship between the first element x and the second element y of the ordered pairs in A * B.
The image of an element x under a relation R is given by y, where (x, y) ∈ R
The domain of R is the set of all first elements of the ordered pairs in a relation R.
The range of the relation R is the set of all second elements of the ordered pairs in a relation R.
Function A function f from a set A to a set B is a specific type of relation for which every element x of set A has one and only one image y in set B. We write f: A -> B, where f(x) = y.
A is the domain and B is the codomain of f.
The range of the function is the set of images.
A real function has the set of real numbers or one of its subsets both as its domain and as its range.
Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal.
If there are p elements in A and q elements in B, then there will be pq elements in A * B, i.e., if n(A) = p and n(B) = q, then n(A * B) = pq.
The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A * B. If n(A ) = p and n(B) = q, then n (A * B) = pq and the total number of relations is 2pq .
Algebra of functions
For functions f : X -> R and g : X -> R, we have
(f + g) (x) = f(x) + g(x), x ∈ X.
(f – g) (x) = f (x) – g(x), x ∈ X.
(f.g) (x) = f (x) .g (x), x ∈ X.
(kf) (x) = k f (x) ), x ∈ X.
(f/g)(x) = f(x) / g(x) , x ∈ X and g(x) ≠ 0
Trigonometry
If in a circle of radius r, an arc of length l subtends and angle of θ radians, then : l = r θ
Radian measure = ( π / 180 ) * Degree measure
Degree measure = ( 180 / π ) * Radian measure
cos2x + sin2x = 1
1 + tan2x = sec2x
1 + cot2x = cosec2x
cos (2nπ + x) = cos x
sin (2nπ + x) = sin x
sin (– x) = – sin x
cos (– x) = cos x
cos (x + y) = cos x cos y – sin x sin y
cos (x – y) = cos x cos y + sin x sin y
cos (π / 2 - x) = sin x
sin (π / 2 - x) = cos x
sin (x + y) = sin x cos y + cos x sin y
sin (x – y) = sin x cos y – cos x sin y
cos (π / 2 + x) = - sin x
sin (π / 2 + x) = cos x
cos (π – x) = – cos x
sin (π – x) = sin x
cos (π + x) = – cos x
sin (π + x) = – sin x
cos (2π – x) = cos x
sin (2π – x) = – sin x
If none of the angles x, y and (x ± y) is an odd multiple of (π /2) then
If none of the angles x, y and (x ± y) is a multiple of π, then
cos 2x = cos2x - sin2x = 2cos2x-1 = 1 - 2sin2x = (1-tan2x)/(1+tan2x)
sin 2x = 2 sin x * cos x
tan x = tan y implies x = n*π + y, where n ∈ Z.
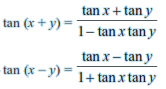
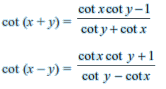

Complex Numbers and Quadratic Equations
A number of the form a + ib, where a and b are real numbers, is called a complex number, a is called the real part and b is called the imaginary part of the complex number.
Let z1 = a + ib and z2 = c + id. Then
z1 + z2 = (a + c) + i (b + d)
z1 * z2 = (ac – bd) + i (ad + bc)
For any non-zero complex number z = a + ib (a ≠ 0, b ≠ 0), there exists the complex number
\frac{a}{a^2 + b^2} + i\frac{-b}{a^2 + b^2}denoted by\frac{1}{z} or z^{-1}called multiplicative inverse of z such thatz * \frac{1}{z}=1For any integer k, $i^{4k}$ = 1 , $i^{4k+1}$ = i, $i^{4k+2}$ = -1, $i^{4k+3}$ = -i
The conjugate of the complex number z = a + ib, denoted by z is given by z = a – ib.
The polar form of the complex number z = x + iy is r (cosθ + i sinθ), where r = $\sqrt{x^2 + y^2}$ (the modulus of z) and cosθ = $\frac{x}{r}$ and sinθ = $\frac{y}{r}$. (θ is known as the argument of z. The value of θ, such that – π < θ ≤ π , is called the principal argument of z.
A polynomial equation of n degree has n roots.
The solutions of the quadratic equation ax2 + bx + c = 0; where a, b, c ∈ R and a ≠ 0 ; b2 – 4ac < 0 , are given by x = $\frac{-b\pm\sqrt{4ac - b^2*i}}{2a}$
LINEAR INEQUALITIES
Two real numbers or two algebraic expressions related by the symbols <, >, ≤ or ≥ form an inequality.
Equal numbers may be added to (or subtracted from ) both sides of an inequality.
Both sides of an inequality can be multiplied (or divided ) by the same positive number. But when both sides are multiplied (or divided) by a negative number, then the inequality is reversed.
The values of x, which make an inequality a true statement, are called solutions of the inequality
To represent x < a (or x > a) on a number line, put a circle on the number a and dark line to the left (or right) of the number a.
To represent x ≤ a (or x ≥ a) on a number line, put a dark circle on the number a and dark the line to the left (or right) of the number x.
If an inequality is having ≤ or ≥ symbol, then the points on the line are also included in the solutions of the inequality and the graph of the inequality lies left (below) or right (above) of the graph of the equality represented by dark line that satisfies an arbitrary point in that part.
If an inequality is having < or > symbol, then the points on the line are not included in the solutions of the inequality and the graph of the inequality lies to the left (below) or right (above) of the graph of the corresponding equality represented by dotted line that satisfies an arbitrary point in that part.
The solution region of a system of inequalities is the region which satisfies all the given inequalities in the system simultaneously.
PERMUTATIONS AND COMBINATIONS
Fundamental principle of counting If an event can occur in m different ways, following which another event can occur in n different ways, then the total number of occurrence of the events in the given order is m * n.
The number of permutations of n different things taken r at a time, where repetition is not allowed, is denoted by nPr and is given by nPr = $\frac{n!}{(n-r)!}$ where 0 ≤ r ≤ n.
n! = 1 * 2 * 3 * ...* n
n! = n × (n – 1) !
The number of permutations of n different things, taken r at a time, where repetition is allowed, is nr
The number of permutations of n objects taken all at a time, where p1 objects are of first kind, P2 objects are of the second kind, ..., Pk objects are of the kth kind and rest, if any, are all different is $\frac{n!}{p_1! * p_2! * ... * p_k!}$
The number of combinations of n different things taken r at a time, denoted by nCr is given by nCr = $\frac{n!}{r!(n-r)!}$, 0 ≤ r ≤ n.