SEQUENCES AND SERIES
By a sequence, we mean an arrangement of a number in a definite order according to some rule. Also, we define a sequence as a function whose domain is the set of natural numbers or some subsets of the type {1, 2, 3....k). A sequence containing a finite number of terms is called a finite sequence. A sequence is called infinite if it is not a finite sequence.
Let a1 , a2 , a3... be the sequence, then the sum expressed as a1 + a2 + a3 +... is called series. A series is called finite series if it has got finite number of terms.
An arithmetic progression (A.P.) is a sequence in which terms increase or decrease regularly by the same constant. This constant is called common difference of the A.P. Usually, we denote the first terms of A.P. by a, the common difference by d and the last term by l. The general term or the n term of the A.P. is given by a = a + (n – 1) d.
The sum $S_n$ of the first n terms of an A.P. is given by $S_n = \frac{n}{2} [ 2a + (n-1)d ]$ = $S_n = \frac{n}{2} [ a + l ]$
The arithmetic mean A of any two numbers a and b is given by $\frac{a+b}{2}$ i.e., the sequence a, A, b is in A.P.
A sequence is said to be a geometric progression or G. P. , if the ratio of any term to its preceding term is same throughout. This constant factor is called the common ratio. Usually, we denote the first term of a G.P. by a and its common ratio by r. The general or the $n^{th}$ term of G.P. is given by $a_n = a*r^{n-1}$
The sum $S_n$ of the first n terms of G.P. is given by $S_n = \frac{a(r^n - 1)}{r - 1}$ or $S_n = \frac{a( 1 - r^n)}{1 - r}$ if r ≠ 1
The geometric mean (G.M.) of any two positive numbers a and b is given by $\sqrt{ab}$ i.e., the sequence a, G, b i s G. P.
STRAIGHT LINES
Slope (m) of a non-vertical line passing through the points $(x_1, x_2)$ and $(y_1, y_2)$ is given by m = $\frac{y_2 - y_1}{x_2 - x_1}$ = $\frac{y_1 - y_2}{x_1 - x_2}$ , $x_1$ ≠ $x_2$
If a line makes an angle α with the positive direction of x-axis, then the slope of the line is given by m = tan α, α ≠ 90°.
Slope of horizontal line is zero and slope of vertical line is undefined.
Two lines are parallel if and only if their slopes are equal.
Two lines are perpendicular if and only if product of their slopes is –1.
Three points A, B and C are collinear, if and only if slope of AB = slope of BC.
Equation of the horizontal line having distance a from the x-axis is either y = a or y = – a.
Equation of the vertical line having distance b from the y-axis is either x = b or x = – b.
The point (x, y) on the line with slope m and y-intercept c lies on the line if and only if y = mx + c.
If a line with slope m makes x-intercept d. Then equation of the line is y = m (x – d).
Any equation of the form Ax + By + C = 0, with A and B are not zero, simultaneously, is called the general linear equation or general equation of a line.
The equation of the line having normal distance from origin p and angle between normal and the positive x-axis ω is given by xcosω + ysinω = p
An acute angle (say θ) between lines $L_1$ , $L_2$ and slope $m_1$ , $m_2$ is given by tan ω = $\frac{|m_2 - m_1|}{|1 + m_1*m_2|}$ if $1 + m_1*m_2$ ≠ 0
The point (x, y) lies on the line with slope m and through the fixed point ($x_0, y_0$), if and only if its coordinates satisfy the equation $y$ – $y_0$ = m (x – $x_0$).
Equation of the line passing through the points $(x_1, x_2)$ and $(y_1, y_2)$ is given by $y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1)$
Equation of a line making intercepts a and b on the x-and y-axis, respectively, is $\frac{x}{a}$ + $\frac{y}{b}$ = 1
The perpendicular distance (d) of a line Ax + By+ C = 0 from a point $(x_1, y_1)$ is given by d = $\frac{|Ax_1+By_1+C|}{\sqrt{A^2 + B^2}}$
Distance between the parallel lines Ax + By+ $C_1$ = 0 and Ax + By+ $C_2$ = 0 is given by d = $\frac{|C_1 - C_2|}{\sqrt{A^2 + B^2}}$
CONIC SECTIONS
A circle is the set of all points in a plane that are equidistant from a fixed point in the plane.
The equation of a circle with centre (h, k) and the radius r is $(x-h)^2 + (y-k)^2 = r^2$
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point in the plane
The equation of the parabola with focus at (a, 0) a > 0 and directrix x = – a is $y^2 = 4ax$
Length of the latus rectum of the parabola $y^2 = 4ax$ is 4a.
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane is a constant.
The equations of an ellipse with foci on the x-axis is $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
Latus rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose end points lie on the ellipse.
Length of the latus rectum of the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ is $\frac{2b^2}{a}$
The eccentricity of an ellipse is the ratio between the distances from the centre of the ellipse to one of the foci and to one of the vertices of the ellipse
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane is a constant.
The equation of a hyperbola with foci on the x-axis is $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$
Latus rectum of hyperbola is a line segment perpendicular to the transverse axis through any of the foci and whose end points lie on the hyperbola.
Length of the latus rectum of the hyperbola : $\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ is : $\frac{2b^2}{a}$
The eccentricity of a hyperbola is the ratio of the distances from the centre of the hyperbola to one of the foci and to one of the vertices of the hyperbola.
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
In three dimensions, the coordinate axes of a rectangular Cartesian coordinate system are three mutually perpendicular lines. The axes are called the x, y and z-axes.
The three planes determined by the pair of axes are the coordinate planes, called XY, YZ and ZX-planes.
The three coordinate planes divide the space into eight parts known as octants.
The coordinates of a point P in three dimensional geometry is always written in the form of triplet like (x, y, z). Here x, y and z are the distances from the YZ, ZX and XY-planes.
Any point on x-axis is of the form (x, 0, 0)
Any point on y-axis is of the form (0, y, 0)
Any point on z-axis is of the form (0, 0, z).
Distance between two points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ is given by $PQ = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$
The coordinates of the point R which divides the line segment joining two points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ internally and externally in the ratio m : n are given by $( \frac{mx_2 + nx_1}{m+n},\frac{my_2 + ny_1}{m+n},\frac{mz_2 + nz_1}{m+n} )$ respectively.
The coordinates of the mid-point of the line segment joining two points $P(x_1,y_1,z_1)$ and $Q(x_2,y_2,z_2)$ are $ (\frac{x_2 + x_1}{2},\frac{y_2 + y_1}{2},\frac{z_2 + z_1}{2} ) $
The coordinates of the centroid of the triangle, whose vertices are $P(x_1,y_1,z_1)$ , $Q(x_2,y_2,z_2)$ and $R(x_3,y_3,z_3)$ are $ (\frac{x_3 + x_2 + x_1}{3},\frac{y_3 + y_2 + y_1}{3},\frac{z_3 + z_2 + z_1}{3} ) $
BINOMIAL THEOREM
The expansion of a binomial for any positive integral n is given by Binomial Theorem, which is
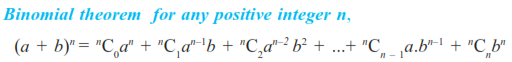
PROBABILITY
Sample space: The set of all possible outcomes
Sample points: Elements of sample space
Event: A subset of the sample space
Impossible event : The empty set
Sure event: The whole sample space
Complementary event or 'not event' : The set A' or S – A
Event A or B: The set A ∪ B
Event A and B: The set A ∩ B
Event A and not B: The set A – B
Mutually exclusive event: A and B are mutually exclusive if A ∩ B = φ
Exhaustive and mutually exclusive events: Events $E_1$ , $E_2$ , ... , $E_n$ are mutually exclusive and exhaustive if $E_1$ ∪ $E_2$ ∪ , ... ,∪ $E_n$ = S and $E_i$ ∩ $E_j$ = φ
Equally likely outcomes: All outcomes with equal probability
Probability of an event: For a finite sample space with equally likely outcomes Probability of an event P(A) = $\frac{n(A)}{n(S)}$ ; where n(A) = number of elements in the set A, n(S) = number of elements in the set S.
If A and B are any two events, then P(A or B) = P(A) + P(B) – P(A and B) equivalently, P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
If A and B are mutually exclusive, then P(A or B) = P(A) + P(B)
If A is any event, then P(not A) = 1 – P(A)
STATISTICS
Measures of dispersion Range, Quartile deviation, mean deviation, variance, standard deviation are measures of dispersion. Range = Maximum Value – Minimum Value
Mean deviation for ungrouped data
M.D. $\overline{x} = \frac{\sum(x_i - \overline{x})}{n}$
M.D. M = $\frac{\sum(x_i - M)}{n}$
Variance and standard deviation for ungrouped data
$\sigma^2 = \frac{1}{n} \sum (x_i - \overline{x})^2$
$\sigma = \sqrt{ \frac{1}{n} \sum (x_i - \overline{x})^2 }$
Mean deviation for grouped data
M.D. $\overline{x} = \frac{\sum f_i(x_i - \overline{x})}{n}$
M.D. M = $\frac{\sum f_i(x_i - M)}{n}$ , where N = $\sum f_i$
