Section 4:Past Years' Solved Questions from the SNAP
5.SNAP 2007
Ans .
(a) 
- Explanation :
Since all labels are wrong, the box labeled GOLD OR SILVER would have neither gold nor silver. Thus, it would have bronze. Consequently, the chest marked GOLD, would have silver in it and the chest marked SILVER, would have gold in it. Thus, we do not need to open any chest in order to find out which chest has which coins. Thus, option (a) is correct.
Ans .
(b) 93
- Explanation :
27 minutes past 10 AM is 93 minutes before 12 noon. Option (b) is correct.
Directions for Questions 3 and 5: Read the following passage and answer the questions. An employee has been assigned the task of allotting offices to six of the staff members. The offices are numbered 1-6. The offices are arranged in a row and they are separated from each other by six foot high dividers. Hence voices, sounds and cigarette smoke flow easily from one office to another. Miss Ruby needs to use the telephone quite often throughout the day. Mr. Minhas and Mr. Brar need adjacent offices as they need to consult each other often while working. Miss Harsha is a senior employee and has to be allotted the office number 5, having the biggest window. Mr. Dongre requires silence in the offices next to his. Mr. Tanjore, Mr. Minhas and Mr. Dongre are all smokers. Miss Harsha finds tobacco smoke allergic and consequently the offices next to hers are to be occupied by non-smokers. Unless specifically stated all the employees maintain an atmosphere of silence during office hours.
- Explanation :
The starting grid would look as follows:
 We first place Miss Harsha in the 5th office. The grid would become:
We first place Miss Harsha in the 5th office. The grid would become:
 The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
 We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
 Option (d) is correct
Option (d) is correct
- Explanation :
The starting grid would look as follows:
 We first place Miss Harsha in the 5th office. The grid would become:
We first place Miss Harsha in the 5th office. The grid would become:
 The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
 We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
 Option (d) is correct
Option (d) is correct
- Explanation :
The starting grid would look as follows:
 We first place Miss Harsha in the 5th office. The grid would become:
We first place Miss Harsha in the 5th office. The grid would become:
 The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
The other people are: Ruby (telephone use throughout the day), Minhas-Brar (together and need to
discuss), Dongre (needs silence) and Tanjore.
Also, Tanjore, Minhas and Dongre being smokers they would not occupy the 4th or the 6th cabin.
Also, Brar cannot occupy the 6th cabin as he needs to be with Minhas.
This leaves us with only Ruby to occupy the 6th office. Also, Brar being the only other non-smoker he
would need to be put into the 4th cabin, and Minhas obviously has to be his neighbor.
The grid would become:
 We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
We are just left to place Tanjore and Dongre now. Dongre needs to have silence and hence he cannot
be put in the 2nd cabin next to Minhas (as Minhas would be continuously discussing with Brar
throughout the day).
Thus, Dongre would take the 1st cabin and hence, Tanjore would take the 2nd cabin.
The grid would end up as:
 Option (d) is correct
Option (d) is correct
Ans .
(d) Mr. Dongre
Ans .
(d) 1, 2 and 3
Ans .
(d) Mr. Tanjore taking over the duties formerly taken care of by Miss Ruby.
Ans .
(b) They must either both be appointed or both be left out.
- Explanation :
Since Shankar and Jwala both 'refuse to work with each other' it obviously means that either.
Ans .
(c) The two totals need not be equal.
- Explanation :
The obvious answer in this case is that both the totals need not be equal. For example, if he had withdrawn ` 100 in the first case, the columns would look like:
 Hence, option (c) is the correct answer
Hence, option (c) is the correct answer
Ans .
(d) 5
- Explanation :
In each row, there is one figure with two legs, one with three legs and one with 4 legs. Hence, the third figure in the bottom row should have 2 legs. This leaves us between figures 2 and 5. The other thing you can notice in the first two rows is that of the three figures, only one figure has flat bottom extensions to some or all of their legs. In the third row, the second figure has already used flat bottom extensions to the legs in the second figure of the row. Thus, the figure, which would replace the question mark would not have flat bottom extensions. Thus, we need figure 5 amongst those shown to replace the question mark. Thus, option (d) is correct.
Ans .
(c) 3
- Explanation :
The right side of the first figure in the two-figure analogy is replaced by a two-sided angle kind of structure. The third figure gives us the same relationship. Option (c) is correct
Ans .
(c) D
- Explanation :
In the pattern of the five figures shown, the dark quarter of the figure is rotating in a clockwise fashion. Thus, in the missing figure the dark quarter should be at the bottom right. Figure (d) gives us that. Hence, option (c) is correct
Directions for Questions 11 and 13: These questions are based on the following information. During their school Silver Jubilee Reunion, four alumni were discussing their starting annual salaries back in 1981. The salaries in question were Rupees 40, 50, 60 and 70 thousand per year. Of course the present MD of a private company earned the most. Arvind earned more than Biswajeet, and the doctor earned more than Dhruv the engineer. Chinmay could not remember what he started on. Biswajeet the lawyer did not start on 50,000, nor did Dhruv.
- Explanation :
The starting grid in this case would be:
 The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
 At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
 From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
 The answers can then be read off the above table. Chinmay is a doctor. Option (c) is correct.
The answers can then be read off the above table. Chinmay is a doctor. Option (c) is correct.
- Explanation :
The starting grid in this case would be:
 The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
 At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
 From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
 The answers can then be read off the above table.
The lwayer started at ` 60000. Option (c) is correct.
The answers can then be read off the above table.
The lwayer started at ` 60000. Option (c) is correct. - Explanation :
The starting grid in this case would be:
 The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
The four persons are: Arvind, Biswajeet (lawyer), Chinmay, Dhruv (engineer). This leaves us
with two professions, which have not been fixed with the respective persons. Between Arvind
and Chinmay the professions of doctor and MD are to be shared.
Since, the lawyer and the engineer did not start on 50000 (which is evident from the statement
'Biswajeet the lawyer did not start on ` 50000 nor did Dhruv) it must be the doctor who
started with 50000. The grid becomes:
 At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
At this point, the statement "the doctor earned more than Dhruv the engineer" becomes usable
in the grid and can be put into the grid. The engineer would become the person with 40000
starting salary and obviously then the lawyer would be starting with 60000.
The grid would then become
 From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
From this point, if we use that Arivnd > Biswajeet we know that Arvind is the MD. The final
solution grid becomes:
 The answers can then be read off the above table.
Arvind received the highest starting salary. Option (a) is correct.
The answers can then be read off the above table.
Arvind received the highest starting salary. Option (a) is correct.
Ans .
(c) Doctor
Ans .
(c) 60,000
Ans .
(a) Arvind
Ans .
(b) Wednesday
- Explanation :
The first rest day would be on the next Tuesday and can be visualised as:
 The second round of work would start on Wednesday and end on the next Wednesday and
consequently, the next rest day would be on a Thursday.
The respective rest days can be visualised as below:
The second round of work would start on Wednesday and end on the next Wednesday and
consequently, the next rest day would be on a Thursday.
The respective rest days can be visualised as below:
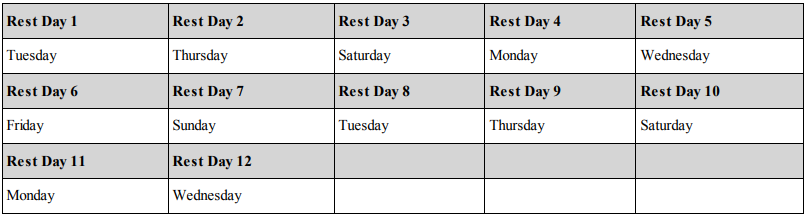 Option (b) is the correct answer.
Option (b) is the correct answer.
Ans .
(b) 2, 3, 7
- Explanation :
Figures 2, 3 and 7 are rotated in a opposite direction to the figures 1, 4, 5 and 6. Thus, these figures are the odd ones out. Option (b) is correct
Ans .
(a) Snehal, Waman, Tanmay.
- Explanation :
If we consider the two statements that Babloo has made, it is clearly evident that his first statement cannot be true. Because, if his first statement "Tanmay won the race" were true, then Bunty's second statement "Tanmay came second" is false. Then, Bunty's first statement "It was Snehal who won" must be correct; but it cannot be correct since, if Bunty won the race, then Snehal cannot come first. In such an event, if we were to consider Babloo's first statement to be true, both of Bunty's statements would be false - which goes against the basic condition of the question. Hence, Babloo's second statement "Waman came second" must be true. Then Bunty's second statement "Tanmay came second" is naturally false and hence Bunty's first statement "It was Snehal who won" must be true. So, Snehal came first, Waman came second and Tanmay came third. Option (a) is correct
Ans .
(b) 6
- Explanation :
The routes can be counted as: P-1-4-Q; P-1-5-Q; P-3-5-Q; P-3-4-Q; P-2-4-Q; P-2-5-Q Thus, there are a total of 6 routes from P to Q. Option (b) is the correct answer
Ans .
(a) A
- Explanation :
The word formed by using the letters in the circle B is: SCANTY. In Circle C: SECANT and in Circle D: CHEATS. Only the letters of Circle A do not form a complete word if all the six letters are used. Option (a) is correct.
Ans .
(b) 10
- Explanation :
The total of all the numbers given to us would be given by: (Sum of numbers listed separately in the question) + (Numbers already placed in the grid) = (2 + 3 + 4 + 5 + 7 + 10 + 11 + 12 + 13) + (1 + 9 +14 + 15) = 106. The number that should be left out should be such that after it's removal, the sum of all other remaining numbers should be divisible by 3 as well as by 4. This is because, we need to have the total sum of the remaining numbers such that it can be divided into three equal integral elements (for the rows). Besides, this number should also be possibly divisible into four equal integral elements (for the columns). Looking at the options, if we check for option (a): Leaving out the digit 4, leaves us with a sum of 102 for the remaining 12 numbers. This can be divided into 3 rows summing up to 34 each. However, we cannot break up 102 into 4 equal integral parts and hence we cannot leave out 4 and achieve the desired result. If we check for option (b): Leaving out the number 10, leaves us with a sum of 96 for the remaining 12 numbers. This can be divided into 3 rows summing up to 32 each. Besides, 96 can also be broken up into 4 equal integral parts of 24 each. If we check for option (c), it gets rejected based on the following thinking: Leaving out the number 15, leaves us with a sum of 91 for the remaining 12 numbers. This cannot be divided into 3 equal integral values for each row. Hence, this option is obviously wrong. If we check for option (d): Leaving out the number 7, leaves us with a sum of 99 for the remaining 12 numbers. This can be divided into 3 rows summing up to 33 each. However, we cannot break up 99 into 4 equal integral parts and hence we cannot leave out 7 and achieve the desired result. Thus, only option (b) is feasible and is the correct answer.
Ans .
(b) 18
- Explanation :
In this case, the product of the last two numbers in every set of 4 numbers, is double the product of the first two numbers. Thus, in the first set: 12 ¥ 8 = 2 ¥ (6 ¥ 8); In the second set: 6 ¥ 10 = 2 ¥ (5 ¥ 6); In the third set: 4 ¥ ? = 2 ¥ (3 ¥ 12) Æ the number in place of the question mark should be 18. Hence option (b) is correct.
Ans .
(b) Below
- Explanation :
The series of alphabets is: A (below) - BCDE (above) - FGHI (below) - JKLM (above) - NOPQ (below) - RSTU (above) - VWXY (below) Hence, W should be placed below. Option (b) is correct
Ans .
(d) 7
- Explanation :
The following family structure would give the required relations:
In this case the following holds: 1 Grandfather = X; 1 Grandmother = Y; Two Fathers = X and Z; Two Mothers = A and Y; Four Children = Z, B, C and D; Three grand children = B, C and D; One brother = B; Two Sisters = C and D; Two Sons = Z and B; Two daughters = C and D; One father-in-law = X; One Mother-in-law = Y One daughter-in-law = A. In this case there are only seven people required to fulfill all conditions specified by the problem. These are (X, Y, Z, A, B, C and D) Thus, there are 7 people in the family. Option (d) is correct.
Ans .
(a) Operator gets a profit of 6% on each Rupee bet
- Explanation :
In such cases, the operator always wins and the only option that satisfies this condition is option (a). Options (b) and (c) cannot be correct because they talk about the operator suffering a loss-which would not be true in an operator defined and controlled game. Hence, these options can be rejected. Option (d) is also rejected because whether the player wins or loses will change with every throw of the die and depends on the actual outcome of the throw. Option (a) is correct.
Ans .
(b) 30
- Explanation :
If he got 30, his spends would be: First store = 16; Money left = 14; Second store = 8; Money left = 6 Third store = 4; Money left = 2; Fourth store = 2; Money left = 0. Thus, option (b) is correct.
Ans .
(d) Only (jc) follows.
- Explanation :
If some wise men are extrovert, then it necessarily follows that some extrovert are wise men. Thus, (jc) is definitely correct as a conclusion. Conclusion (ja) is not necessarily true and neither is (jb) necessarily true. Option (d) is correct.
Directions for Questions 26 and 28: Use the data given below to answer the questions. The following are the results of a survey conducted on a small cross-section of students from Symbiosis Group of institutes, to determine the readership of three magazines. This survey was conducted in Dec. 2006. S Number of students who read only Business India was 40 S 60 students read only Outlook S 110 students read only India Today S 30 students read all the three magazines S 20 read Business India and India Today, but not Outlook S 50 read Business India and Outlook, but not India Today S 40 read Outlook and India Today, but not Business India
- Explanation :
The following Venn diagram would give us the overall structure of the numbers involved in this situation:
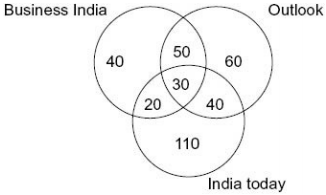 The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
Option (b) is correct.
The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
Option (b) is correct. - Explanation :
The following Venn diagram would give us the overall structure of the numbers involved in this situation:
 The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
110 + 40 + 60 = 210 students did not read Business India. Option (d) is correct
The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
110 + 40 + 60 = 210 students did not read Business India. Option (d) is correct
- Explanation :
The following Venn diagram would give us the overall structure of the numbers involved in this situation:
 The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
The number of students who read only Business India in May 2007 = 350 - 120 = 230. Option
(c) is correct
The solutions to the question can be read off from the given diagrams.
The total number of students surveyed = 40 + 50 + 60 + 20 + 30 + 40 + 110 = 350.
The number of students who read only Business India in May 2007 = 350 - 120 = 230. Option
(c) is correct
Ans .
(b) 350
Ans .
(d) None of these
Ans .
(c) 230
Ans .
(b) The carcinogenic effect of RTC could be neutralized by the other ingredients found in coffee.
- Explanation :
If the other ingredients in coffee have a neutralising effect on the carcinogenic effects of RTC, then the conclusion "Use of coffee can cause cancer" is most seriously weakened. Option (b) is the correct answer.
Ans .
(a) 9, 2, 2
- Explanation :
In order to visualise the different ways in which 36 can be written as a product of 3 factors, we first need to think of the factors of 36 above and including the square root of 36. These are: 36 itself, 18, 12, 9, 6 The different ways in which a product of 36 can be formed using 3 numbers are 36 ¥ 1 ¥ 1 (sum of the factors = 36 + 1 + 1 = 38); 18 ¥ 2 ¥ 1 (sum of the factors =18 + 2 + 1 = 21); 12 ¥ 3 ¥ 1 (sum of the factors = 12 + 3 + 1 = 16); 9 ¥ 4 ¥ 1 (sum of the factors = 9 + 4 + 1 = 14); 9 ¥ 2 ¥ 2 (sum of the factors = 9 + 2 + 2 = 13); 6 ¥ 3 ¥ 2 (sum of the factors = 6 + 3 + 2 = 11); 6 ¥ 6 ¥ 1 (sum of the factors = 6 + 6 +1 = 13). Now the key to this question is to think of why the census taker cannot answer the question even though he knows that the sum of the ages is equal to the house number next door (which he has seen when he takes a walk to the next door). In order to understand this, suppose the census taker had seen that the house next door was numbered 38. In such a case, he would have no issues identifying 36, 1 and 1 as the three ages. Similarly, if the house next door was numbered 21,16,14 or 11 the census taker would immediately be able to deduce the three ages. Since, he asks for more information it means that he must be having two solutions for the ages-where the sum of ages were equal. This happens in the case of 9 + 2 + 2 = 13 = 6 + 6 + 1. The moment he knows that she has an eldest child, he rules out the possibility of the ages being 6, 6 and 1. Thus, the ages of the three children are 9, 2 and 2. Option (a) is correct