NUMBERS
- Explanation :
8888 + 888 + 88 + 8 = 9872
- Explanation :
Let x - 1936248 = 1635773. Then, x = 1635773 + 1936248 = 3572021
- Explanation :
We may analyse the given equation as shown : Clearly, 2 + P + R + Q = ll. So, the maximum value of Q can be (11 - 2) i.e., 9 (when P = 0, R = 0);
1 2 + 5 P 9 + 3 R 7 + 2 Q 8 --------- = 1 11 4
- Explanation :
5793405 x 9999 = 5793405(10000-1) = 57934050000-5793405 = 57928256595.b
- Explanation :
986 x 137 + 986 x 863 = 986 x (137 + 863) = 986 x 1000 = 986000.
- Explanation :
1605 x 1605 = \((1605)^2\)= \((1600 + 5)^2 \)= \((1600)^2 + (5)^2\) + 2 x 1600 x 5 = 2560000 + 25 + 16000 = 2576025
- Explanation :
\((a^2 + b^2)\) = \(\sqrt{(a+b)^2+(a-b)^2}\)....formula
\((313)^2 + (287)^2\)= \(\sqrt{(313 + 287)^2 + (313 - 287)^2}\) = \(\sqrt{(600)2 + (26)2}\) = \(\sqrt{(360000 + 676)}\) = 180338.
- Explanation :
Clearly, 16 > Ö241. Prime numbers less than 16 are 2, 3, 5, 7, 11, 13. 241 is not divisible by any one of them. 241 is a prime number
- Explanation :
Clearly, unit's digit in the given product = unit's digit in \(7^{163} * 1^{72}.\)
Now, 74 gives unit digit 1. \(7^{162}\) gives unit digit 1, =\(7^{163}\) gives unit digit (l x 7) = 7. Also, \(1^{72}\)gives unit digit 1. Hence, unit's digit in the product = (7 x 1) = 7.
- Explanation :
Required unit's digit = unit's digit in \((4)^{102} + (4)^{103}\). Now,\( 4^2\) gives unit digit 6 =\((4)^{102}\) gives unjt digit 6 =\((4)^103\) gives unit digit of the product (6 x 4) i.e., 4. Hence, unit's digit in \((264)^m + (264)^{103}\) = unit's digit in (6 + 4) = 0.
- Explanation :
\((4)^{11} * (7)^5 * (11)^2\)= \((2*2)^{11} *(7)^5 *(11)^2\) = \(2^{11} * 2^{11} * 7^5 * 11^2\) = \(2^{22} * 7^5 * 11^2\) Total number of prime factors = (22 + 5 + 2) = 29.
- Explanation :
Given exp = \((896)^2 - (204)^2\) = (896 + 204) (896 - 204) = 1100 * 692 = 761200.
- Explanation :
Sum of digits in 541326 = (5 + 4 + 1 + 3 + 2 + 6) = 21, which is divisible by 3. Hence, 541326 is divisible by 3.
- Explanation :
Let the missing digit be x. Sum of digits = (1 + 9 + 7 + x + 5 + 4 + 6 +2) = (34 + x). For (34 + x) to be divisible by 9, x must be replaced by 2 . Hence, the digit in place of * must be 2.
- Explanation :
The number formed by the last two digits in the given number is 72, which is divisible by 4. Hence, 618703572 is divisible by 4.
- Explanation :
Since the given number is divisible by 5, so 0 or 5 must come in place of $. But, a number ending with 5 is never divisible by 8. So, 0 will replace $. Now, the number formed by the last three digits is 4*0, which becomes divisible by 8, if * is replaced by 4. Hence, digits in place of * and $ are 4 and 0 respectively.
- Explanation :
(Sum of digits at odd places) - (Sum of digits at even places) = (8 + 7 + 3 + 4) - (1 + 2 + 8) = 11, which is divisible by 11. Hence, 4832718 is divisible by 11.
- Explanation :
24 = 3 x 8, where 3 and 8 are co-primes. The sum of the digits in the 52563744 number is 36, which is divisible by 3. So, the given number is divisible by 3. The number formed by the last 3 digits of the given number is 744, which is divisible by 8. So, the given number is divisible by 8. Thus, the given number is divisible by both 3 and 8, where 3 and 8 are co-primes. So, it is divisible by 3 x 8, i.e., 24.
- Explanation :
On dividing 3000 by 19, we get 17 as remainder. Number to be added = (19 - 17) = 2.
- Explanation :
On dividing 2000 by 17, we get 11 as remainder. =Required number to be subtracted = 11.
- Explanation :
On dividing 3105 by 21, we get 18 as remainder. Number to be added to 3105 = (21 - 18) = 3. Hence, required number = 3105 + 3 = 3108.
- Explanation :
Smallest number of 6 digits is 100000. On dividing 100000 by 111, we get 100 as remainder. Number to be added = (111 - 100) - 11. Hence, required number = 100011.
- Explanation :
Divisor = (Dividend - Remainder)/ Quotient= (15968-37)/89 =179
- Explanation :
On dividing the given number by 342, let k be the quotient and 47 as remainder. Then, number – 342k + 47 = (19 x 18k + 19 x 2 + 9) = 19 (18k + 2) + 9. The given number when divided by 19, gives (18k + 2) as quotient and 9 as remainder.
- Explanation :
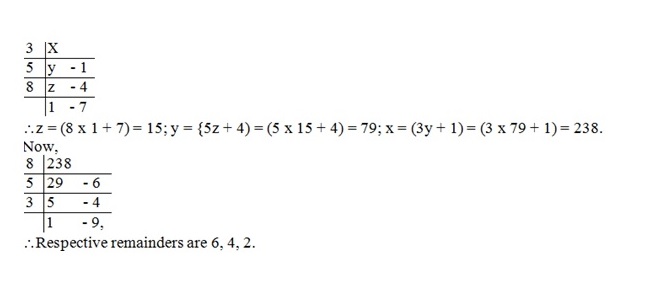
- Explanation :
\(2^{10}\) = 1024. Unit digit of \(2^{10}\) x \(2^{10}\) x \(2^{10}\) is 4 [as 4 x 4 x 4 gives unit digit 4].Unit digit of 231 is 8.Now, 8 when divided by 5, gives 3 as remainder. Hence, 231 when divided by 5, gives 3 as remainder.
- Explanation :
The required numbers are 14, 21, 28, 35, 77, 84. This is an A.P. with a = 14 and d = (21 - 14) = 7. Let it contain n terms.Then, Tn = 84 => a + (n - 1) d = 84 => 14 + (n - 1) x 7 = 84 or n = 11. Required number of terms = 11.
- Explanation :
The given numbers are 1, 3, 5, 7, , 99. This is an A.P. with a = 1 and d = 2. Let it contain n terms. Then, 1 + (n - 1) * 2 = 99 or n = 50. Required sum = \(\frac{n *(first term + last term)}{2}\) = \(\frac {50 *(1 + 99)}{2}\) = 2500.
- Explanation :
All 2 digit numbers divisible by 3 are : 12, 51, 18, 21, , 99. This is an A.P. with a = 12 and d = 3. Let it contain n terms. Then, 12 + (n - 1) x 3 = 99 or n = 30. Required sum = \(\frac {30 * (12+99)}{2}\) = 1665.
- Explanation :
Clearly 2,4,8,16……..1024 form a GP. With a=2 and r = 4/2 =2. Let the number of terms be n . Then 2 x \(2^{n-1}\) =1024 or \(2^{n-1}\) =512 = \(2^9\).
- Explanation :
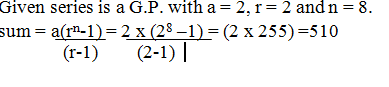
- Explanation :
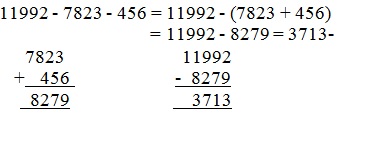
- Explanation :
Let 8597 - x = 7429 - 4358. Then, x = (8597 + 4358) - 7429 = 12955 - 7429 = 5526.
- Explanation :
839478 x 625 = 839478 x \(5^4\) = \(\frac {8394780000}{16}\)= 524673750.
- Explanation :
983 x 207 - 983 x 107 = 983 x (207 - 107) = 983 x 100 = 98300.
- Explanation :
1398 x 1398 - (1398)2 = (1400 - 2)2= (1400)2 + (2)2 - 2 x 1400 x 2 =1960000 + 4 - 5600 = 1954404.
- Explanation :
Given exp = \((387)^2\)+ \((114)^2\)+ (2 x 387x 114) = \(a^2\) + \(b^2\) + 2ab, where a = 387,b=114 = \((a+b)^2\) = \((387 + 114 )^2\) = \((501)^2\) = 251001.
- Explanation :
Given exp = \((81)^2\) + \((68)^2\) – 2x 81 x 68 = \(a^2\) + \(b^2\) – 2ab,Where a =81,b=68 = \((a-b)^2\)= \((81 –68)^2\) = \((13)^2\) = 169.