SQUARE AND CUBE ROOTS
- Explanation :
Express the given number as the product of prime factors.
Now, take the product of these prime factors choosing one out of every pair of the same primes.
This product gives the square root of the given number.
Thus, resolving 6084 into prime factors, we get:
 6084 = \(2^2\) x \(3^2\) x \(13^2\)
6084 = \(2^2\) x \(3^2\) x \(13^2\)
\(\sqrt {6084}\) = (2 x 3 x 13) = 78
- Explanation :
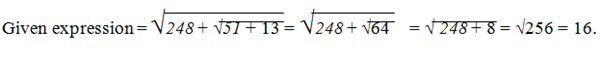
- Explanation :
6 * 15 * 3 = \(\sqrt{(6 + 2)(15 + 3)}\) / (3 + 1) = \(\sqrt {8 * 18}\) / 4 = \(\sqrt {144}\) / 4 = 12 / 4 = 3.
- Explanation :
\(\sqrt {25/16}\)=5/4
- Explanation :
\(\sqrt{0.0009}\)= \(\sqrt {9 / 1000}\) = 3 / 100 = 0.03.
- Explanation :
We make even number of decimal places by affixing a zero, if necessary.
Now, we mark off periods and extract the square root as shown.
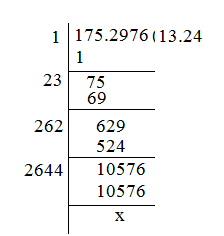 \(\sqrt {175.2976}\) = 13.24
\(\sqrt {175.2976}\) = 13.24
- Explanation :
Let \(\sqrt {86.49}\) + \(\sqrt {5 + x*x}\) = 12.3.
Then, 9.3 + \(\sqrt {5+x*x}\) = 12.3
\(\sqrt {5+x*x}\) = 12.3 - 9.3 = 3x
5 +\( x^2\) = 9
\(x^2\) = 9 - 5= 4
x = √4 = 2.
- Explanation :
√0.289 / 0.00121 = √0.28900/0.00121 = √28900/121 = 170 / 11.
- Explanation :
\(\sqrt {1 + (x / 144)}\) = 13 / 12
( 1 + (x / 144)) = (\(13 / 12 )^2\) = 169 / 144
x / 144 = (169 / 144) - 1
x / 144 = 25/144
x = 25.
- Explanation :
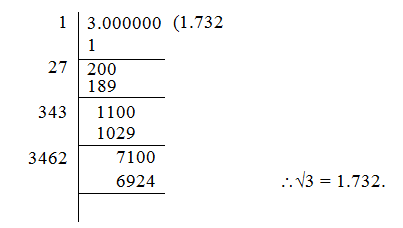
- Explanation :
\(\sqrt {192}\) - \(\frac {1 }{ 2}\)\(\sqrt {48}\) - \(\sqrt {75}\) = \(\sqrt {64 * 3}\) - \(\frac {1}{2}\)\(\sqrt {16 * 3}\) - \(\sqrt {25 * 3}\)
=8\(\sqrt{3}\) - (1/2) * 4\(\sqrt {3}\) - 5\(\sqrt {3}\)
=3\(\sqrt {3}\) - 2\(\sqrt {3}\) = \(\sqrt{3 = 1.732
- Explanation :
Now, since the sum of decimal places in the numerator and denominator under the radical sign is the same, we remove the decimal.br/> Given exp = \(\sqrt{(95 * 85 * 18900) / (17 * 19 * 21)}\) = \(\sqrt (5 * 5 * 900)\) = 5 * 30 = 150.
- Explanation :
Given exp. = √{[\(( 12.1 )^2\) - \((8.1)^2\)] / [\((0.25)^2\)}\) + (0.25)(19.95)]
=√ (20.2 * 4) /( 0.25 * 20.2) = √ 4 / 0.25 = √400 / 25 = √16 = 4.
- Explanation :
\(x^2\) + \(y^2\) = \((1 + √2)^2\) + \((1 - √2)^2\) = 2[\((1)^2\) + \((√2)^2\)] = 2 * 3 = 6.
- Explanation :
- Explanation :
\(\sqrt {(5/3)}\) = \(\sqrt{(5 * 3) / (3 * 3)}\) = \(\sqrt {15 / 3 }\)= 3.88 / 3 = 1.2933…. = 1.293.
- Explanation :
L.C.M. of 10, 12, 15, 18 = 180. Now, 180 = 2 * 2 * 3 * 3 *5 = 22 * 32 * 5.
To make it a perfect square, it must be multiplied by 5.
Required number = (22 * 32 * 52) = 900.
- Explanation :

- Explanation :
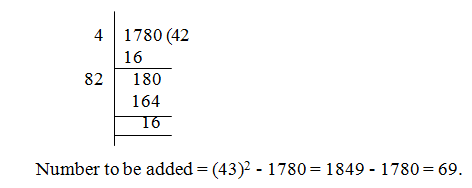
- Explanation :
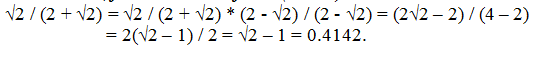
- Explanation :
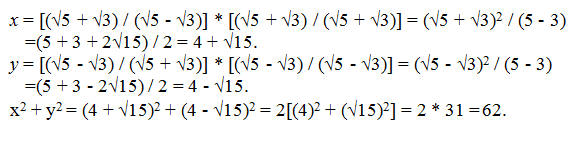
- Explanation :
Resolve the given number as the product of prime factors and take the product of prime factors, choosing one out of three of the same prime factors. Resolving 2744 as the product of prime factors, we get:
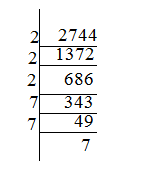
2744 = \(2^3\) x \(7^3\).
3√2744= 2 x 7 = 14.
- Explanation :
Clearly, 4320 = \(2^3\) * \(3^3\) * \(2^2\) * 5. To make it a perfect cube, it must be multiplied by 2 * \(5^2\) i.e,50.