SURDS AND INDICES
- Explanation :
\(1024^{-4/5}\) = \((4^5)^{-4/5}\) =\( 4 ^{ 5 * ( (-4) / 5 )}\) = \(4^{-4}\)= 1 / \(4^4\) = 1 / 256
- Explanation :
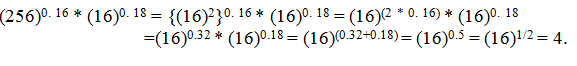
- Explanation :
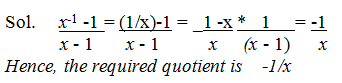
- Explanation :
\(2^{x - 1}\) + \(2^{x+ 1}\) = 1280
2x-1 (1 +\(2^2\))= 1280
\(2^{x-1}\) = 1280 / 5 = 256 = \(2^8\)
x -1 = 8
x = 9.
- Explanation :
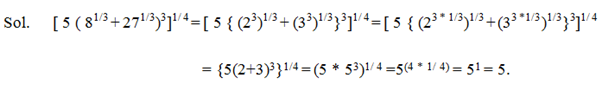
- Explanation :
\((16)^{3/2}\) + \((16)^{-3/2}\)= \((4^2)^{3/2}\) +\((4^2)^{-3/2}\)= \(4^{2 * 3/2}\) +\( 4^{ 2* (-3/2)}\)=
= \(4^3\) +\( 4^{-3}\) = \(4^3\) + (1/\(4^3\) = ( 64 + ( 1/64)) = 4097/64.
- Explanation :
\((1/5)^3y\) = 0.008 = 8/1000 = 1/125 = \((1/5)^3\)
3y = 3
Y = 1.
\((0.25)^y\) = \((0.25)^1\) = 0.25.
- Explanation :
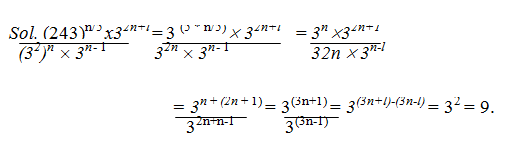
- Explanation :
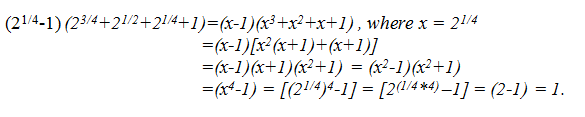
- Explanation :
\(z^1\)= \(x^c\) =\((y^a)^c\) [since x= ya]
=\(y^{(ac)}\) = \((zb)^{ac}\) [since y=zb]
=\(zb^{(ac)}\)= \(z^{abc}\)
abc = 1.
- Explanation :
Given surds are of order 2 and 3. Their L.C.M. is 6. Changing each to a surd of order 6, we get:
\(\sqrt { 2}\) = \( 2^{1/2}\)= \(2^{(1/2)*(3/2)}\)=\(2^{3/6}\)=\(8^{1/6}\)=\(\sqrt [6]{8}\)
\(\sqrt [3]{3}\)= \(3^{1/3}\)=\(3^{(1/3)*(2/2)}\)==\( 3^{2/6}\) = \((3^2)^{1/6}\) = \((9)^{1/6}\) = \(\sqrt[6]{9}\)
Clearly, 6√9 > 6√8 and hence 3√3 > √2.
- Explanation :
Given surds are of order 4, 2 and 3 respectively. Their L.C,M, is 12, Changing each to a surd of order 12, we get: