Q.1

Find the simple interest on Rs.68,000 at 16 2/3% per annum for 9 months

8000

8500

7500

9000

Ans .

8500

Explanation :
P= Rs.6800,R= 50/3%p.a and T =9/12years=3/4 years.

S.I=(P*R*T)/100=Rs(68,000*(50/3)*(3/4)*(1/100))=Rs.8500

Q.2

Find Simple Interest on Rs.3000 at 6 1/4% per annum for the period from

4th Feb,2005 to 18th April,2005.

37.50

45.00

35.50

38.00

Ans .

37.50

Explanation :

S.I. = Rs.(3,000*(25/4)*(1/5)*(1/100))= Rs.37.50.

Q.3

A sum at simple interests at 13 ½ % per annum amounts to Rs.2502.50 after 4 years find the sum.

2625

1615

1630

1625

Ans .

1625

Explanation :
Let sum be Rs. x then , S.I.=Rs.(x$\frac{27}{2}$*4*(1/100) ) = Rs.27x/50
amount = (Rs. x+$\frac{27x}{50}$ = $\frac{77x}{50}$
$\frac{77x}{50}$ = 2502.50
x = $ \frac{2502.50x50}{70}$
= 1625 Hence , sum = Rs.1625.

Q.4

A sum of Rs. 800 amounts to Rs. 920 in 8 years at simple interest

interest rate is increased by 8%, it would amount to bow mucb ?

950

992

192

882

Ans .

992

Explanation :
S.l. = Rs. (920 - 800) = Rs. 120; p = Rs. 800, T = 3 yrs.
R = ((100 x 120)/(800*3) ) % = 5%. New rate = (5 + 3)% = 8%. New S.l. = Rs. (800*8*3)/100 = Rs. 192.
New amount = Rs.(800+192) = Rs. 992.

Q.5

Adam borrowed some money at the rate of 6% p.a. for the first two years , at the rate of 9% p.a. for the next three years and at the rate of 14% p.a.

for the period beyond five years.1£ he pays a total interest of Rs. 11, 400 at the end of nine years how much money did he borrow ?

12,050

11,500

12,000

11,000

Ans .

12,000

Explanation :
Let the sum borrowed be x.
Then,(x*2*6)/100 + (x*9*3)/100 + (x*14*4)/100 = 11400
(3x/25 + 27x/100 + 14x / 25) = 11400
95x/100 = 11400  x = (11400*100)/95 = 12000.
Hence , sum borrowed = Rs.12,000.

Q.6

A certain sum of money amounts to Rs. 1008 in 2 years and to Rs.1164 in 3 ½ years. Find the sum and rate of interests.

208 ,13%

208 ,15%

308 ,13%

308 ,15%

Ans .

208 ,13%

Explanation :
S.I. for 1 ½ years = Rs.(1164-1008) = Rs.156.
S.l. for 2 years = Rs.(156*(2/3)*2)=Rs.208
Principal = Rs. (1008 - 208) = Rs. 800.
Now, P = 800, T = 2 and S.l. = 208.
Rate=(100* 208)/(800*2)% = 13

Q.7

At what rate percent per annum will a sum of money double in 16 years.

7$\frac{1}{5}$% p.a

6$\frac{1}{3}$% p.a

7$\frac{1}{4}$% p.a

6$\frac{1}{4}$% p.a

Ans .

6$\frac{1}{4}$% p.a

Explanation :
Let principal = P. Then, S.l. = P and T = 16 yrs.
Rate = (100 x P)/(P*16)% = 6$\frac{1}{4}$% p.a.

Q.8

The simple interest on a sum of money is 4/9 of the principal .Find the rate percent and time, if both are numerically equal.

6$\frac{1}{4}$% p.a., 6 yrs 5 months

6$\frac{2}{3}$% p.a., 6 yrs 8 months

6$\frac{2}{3}$% p.a., 2 yrs 8 months

6$\frac{1}{4}$% p.a., 6 yrs 9 months

Ans .

6$\frac{2}{3}$% p.a., 6 yrs 8 months

Explanation :
Let sum = Rs. x. Then, S.l. = Rs. 4x/9
Let rate = R% and time = R year.
Then, (x*R*R)/100=4x/9 or $R^2$ =400/9 or R = 20/3 = 6 2/3.
Rate = 6$\frac{2}{3}$ % and Time = 6$\frac{2}{3}$ = 6 years 8 months.

Q.9

The simple interest on a certain sum of money for 2 l/2 years at 12% per annum is Rs. 40

less tban the simple interest on the same sum for 3 ½ years at 10% per annum.Find the sum.

800

1000

900

750

Ans .

800

Explanation :
Let the sum be Rs. x Then,$\frac{x*10*7}{100*2}$ – $\frac{x*12*5}{100*2}$ = 40
$\frac{7x}{20}$-$\frac{3x}{10}$=40
x = (40 * 20) = 800.
Hence, the sum is Rs. 800.

Q.10

A sum was put at simple interest at a certain rate for 3 years. Had it been put at 2% higher rate,

it would have fetched Rs. 360 more.Find the sum.

6500

5000

6000

5900

Ans .

6000

Explanation :
. Let sum = P and original rate = R.
Then, [ (P*(R+2)*3)/100] – [ (P*R*3)/100] = 360.
3PR + 6P - 3PR = 36000
6P=36000
P=6000
Hence, sum = Rs. 6000

Q.11 What annual instalment will discharge a debt of Rs. 1092 due in 3 years at 12% simple interest?

325

225

300

425

Ans .

325

Explanation :
.Let each Instalment be Rs. x
Then, ( x+ $\frac{x*12*1}{100}$ + x\(\frac{x*12*2}{100}\ ) + x = 1092
((28x/25) + (31x/25) + x) = 1092
(28x+31x+25x)=(1092*25)
x= (1092*25)/84 = Rs.325. Each instalment = Rs. 325.

Q.12

A sum of Rs. 1550 is lent out into two parts, one at 8% and another one at 6%.

If the total annual income is Rs. 106, find the money lent at each rate.

700,900

650,650

650,700

650,900

Ans .

650 ,900

Explanation :
Let the sum lent at 8% be Rs. x and that at 6% be Rs. (1550 - x).
$\frac{x*8*1}{100}$ + $\frac{(1550-x)*6*1}{100}$=106
8x + 9300 –6x=10600
2x = 1300 x = 650.
Money lent at 8% = Rs. 650. Money lent at 6% = Rs. (1550 - 650) = Rs. 900.

Q.13

Find compound interest on Rs. 7500 at 4% per annum for 2 years, compounded annually.

612

620

650

510

Ans .

612

Explanation :
Amount = Rs [7500*$(1+(4/100)^2$] = Rs (7500 * (26/25) * (26/25)) = Rs. 8112.
therefore, C.I. = Rs. (8112 - 7500) = Rs. 612.

Q.14

Find compound interest on Rs. 8000 at 15% per annum for 2 years 4 months, compounded annually.

2000

2109

3109

3000

Ans .

3109

Explanation :
Time = 2 years 4 months = 2(4/12) years = 2(1/3) years.
Amount = Rs'. [8000 X $(1+(15/100))^2$ X (1+((1/3)*15)/100)]
=Rs. [8000 * (23/20) * (23/20) * (21/20)] = Rs. 11109. .
C.I. = Rs. (11109 - 8000) = Rs. 3109.

Q.15

Find the compound interest on Rs. 10,000 in 2 years at 4% per annum, the interest being compounded half-yearly

830

825.32

825

824.32

Ans .

824.32

Explanation :
Principal = Rs. 10000; Rate = 2% per half-year; Time = 2 years = 4 half-years.
Amount = Rs [10000 *$ (1+(2/100))^4$]
= Rs(10000 * (51/50) * (51/50) * (51/50) * (51/50)) = Rs. 10824.32.
C.I. = Rs. (10824.32 - 10000) = Rs. 824.32.

Q.16

Find the compound interest on Rs. 16,000 at 20% per annum for 9 months,compounded quarterly

2000

2522

3522

3500

Ans .

2522

Explanation :
Principal = Rs. 16000; Time = 9 months =3 quarters;Rate = 20% per annum = 5% per quarter.
Amount = Rs. [16000 x $(1+(5/100))^3$] = Rs. 18522.
CJ. = Rs. (18522 - 16000) = Rs. 2522

Q.17

If the simple interest on a sum of money at 5% per annum for 3 years is Rs. 1200,

find the compound interest on the same sum for the same period at the same rate.

1261

1360

1260

1161

Ans .

1261

Explanation :
Clearly, Rate = 5% p.a., Time = 3 years, S.I.= Rs. 1200
So principal=RS [100*1200]/3*5= RS 8000 Amount = Rs. 8000 x $[1 +5/100]^3$= Rs. 9261.
C.I. = Rs. (9261 - 8000) = Rs. 1261.

Q.18 In what time will Rs. 1000 become Rs. 1331 at 10% per annum compounded annually?

2 ys

3 yrs

4 yrs

2 yrs 5 months

Ans .

3 yrs

Explanation :
Principal = Rs. 1000; Amount = Rs. 1331; Rate = 10% p.a. Let the time be n years.
Then, [ 1000 (1+ $(10/100))^n$ ] = 1331 or $(11/10)^n$ = (1331/1000) = $(11/10)^3$
n= 3 years.

Q.19

If Rs. 600 amounts to Rs. 683.20 in two years compounded annually, find the rate of interest per annum.

8% p.a.

10% p.a.

5% p.a.

7% p.a.

Ans .

8% p.a.

Explanation :
Principal = Rs. 500; Amount = Rs. 583.20; Time = 2 years.
Let the rate be R% per annum.. 'Then, [ 500 $(1+(R/100)^2$ ] = 583.20 or $[1+ (R/100)]^2$ = 5832/5000 = 11664/10000
$[ 1+ (R/100)]^2$ = $(108/100)^2$ or 1 + (R/100) = 108/100 or R = 8
So, rate = 8% p.a.

Q.20

. If the compound interest on a certain sum at 16 (2/3)% to 3 years is Rs.1270, find the simple interest

on the same sum at the same rate and f or the same period.

1080

1050

1110

2050

Ans .

1080

Explanation :
Let the sum be Rs. x.
Then, C.I. = [ x * (1 + $( 50/(3*100))^3$ - x ] = ((343x / 216) - x) = 127x / 216
127x /216 = 1270 or x = (1270 * 216) / 127 = 2160.
Thus, the sum is Rs. 2160 S.I. = Rs ( 2160 * (50/3) * 3 * (1 /100 ) ) = Rs. 1080.

Q.21

The difference between the compound interest and simple interest on a certain

sum at 10% per annum for 2 years is Rs. 631. Find the sum.

Rs.53,110.

Rs.63,100.

Rs.60,000.

Rs.73,100.

Ans .

Rs.63,100.

Explanation :
Let the sum be Rs. x. Then,
C.I. = x $( 1 + ( 10 /100 ))^2$- x = 21x / 100 , S.I. = (( x * 10 * 2) / 100) = x / 5
(C.I) - (S.I) = ((21x / 100 ) - (x / 5 )) = x / 100
Hence, the sum is Rs.63,100.

Q.22

The difference between the compound interest and the simple interest accrued on an amount of Rs. 18,000

in 2 years was Rs. 405. What was the rate of interest p.c.p.a. ?

7%.

11%.

13%.

15%.

Ans .

15%.

Explanation :
Let the rate be R% p.a.
then, [ 18000 ( 1 + $( R / 100 )^2$ ) - 18000 ] - ((18000 * R * 2) / 100 )
= 405 18000 [ ( 100 + $(R / 100 )^2 $ / 10000) - 1 - (2R / 100 ) ]
= 405 18000[( $(100 + R ) ^2$ - 10000 - 200R) / 10000 ]
= 405 9$R^2$ / 5 = 405 $R^2$ =((405 * 5 ) / 9) = 225
R = 15. Rate = 15%.

Q.23

Divide Rs. 1301 between A and B, so that the amount of A after 7 years is equal to the amount of B after 9 years,

the interest being compounded at 4% per annum.

Rs.676 and rs.665.

Rs.676 and Rs.625.

Rs.776 and Rs.725.

Rs.576 and Rs.625.

Ans .

Rs.676 and Rs.625.

Explanation :
Let the two parts be Rs. x and Rs. (1301 - x).
x$(1+4/100)^7$ =$(1301-x)(1+4/100)^9$ x/(1301-x)=$(1+4/100)^2$=(26/25*26/25) 625x=676(1301-x) 1301x
=676*1301 x=676. So,the parts are rs.676 and rs.(1301-676)i.e rs.676 and rs.625.

Q.24

a certain sum amounts to rs.7350 in 2 years and to rs.8575 in 3 years.find the sum and rate percent.

Rs.5200

Rs.5000

Rs.4400

Rs.5400

Ans .

Rs.5400

Explanation :
S.I on rs.7350 for 1 year=rs.(8575-7350)=rs.1225.
Rate=(100*1225/7350*1)%=16 2/3%
Let the sum be rs.x.then, X$(1+50/3*100)^2$=7350 X*7/6*7/6=7350
X=(7350*36/49)=5400. Sum=rs.5400

Q.25

.a sum of money amounts to rs.6690 after 3 years and to rs.10,035 after

6 years on compound interest.find the sum.

Rs.4460.

Rs.4660.

Rs.5560.

Rs.3460.

Ans .

Rs.4460.

Explanation :
. Let the sum be rs.P.then P$(1+R/100)^3$=6690…(i) and P$(1+R/100)^6$=10035…(ii)
On dividing,we get $(1+R/100)^3$=10025/6690=3/2.
Substituting this value in (i),we get: P*3/2=6690 or P=(6690*2/3)=4460
Hence,the sum is rs.4460.

Q.26

a sum of money doubles itself at compound interest in 15 years.in how many years will it beco,e eight times?

55 years

25 years

35 years

45 years

Ans .

45 years

Explanation :
$P(1+R/100)^15$=2P $(1+R/100)^15$=2P/P=2
LET $P(1+R/100)^n$=8P
$(1+R/100)^n$=8=23=$((1+R/100)^15))^3$
[USING (I)]
$(1+R/100)^N$=$(1+R/100)^45$ n=45.
Thus,the required time=45 years

Q.27

What annual payment will discharge a debt of Rs.7620 due in 3years at 16 2/3% per annum interest?

Rs.4430

Rs.3550

Rs.3430

Rs.5430

Ans .

Rs.3430

Explanation :
Let each installment beRs.x.
Then,(P.W. of Rs.x due 1 year hence)+(P>W of Rs.x due 2 years hence)+(P.W of Rs. X due 3years hence)=7620.
x/(1+(50/3*100))+ x/$(1+(50/3*100))^2$ + x/$(1+(50/3*100))^3$=7620
(6x/7)+(936x/49)+(216x/343)=7620.

294x+252x+216x=7620*343.
x=(7620*343/762)=3430.
Amount of each installment=Rs.3430.

Q.28

1.Evaluate:(1)$log_3$(27) (2)$log_7$(1/343)(3)$log_100$(0.01)

-3,-3,1s

-3,-3,-1

3,3,1

3,-3,-1

Ans .

3,-3,-1

Explanation :
(1) let LOG(3, 27)=$3^3$ or n=3.
ie, $log_3$(27)= 3.
(2) Let $log_7$(1\343) = n.
Then ,7n =1/343=1/73
n = -3.ie,log7(1\343)= -3.
(3) let $log_100$(0.01) = n.
Then,. (100) = 0.01 = 1 /100=100 -1 0r n=-1

Q.29

(i) $\log_{7} 1$(ii)$\log_{34} 34$ (iii)$36^{\log_{6} 4} $

0,0,16

0,0,0

4,2,16

3,0,4

Ans .

0,0,16

Reference https://www.physicsforums.com/threads/how-to-write-log-in-latex.817954/

Explanation :
solution: i) we know that $log_a$ 1=0 ,so $log_7$ 1=0 . ii) we know that $log_a$a=1,so $\log_{34} 34$ =0. iii) We know that $a^{\log_{6} x}$ =x.
now $36^{\log_{6} 4}$=$6^{2^{\log_{6} 4}} $ =$6^{\log_{6} 16}$=16.

Q.30

if $\log_{\sqrt{8}} x$=3 (1/3), find the value of x.

Ans .

Explanation :
$\log_{\sqrt{8}} x$=10/3
x=$\sqrt{8}^{10/3}$ =$2^{\frac{2}{3} ^{\frac{10}{3}}}$=$2^{\frac{2}{3} * \frac{10}{3}}$=25=32.

Q.31

(i) $\log_{5} 3$* $\log_{27} 25$(ii) $\log_{10} 27$ – $\log_{27} 9$

3/2,6/5

2/3,5/6

3/2,5/6

2/3,6/5

Ans .

2/3,5/6

Explanation :
$\log_{5} 3$* $\log_{27} 25 $=log 3/log 5*log 25/log 27 =(log 3 /log 5) * log$5^2$ *log$3^3$
=(log 3/log 5)*(2log 5 / 3(log 3)
=2/3
(ii)Let $\log_{9} 27$=n
Then,$9^n$ =27 $3^{2n}$ =$3^3$ 2n=3 n=3/2
Again, let $\log_{27} 9$=m
Then,$27^m$ =9 $3^{3m}$ =$3 ^2$ 3m=2 m=2/3
$\log_{9} 27$- $\log_{27} 9$=(n-m)=(3/2-2/3)=5/6

Q.32

Simplify :(log 75/16-2 log 5/9+log 32/243)

log 2

log 4

Ans .

log2

Explanation :
log 75/16-2 log 5/9+log 32/243
= log 75/16-log(5/9)2+log32/243
= log 75/16-log25/81+log 32/243
= log(75/16*32/243*81/25)=log 2

Q.33

6.Find the value of x which satisfies the relation

$\log_{10} 3$+$\log_{10} (4x+1)$=$\log_{10} (x+1)$+1

3/5

7/2

5/6

Ans .

7/2

Explanation :
$\log_{10} 3$+$\log_{10} (4x+1)$=$\log_{10} (x+1)$+1
$\log_{10} 3$+$\log_{10} (4x+1)$=$\log_{10} (x+1)$+$\log_{10} (x+1)$+$\log_{10} 10$
$\log_{10} (3(4x+1))$=$\log_{10} (10(x+1))$ =3(4x+1)=10(x+1)=12x+3 =10x+10 =2x=7=x=7/2

Q.34

.Simplify:[1/$\log_{xy} (xyz)$ +1/$\log_{yz} (xyz)$+1/$\log_{zx} (xyz)$]

Ans .

Explanation :
$\log_{xyz} (xy)$ + $\log_{xyz} (yz)$ + $\log_{xyz} (zx)$
=$\log_{xyz} (xy*yz*zx)$=$\log_{xyz} {(xyz)^2}$ 2$\log_{xyz} (xyz)$ =2*1=2

Q.35

If log 2=0.30103,find the value of log 50.

0.69897

1.69897

2.69897

Ans .

1.69897

Explanation :
log 50=log (100/2)=log 100-log 2=2-0.30103=1.69897.

Q.36

If log 2=0.3010 and log 3=0.4771,find the values of:

i) log 25 ii)log 4.5

1.39,0.65

1.98,0.32

2,1

4,3

Ans .

1.39,0.65

Explanation :
i) log 25=log(100/4)=log 100-log 4=2-2log 2=(2-2*.3010)=1.398.
ii) log 4.5=log(9/2)=log 9-log 2=2log 3-log 2=(2*0.4771-.3010)=0.6532

Q.37

If log 2=.30103,find the number of digits in $2^{56}$.

Ans .

Explanation :
log $2^{56}$ =56 log2=(56*0.30103)=16.85768. Its characteristics is 16. Hence,the number of digits in $2^{56}$ is 17

Q.38

One side of a rectangular field is 15 m and one of its diagonals is 17 m. Find the area of the field.

130 $m^2$

110 $m^2$

120 $m^2$

100 $m^2$

Ans .

120 $m^2$

Explanation :
Other side = ${17}^ 2$- $15^2{^{(1/2)}}$ = $(289- 225)^{1/2}$ = ${64}^{1/2}$ = 8 m.
Area = (15 x 8) $m^2$ = 120 $m^2$

Q.39

A lawn is in the form of a rectangle having its sides in the ratio 2: 3. The

area of the lawn is (1/6) hectares. Find the length and breadth of the lawn.

23/33,60

11/3,55

6/5,65

33/3,50

Ans .

33/3,50

So, 2x * 3x = 5000/3 <=> $x^2$ = 2500/9 <=> x = 50/3

therefore Length = 2x = (100/3) m = 33(1/3) m and Breadth = 3x = 3(50/3) m = 50m.

Q.40

Find the cost of carpeting a room 13 m long and 9 m broad with a carpet

75 cm wide at the rate of Rs. 12.40 per square metre.

Rs. 1934.40.

Rs. 2934.40.

Rs. 2234.40.

Rs. 1834.40.

Ans .

Rs. 1934.40.

Explanation :
Area of the carpet = Area of the room = (13 * 9)$m^2$ = 117 $m^2$. Length of the carpet = (area/width) = 117 *(4/3) m = 156 m. Therefore Cost of carpeting = Rs. (156 * 12.40) = Rs. 1934.40.

Q.41

If the diagonal of a rectangle is 17 cm long and its perimeter is 46 cm,

find the area of the rectangle.

150 $cm^2$

110 $cm^2$

120 $cm^2$

100 $cm^2$

Ans .

120 $cm^2$

Explanation :
Let length = x and breadth = y. Then,
2 (x + y) = 46 or x + y = 23 and $x^2$ + $y^2$ = $17^2$ = 289.
Now, $(x+y)^2$ = $23^2$ <=> ( $x^2$ + $y^2$ ) + 2xy = 529 <=> 289 + 2xy = 529 xy=120
Area = xy = 120 $cm^2$ .

Q.42

The length of a rectangle is twice its breadth. If its length is decreased by 5 cm and

breadth is increased by 5 cm, the area of the rectangle is increased by 75 sq. cm. Find the

length of the rectangle.

30 cm

10 cm

20 cm

15 cm

Ans .

20 cm

Explanation :
Let breadth = x. Then, length = 2x. Then,
(2x - 5) (x + 5) - 2x * x = 75 <=> 5x - 25 = 75 <=> x = 20.
Length of the rectangle = 20 cm.

Q.43

In measuring the sides of a rectangle, one side is taken 5% in excess, and the other 4%

in deficit. Find the error percent in the area calculated from these measurements.

0.5%.

0.8%.

1.8%.

1.6%.

Ans .

0.8%.

Explanation :
Let x and y be the sides of the rectangle. Then, Correct area = xy.
Calculated area = (105/100)*x * (96/100)*y = (504/500 )(xy)
Error In measurement = (504/500)xy- xy = (4/500)xy
Error % = [(4/500)xy *(1/xy) *100] % = (4/5) % = 0.8%.

Q.44

A rectangular grassy plot 110 m. by 65 m has a gravel path 2.5 m wide all round it on

the inside. Find the cost of gravelling the path at 80 paise per sq. metre.

Rs. 715

Rs. 450

Rs. 680

Rs. 550

Ans .

Rs. 680

Explanation :
Area of the plot = (110 x 65) $m^2$ = 7150 $m^2$
Area of the plot excluding the path = [(110 - 5) * (65 - 5)] $m^2$ = 6300 $m^2$ .
Area of the path = (7150 - 6300) $m^2$ = 850 v.
Cost of gravelling the path = Rs.850 * (80/100)= Rs. 680

Q.45

The perimeters of two squares are 40 cm and 32 cm. Find the perimeter of a third

square whose area is equal to the difference of the areas of the two squares.

24 cm

14 cm

34 cm

28 cm

Ans .

24 cm

Explanation :
Side of first square = (40/4) = 10 cm;
Side of second square = (32/4)cm = 8 cm.
Area of third square = [(10) 2 - (8) 2] $cm^2$ = (100 - 64) $cm^2$ = 36 $cm^2$
Side of third square = (36)(1/2) cm = 6 cm.
Required perimeter = (6 x 4) cm = 24 cm.

Q.46

A room 5m 55cm long and 3m 74 cm broad is to be paved with square tiles. Find the

least number of square tiles required to cover the floor.

150

166

160

176

Ans .

176

Explanation :
Area of the room = (544 x 374) $cm^2$.
Size of largest square tile = H.C.F. of 544 cm and 374 cm = 34 cm.
Area of 1 tile = (34 x 34) $cm^2$.
Number of tiles required =(544*374)/(34*34)=176

Q.47

Find the area of a square, one of whose diagonals is 3.8 m long

8.52 $m^2$

7.22 $m^2$

6.43$m^2$

4.2 $m^2$

Ans .

7.22 $m^2$

Explanation :
Area of the square = (1/2)* $(diagonal)^2$ = [(1/2)*3.8*3.8 ]$m^2$ = 7.22 $m^2$ .

Q.48

The diagonals of two squares are in the ratio of 2 : 5. Find the ratio of their areas

7 : 25.

4 : 35.

3: 25.

4 : 25.

Ans .

4 : 25.

Explanation :
Let the diagonals of the squares be 2x and 5x respectively.
Ratio of their areas = (1/2)*$(2x) ^2$ :(1/2)*$(5x)^ 2$ = 4$x^2$ : 25$x^2$ = 4 : 25.

Q.49

If each side of a square is increased by 25%, find the percentage change in its area

55.15%

58.30%

56.25%

60.25%

Ans .

56.25%

Explanation :
Let each side of the square be a. Then, area = $a^2$.
New side =(125a/100) =(5a/4). New area = $(5a/4) ^2$ =(25$a^2$)/16.
Increase in area = ((25 $a^2$)/16)-$a^2$ =(9$a^2$)/16.
Increase% = [((9$a^2$)/16)*(1/$a^2$)*100] % = 56.25%.

Q.50

If the length of a certain rectangle is decreased by 4 cm and the width is increased by

3 cm, a square with the same area as the original rectangle would result. Find the perimeter

of the original rectang

60 cm

40 cm

50 cm

70 cm

Ans .

50 cm

Explanation :
Let x and y be the length and breadth of the rectangle respectively.
Then, x - 4 = y + 3 or x - y = 7 ----(i)
Area of the rectangle =xy; Area of the square = (x - 4) (y + 3)
(x - 4) (y + 3) =xy <=> 3x - 4y = 12 ----(ii)
Solving (i) and (ii), we get x = 16 and y = 9.
Perimeter of the rectangle = 2 (x + y) = [2 (16 + 9)] cm = 50 cm.

Q.51

A room is half as long again as it is broad. The cost of carpeting the at Rs. 5 per sq. m

is Rs. 270 and the cost of papering the four walls at Rs. 10 per m2 is Rs. 1720. If a door and 2

windows occupy 8 sq. m, find the dimensions of the room.

l=9,b=8,h=7

l=9,b=6,h=7

l=6,b=6,h=6

l=9,b=6,h=6

Ans .

l=9,b=6,h=6

Explanation :
Let breadth = x metres, length = 3x metres, height = H metres.
Area of the floor=(Total cost of carpeting)/(Rate/m2)=(270/5)m2=54m2.
x* (3x/2) = 54 <=> $x^2$= (54*2/3) = 36 <=> x = 6.
So, breadth = 6 m and length =(3/2)*6 = 9 m.
Now, papered area = (1720/10)$m^2$ = 172 $m^2$.
Area of 1 door and 2 windows = 8 $m^2$.
Total area of 4 walls = (172 + 8)$m^2$ = 180 $m^2$
2*(9+ 6)* H = 180 <=> H = 180/30 = 6 m.

Q.52

Find the area of a triangle whose sides measure 13 cm, 14 cm and 15 cm

94 $cm^2$.

84 $cm^2$..

74 $cm^2$.

64 $cm^2$.

Ans .

84 $cm^2$..

Explanation :
Let a = 13, b = 14 and c = 15. Then, S = (1/2)(a + b + c) = 21.
(s- a) = 8, (s - b) = 7 and (s - c) = 6.
Area = $(s(s- a) (s - b)(s - c))^{1/2}$ = $(21 *8 * 7*6)^{1/2}$ = 84 $cm^2$.

Q.53

Find the area of a right-angled triangle whose base is 12 cm and hypotenuse is 13cm.

30$cm^2$

20$cm^2$

40$cm^2$

50$cm^2$

Ans .

30$cm^2$

Explanation :
Height of the triangle = [$13^2$ - $12^{2 ^{1/2}}$] cm = $25^{1/2}$ cm = 5 cm.
Its area = (1/2)* Base * Height = ((1/2)*12 * 5) $cm^2$ = 30$cm^2$ .

Q.54

The base of a triangular field is three times its altitude. If the cost of cultivating the

field at Rs. 24.68 per hectare be Rs. 333.18, find its base and height.

Base = 700 m and Altitude = 200 m

Base = 800 m and Altitude = 300 m

Base = 900 m and Altitude = 300 m

Base = 600 m and Altitude = 200 m

Ans .

Base = 900 m and Altitude = 300 m

Explanation :
Area of the field = Total cost/rate = (333.18/25.6)hectares = 13.5 hectares
(13.5 x 10000) $m^2$ = 135000 $m^2$
Let altitude = x metres and base = 3x metres.
Then, (1/2)* 3x * x = 135000 <=>$x^2$ = 90000 <=>x = 300.
Base = 900 m and Altitude = 300 m.

Q.55

The altitude drawn to the base of an isosceles triangle is 8 cm and the perimeter is

32cm. Find the area of the triangle.

60 $cm^2$

70 $cm^2$

50 $cm^2$

80 $cm^2$

Ans .

60 $cm^2$

Explanation :
Let ABC be the isosceles triangle and AD be the altitude.
Let AB = AC = x. Then, BC = (32 - 2x).
Since, in an isosceles triangle, the altitude bisects the base,
so BD = DC = (16 - x).
In triangle ADC, $AC^2$= AD +$DC^2$ =>$x^2$ =(82)+$(16-x) ^2$
=>32x = 320 =>x= 10.
BC = (32- 2x) = (32 - 20) cm = 12 cm.
Hence, required area = ((1/2)x*BC * AD) = ((1/2)*12 *10)$cm^2$ = 60 $cm^2$

Q.56

Find the length of the altitude of an equilateral triangle of side 3$\sqrt{3}$ cm.

6.5 cm.

5.5 cm.

7.5 cm.

4.5 cm.

Ans .

4.5 cm.

Explanation :
Area of the triangle = ($\sqrt{3}$/4) x (3$\sqrt{3}$)2 = 27$\sqrt{3}$. Let the height be h.
Then, (1/2) x 3$\sqrt{3}$ x h = (27$\sqrt{3}$/4) X(2/$\sqrt{3}$) = 4.5 cm.

Q.57

In two triangles, the ratio of the areas is 4 : 3 and the ratio of their heights

is 3 : 4. Find the ratio of their bases.

17 : 9.

16 : 9.

11 : 3

13 : 7

Ans .

16 : 9.

Explanation :
Let the bases of the two triangles be x and y and their heights be 3h and 4h respectively.
Then,
((1/2) X x X 3h)/(1/2) X y X 4h) =4/3 => x/y =(4/3 X 4/3)=16/9
Required ratio = 16 : 9.

Q.58

The base of a parallelogram is twice its height. If the area of the parallelogram

is 72 sq. cm, find its height.

6 cm

9 cm

7 cm

4 cm

Ans .

6 cm

Explanation :
Let the height of the parallelogram be x. cm. Then, base = (2x) cm.
2x X x =72 2$x^2$ = 72 $x^2$ =36 x=6
Hence, height of the parallelogram = 6 cm.

Q.59

Find the area of a rhombus one side of which measures 20 cm and 01 diagonal 24 cm.

384 $cm^2$

344 $cm^2$

388 $cm^2$

376 $cm^2$

Ans .

384 $cm^2$

Explanation :
Let other diagonal = 2x cm.
Since diagonals of a rhombus bisect each other at right angles, we have:
$20^2$ = $12^2$ + $x^2$ x= $\sqrt{20^2-{12^2}}$= 256= 16 cm.
So, other diagonal = 32 cm.
Area of rhombus = (1/2) x (Product of diagonals) = ((1/2)x 24 x 32) $cm^2$ = 384 $cm^2$

Q.60

The difference between two parallel sides of a trapezium is 4 cm. perpendicular

distance between them is 19 cm. If the area of the trapezium is 475 find the lengths of the parallel sides.

28 cm and 25 cm

25 cm and 20 cm

27 cm and 23 cm

30 cm and 28 cm

Ans .

27 cm and 23 cm

Explanation :
Let the two parallel sides of the trapezium be a em and b em.
Then, a - b = 4
And, (1/2) x (a + b) x 19 = 475 --> (a + b) =((475 x 2)/19) --> a + b = 50
Solving (i) and (ii), we get: a = 27, b = 23.
So, the two parallel sides are 27 cm and 23 cm

Q.61

Find the length of a rope by which a cow must be tethered in order tbat it

may be able to graze an area of 9856 sq. metres.

52.

58.

56.

Ans .

paste right option

Explanation :
Clearly, the cow will graze a circular field of area 9856 sq. metres and radius equal to the length of the rope. Let the length of the rope be R metres. Then, $\prod R^2 $= (9856 X (7/22)) = 3136 --> R = 56. Length of the rope = 56 m.

Q.62

The area of a circular field is 13.86 hectares. Find the cost of fencing it at

the rate of Rs. 4.40 per metre.

Rs. 5808

Rs. 5765

Rs. 5450

Rs. 5907

Ans .

Rs. 5808

Explanation :
Area = (13.86 x 10000) $m^2$ = 138600 $m^2$ .
($R^2$ = 138600 ($R^2$ = (138600 x (7/22)) R = 210 m.
Circumference = 2$\prod$R = (2 x (22/7) x 210) m = 1320 m.
Cost of fencing = Rs. (1320 x 4.40) = Rs. 5808.

Q.63

The diameter of the driving wheel of a bus is 140 em. How many revolution, per

minute must the wheel make in order to keep a speed of 66 kmph ?

150.

450.

350.

250.

Ans .

250.

Explanation :
Distance to be covered in 1 min. = $\frac{66 * 1000}{60}$ m = 1100 m.
Circumference of the wheel = (2 x (22/7) x 0.70) m = 4.4 m.
Number of revolutions per min. =(1100/4.4) = 250.

Q.64

A wheel makes 1000 revolutions in covering a distance of 88 km. Find the radius of the wheel.

13 m.

15 m.

14 m.

11 m.

Ans .

14 m.

Explanation :
Distance covered in one revolution =$\frac{88 X 1000}{1000}$= 88m.
2$\prod$R = 88 --> 2 x (22/7) x R = 88 --> R = 88 x (7/44) = 14 m.

Q.65

The inner circumference of a circular race track, 14 m wide, is 440 m. Find

radius of the outer circle.

84 m

74 m

76 m

64 m

Ans .

84 m

Explanation :
Let inner radius be r metres. Then, 2$\prod$r = 440 --> r = (440 x (7/44))= 70 m.
Radius of outer circle = (70 + 14) m = 84 m.

Q.66

Two concentric circles form a ring. The inner and outer circumferences of ring are

(352/7) m and (518/7) m respectively. Find the width of the ring.

7 m

8 m

4 m

5 m

Ans .

4 m

Explanation :
Let the inner and outer radii be r and R metres.
Then 2$\prod$r = (352/7) -->r =((352/7) X (7/22) X (1/2))=8m.
2$\prod$R=(528/7) --> R=((528/7) X (7/22) X (1/2))= 12m.
Width of the ring = (R - r) = (12 - 8) m = 4 m.

Q.67

A sector of 120', cut out from a circle, has an area of (66/7) sq. cm. Find the

radius of the circle.

5 cm.

3 cm.

2 cm.

4 cm.

Ans .

3 cm.

Explanation :
Let the radius of the circle be r cm. Then,
$\frac{\prod r^{2}\theta }{360}$=(66/7) --> (22/7) X $r^2$ X(120/360)= (66/7)
$r^2$=((66/7) X (7/22) X 3) --> r=3. Hence, radius = 3 cm.

Q.68

Find the ratio of the areas of the incircle and circumcircle of a square.

3 : 5.

1 : 3.

3 : 2.

1 : 2.

Ans .

1 : 2.

Explanation :
Radius of incircle = (x/2)
Radius of circum circle= ($\sqrt{2}$x/2) =(x/$\sqrt{2}$)
Required ratio = (($\frac{\prod r^2}{4}$ ) : (($\frac{\prod r^2}{2}$ ) = (1/4) : (1/2) = 1 : 2.

Q.69

If the radius of a circle is decreased by 50%, find the percentage decrease

in its area.

85%

75%

70%

80%

Ans .

75%

Explanation :
Let original radius = R. New radius =(50/100) R = (R/2)
Original area=$\prod {r/2}^2$= and new area= $\prod {r/2}^2$= (($\frac{\prod r^2}{4}$ )
Decrease in area =((3$\frac{\prod r^2}{4}$ ) X (1/$\prod {r/2}^2$ X 100) % = 75%

Q.70

Find the volume and surface area of a cuboid 16 m long, 14 m broad and 7 m high.

768 $cm^2$

668 $cm^2$

868 $cm^2$

568 $cm^2$

Ans .

868 $cm^2$

Explanation :
Volume = (16 x 14 x 7) $m^3$ = 1568 $m^3$ Surface area = [2 (16 x 14 + 14 x 7 + 16 x 7)] $cm^2$ = (2 x 434) $cm^2$= 868 $cm^2$.

Q.71

Find the length of the longest pole that can be placed in a room 12 m long

8m broad and 9m high.

16 m.

17 m.

15 m.

13 m.

Ans .

17 m.

Explanation :
Length of longest pole = Length of the diagonal of the room
= $\sqrt{12^{2}+8^{2}+9^{2}}$= .$\sqrt{289}$= 17 m.

Q.72

Tbe volume of a wall, 5 times as high as it is broad and 8 times as long as

it is high, is 12.8 cu. metres. Find the breadth of the wall.

50 cm

40 cm

30 cm

20 cm

Ans .

40 cm

Explanation :
Let the breadth of the wall be x metres.
Then, Height = 5x metres and Length = 40x metres.
x * 5x * 40x = 12.8 --> $x^3$=12.8/200 = 128/2000 = 64/1000
So, x = (4/10) m =((4/10)*100)cm = 40 cm

Q.73

Find the number of bricks, each measuring 24 cm x 12 cm x 8 cm, required to

construct a wall 24 m long, 8m high and 60 cm thick, if 10% of the wall is filled with mortar?

45000.

55000.

50000.

35000.

Ans .

45000.

Explanation :
Volume of the wall = (2400 x 800 x 60) cu. cm.
Volume of bricks = 90% of the volume of the wall
=((90/100)*2400 *800 * 60)cu.cm.
Volume of 1 brick = (24 x 12 x 8) cu. cm.
Number of bricks=(90/100)*(2400*800*60)/(24*12*8)=45000.

Q.74

Water flows into a tank 200 m x 160 m througb a rectangular pipe of

1.5m x 1.25 m @ 20 kmph . In what time (in minutes) will the water rise by 2 metres?

94min

95min

93min

96min

Ans .

96min

Explanation :
Volume required in the tank = (200 x 150 x 2) $x^3$ = 60000 $x^3$
Length of water column flown in1 min =(20*1000)/60 m =1000/3 m
Volume flown per minute = 1.5 * 1.25 * (1000/3) $x^3$ = 625 $x^3$
Required time = (60000/625)min = 96min

Q.75

Tbe dimensions of an open box are 50 cm, 40 cm and 23 cm. Its thickness is

2 cm. If 1 cubic cm of metal used in the box weighs 0.5 gms, find the weight of the box.

7.84 kg.

8.04 kg.

8.56 kg.

8.44 kg.

Ans .

8.04 kg.

Explanation :
Volume of the metal used in the box = External Volume - Internal Volume
= [(50 * 40 * 23) - (44 * 34 * 20)]$cm^3$
= 16080 $cm^3$
Weight of the metal =((16080*0.5)/1000) kg = 8.04 kg.

Q.76

The diagonal of a cube is 63cm. Find its volume and surface area.

225 $cm^2$

116 $cm^2$

210 $cm^2$

216 $cm^2$

Ans .

216 $cm^2$

Explanation :
Let the edge of the cube be a.
$\sqrt{3}$a = 6../3 _ a = 6.
So,Volume = $a^3$ = (6 x 6 x 6) cm3 = 216 $cm^3$
Surface area = 6$a^2$ = (6 x 6 x 6) $cm^2$== 216 $cm^2$

Q.77

The surface area of a cube is 1734 sq. cm. Find its volume.

5913 $cm^3$.

4913 $cm^3$.

3913 $cm^3$.

4900 $cm^3$.

Ans .

4913 $cm^3$.

Explanation :
Let the edge of the cube bea. Then,
6$a^2$ = 1734 $a^2$ = 289 => a = 17 cm.
Volume = $a^3$= (17)3 $cm^3$= 4913 $cm^3$.

Q.78

A rectangular block 6 cm by 12 cm by 15 cm is cut up into an exact number of

equal cubes. Find the least possible number of cubes.

36.

40.

39.

Ans .

40.

Explanation :
Volume of the block = (6 x 12 x 15)$cm^3$. = 1080$cm^3$.
Side of the largest cube = H.C.F. of 6 cm, 12 cm, 15 cm = 3 cm.
Volume of this cube = (3 x 3 x 3) $cm^3$. = 27 $cm^3$..
Number of cubes = 1080/27 = 40.

Q.79

A cube of edge 15 cm is immersed completely in a rectangular vessel

containing water . If the dimensions of the base of vessel are 20 cm x 15 cm, find the rise in water level.

10.50 cm

11.25 cm

10.25 cm

11.76 cm

Ans .

11.25 cm

Explanation :
Increase in volume = Volume of the cube = (15 x 15 x 15)$cm^3$.
Rise in water level = volume/area = (15 x 15 x 15)/(20 x 15) cm = 11.25 cm.

Q.80

Three solid cubes of sides 1 cm, 6 cm and 8 cm are melted to form a new

cube. Find the surface area of the cube so formed.

486 $cm^2$

586 $cm^2$

466 $cm^2$

476 $cm^2$

Ans .

486 $cm^2$

Explanation :
Volume of new cube = ($1^3$ +$6^3$ + $8^3$) cm = 729 $cm^3$
Edge of new cube = $\sqrt[3]{729}$cm = 9 cm.
Surface area of the new cube = (6 x 9 x 9) $cm^2$ = 486 $cm^2$.

Q.81

If each edge of a cube is increased by 50%, find the percentage increase in

Its surface area.

120%

115%

125%

135%

Ans .

125%

Explanation :
Let original length of each edge = a.
Then, original surface area = 6$a$ .
New edge = (150% of a) = (150a/100) = 3a/2
New surface area = 6x ${(3a/2)}^2$ = 27 $a^2$/2
Increase percent in surface area =( $\frac{15a^2}{2}$ x $\frac{1}{6a^2}$ x 100)% = 125%

Q.82

Two cubes have their volumes in the ratio 1 : 27. Find the ratio of their

surface areas.

1:6

1:7

1:9

1:8

Ans .

1:9

Explanation :
Let their edges be a and b. Then,
$a^3$./$b^3$= 1/27 (or) ${(a/b)}^3$ = ${(1/3)}^3$ (or) (a/b) = (1/3).
Ratio of their surface area = 6$a^2$/6$b^2$ = $a^2$/$b^2$ = ${(a/b)}^2$ = 1/9, i.e. 1:9.

Q.83

Find the volume , curved surface area and the total surface area of a cylinder

with diameter of base 7 cm and height 40 cm.

987 $cm^2$

857 $cm^2$

957 $cm^2$

897 $cm^2$

Ans .

957 $cm^2$

Explanation :
Volume = $\prod r^{2}$h = ((22/7)x(7/2)x(7/2)x40) = 1540 $cm^3$. .
Curved surface area = 2$\prod$rh = (2x(22/7)x(7/2)x40)= 880 $cm^2$.
Total surface area = 2$\prod$rh + 2$\prod r^{2}$ = 2$\prod$r (h + r)
= (2 x (22/7) x (7/2) x (40+3.5)) $cm^2$= 957 $cm^2$.

Q.84

If the capacity of a cylindrical tank is 1848 m3 and the diameter of its base

is 14 m, then find the depth of the tank.

11 m

13 m

12 m

14 m

Ans .

12 m

Explanation :
Let the depth of the tank be h metres. Then,
$\prod$ x $7^2$ x h = 1848 --> h = (1848 x (7/22) x (1/49) = 12 m

Q.85

2.2 cubic dm of lead is to be drawn into a cylindrical wire 0.50 cm

diameter. Find the length of the wire in metres.

112 m.

110 m.

111 m.

122 m.

Ans .

112 m.

Explanation :
Let the length of the wire be h metres. Then,
$\prod {(0.50/(2 x 100))}^2$ x h = 2.2/1000
h = ( (2.2/1000) x (100 x 100)/(0.25 x 0.25) x (7/22) ) = 112 m.

Q.86

How many iron rods, each of length 7 m and diameter 2 cm can be made

out of 0.88 cubic metre of iron?

450

300

400

350

Ans .

400

Explanation :
Volume of 1 rod = (( 22/7) x (1/100) x (1/100) x 7 ) cu.m = 11/5000 cu.m
Volume of iron = 0.88 cu. m.
Number of rods = (0.88 x 5000/11) = 400.

Q.87

The radii of two cylinders are in the ratio 3: 5 and their heights are in tbe

ratio of 2 : 3. Find the ratio of their curved surface areas

2.5

2.0

1.5

3.0

Ans .

2.5

Explanation :
Let the radii of the cylinders be 3x, 5x and their heights be 2y, 3y respectively. Then
Ratio of their curved surface area = $\frac{2\prod X 3x X 2y}{2\prod X 5x X 3y}$ = 2/5 = 2.5

Q.88

If 1 cubic cm of cast iron weighs 21 gms, then find the eight of a cast iron

pipe of length 1 metre with a bore of 3 cm and in which thickness of the metal is 1cm.

28.3 kg.

26.4 kg.

23.8 kg.

25.14 kg.

Ans .

26.4 kg.

Explanation :
Inner radius = (3/2) cm = 1.5 cm, Outer radius = (1.5 + 1) = 2.5 cm.
Volume of iron = [$\prod$x (2.5)2 x 100 -$\prod$ x (1.5)2 x 100] $cm^{3}$
= (22/7) x 100 x [(2.5)2 - (1.5)2] $cm^{3}$
= (8800/7) $cm^{3}$
Weight of the pipe = ((8800/7) x (21/1000))kg = 26.4 kg.

Q.89

Find the slant height, volume, curved surface area and the whole surface

area of a cone of radius 21 cm and height 28 cm.

45cm

30cm

25cm

35cm

Ans .

35cm

Explanation :
Here, r = 21 cm and h = 28 cm.
Slant height, l = $\sqrt{r^{2}+h^{2}}$ = $\sqrt{21^{2}+28^{2}}$ =$\sqrt{1225}$ = 35cm

Q.90

Find the length of canvas 1.25 m wide required to build a conical tent of

base radius 7 metres and height 24 metres

340 m.

460 m.

400 m.

440 m.

Ans .

440 m.

Explanation :
Here, r = 7m and h = 24 m.
So,l = $\sqrt{r^{2}+h^{2}}$ =$\sqrt{7^{2}+24^{2}}$ =$\sqrt{625}$ = 25 m.
Area of canvas =$\prod$rl=((22/7)*7*25) $m^{2}$= 550 $m^{2}$.
Length of canvas = (Area/Width) = (550/1.25) m = 440 m.

Q.91

The heights of two right circular cones are in the ratio 1 : 2 and the

perimeters of their bases are in the ratio 3 : 4. Find the ratio of their volumes.

10 : 37

7 : 22

11 : 35

9 : 32

Ans .

9 : 32

Explanation :
Let the radii of their bases be r and R and their heights be h and 2h respectively.
Then,(2$\prod$r/2$\prod$R)=(3/4)--> R=(4/3)r.
Ratio of volumes = (((1/3)$\prod$ $r^{2}$h)/((1/3)$\prod$${4/3r}^2$(2h)))=9 : 32.

Q.92

The radii of the bases of a cylinder and a cone are in the ratio of 3 : 4 and It

heights are in the ratio 2 : 3. Find the ratio of their volumes.

7 : 8.

8 : 5.

9 : 8.

7 : 4

Ans .

9 : 8.

Explanation :
Let the radii of the cylinder and the cone be 3r and 4r and their heights be 2h and
3h respectively.
$\frac{Volume of cylinder}{Volume of cone}$ =$\frac{\prod3 r^{2}* 2h}{(1/3)\prod r^{2}* 3h} $= 9/8 = 9 : 8.

Q.93

A conical vessel, whose internal radius is 12 cm and height 50 cm, is full of

liquid. The contents are emptied into a cylindrical vessel with internal radius 10 cm.

Find the height to which the liquid rises in the cylindrical vessel

24 cm

29 cm

34 cm

26 cm

Ans .

24 cm

Explanation :
Volume of the liquid in the cylindrical vessel
= Volume of the conical vessel
= ((1/3)* (22/7)* 12 * 12 * 50) )$cm^{3}$ = (22 *4 *12 * 50)/7 $cm^{3}$
Let the height of the liquid in the vessel be h.
Then (22/7)*10*10*h =(22*4*12*50)/7 or h = (4*12*50)/100 = 24 cm

Q.94

Find the volume and surface area of a sphere of radius 10.5 cm.

4853 $cm^{3}$,1378 $cm^{2}$

4851 $cm^{3}$,1386 $cm^{2}$

4801 $cm^{3}$,1360 $cm^{2}$

4785 $cm^{3}$,1289 $cm^{2}$

Ans .

4851 $cm^{3}$,1386 $cm^{2}$

Explanation :
Volume = (4/3)$r^{3}$ =(4/3)*(22/7)*(21/2)*(21/2)*(21/2) $cm^{3}$ = 4851 $cm^{3}$.
Surface area = 4$\prod r^{2}$ =(4*(22/7)*(21/2)*(21/2)) $cm^{2}$ = 1386 $cm^{2}$

Q.95

If the radius of a sphere is increased by 50%, find the increase percent in

volume and the increase percent in the surface area

245.5%, 130%.

222%, 120%.

237.5%, 125%.

235%, 125%.

Ans .

237.5%, 125%.

Explanation :
Let original radius = R. Then, new radius = (150/100)R=(3R/2)
Original volume = (4/3)$\prod R^{3}$, New volume = (4/3)$\prod {3R/2}^{3}$ =($\prod R^{3}$/2)
Increase % in volume=((19/6)$\prod R^{3}$)*(3/4$\prod R^{3}$)*100))% = 237.5%
Original surface area =4$\prod R^{2}$. New surface area = 4$\prod {3R/2}^{2}$=9($\prod R^{2}$)
Increase % in surface area =(5$\prod R^{2}$/4$\prod R^{2}$) * 100) % = 125%.

Q.96

Find the number of lead balls, each 1 cm in diameter that can be

a sphere of diameter 12 cm.

1728.7

1776

1754

1747.6

Ans .

1728.7

Explanation :
Volume of larger sphere = (4/3)$\prod$*6*6*6) $cm^{3}$ = 288$\prod$ $cm^{3}$
Volume of 1 small lead ball = ((4/3)$\prod$*(1/2)*(1/2)*(1/2)) $cm^{3}$ = $\prod$/6 $cm^{3}$
Number of lead balls = (288$\prod$*(6/$\prod$)) = 1728.7

Q.97

How many spherical bullets can be made out of a lead cylinder 28cm high and

with radius 6 cm, each bullet being 1.5 cm in diameter ?

1776

1734

1645

1792

Ans .

1792

Explanation :
Volume of cylinder = ($\prod$ x 6 x 6 x 28 ) $cm^{3}$= ( 9$\prod$/16) $cm^{3}$.
Number of bullet =$ \frac{Volume of cylinder}{Volume of each bullet}$ = [(36 x 28)$\prod$ x 16] /9$\prod$ = 1792.

Q.98

A copper sphere of diameter 18cm is drawn into a wire of diameter 4 mm

Find the length of the wire.

343m

256m

243m

213m

Ans .

243m

Explanation :
Volume of sphere = ((4$\prod$/3) x 9 x 9 x 9 ) $cm^{3}$ = 972$\prod$$cm^{3}$
Volume of sphere = ($\prod$ x 0.2 x 0.2 x h ) $cm^{3}$
972$\prod$= $\prod$ x (2/10) x (2/10) x h --> h = (972 x 5 x 5 )cm = [( 972 x 5 x5 )/100 ] m
= 243m

Q.99

Two metallic right circular cones having their heights 4.1 cm and 4.3 cm and

the radii of their bases 2.1 cm each, have been melted together and recast into a

sphere. Find the diameter of the sphere.

3.5.cm

4.2.cm

3.4.cm

4.7.cm

Ans .

4.2.cm

Explanation :
Volume of sphere = Volume of 2 cones
= ($ \frac{1}{3}\prod$x (2.102) x 4.1 + $ \frac{1}{3} \prod x {2.1}^2 $x 4.3)
Let the radius of sphere be R
(4/3)$\prod R^{3}$ = (1/3)$\prod {2.1}^{3}$ or R = 2.1cm
Hence , diameter of the sphere = 4.2.cm

Q.100

A Cone and a sphere have equal radii and equal volumes. Find the ratio of the

sphere of the diameter of the sphere to the height of the cone.

1:7

1:2

1:3

1:5

Ans .

1:2

Explanation :
Let radius of each be R and height of the cone be H.
Then, (4/3) $\prod R^{3}$ = (1/3) $\prod R^{2}$H (or) R/H = ¼ (or) 2R/H = 2/4 =1/2
Required ratio = 1:2.

Q.101

Find the volume , curved surface area and the total surface area of a

hemisphere of radius 10.5 cm.

1039.5 $cm^{2}$

1037.5 $cm^{2}$

1041.5 $cm^{2}$

1034.5 $cm^{2}$

Ans .

1039.5 $cm^{2}$

Explanation :
Volume = (2 $\prod r^{3}$/3) = ((2/3) x (22/7) x (21/2) x (21/2) x (21/2))$cm^{3}$
= 2425.5 $cm^{3}$
Curved surface area = 2$\prod r^{3}$ = (2 x (22/7) x (21/2) x (21/2))$cm^{2}$
=693 $cm^{2}$
Total surface area = 3$\prod r^{3}$ = (3 x (22/7) x (21/2) x (21/2))$cm^{2}$
= 1039.5 $cm^{2}$.

Q.102

Hemispherical bowl of internal radius 9 cm contains a liquid. This liquid is to be filled into cylindrical shaped small bottles of diameter 3 cm

and height 4 cm. How many bottles will be needed to empty the bowl

Ans .

Explanation :
Volume of bowl = ((2($\prod $/3) x 9 x 9 x 9 ) $cm^{3}$= 486($\prod $$cm^{3}$.
Volume of 1 bottle = ($\prod $ x (3/2) x (3/2) x 4 ) $cm^{3}$ = 9($\prod $$cm^{3}$
Number of bottles = (486($\prod $/9($\prod $) = 54.

Q.103

A Cone,a hemisphere and a cylinder stand on equal bases and have the same

height.Find ratio of their volumes.

1:2:2

1:3:3

1:2:3

1:1:3

Ans .

1:2:3

Explanation :
Let R be the radius of each
Height of the hemisphere = Its radius = R.
Height of each = R.
Ratio of volumes = (1/3)$\prod R^{2}$ x R : (2/3)$\prod R^{3}$ : $\prod R^{2}$ x R = 1:2:3

Q.104

In a km race, A beats B by 28 metres or 7 seconds. Find A's timeover the course.

5 min. 6 s

3 min. 5 s

4 min. 3 s

7 min. 3 s

Ans .

4 min. 3 s

Explanation :
Clearly, B covers 28 m in 7 seconds.
B's time over the course = (278 x 1000) sec = 250 seconds.
A's time over the course = (250 - 7-) sec = 243 sec = 4 min. 3 s

Q.105

A runs 1 ¾ times as fast as B. if A gives B a start of 84 m, bow far must

winning post be so that A and B might reach it at the same time?

196 m

186 m

200 m

206 m

Ans .

196 m

Explanation :
Ratio of the rates of A and B = 7/4 : 1 = 7 : 4.
So, in a race of 7 m, A gains 3m over B.
3 m are gained by A in a race of 7 m.
84 m are gained by A in a race of (7/3 x 84) m = 196 m.
Winning post must be 196 m away from the starting point

Q.106

A can run 1 km in 3 min. 10 sec. and B can cover the same distance in 3

min. 20 sec. By what distance can A beat B ?

64 m

48 m

50 m

68 m

Ans .

50 m

Explanation :
Clearly, A beats B by 10 sec.
Distance covered by B in 10 sec. = ($\frac{1000 }{200}$x 10 )m = 50 m.
Therefore A beats B by 50 metres

Q.107

In a 100 m race, A runs at 8km per hour. If A gives B a start of 4 m and

still him by 15 seconds, what is the speed of B ?

5.13 km/hr

5.76 km/hr

4.76 km/hr

4.06 km/hr

Ans .

5.76 km/hr

Explanation :
Time taken by A to cover 100 m =(60 X 60 / 8000) x 100 sec = 45 sec.
B covers (100 - 4) m = 96 m in (45 + 15) sec = 60 sec.
B's speed =$\frac{96 *60 * 60}{60 *1000} $ km/hr = 5.76 km/hr.

Q.108

A, Band C are three contestants in a km race. If A can give B a start of 40 m

and A can give C a start of 64m how many metre's start can B give C ?

806 m

906 m

936 m

986 m

Ans .

936 m

Explanation :
While A covers 1000 m, B covers (1000 - 40) m = 960 m and
C covers (1000 - 64) m or 936 m.
When B covers 960 m, C covers 936 m.

Q.109

In a game of 80 points; A can give B 5 points and C 15 points. Then how

many points B can give C in a game of 60 ?

7 points

8 points

9 points

5 points

Ans .

8 points

Explanation :
A: B = 80 : 75, A : C = 80 : 65.
B/C = ( B/ A * A/C) = (75 / 80 * 80 / 65) = 15/13 = 60 /52 = 60: 5
Therfore ,In a game of 60, B can give C 8 points

Q.110

What was the day of the week on, 16th July, 1776?

Wednesday

Monday

Sunday

Tuesday

Ans .

Tuesday

Explanation :
16th July, 1776 = (1775 years + Period from 1st Jan., 1776 to 16th July,1776)
Counting of odd days :
1600 years have 0 odd day. 100 years have 5 odd days.
75 years = (18 leap years + 57 ordinary years)
= [(18 x 2) + (57 x 1)] odd days = 93 odd days
= (13 weeks + 2 days) = 2 odd days.
1775 years have (0 + 5 + 2) odd days = 7 odd days = 0 odd day.
Jan. Feb. March April May June July
31 + 29 + 31 + 30 + 31 + 30 +16 = 198days
= (28 weeks + 2 days) =2days
Total number of odd days = (0 + 2) = 2. Required day was 'Tuesday'.

Q.111

What was the day of the week on 16th August, 1947?

Sunday

Saturday

Monday

Friday

Ans .

Saturday

Explanation :
15th August, 1947 = (1946 years + Period from 1st Jan., 1947 to 15th
Counting of odd days:
1600 years have 0 odd day. 300 years have 1 odd day.
47 years = (11 leap years + 36 ordinary years)
= [(11 x 2) + (36 x 1») odd days = 58 odd days = 2 odd days.
Jan. Feb. March April May June July Aug.
31 + 28 + 31 + 30 + 31 + 30 + 31 + 15
= 227 days = (32 weeks + 3 days) = 3,
Total number of odd days = (0 + 1 + 2 + 3) odd days = 6 odd days.
Hence, the required day was 'Saturday'.

Q.112

What was the day of the week on 16th April, 2000 ?

Sunday

Saturday

Friday

Monday

Ans .

Sunday

Explanation :
16th April, 2000 = (1999 years + Period from 1st Jan., 2000 to 16thA'
Counting of odd days:
1600 years have 0 odd day. 300 years have 1 odd day.
99 years = (24 leap years + 75 ordinary years)
= [(24 x 2) + (75 x 1)] odd days = 123 odd days
= (17 weeks + 4 days) = 4 odd days.
Jan. Feb. March April
31 + 29 + 31 + 16 = 107 days = (15 weeks + 2 days) = 2 odd,
Total number of odd days = (0 + 1 + 4 + 2) odd days = 7 odd days = 0 oddday.
Hence, the required day was 'Sunday'.

Q.113

On what dates of Jull.2004 did Monday fall?

6th, 13th, 20th and 27th

5th, 12th, 19th and 26th

4th, 11th, 18th and 25th

3th, 10th, 17th and 24th

Ans .

5th, 12th, 19th and 26th

Explanation :
Let us find the day on 1st July, 2004.
2000 years have 0 odd day. 3 ordinary years have 3 odd days.
Jan. Feb. March April May June July
31 + 29 + 31 + 30 + 31 + 30 + 1
= 183 days = (26 weeks + 1 day) = 1 t .
Total number of odd days = (0 + 3 + 1) odd days = 4 odd days. '
1st July 2004 was 'Thursday',-,-
Thus, 1st Monday in July 2004 _as on 5th July.
Hence, during July 2004, Monday fell on 5th, 12th, 19th and 26th.

Q.114

Find the angle between the hour hand and the minute hand of a clock when 3.25

29°

23°

49°

47*1/2°

Ans .

47*1/2°

Explanation :
angle traced by the hour hand in 12 hours = 360°
Angle traced by it in three hours 25 min (ie) 41/12 hrs=(360*41/12*12)°
=102*1/2°
angle traced by minute hand in 60 min. = 360°.
Angle traced by it in 25 min. = (360 X 25 )/60= 150°
Required angle = 1500 – 102*1/2°= 47*1/2°

Q.115

At what time between 2 and 3 o'clock will the hands of a clock be together?

110/13 min. past 8

12/11 min. past 28

120/11 min. past 2

12/19 min. past 20

Ans .

120/11 min. past 2

Explanation :
At 2 o'clock, the hour hand is at 2 and the minute hand is at 12, i.e. they
are 10 min spaces apart.
To be together, the minute hand must gain 10 minutes over the hour hand.
Now, 55 minutes are gained by it in 60 min.
10 minutes will be gained in (60 x 10)/55 min. = 120/11 min.
The hands will coincide at 120/11 min. past 2.

Q.116

At what time between 4 and 5 o'clock will the hands of a clock be at right angle?

53/11 min. past 14

4/11 min. past 40

40/41 min. past 7

40/11 min. past 4

Ans .

paste right option

Explanation :
At 4 o'clock, the minute hand will be 20 min. spaces behind the hour hand,
Now, when the two hands are at right angles, they are 15 min. spaces apart. So,
they are at right angles in following two cases.
Case I. When minute hand is 15 min. spaces behind the hour hand:
In this case min. hand will have to gain (20 - 15) = 5 minute spaces. 55 min. spaces are gained by it in 60 min.
5 min spaces will be gained by it in 60*5/55 min=60/11min.
They are at right angles at 60/11min. past 4.
Case II. When the minute hand is 15 min. spaces ahead of the hour hand:
To be in this position, the minute hand will have to gain (20 + 15) = 35 minute spa' 55 min. spaces are gained in 60 min.
35 min spaces are gained in (60 x 35)/55 min =40/11
They are at right angles at 40/11 min. past 4

Q.117

Find at what time between 8 and 9 o'clock will the hands of a clock

being the same straight line but not together.

120/11 min

113/11 min

123/13 min

110/13 min

Ans .

120/11 min

Explanation :
At 8 o'clock, the hour hand is at 8 and the minute hand is at 12, i.e. the two
hands_ are 20 min. spaces apart.
To be in the same straight line but not together they will be 30 minute spaces apart.
So, the minute hand will have to gain (30 - 20) = 10 minute spaces over the hour hand.
55 minute spaces are gained. in 60 min.
10 minute spaces will be gained in (60 x 10)/55 min. = 120/11min.
The hands will be in the same straight line but not together at 120/11 min.

Q.119

At what time between 5 and 6 o'clock are the hands of a clock

3minapart?

36/11 min. past 9

346/11 min. past 5.

117/11 min. past 5.

316/13 min. past 5.

Ans .

346/11 min. past 5

Explanation :
At 5 o'clock, the minute hand is 25 min. spaces behind the hour hand.
Case I. Minute hand is 3 min. spaces behind the hour hand.
In this case, the minute hand has to gain' (25 - 3) = 22 minute spaces. 55 min. are
gained in 60 min.
22 min. are gaineg in (60*22)/55min. = 24 min.
The hands will be 3 min. apart at 24 min. past 5.
Case II. Minute hand is 3 min. spaces ahead of the hour hand.
In this case, the minute hand has to gain (25 + 3) = 28 minute spaces. 55 min. are gained in 60 min.
28 min. are gained in (60 x 28_)/55=346/11
The hands will be 3 min. apart at 346/11 min. past 5.

Q.120

The minute hand of a clock overtakes the hour hand at intervals of 65

minutes of the correct time. How much a day does the clock gain or lose?

140/43 minutes

410/42 minutes

450/41 minutes

440/43 minutes

Ans .

440/43 minutes

Explanation :
In a correct clock, the minute hand gains 55 min. spaces over the hour hand in 60 minutes.
To be together again, the minute hand must gain 60 minutes over the hour hand. 55 min. are gained in 60 min.
60 min are gained in (60/55) x 60 min =720/11 min.
But, they are together after 65 min.
Gain in 65 min =720/11-65 =5/11min.
Gain in 24 hours =(5/11 * (60*24)/65)min =440/43
The clock gains 440/43 minutes in 24 hours.

Q.121

A watch which gains uniformly, is 6 min. slow at 8 o'clock in the

morning Sunday and it is 6 min. 48 sec. fast at 8 p.m. on following Sunday.

When was it correct?

Wednesday

Friday

Thursday

Tuesday

Ans .

Wednesday

Explanation :
Time from 8 a.m. on Sunday to 8 p.m. on following Sunday = 7 days 12 hours = 180 hours
The watch gains (5 + 29/5) min. or 54/5 min. in 180 hrs.
Now 54/5 min. are gained in 180 hrs.
5 min. are gained in (180 x 5/54 x 5) hrs. = 83 hrs 20 min. = 3 days 11 hrs 20 min.
Watch is correct 3 days 11 hrs 20 min. after 8 a.m. of Sunday.
It will be correct at 20 min. past 7 p.m. on Wednesday

Q.122

A clock is set right at 6 a.m. The clock loses 16 minutes in 24 hours.

What will be the true time when the clock indicates 10 p.m. on 4th day?

1 a.m

12 p.m

11 p.m

2 a.m

Ans .

11 p.m

Explanation :
Time from 5 a.m. on a day to 10 p.m. on 4th day = 89 hours.
Now 23 hrs 44 min. of this clock = 24 hours of correct clock.
356/15 hrs of this clock = 24 hours of correct clock.
89 hrs of this clock = (24 x 31556 x 89) hrs of correct clock.
= 90 hrs of correct clock.
So, the correct time is 11 p.m.

Q.123

A clock is set right at 8 a.m. The clock gains 10 minutes in 24 hours will

be the true time when the clock indicates 1 p.m. on the following day?

36 min. past 11

25 min. past 8

48 min. past 12

36 min. past 18

Ans .

48 min. past 12

Explanation :
Time from 8 a.m. on a day 1 p.m. on the following day = 29 hours.
24 hours 10 min. of this clock = 24 hours of the correct clock.
145 /6 hrs of this clock = 24 hrs of the correct clock
29 hrs of this clock = (24 x 6/145 x 29) hrs of the correct clock
= 28 hrs 48 min. of correct clock
The correct time is 28 hrs 48 min. after 8 a.m.
This is 48 min. past 12.

Q.124

Find the cost of:

(i) Rs. 7200, 8% stock at 90;

(ii) Rs. 4500, 8.5% stock at 4 premium;

(iii) Rs. 6400, 10% stock at 15 discount.

Rs. 6480.,Rs. 4680,Rs. 5440

Rs. 6440.,Rs. 4660,Rs. 5440

Rs. 6560.,Rs. 4120,Rs. 5340

Rs. 6320.,Rs. 3680,Rs. 4440

Ans .

Rs. 6480.,Rs. 4680,Rs. 5440

Explanation :
(i) Cost of Rs. 100 stock = Rs. 90
Cost of Rs. 7200 stock = Rs. (90/100 * 7200 ) = Rs. 6480.
(ii) Cost of Rs. 100 stock = Rs. (100+4)
Cost of Rs. 4500 stock = Rs. (104/100 * 4500 ) = Rs. 4680
(iii) Cost of Rs. 100 stock = Rs. (100-15)
Cost of Rs. 6400 stock = Rs. (85/100 * 6400 ) = Rs. 5440.

Q.125

Find the cash required to purchase Rs. 3200, 7(1/2) % stock at 107

(brokerage (1/2) %)

Rs. (115/2),Rs. 1140

Rs. (215/2),Rs. 3440

Rs. (215/2),Rs. 1440

Rs. (315/2),Rs. 4440

Ans .

Rs. (215/2),Rs. 3440

Explanation :
Cash required to purchase Rs. 100 stock = Rs (107+(1/2)) = Rs. (215/2).
Cash required to purchase Rs. 100 stock = Rs [(215/2)*(1/100)*3200] = Rs. 3440

Q.126

Find the cash realised by selling Rs. 2440, 9.5% stock at 4 discount

(brokerage (1/4) %)

Rs. (324/4),Rs 2198

Rs. (383/4),Rs 2298

Rs. (313/4),Rs 1298

Rs. (333/7),Rs 2228

Ans .

Rs. (383/4),Rs 2298

Explanation :
By selling Rs. 100 stock , cash realised = Rs. [(100-4)-(1/4)] = Rs. (383/4).
By selling Rs. 2400 stock, cash realised = Rs. [(383/4)*(1/100)*2400] = Rs 2298.

Q.127

Find the annual income derived from Rs. 2500, 8% stock at 106.

Rs. 300

Rs. 200

Rs. 150

Rs. 250

Ans .

Rs. 200

Explanation :
Income from Rs. 100 stock = Rs. 8.
Income from Rs. 2500 = Rs. [(8/1000*2500) =Rs. 200.

Q.128

Find the annual income derived by investing Rs. 6800 in 10% stock at 136.

Rs. 300

Rs. 600

Rs. 400

Rs. 500

Ans .

Rs. 500

Explanation :
By investing Rs. 136, income obtained = Rs. 10.
By investing Rs. 6800, income obtained = Rs. [(10/136)*6800] = Rs. 500.

Q.129

Which is better investment? 7(1/2) % stock at 105 or 6(1/2) % at 94.

7(1/2) % stock at 105 is better

6(1/2) % at 94 is better

7(1/2) % stock at 105 and 6(1/2) % at 94 is better

none of them

Ans .

7(1/2) % stock at 105 is better

Explanation :
Let the investment in each case be Rs. (105*94).
Case I : 7(1/2) 5 stock at 105:
On investing Rs. 105, income = Rs. (15/2).
On investing Rs. (105*94), income = Rs. [(15/2)*(1/105)*105*94] = Rs 705.
Case II : 6(1/2) % stock at 94:
On investing Rs. 94, income = Rs. (13/2).
On investing Rs. (105*94), income = Rs. [(13/2)*(1/94)*105*94] = Rs. 682.5.
Clearly, the income from 7(1/2) % stock at 105 is more.
Hence, the investment in 7(1/2) % stock at 105 is better.

Q.130

Find the cost of 96 shares of Rs. 10 each at (3/4) discount, brokerage being

(1/4) per share.

Rs. 812

Rs. 912

Rs. 921

Rs. 902

cAns .

Rs. 912

Explanation :
Cost of 1 share = Rs. [(10-(3/4)) + (1/4)] = Rs. (19/2).
Cost of 96 shares = Rs. [(19/2)*96] = Rs. 912.

Q.131

Find the income derived from 88 shares of Rs. 25 each at 5 premium,

brokerage being (1/4) per share and the rate of dividend being 7(1/2) % per annum.

Also, find the rate of interest on the investment.

Rs. 165, 6.2 %

Rs. 155, 5.5 %

Rs. 175, 7.2%

Rs. 150, 5.6%

Ans .

Rs. 165, 6.2 %

Explanation :
Cost of 1 share = Rs. [25+5+1/4)] = Rs. (121/4).
Cost of 88 shares = Rs.[(121/4)*88] = Rs. 2662.
Investment made = Rs. 2662.
Face value of 88 shares = Rs. (88*25) = Rs. 2200.
Dividend on Rs. 100 = (15/2).
Dividend on Rs. 2200 = Rs. [(15/20*(1/100)*2200] = Rs. 165.
Income derived = Rs. 165.
Rate of interest on investment = [(165/2662)*100] = 6.2 %.

Q.132

A man buys Rs. 25 shares in company which pays 9 % dividend. The

money invested is such that it gives 10 % on investment. At what price did he buy

the shares?

Rs. 32.50

Rs. 25.50

Rs. 22.50

Rs. 35.50

Ans .

Rs. 22.50

Explanation :
Suppose he buys each share for Rs. x.
Then, [25*(9/100)] = [x*(10/100)] or x = Rs. 22.50.
Cost of each share = Rs. 22.50.

Q.134

A man sells Rs.5000, 12 % stock at 156 and uinvests the proceeds parity in

8 % stock at 90 and 9 % stock at 108. He hereby increases his income by Rs. 70.

How much of the proceeds were invested in each stock?

Rs. 4500.

Rs. 3500.

Rs. 3800.

Rs. 4200.

Ans .

Rs. 4200.

Explanation :
S.P of Rs. 5000 stock = Rs. [(156/100)*5000] = Rs. 7800.
Income from this stock = Rs. [(12/100)*5000] = Rs. 600.
Let investment in * % stock be x and that in 9 % stock = (7800-x).
[x*(8/90)] + (7800-x) * (9/108) = (600+7)
(4x/45) + [(7800-x)/12] = 670 -->16x + 117000-15x = (670*180) --> x = 3600.
Money invested in 8 % stock at 90 = Rs. 3600.
Money invested in 9 % at 108 = Rs. (7800-3600) = Rs. 4200.

Q.135

Evaluate: 30!/28!

770

870

850

800

Ans .

870

Explanation :
We have, 30!/28! = 30x29x(28!)/28! = (30x29) = 870.

Q.136

Find the value of (i) $_{60}^{3}\textrm{P}$ (ii) $_{4}^{4}\textrm{P}$

205320,24

205408,32

205439,30

205310,24

Ans .

205320,24

Explanation :
(i) $_{60}^{3}\textrm{P}$ = 60!/(60-3)! = 60!/57! = 60x59x58x(57!)/57! = (60x59x58) = 205320.
(ii) $_{4}^{4}\textrm{P}$ = 4! = (4x3x2x1) = 24.

Q.137

Find the vale of (i) $_{8}^{10}\textrm{C}$ (ii)$_{98}^{100}\textrm{C}$ (iii) $_{50}^{50}\textrm{C}$

110,4550,1

120,4950,1

120,5050,0

100,5250,0

Ans .

120,4950,1

Explanation :
(i) $_{8}^{10}\textrm{C}$ = $\frac{10*9*8}{3!}$ = 120.
(ii) $_{98}^{100}\textrm{C}$=$_{(100-98)}^{100}\textrm{C}$ = $\frac{100*99}{2!}$ = 4950.
(iii) $_{50}^{50}\textrm{C}$= 1. [$_{n}^{n}\textrm{C}$ = 1]

Q.138

How many words can be formed by using all letters of the word “BIHAR”

110

100

120

Ans .

120

Explanation :
The word BIHAR contains 5 different letters.
Required number of words = $_{5}^{5}\textrm{P}$ = 5! = (5x4x3x2x1) = 120.

Q.139

How many words can be formed by using all letters of the word ‘DAUGHTER’ so

that the vowels always come together?

4320

4110

3370

2350

Ans .

4320

Explanation :
Given word contains 8 different letters. When the vowels AUE are always together,
we may suppose them to form an entity, treated as one letter.
Then, the letters to be arranged are DGNTR (AUE).
Then 6 letters to be arranged in $_{6}^{6}\textrm{P}$ = 6! = 720 ways.
The vowels in the group (AUE) may be arranged in 3! = 6 ways.
Required number of words = (720x6) = 4320.

Q.140

How many words can be formed from the letters of the word ‘EXTRA’ so that the

vowels are never together?

126

118

110

Ans .

Explanation :
The given word contains 5 different letters.
Taking the vowels EA together, we treat them as one letter.
Then, the letters to be arranged are XTR (EA).
These letters can be arranged in 4! = 24 ways.
The vowels EA may be arranged amongst themselves in 2! = 2 ways.
Number of words, each having vowels together = (24x2) = 48 ways.
Total number of words formed by using all the letters of the given words
= 5! = (5x4x3x2x1) = 120.
Number of words, each having vowels never together = (120-48) = 72.

Q.141

How many words can be formed from the letters of the word ‘DIRECTOR’

So that the vowels are always together?

2060

1180

2110

2160

Ans .

2160

Explanation :
In the given word, we treat the vowels IEO as one letter.
Thus, we have DRCTR (IEO).
This group has 6 letters of which R occurs 2 times and others are different.
Number of ways of arranging these letters = 6!/2! = 360.
Now 3 vowels can be arranged among themselves in 3! = 6 ways.
Required number of ways = (360x6) = 2160.

Q.142

In how many ways can a cricket eleven be chosen out of a batch of

15 players ?

1365

1330

1265

1225

Ans .

1365

Explanation :
Required number of ways = $_{11}^{15}\textrm{C}$ = $_{(15-11)}^{15}\textrm{C}$ = $_{4}^{11}\textrm{C}$
= $\frac{15*14*13*12}{4*3*2*1}$ = 1365.

Q.143

In how many ways, a committee of 5 members can be selected from

6 men and 5 ladies, consisting of 3 men and 2 ladies?

100

210

200

110

Ans .

200

Explanation :
(3 men out 6) and (2 ladies out of 5) are to be chosen.
Required number of ways = ($_{3}^{6}\textrm{C}$x$_{2}^{5}\textrm{C}$) = [$\frac{6*5*4}{3*2*1}$] x [$\frac{5*4}{2*1}$] = 200

Q.144

In a throw of a coin ,find the probability of getting a head

1/5

1/3

1/2

Ans .

1/2

Explanation :
Here s={H,T} and E={H}.
P(E)=n(E)/n(S)=1/2

Q.145

Two unbiased coin are tossed .what is the probability of getting atmost

one head?

3/4

3/2

1/4

1/2

Ans .

3/4

Explanation :
Here S={HH,HT,TH,TT}
Let Ee=event of getting one head
E={TT,HT,TH}
P(E)=n(E)/n(S)=3/4

Q.146

An unbiased die is tossed .find the probability of getting a multiple of 3

1/2

1/5

1/3

Ans .

1/3

Explanation :
Here S={1,2,3,4,5,6}
Let E be the event of getting the multiple of 3
then ,E={3,6}
P(E)=n(E)/n(S)=2/6=1/3

Q.147

In a simultaneous throw of pair of dice .find the probability of getting

the total more than 7

5/13

11/12

5/11

5/12

Ans .

5/12

Explanation :
Here n(S)=(6*6)=36
let E=event of getting a total more than 7
={(2,6),(3,5),(3,6),(4,4),(4,5),(4,6),(5,3),(5,4),(5,5),(5,6),(6,2),(6,3),(6,4),(6,5),(6,6)}
P(E)=n(E)/n(S)=15/36=5/12.

Q.148

A bag contains 6 white and 4 black balls .2 balls are drawn at random.

find the probability that they are of same colour.

7/11

7/15

2/15

3/11

Ans .

7/15

Explanation :
.let S be the sample space
Then n(S)=no of ways of drawing 2 balls out of (6+4)=($_{2}^{10}\textrm{C}$=(10*9)/(2*1)=45
Let E=event of getting both balls of same colour
Then n(E)=no of ways(2 balls out of six) or(2 balls out of 4)
=(($_{2}^{6}\textrm{C}$+($_{2}^{4}\textrm{C}$)=(6*5)/(2*1)+(4*3)/(2*1)=15+6=21
P(E)=n(E)/n(S)=21/45=7/15

Q.149

Two dice are thrown together .What is the probability that the sum of the

number on the two faces is divided by 4 or 6

5/13

7/11

7/18

2/3

Ans .

7/18

Explanation :
Clearly n(S)=6*6=36
Let E be the event that the sum of the numbers on the two faces is divided by
4 or 6.Then
E={(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(6,2),(6,6)}
n(E)=14.
Hence p(e)=n(e)/n(s)=14/36=7/18

Q.150

Two cards are drawn at random from a pack of 52 cards.what is the

probability that either both are black or both are queen?

5/11

55/21

2/11

55/221

Ans .

55/221

Explanation :
We have n(s)=52c2=(52*51)/(2*1)=1326.
Let A=event of getting both black cards
B=event of getting both queens
A$\cap$B=event of getting queen of black cards
n(A)= ($_{2}^{26}\textrm{C}$=(26*25)/(2*1)=325,
n(B)= ($_{2}^{4}\textrm{C}$=(4*3)/(2*1)=6 and
n(A$\cap$B)= ($_{2}^{2}\textrm{C}$=1
P(A)=n(A)/n(S)=325/1326;
P(B)=n(B)/n(S)=6/1326 and
P(A$\cap$B)=n(A$\cap$B)/n(S)=1/1326
P(A$\cap$B)=P(A)+P(B)-P(A$\cap$B)=(325+6-1/1326)=330/1326=55/221.

Q.151

Find the present worth of Rs. 930 due 3 years hence at

8% per annum. Also find the discount.

Rs. 180

Rs. 102

Rs. 192

Rs. 132

Ans .

Rs. 180

Explanation :
P.W=100 x Amount /[100 + (R x T)]
=Rs.100 x 930/100+ (8x3)
= (100x930)/124= Rs. 750,
T.D. = (Amount) - (P.W.) = Rs. (930 - 750) = Rs. 180.

Q.152

The true discount on a bill due 9 months hence at 12%

per annum is Rs. Find the amount of the bill and its present worth..

Rs. 5000

Rs. 4500

Rs. 6000

Rs.5500

Ans .

Rs. 6000

Explanation :
Let amount be Rs. x.
Then,x*R*T/100 + (R x T)
=T.D.=>x*12*(3/ 4)/[100+[12*3/4]]=540
x= 540x109 = Rs.6540
Amount - Rs. 6540. P.W. = Rs. (6540 - 540) - Rs. 6000..

Q.153

The true discount on a certain sum of money due 3 years

hence is Rb. 250 and the simple interest on the same sum for the same time and

at the same rate is Rs. 375. Find the sumand the rate percent.

16 2/3%.

16 1/5%.

11 5/3%.

13 1/3%.

Ans .

16 2/3%.

Explanation :
T.D. = Rs. 250 and S.I. = Rs. 375.
Sum due =S.I. xT.D./ S.I. -T.D.=375x250/375- 250=Rs.750.
Rate=[100*375/750*3]%=16 2/3%.

Q.154

The difference between the simple interest and true discount on a certain sum

of money for 6 months at 12% per annum is Rs. 25. Find the sum.

Rs.5500

Rs. 6200

Rs.5800

Rs. 6800

Ans .

Rs. 6800

Explanation :
Let the sum be Rs. x. Then,
T.D. = (x*25/2*1/2)/(100+(25/2*1/2))=x*25/4*4/425=x/17
S.I=x*25/2*1/2*1/100=x/16
x/16-x/17=25 =>17x-16x=25*16*17 =>x=6800
Hence, sum due = Rs. 6800..

Q.155

A bill falls due in 1 year. The creditor agrees to accept immediate payment of the half and to defer the payment of the

other half for 2 years. By this arrangement ins Rs. 40. What is the amount of the bill, if the money be worth 12% ?.

Rs. 3200

Rs. 3000

Rs. 3600

Rs. 3500

Ans .

Rs. 3600

Explanation :
Let the sum be Rs. x. Then,
[x/2+(x/2*100)/100+(25/2*2)]-[(x*100)/(100+25/2*1]=40
=>x/2+2x/5-8x/9=40=>x=3600
Amount of the bill - Rs. 3600

Q.156

A bill for Rs. 6000 is drawn on July 14 at 5 months. It is discounted on 5th

October at 10%. Find the banker's discount, true discount, banker's gain and the money that the holder of the bill receives

Rs. 5800

Rs. 5880

Rs. 4680

Rs. 4380

Ans .

Rs. 5880

Explanation :
Face value of the bill = Rs. 6000.
Date on which the bill was drawn = July 14 at 5 months. Nominally due date =December 14.,Legally due date = December 17.
Date on which the bill was discounted = October 5. Unexpired time : Oct. Nov. Dec.
26 + 30 + 17 = 73 days =1/ 5Years
B.D. = S.I. on Rs. 6000 for 1/5 year= Rs. (6000 x 10 x1/5 x1/100)= Rs. 120.
T.D. = Rs.[(6000 x 10 x1/5)/(100+(10*1/5))]=Rs.(12000/102)=Rs. 117.64.
B.G. = (B.D.) - (T.D.) = Rs. (120 - 117.64) = Rs. 2.36. Money received by the holder of the bill = Rs. (6000 - 120)= Rs. 5880..

Q.157

If the true discount on a certain sum due 6 months hence at 15% is Rs. 120,

what is the banker's discount on the same sum for the same time and at the same rate?

Rs. 129

Rs. 109

Rs. 125

Rs. 119

Ans .

Rs. 129

Explanation :
B.G. = S.I. on T.D.
= Rs.(120 x 15 x 1/2 x 1/100)= Rs. 9.
(B.D.) - (T.D.) = Rs. 9.
B.D. = Rs. (120 + 9) = Rs. 129.

Q.158

The banker's discount on Rs. 1800 at 12% per annum is equal to the true

discount on Rs. 1872 for the same time at the same rate. Find the time.

5 months

3 months

4 months

2 months

Ans .

4 months

Explanation :
S.I. on Rs. 1800 = T.D. on Rs. 1872.
P.W. of Rs. 1872 is Rs. 1800.
Rs. 72 is S.I. on Rs. 1800 at 12%.
Time =[(100 x 72)/ (12x1800)]year=1/3year = 4 months.

Q.159

The banker's discount and the true discount on a sum of money due 8 months

hence are Rs. 120 and Rs. 110 respectively. Find the sum and the rate percent.

13 7/11%

13 %

11 13/11%

11 17/13%

Ans .

13 7/11%

Explanation :
Sum =[( B.D.*T.D.)/(B.D.-T.D.)] = Rs.[(120x110)/(120-110)]= Rs. 1320. Since B.D. is S.I. on sum due, so S.I. on Rs. 1320 for 8 months is Rs. 120. Rate =[(100 x120)/( 1320 x 2/3)%= 13 7/11%.

Q.160

The present worth of a bill due sometime hence is Rs. 1100 and the true

discount on the bill is Rs. 110. Find the banker's discount and the banker's gain.

Rs. 111

Rs. 121

Rs. 110

Rs. 119

Ans .

Rs. 121

Explanation :
T.D. =$\sqrt{(P.W.*B.G)}$
B.G. =$\frac{(T.D.)^2}{P.W}$ = Rs.[(110x110)/ 1100]= Rs. 11.
B.D.= (T.D. + B.G.) = Rs. (110 + 11) = Rs. 121..

Q.161

The banker's discount on Rs. 1650 due a certain time hence is Rs. 165. Find

the true discount and the banker's gain.

Rs 12

Rs 11

Rs 15

Rs 13

Ans .

Rs 15

Explanation :
Sum = [(B.D.xT.D.)/ (B.D.-T.D.)]= [(B.D.xT.D.)/B.G.]
T.D./B.G. = Sum/ B.D.=1650/165=10/1
Thus, if B.G. is Re 1, T.D. = Rs. 10.
If B.D.is Rs. ll, T.D.=Rs. 10.
If B.D. is Rs. 165, T.D. = Rs. [(10/11)xl65]=Rs.150
And, B.G. = Rs. (165 - 150) = Rs 15.

Q.162

What rate percent does a man get for his money when in discounting a bill

due 10 months hence, he deducts 10% of the amount of the bill?

13 1/3%

11 1/5%

7 1/3%

12 1/3%

Ans .

13 1/3%

Explanation :
Let amount of the bill = Rs.100
Money deducted =Rs.10
Money received by the holder of the bill = Rs.100-10 = Rs.90
SI on Rs.90 for 10 months = Rs.10
Rate =[(100*10)/(90*10/12)%=13 1/3%

Q.163

If the height of a pole is 2$\sqrt{3}$metres and the length of its shadow is 2 metres,

find the angle of elevation of the sun..

$30^{\circ}$

$45^{\circ}$

$60^{\circ}$

$90^{\circ}$

Ans .

$60^{\circ}$

Explanation :
Let AB be the pole and AC be its shadow.
Let angle of elevation,$\angle$ACB=$\theta$
Then, AB = 2$\sqrt{3}$m AC = 2 m.
Tan $\theta$=AB/AC = $\sqrt[2]{\frac{3}{2}}$=$\sqrt{3}$=>$\theta$
So, the angle of elevation is $60^{\circ}$

Q.164

A ladder leaning against a wall makes an angle of $60^{\circ}$ with the ground. If the

length of the ladder is 19 m, find the distance of the foot of the ladder from the wall.

7.5

9.5

6.5

8.5

Ans .

9.5

Explanation :
Let AB be the wall and BC be the ladder.
Then, $\angle$ACB= $60^{\circ}$ and BC = 19 m.
Let AC = x metres
AC/BC = cos $60^{\circ}$ => x/19 = ½ =>x=19/2 = 9.5
Distance of the foot of the ladder from the wall = 9.5

Q.165

The angle of elevation of the top of a tower at a point on the ground is $30^{\circ}$. On

walking 24 m towards the tower, the angle of elevation becomes $60^{\circ}$. Find the height of the tower.

29 m

22 m

25.6 m

20.76 m

Ans .

20.76 m

Explanation :
Let AB be the tower and C and D be the points of observation. Then,
AB/AD = tan $60^{\circ}$ = $\sqrt{3}$ => AD = AB/$\sqrt{3}$= h/$\sqrt{3}$
AB/AC = tan $30^{\circ}$ = 1/$\sqrt{3}$ AC=AB x$\sqrt{3}$ = h$\sqrt{3}$
CD = (AC-AD) = (h$\sqrt{3}$-h/$\sqrt{3}$)
(h$\sqrt{3}$-h/$\sqrt{3}$) = 24 => h=12$\sqrt{3}$=(12*1.73)=20.76
Hence, the height of the tower is 20.76 m.

Q.166

A man standing on the bank of a river observes that the angle subtended by a

tree on the opposite bank is $60^{\circ}$. When he retires 36 m from the bank, he finds the angle to be $30^{\circ}$.

Find the breadth of the river.

12 m

18 m

15 m

20s m

Ans .

18 m

Explanation :
Let AB be the tree and AC be the river. Let C and D be the two positions of the man. Then,
$\angle$ACB=$60^{\circ}$,$\angle$ADB=$30^{\circ}$ and CD=36 m.
Let AB=h metres and AC=x metres.
Then, AD=(36+x)metres......(1)
AB/AD=tan $30^{\circ}$=1/$\sqrt{3}$ => h/(36+x)=1/$\sqrt{3}$ =>h=(36+x)/$\sqrt{3}$
AB/AC=tan $60^{\circ}$=$\sqrt{3}$ => h/x=$\sqrt{3}$
h=$\sqrt{3}$/x .....(2)
From (i) and (ii), we get:
(36+x)/$\sqrt{3}$x => x=18 m.
So, the breadth of the river = 18 m.

Q.167

A man on the top of a tower, standing on the seashore finds that a boat coming towards him takes 10 minutes for the angle

of depression to change from $30^{\circ}$ to $60^{\circ}$. Find the time taken by the boat to reach the shore from this position.

3 minutes

6 minutes

5 minutes

4 minutes

Ans .

5 minutes

Explanation :
Let AB be the tower and C and D be the two positions of the boat.
Let AB=h, CD=x and AD=y.
h/y=tan $60^{\circ}$ =$\sqrt{3}$ => y=h/$\sqrt{3}$
h/(x+y)=tan $30^{\circ}$=1/$\sqrt{3}$ => x+y=$\sqrt{3}$h
x=(x+y)-y = ($\sqrt{3}$ h-h/$\sqrt{3}$ )=2h/$\sqrt{3}$
Now, 2h/$\sqrt{3}$ is covered in 10 min.
h/$\sqrt{3}$ will be covered in (10*($\sqrt{3}$/2h)*(h/$\sqrt{3}$))=5 min
Hence, required time = 5 minutes.

Q.168

There are two temples, one on each bank of a river, just opposite to each

other. One temple is 54 m high. From the top of this temple, the angles of depression of the top and the foot of the other

temple are $30^{\circ}$ and $60^{\circ}$ respectively. Find the width of the river and the height of the other temple.

18 m

Ans .

18 m

Explanation :
Let AB and CD be the two temples and AC be the river.
Then, AB = 54 m. Let AC = x metres and CD=h metres.
$\angle$ACB=$60^{\circ}$, $\angle$EDB=$30^{\circ}$
AB/AC=tan $60^{\circ}$=$\sqrt{3}$
AC=AB/$\sqrt{3}$=54/$\sqrt{3}$=(54/$\sqrt{3}$*$\sqrt{3}$*$\sqrt{3}$)=18m
DE=AC=18$\sqrt{3}$
BE/DE=tan $30^{\circ}$=1/$\sqrt{3}$
BE=(18$\sqrt{3}$*1/$\sqrt{3}$=18 m
CD=AE=AB-BE=(54-18) m = 36 m.
So, Width of the river = AC = 18$\sqrt{3}$m=18*1.73 m=31.14m
Height of the other temple = CD= 18 m

The following table gives the sales of batteries manufactured by a company

lit the years. Study the table and answer the questions that follow:

YEAR	4AH	7AH	32AH	35AH	55AH	T0TAL
1992	75	144	114	102	108	543
1993	90	126	102	84	426	528
1994	96	114	75	105	135	525
1995	105	90	150	90	75	510
1996	90	75	135	75	90	465
1997	105	60	165	45	120	495
1998	115	85	160	100	145	605

Q.169

The total sales of all the seven years is the maximum for which battery ?

4AH

7AH

32AH

55AH

Ans .

32AH

Explanation :
The total sales (in thousands) of all the seven years for various batteries are:
For 4AH = 75 + 90 + 96 + 105 + 90 + 105 + 115 = 676
For 7AH = 144 + 126 + 114 + 90 + 75 + 60 + 85 = 694
For 32AH = 114 + 102 + 75 + 150 + 135 + 165 + 160 = 901
For 35 AH= 102 + 84 + 105 + 90 + 75 + 45 + 100 = 601
For 55 AH= 108 + 126 + 135 + 75 + 90 + 120 + 145 = 799.
Clearly, sales are maximum in case of 32AH batteries.

Q.170

What is the difference in the number of 35AH batteries sold in 1993 and 1997 ?

24000

28000

35000

39000

Ans .

39000

Explanation :
Required difference = [(84 - 45) x 1000] = 39000

Q.171

The percentage of 4AH batteries sold to the total number of batteries sold

was maximum in the year:

(a) 1994

(b) 1995

(d) 1997

Ans .

1997

Explanation :
The percentages of sales of 4AH batteries to the total sales in different years are:
For 1992 =(75*100/543)%=13.81%
For 1993=(90*100)/528%=17.05%
For 1994=(96*100/465)%=19.35%
For 1995=(105*100/495)%=20.59%
For 1996=(96*100/465)%=19.35%
For 1997=(105*100/495)%=21.21%
For 1998=(115*100/605)%=19.01%
Clearly, the percentage is maximum in 1997.

Q.172

In the case of which battery there was a continuous decrease in sales from 1992 to 1997 ?

(a) 4AH

(b) 7 AH

(d) 35AH

Ans .

35AH

Explanation :
From the table it is clear that the sales of 7AH batteries have
been decreasing continuously from 1992 to 1997.

Q.173

What was the approximate percentage increase in the sales of 55AH

batteries in 1998 compared to that in 1992 ?.

(a) 28%

(b) 31%

(d)34%

Ans .

34%.

Explanation :
Required Percentage =(145-108)/108)*100 %=34.26%=34%.

Study the following table carefully and answer these questions:

NUMBER OF CANDIDATES APPEARED AND QUALIFIED IN A COMPETITIVE

EXAMINATION FROM DIFFERENT STATES OVER THE YEAR

	1997		1998		1999		2000		2001
	App.	Qual.	App.	Qual.	App.	Qual.	App.	Qual.	App.	Qual.
M	5200	720	8500	980	7400	850	6800	775	9500	1125
N	7500	840	9200	1050	8450	920	9200	980	8800	1020
P	6400	780	8800	1020	7800	890	8750	1010	9750	1250
Q	8100	950	9500	1240	8700	980	9700	1200	8950	995
R	7800	870	7600	940	9800	1350	7600	945	7990	885

Q.174

Combining the states P and Q, together in 1998, what is the percentage

of the candidates qualified to that of the canditates appeared?

(a) 10.87%

(b) 11.49%

(d) 12.54%

Ans .

12.35%

Explanation :
Required Percentage=(1020+1240) *100%=(2260*100)/18300%
(8800+9500)=12.35%

Q.175

The percentage of the total number of qualified candidates to the total

number appeared candidates among all the five states in 1999 is :

(a) 11.49%

(b) 11.84%

(d) 12.57

Ans .

11.84%.

Explanation :
Required Percentage= (850+920+890+980+1350) *100% (7400+8450+7800+8700+9800)
=(4990*100)/42150%
=11.84%.

Q.176

What is the percentage of candidates qualified from State N for all the

years together, over the candidates appeared from State N during all the years together?

(a) 12.36%

(b) 12.16%

(d) 11.15%

Ans .

=11.15%

Explanation :

Required Percentage=(84+1050+920+980+1020)/(7500+9200+8450+9200+8800)*100%=(4810*100)/43150*) %
=11.15%

Q.177

What is the average of candidates who appeared from State Q during the

given yeas?

8760

8810

8920

8990

Ans .

8990

Explanation :
Required average =(8100+9500+8700+9700+8950)/5=44950/5=8990

Q.178

In which of the given years the number of candidates appeared from

State P has maximum percentage of qualified candidates?

1998

1999

2000

2001

Ans .

2001

Explanation :
The percentages of candidates qualified to candidates appeared from
State P during different years are:
For 1997= 780 * 100% =12.19% 6400
for 1998 = 1020*100 %=11.59% 8800
For 1999 = 890*100 %=11.41%; 7800
For 2000 = 1010* 100 % = 11.54%. 8 750
For 2001=1250*100 %= 12.82% 9750
Maximum percentage is for the year 2001..

Q.179

Total number of candidates qualified from all the states together in 1997

is approximately what percentage of the total number of candidates qualified from all the states together in 1998 ?

a) 72%

(b) 77%

(d) 83%

Ans .

80%

Explanation :
Required Percentage =( 720 + 840 + 780 + 950 + 870) . x 100
980+1050+1020+1240+940=80%

The following table gives the percentage of marks obtained by seven students in six , different subjects in an examination. Study the table and

answer the questions based on it. The numbers in the brackets give the maximum marks in each subject.

Student	Maths	Chemistry	Physics	Geography	History	Computer Science
Max Marks	(160)	(130)	(120)	(100)	(60)	(40)
Ayush	90	50	90	60	70	80
Aman	100	80	80	40	80	70
sajal	90	60	70	70	90	70
Rohit	80	65	80	80	60	60
Muskan	80	65	85	95	50	90
Tanvi	70	75	65	85	40	60

Q.180

What was the aggregate of marks obtained by Sajal in all the six subjects?

(a)449

(b) 419

(d) 439

Ans .

449

Explanation :
Aggregate marks obtained by Sajal
= [(90% of 150) + (60% of 130) + (70% of 120) + (70% of 100) +(90% of 60) + (70% of 40)] = 135 + 78 + 84 + 70 + 54 + 28 = 449.

Q.181

What is the overall percentage of Thrun?

(a) 52.5%

(b) 55%

(d) 63%

Ans .

60%.

Explanation :
Aggregate marks obtained by Tarun .
= [(65% of 150) + (35% of 130) + (50% of 120) + (77% of 100) + (80% of60) + (80% of 40)] = 97.5 + 45.5 + 60 + 77 + 48 + 32 = 360.
Total maximum marks (of all the six subjects)
= (150 + 130 + 120 + 100 + 60 + 40) = 600.
Overall percentage of Tarun = 360 x 100 % = 60%.

Q.182

What are the average marks obtained by all the seven students in Physics?

(rounded off to two digits after decimal)

(a) 77.26

(b) 89.14

(d) 96.11

Ans .

89.14

Explanation :
Average marks obtained in Physics by all the seven students
= 1/7 [(90% of 120) + (80% of 120) + (70% of 120) + (80% of 120)+ (85% of 120) + (65% of 120) + (50% of 120)]
= 1/7 [(90 + 80 + 70 +80 + 85 + 65 + 50)% of 120]
=1/7 [520% of 120] = 89.14.

Q.183

The number of students who obtained 60% and above marks in all the

subjects is :

(a) 1

(b) 2

(d) None

Ans .

Explanation :
From the table it is clear that Sajal and Rohit have 60% or more
marks in each of the six subjects.

Q.184

In which subject is the overall percentage the best?

(a) History

(b) Maths

(d) Chemistry

Ans .

Maths

Explanation :
We shall find the overall percentage (for all the seven students) with respect to each subject.The overall percentage for any subject is equal to the average of percentages obtained by all the seven students since the maximum marks for any subject is the same for all the students.Therefore, overall percentage for:
(i) Maths = [1/7(90+100+90+80+80+70+65)]%= [1/7(575)]% = 82.14%.
(ii) Chemistry = [1/7(50 + 80 + 60 + 65 + 65 + 75 + 35)]%= [1/7(430)]% = 61.43%. .
(iii) Physics = [1/7(90 + 80 + 70 + 80 + 85 + 65 + 50)]%=[1/7 (520)]% = 74.29%.
(iv) Geography = [1/7(60 + 40 + 70 + 80 + 95 + 85 + 77)]%= [1/7 (507)} = 72.43%.
(v) History = [1/7 (70 + 80 + 90+ 60 + 50 + 40 + 80)]%=1/7 [(470)]% = 67.14%.
(vi) Computer Science = [1/7 (80 + 70 + 70 + 60 + 90 + 60 + 80)]%= [1/7 (510)]% = 72.86%.
Clearly; this. percentage is highest for Maths.

Study the following table carefully and answer tbe questions given below:(Bank P.O. 2001) CLASSIFICATION OF 100 STUDENTS BASED ON THE MARKS OBTAINED BY THEM IN PHYSICS AND CHEMISTRY IN AN EXAMINATION

(Marks out Of 50) Subject	40 and above	30 and above	20 and above	10 and above	0 and above
physics	9	32	80	92	100
chemistry	4	21	66	81	100
(aggregate Average)	7	27	73	87	100

Q.185

The number of students scoring less than 40% marks in aggregate is :

(a) 13

(b) 19

(d) 27

Ans .

Explanation :
We have 40% of 50 =(40/100 x 50)= 20.
Required number = Number of students scoring less than 20 marks in aggregate
= 100 - number of students scoring 20 and above marks in aggregate = 100 - 73 = 27.

Q.186

If at least 60% marks in Physics are required for pursuing higher studies in

Physics,how many students will be eligible to pursue higher studies in Physics?

(a) 27

(b) 32

(d)41

Ans .

Explanation :
We have 60% of 50 =(60 /100x 50) = 30.
Required number = Number of students scoring 30 and above mark in Physics = 32

Q.187

What is the difference between the number of students passed with 30 as

cut-off marks in Chemistry and those passed with :JUas cut-off marks in aggregate?

(a) 3

(b) 4

(d) 6

Ans .

Explanation :
Required difference = (Number of students scoring 30 and
above in mark in Chemistry) (Number of students scoring 30 and above marks in aggregate) = 27 - 21 = 6.

Q.188

The percentage of the number of students getting at least 60% marks in

Chemistry over those getting at least 40% marks in aggregate, is approximately:

(a) 21%

(b) 27%

(d) 31%

Ans .

29%

Explanation :
Number of students getting at least 60% marks in Chemistry
= Number of students getting 30 and above marks in Chemistry = 21.
Number of students getting at least 40% marks in aggregate
= Number of students getting 20 and above marks in aggregate = 73.
Required Percentage = (21/73x 100)% = 28.77% ≈29%.

Q.189

If it is known that at least 23 students were eligible for a Symposium on

Chemistry the minimum qualifying marks in Chemistry for eligibility to Symposium would lie in the range:

(a) 40-50

(b) 30-40

(d) Below 20

Ans .

20-30

Explanation :
Since 66 students get 20 and above marks in Chemistry and out of
these 21 students get 30 and above marks, therefore to select top 35 students in Chemistry, the qualifying marks
should lie in the range 20-30.

The bar graph given below shows the foreign exchange reserves of a country(in million us$)

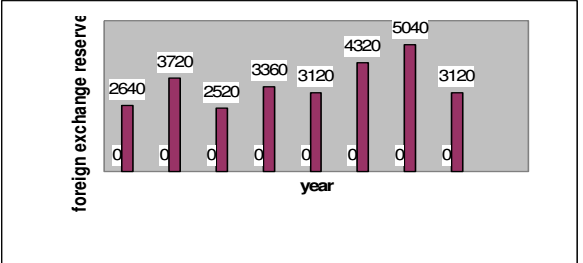
from 1991-92 to 1998-99 .answer the questions basedon this graph. aptitude question of CAT 2008

Q.190

The foreign exchange reserves in 1997-98 was how ,any times that in 1994-95?

(a)0.7

(b) 1.2

(d) 1.5

Ans .

1.5

Explanation :
required ratio = 5040/3360 = 1.5

Q.191

what was the percentage increase in the foreign exchange reserves in 1997-98

over 1993-94?

(a)100

(b)150

(d)620

Ans .

100%

Explanation :
foreign exchange reserve in 1997-98=5040 million us $
foreign exchange reserves in 1993-94=2520 million us$
therefore increase=(5040-2520)=2520 million us $
therefore percentage increase=((2520/2520)*100)%=100%

Q.192

for which year,the percent increase of foreign exchange reserves over the

previous year,is the highest?

(a)1992-93

(b)1993-94

(d)1996-97

Ans .

1992-93

Explanation :
there is an increase in foreign exchange reserves during the years 1992-
93,1994-951996-97,1997-98 as compared to previous year (as shown by bar graph)
the percentage increase in reserves during these years compared to previous year are
(1) for 1992-93 =[(3720-2640)/2640*100]% =40.91%
(2) for 1994-95=[(3360-2520)/2520*100]%=33.33%
(3) for 1996-97=[(4320-3120)/3120*100]%=38.46%
(4) for 1997-98=[(5040-4320)/4320*100]%=16.67%
Clearly, the percentage increase over previous year is highest for 1992-93.

Q.193

the foreign exchange reserves in 1996-97 werw approximately what percent of

the average foreign exchange reserves over the period under review?

(a)95%

(b)110%

(d)125%

Ans .

125%

Explanation :
Average foreign exchange reserves over the given period
= [_x (2640 + 3720 + 2520 + 3360 + 3120 + 4320 + 5040 + 3120) ] million US $
= 3480 million US $.
Foreign exchange reserves in 1996-97 = 4320 million US $. . .
Required Percentage = x 100 % = 124.14% .. 125%. 3480 .

Q.194

the ratio of the number of years,in which the foreign exchange reserves are above the average reserves ,to those in which the reserves are below the average reserves is in Physics?

(a)2:6

(b)3:4

(d)4:4

Ans .

3:5

Explanation :
Average foreign exchange reserves over the given period = 3480 million US $.
The country had reserves above 3480 million US $ during the years 199293,1996-97 and 1997-98 i.e., for 3 years and below 3480 million US $ during the
years 1991-92, 1993-94, 1994-95, 1995-96 and 1998-99 i.e., for 5 years.
Hence, required ratio = 3 : 5.

bar-graph provided on next page gives the sales of books (inthousand numbers) from six branches of a publishing company during two

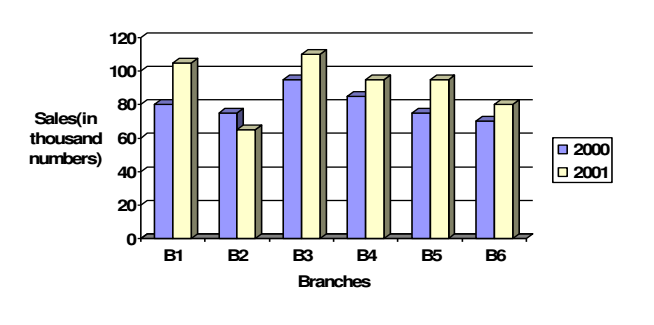
consecutive years 2000 and 2001. Answer the questions based on this bargraph: aptitude question of CAT 2008

Q.195

total sales of branches b1,b3 and b5 together for both the years (in thousandnumbers) is:

(a)250

(b) 310

(d)560

Ans .

560

Explanation :
total sales of branches B1,B3 and B5 for both the years (in thousand
numbers)=(80+105)+(95+110)+(75+95)=560

Q.196

total sales of branch b6 for both the years is what percent of the total sales of branch b3 for both the years?

(a) 68.54%

(b)71.11%

(d)75.55%

Ans .

73.17%

Explanation :
required percentage=[(70+80)/(95+110)*100]%=(150/205*100)%=73.17%

Q.197

what is the average sale of all the branches (in thousand numbers) for the year2000?

(a)73

(b)80

(d)88

Ans .

Explanation :
average sales of all the six branches (in thousand numbers ) for the year 2000=1/6*(80+75+95+85+75+70)=80

Q.198

what is the ratio of the total sales of branch b2 for both years to the total sales of branch b4 for both years ?

3:5

4:5

5:7

7:9

Ans .

7/9

Explanation :
required ratio=(75+65)/(85+95)=140/180=7/9

Q.199

what percent of the average sales of branchesn b1,b2 and b3 in 2001 is the average sales of branches b1,b3 and b6 in 2000?

77.5%

82.5%

85%

87.5%

Ans .

87.5%

Explanation :
average sales(in thousand numbers of branches B1,B3,and B6 in 2000=
1/3*(80+95+70)=245/3
average sales(in thousand numbers of branches B1,B2,and B3 in
2001=1/3*(105+65+110)=280/3
therefore required percentage=[((245/3)/(280/3))*100]%=(245/280*100)%=87.5%

The bar graph provided below gives the data of the production of paper(in thousand tonnes) by three different companies x,y and z over the years .study

the graph and answer the questions that followproduction of paper(in laks tonnes) by three companys x,yand z over the years aptitude question of CAT 2008

Q.200

What is the difference between the production of the company Z in 1998 andcompany y in 1996?

a.2 ,00,000 tons

b.20,00,000 tons

c.20,000 tons

d.2,00,00,000 tons

Ans .

2,00,00,000 tons

Explanation :
required difference =[(45-25)*1,00,000]tons=20,00,000 tons.

Q.201

what is the ratio of the average production of company x in the period 1998 to

2000 to the average production of company y in the same period?

a.1:1

b.15:27

c.23:25

d.27:29

Ans .

Rs. 912

Explanation :
average production of company x in the period 1998-
2000=[1/3*(25+50+40)]=(115/3) lakh tons average production of company y in the period 1998-2000
s[1/3*(35+40+50)]=(125/3) lakh tonstherefore req ratio=(115/3)/(125/3)=115/125=23/25

Q.202

what is the percentage increase in the production of company y from1996 to1999?

a.30%

b.45%

c.50%

d.60%

Ans .

60%c

Explanation :
percentage increase in the production y from 1996-1999=[(40- 25)/25*100]%=(15/25*100)%=60%

Q.203

the avreage production of five years was maximum for which company?

x & y both

x and z both

Ans .

x and z both

Explanation :
average production (in lakh tons)in five years for the three company’s are:
for company x=[1/5*(30+45+25+50+40)]=190/5=38
for company y=[1/5*(25+35+35+40+50)]=185/5=37
for company z=[1/5*(35+40+45+35+35)]=190/5=38
therefore the average production of maximum for both the company’s x and z

Q.204

for which of thw follolwing years the percentage rise / fall in production from previous year is the maximum for company y?

a.1997

b.1998

c.1999

d.2000

Ans .

1997

Explanation :
Percentage change (rise/fall)in the production of Company Y in comparison
to the previous year, for different years are:
For 1997 = [((32-25)/25)*100]% = 40%
For 1998 = [((35-35)/25)*100]% = 0%
For 1999 = [((40-35)/35)*100]% = 14.29%
For 2000 = [((50-40)/40)*100]% = 25%
Hence, the maximum percentage rise/fall in the production of company Y is for 1997.

Q.205

in which year was the percentage of production of company z to the production

of company y the maximum?

a.1996

b.1997

c.1998

d.1999

Ans .

1996

Explanation :
The percentages of production of company z to the production of company
z for various years are:
For 1996 = ((35/25)*100)%=140%; For 1997 = ((40/35)*100)% = 114.29%
For 1998 = ((45/35)*100)%=128.57%; For 1999 = ((35/40)*100)%=87.5%
For 2000 = ((35/50)*100)%=70%
Clearly, this percentage is highest for 1996.

Q.206

In which year,there has been a maximum percentage increase in the amount

invested inRawMaterials as compared to the previous year?

(a)1996

(b) 1997

(d) 1999

Ans .

1996

Explanation :
The percentage increase in the amount invested in raw-materials as
compared to the previous year, for different years are:
For 1996 = [((225-120)/120)*100]% = 87.5%
For 1997 = [((375-225)/225)*100]% = 66.67%
For 1998 = [((525-330)/330)*100]% = 59.09%
For 2000 there is a decrease.

Q.207

Inwhichyear, the percentage change (compared to the previous year) in the

investment onRaw Materials is the same as that in the value of sales of finished goods?

(a)1996

(b) 1997

(d) 1999

Ans .

1997

Explanation :
The percentage change in the amount invested in raw-materials and in the
value of sales of finished goods for different years are:
in year 1996 Percentage change in amount invested in raw-materials[((225-120)/120)*100]% = 87.5%
Percentage change in value of sales of finished goods[((300-200)/200)*100]% = 50%
in year 1997 Percentage change in amount invested in raw-materials[((375-225)/225)*100]% = 66.7%
Percentage change in value of sales of finished goods[((500-300)/300)*100]% = 66.67%
in year 1998 Percentage change in amount invested in raw-materials[((525-330)/330)*100]% = -12%
Percentage change in value of sales of finished goods [((400-500)/500)*100]% = -20%
in year 1999 Percentage change in amount invested in raw-materials[((525-330)/330)*100]% = 59.09%
Percentage change in value of sales of finished goods[((600-400)/400)*100]% = 50%
in year 2000 Percentage change in amount invested in raw-materials[((420-525)/525)*100]% = -20%
Percentage change in value of sales of finished goods [((460-600)/600)*100]% = -23.33%
Thus the percentage difference is same during the year 1997

Q.208

Whatwas the difference between the average amount invested in Raw Materials

during the given period and the average value of sales of finished goods during this period?

(a)Rs. 62.5 lakhs

(b) Rs. 68.5 lakhs

(d)Rs.77.51akhs

Ans .

Rs.77.51akhs

Explanation :
Required difference = Rs. [(1/6)*(200+300+500+400+600+460)- (1/6)*(120+225+375+330+525+420)] lakhs
= Rs. [(2460/6)-(1995/6)] lakhs = Rs.(410-332.5)lakhs = 77.5 lakhs.

Q.209

The value of sales of finished goods in 1999 was approximately what percent of the average amount invested in Raw Materials in the years 1997,1998 and 1999?

(a) 33%

(b) 37%

(d) 49%

Ans .

49%

Explanation :
Required percentage = [(600/(375+300+525))*100]% = 48.78% =>49%

Q.210

The maximum difference between the amount invested in Raw Materials and

the value of sales of finished goods was during the year:

(a) 1995

(b) 1996

(d) 1998

Ans .

1997

Explanation :
The difference between the amount invested in raw-material and the value
of sales of finished goods for various years are :
For 1995 = Rs.(200-120)lakhs = Rs. 80 lakhs
For 1996 = Rs.(200-225)lakhs = Rs. 75 lakhs
For 1997 = Rs. (500-375)lakhs = Rs. 125 lakhs
For 1998 = Rs. (400-330)lakhs = Rs. 70 lakhs.
For 1999 = Rs. (600-525)lakhs = Rs. 75 lakhs
For 2000 = Rs. (460-420)lakhs = Rs. 40 lakhs.
Clearly, maximum difference was during 1997

Directions(questions 211 to 214) : study the following bar-graph and answer the questions given below.

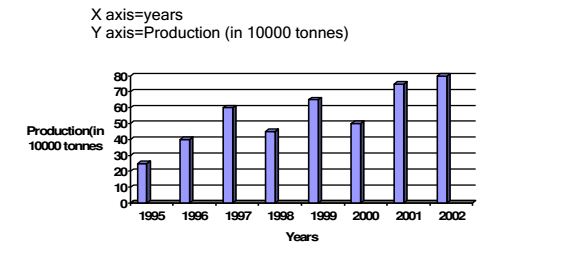
Production of fertilizers by a Company (in 10000 tonnes) over the Years aptitude question of CAT 2008

Q.211

In how many of the given years was the production of fertilizers more than

the average production of the given years?

(a)1

(b)2

(d)5

Ans .

Explanation :
average production of each year=$\frac{25+40+60+45+65+75+80}{8}$=48.75=49

Q.212

The average production of 1996 and 1997 was exactly equal to the

average production of which of the following pairs of years?

(a)2000 and 2001

(b)1999 and 2000

(d)1995 and 1999

Ans .

1995 and 1999

Explanation :
average production of 1996 and 1997=$\frac{40+60}{2}$=50
average of 2000 and 2001=$\frac{50+75}{2}$=62.5
average of 1999 and 2000=$\frac{65+50}{2}$=57.5
average of 1998 and 2000=$\frac{45+50}{2}$=47.5
average of 1995 and 1999=$\frac{25+75}{2}$=50

Q.213

What was the percentage decline in the production of fertilizers from 1997

to 1998?

(a) 331/3%

(b) 30%

(d) 21%

Ans .

25%

Explanation :
increase=60-45=15
%increase=(15/60)*100=25%

Q.214

In which year the percentage increase in production as compared to the

previous year the maximum?

(a) 2002

(b) 2001

(d) 1997

Ans .

2001

Explanation :
the percentage increase in production as compared to the
previous year is maximum in 2001

The following pie-chart shows the sources of funds to be collected by the National

Highways Authority of India (NHAI) for its Phase II projects. Study the pie-chart and answer

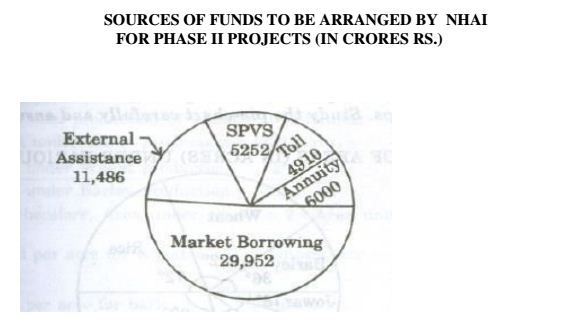
the questions that follow. aptitude question of CAT 2008

Total funds to be arranged for Projects (Phase II) =Rs.57,600 crores.

Q.215

Near about 20% of the funds are to be arranged through:

(a) SPVS

(b) External Assistance

(d) Market Borrowing

Ans .

External Assistance

Explanation :
20% of the total funds to be arranged = Rs.(20% of 57600) crores
= Rs.11520 crores Rs.11486 crores.

Q.216

The central angle corresponding to Market Borrowing is:

(a) 52°

(b) 137.8°

(d) 192.4°

Ans .

($187.2^{\circ}$

Explanation :
Central angle corresponding to Market Borrowing = $[\frac{29952}{57600}*360]^{\circ}$= ($187.2^{\circ}$

Q.217

The approximate ratio of the funds to be arranged through Toll and that through Market Borrowing is:

(a) 2:9

(b) 1:6

(d) 2:5

Ans .

1:6

Explanation :
Required ratio = $\frac{4910}{29952}$= $\frac{1}{6.1}$ =$\frac{1}{6}$

Q.218

If NHAI could receive a total of Rs. 9695 crores as External Assistance, by what percent (approximately) should it increase the Market Borrowings to arrange for the shortage of funds ?

(a) 4.5%

(b) 7.5%

(d) 8%

Ans .

Explanation :
Shortage of funds arranged through External Assistance
=Rs.(11486-9695) crores =Rs. 1791 crores.
therefore, Increase required in Market Borrowings =Rs. 1791 crores.
Percentage increase required = $\frac{1791}{29952}$* 100 % = 5.98 % = 6%

Q.219

If the toll is to be collected through an outsourced agency by allowing a maximum 10%

commission, how much amount should be permitted to be collected by the outsourced agency, so that the project is supported with Rs. 4910 crores ?

(a) Rs.6213 crores

(b) Rs. 5827 crores

(d) Rs. 5216 crores

Ans .

Rs. 5401 crores

Explanation :
Amount permitted = (Funds required from Toll for projects of Phase II ) +(10 % of these funds)
=Rs. 4910 crores + Rs. (10% of 4910) crores
=Rs. (4910 + 491) crores = Rs. 5401 crores.

The pie-chart provided below gives the distribution of land (in a village) under

various food crops. Study the pie-chart carefully and answer the questions that follow.

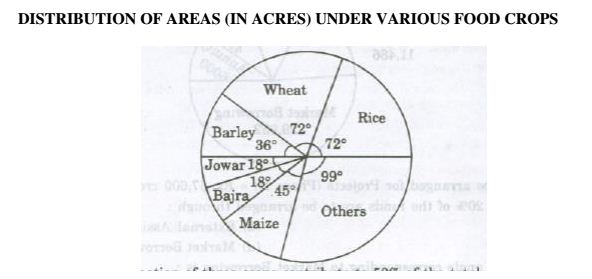
DISTRIBUTION OF AREAS (IN ACRES) UNDER VARIOUS FOOD CROPS aptitude question of CAT 2008

Q.220

Which combination of three crops contribute to 50% of the total area under the food crops ?

(a) Wheat, Barley and Jowar

(b)Rice, Wheat and Jowar

(d)Bajra, Maize and Rice

Ans .

Rice, Wheat and Barley

Explanation :
The total of the central angles corresponding to the three crops which cover 50% of the
total area ,should be 180.Now, the total of the central angles for the given combinations are:
(i) Wheat,Barley and jowar =$72^{\circ}$+ $36^{\circ}$+ $18^{\circ}$ =$126^{\circ}$
(ii) Rice,Wheat and Jowar = $72^{\circ}$+$72^{\circ}$+$18^{\circ}$=$162^{\circ}$
(iii) Rice,Wheat and Barley = $72^{\circ}$+$72^{\circ}$+$36^{\circ}$=$180^{\circ}$
(iv)Bajra,Maize and Rice = $18^{\circ}$+ $45^{\circ}$+$72^{\circ}$ = $135^{\circ}$
Clearly:(iii) is the required combination.

Q.221

If the total area under jowar was 1.5 million acres, then what was the area (in million acres)

under rice?

(a)6

(b)7.5

(d)4.5

Ans .

Explanation :
The area under any of the food crops is proportional to the angle corresponding to that crop.
Let the area under the rice production be x million acres.
Then, 18:72 = 1.5:x =>x=(72*15/18)=6
Thus, the area under rice production be = 6 million acres.

Q.222

If the production of wheat is 6 times that of barley, then what is the ratio between the yield per

acre of wheat and barley ?

(a) 3:2

(b) 3:1

(d) 2:3

Ans .

3:1

Explanation :
Let the total production of barley be T tones and let Z acres of land be put under barley production.
Then, the total production of wheat =(6T) tones.
Also,area under wheat production = (2Z) acres.
$\frac{Area Under Wheat Production}{Area Under Barley Production}$=$\frac{72^{\circ}}{36^{\circ}}$=2
And therefore,Area under wheat = 2*Area under Barley = (2Z)acres
Now, yield per acre for wheat = (6T/2Z) tones/acre = (3T/Z) tones/acre
And yield per acre for barley = (T/Z) tones/acre.
Required ratio = $\frac{3T/Z}{T/Z}$= 3:1.

Q.223

If the yield per acre of rice was 50% more than that of barley, then the production of barley is

what percent of that of rice ?

(a)30%

(b)33 %

(d)36%

Ans .

33%

Explanation :
Let Z acres of land be put under barley production.
$\frac{Area Under Wheat Production}{Area Under Barley Production}$=$\frac{75^{\circ}}{36^{\circ}}$=2
Area under rice production = 2 * area under barley production = (2Z) acres.
Now,if p tones be the yield per acre of barley then ,yield per acre of rice=(p+50% of p) tones =(3/2 p) tones.
Total production of rice = (yield per acre) * (area under production)= (3/2 p)*2Z=(3pZ) tones.
And,Total production of barley = (pz) tones.
Percentage production of barley to that rice = (pZ/3pZ *100)%= 33 1/3%

Q.224

If the total area goes up by 5%, and the area under wheat production goes up by 12% , then

what will be the angle for wheat in the new pie-chart ?

(a)$ 62.4^{\circ}$

(b)$76.8^{\circ}$

(d)$84.2^{\circ}$

Ans .

$76.8^{\circ}$

Explanation :
Initially,let t be the total area under considerations.
The area under wheat production initially was =(72/360 * t)acres = (t/5)acres.
Now,if the total area under consideration be increased by 5%,
then the new value of the total area= (105/100 t) acres.
Also,if the area under wheat production be increased by 12%,
then the new value of area under wheat =|$\frac{t}{5}$ +(12% of $\frac{t}{5}$)| acres = (112t/500)acres.
Central angle corresponding to wheat in the pie-chart
= $[\frac{Area Under Wheat (new)}{Total area (new)}*360]^{\circ}$ = $[\frac{(112t/500)}{(105t/100)}$*360]^{\circ}\) =$76.8^{\circ}$

The following pie-charts show the distribution of students of graduate and post graduate levels in seven different institute-M,N,P,Q,R,S and T in a town.

DISTRIBUTION OF STUDENTS AT GRADUATE AND POST-GRADUATE LEVELS IN SEVEN INSTITUTES-M,N,P,Q,R,S AND T. aptitude question of CAT 2008

Q.225

How many students of institutes M and S are studying at graduate level?

(a) 7516

(b) 8463

(d) 9404

Ans .

(b) 8463

Explanation :
Students of institute M at graduate level = 17% of 27300 = 4641.
Students of institute S at graduate level = 14% of 27300 = 3822
Total number students at graduate level in institutes M and S = 4641+3822=8463.

Q.226

Total number of students studying at post -graduate level from institutes N and P is:

(a) 5601

(b) 5944

(d) 7004

Ans .

Explanation :
Required number = (15% of 24700) + (12% of 24700) = 3705 + 2964 = 6669

Q.227

What is the total number of graduate and post-graduate level students in institute R?

(a) 8320

(b) 7916

(d) 8372

Ans .

(d) 8372

Explanation :
Required number = (18% of 27300) + (14% of 24700) = 4914 + 3458 = 8372.

Q.228

.What is the ratio between the number of students studying at post graduate and graduate levels

respectively from institute S?

(a) 14:19

(b) 19:21

(d) 19:14

Ans .

(d) 19:14

Explanation :
Required ratio =$\frac{21% of 24700}{14% of 27300}$ = $\frac{21 * 24700}{14 * 27300}$ = $\frac{19}{14}$

Q.229

What is the ratio between the number of students studying post graduate level from institute S and the

number of students studying at graduate level from institute Q?

(a) 13:19

(b) 21:13

(d)19:13

Ans .

(d)19:13

Explanation :
Required ratio =$\frac{21% of 24700}{14% of 27300}$ = $\frac{(21 * 24700)}{(13* 27300)}$ = $\frac{19}{13}$

Study the following pie-chart and the table and the answer the questions based on them.

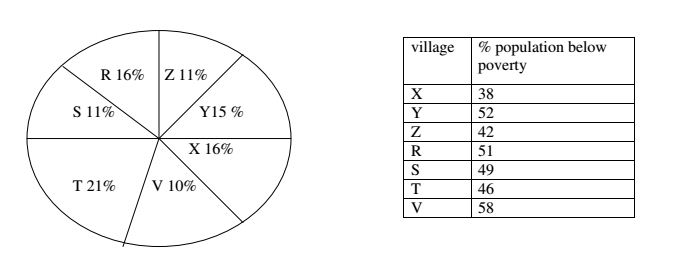
PROPORTION OF POPULATION OF SEVEN VILLAGES IN 1997 aptitude question of CAT 2008

Q.230

Find the population of villages S if the population of village X below poverty line in 1997 is 12160.

(a). 18500

(b) 20500

(d) 26000

Ans .

22000.

Explanation :
Let the population of village X be x
Then,38% of x=12160 => x = $\frac{12160 * 100}{38}$ =3200
Now ,if s be the population village S,then
16:11 = 32000 : s => s= $\frac{11 * 32000}{16}$= 22000.

Q.231

The ratio of the population of the village T below poverty line to that of village Z below poverty line in

1997 is:

(a) 11:23

(b) 13:11

(d) 11:13

Ans .

23:11

Explanation :
Let N be the total population of all the seven villages.
Then ,population of village T below poverty line = 46% of (21% of N) and population of village Z
below poverty line = 42% of (11% of N)
Required ratio =$\frac{46%of 21% of N}{42% of 11% of N}$ = $\frac{46*21}{42*11}$ = $\frac{23}{11}$

Q.232

If the population of village R in 1997 is 32000,then what will be the population of village Y below

poverty line in that year?

(a) 14100

(b)15600

(d) 17000

Ans .

15600

Explanation :
Population of village R = 32000(given)
Let the population of village Y be y.
Then, 16:15 = 32000 : y => y = $\frac{15 * 32000}{16}$= 30000.

Q.233

.If in 1998, the population of villages Y and V increases by 10% each and the percentage of population

below poverty line remains unchanged for all the villages, then find the population of village V below

poverty line in 1998,given that the population of village Y in 1997 was 30000.

(a) 11250

(b) 12760

(d) 13780

Ans .

12760

Explanation :
Population of village Y in 1997 = 30000(given) .
Let the population village V in 1997 be v.
Then, 15:10 = 30000:v => v = $\frac{10 * 30000}{15}$= 20000.
Now population of village V in 1998 = 20000 + (10% 0f 20000) = 20000.
Population of village V below poverty line in 1998 = 58% of 22000 = 12760.

Q.234

If in 1998,the population of village R increases by 10% while that of village Z reduces by 5% compared

that in 1997 and the percentage of population below poverty line remains unchanged for all the

village,then find the approximate ratio of population of village R below poverty line for the year 1999.

(a) 2:1

(b) 3:2

(d) 5:4

Ans .

2:1

Explanation :
Let the total population of all the seven villages in 1997 be N.
Then,population of village R in 1997 = 16% of N = 16/ 100 N
And population of village Z in 1997 = 11% of N =11/100 N
Population of village R in 1999 = {16/100N+(10% of 16/100 N)}=1760/10000 N
and population of village Z in 1999 = {11/100 N-(5% of 11/100 N)} = 1045/10000 N.
Now,population of village R below poverty line for 1999 = 51% of(1760/10000 N)
And population of village Z below poverty line 1999 = 42% of (1045/10000 N)
Required ratio =$\frac{51% of 1760/10000 N}{42% of 1045/10000 N}$ = $\frac{51 * 1760 }{42 * 1045}$ = $\frac{2}{1}$

In a school the periodical examination are held every second month. In a session

during Apr. 2001 – Mar. 2002, a student of Class IX appeared for each of the periodical exams. The aggregate marks

obtained by him in each periodical exam are represented in the line-graph given below. Study the graph and answer

the questions based on it.(S.B.I.P.O 2003)

MARKS OBTAINED BY A STUDENT IN SIX PERIODICAL EXAMS HELD IN EVERY TWO MONTHS DURING THE YEAR IN THE SESSION 2001-02 aptitude question of CAT 2008

Q.235

The total number of marks obtained in Feb. 02 is what percent of the total marks

obtained in Apr. 01?

(a) 110%

(b) 112.5%

(d) 116.5%

Ans .

112.5%

Explanation :
Required percentage = [(405/360)*100] % = 112.5 %

Q.236

What are the average marks obtained by the student in all the periodical exams of

during the session.

(a) 373

(b) 379

(d) 385

Ans .

381

Explanation :
Average marks obtained in all the periodical exams.
= (1/6)*[360+370+385+400+404] = 380.83 = 381.

Q.237

what is the percentage of marks obtained by the student in the periodical exams of

Aug. 01 and Oct. 01 taken together?

(a) 73.25%

(b) 75.5%

(d) 78.75%

Ans .

78.75%

Explanation :
Required percentage = [(370+385)/(500+500) * 100] % = [(755/1000)*100]% =75.5%

Q.238

In which periodical exams there is a fall in percentage of marks as compared to the

previous periodical exams?

(a) None

(b) Jun. 01

(d) Feb. 01

Ans .

none

Explanation :
As is clear from graph, the total marks obtained in periodical exams, go on increasing.
Since, the maximum marks for all the periodical exams are same , it implies that the percentage of marks also goes on increasing. Thus,
in none of the periodical exams, there is a fall in percentage of marks compared to the previous exam.

Q.239

In which periodical exams did the student obtain the highest percentage increase in

marks over the previous periodical exams?

(a) Jun. 01

(b) Aug. 01

(d) Dec. 01

Ans .

Oct. 01

Explanation :
Percentage increases in marks in various periodical exams compared to the previous exams are:
For Jun. 01 = [(365-360)/360 * 100 ] % = 1.39 %
For Aug. 01 = [(370-365)/365 * 100 ] % = 1.37 %
For Oct. 01 = [(385-370)/370 * 100 ] % = 4.05%
For Dec. 01 = [(400-385)/385 * 100 ] % = 3.90 %
For Feb. 02 = [(405-400)/400 * 100 ] % = 1.25 %

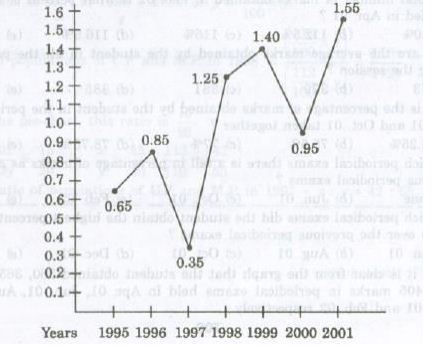
The following line- graph the ratio of the amounts of imports by a Company to the amount of exports from that Company over the period from 1995 to 2001. The questions given below are based on this graph. (S.B.I.P.O 2001)Ratio of value of Import to Export by a Company over the Years aptitude question of CAT 2008

Q.240

In how many of the given years were the exports more than the imports?

a. 1

b. 2

c. 3

d. 4

Ans .

Explanation :
The exports are more than the imports implies that the ratio of value of imports to exports is less than 1.
Now, this ratio is less than 1 in the years 1995,1996,1997 and 2000. Thus, there are four such years.

Q.241

The imports were minimum proportionate to the exports of the Company in the year:

a..1995

b.1996

c.1997

d.2001

Ans .

1997

Explanation :
The imports are minimum proportionate to the exports implies that the ratio of the
value of imports to exports has the minimum value.
Now, this ratio has a minimum value of 0.35 in 1997, i.e., the imports are minimum proportionate to the exports in 1997.

Q.242

If the imports of the Company in 1996 was Rs.272 crores, the exports from the

Company in 1996 was:

a. Rs.370 crores

b.Rs.320 crores

c.Rs.280 crores

d.Rs.275 crores

Ans .

b.Rs.320 crores

Explanation :
Ratio of imports to exports in the years 1996=0.85.
Let the exports in 1996=Rs.320 crores.
Then,272/x =0.85 implies x=272/.85 = 320..

Q.243

What was the percentage increase in imports from 1997 to 1998?

a. 72

b.56

c.28

d.Data inadequate

Ans .

Data inadequate

Explanation :
The graph gives only the ratio of imports to exports for different
years. To find the percentage increase in imports from 1997 to 1998, we require more details such as the
value of imports or exports during these years. Hence, the data is inadequate to answer this question.

Q.244

If the imports in 1998 was Rs.250 crores and the total exports in the years 1998 and 1999 together was Rs.500 crores, then the imports in 1999 was:

a.Rs.250 crores

b.Rs.300 crores

c.Rs 357 crores

d.Rs 420 crores

Ans .

d.Rs 420 crores

Explanation :
The ratio of imports to exports for the years 1998 and 1999 are 1.25 and 1.40 respectively.
Let the exports in the year 1998 = Rs. x crores
Then, the exports in the year 1999=Rs(500-x) crores.
1.25=250/x implies x=250/1.25=200
Thus the exports in the year 1999=Rs. (500-200)crores=Rs.300 crores
Let the imports in the year 1999=Rs. y crores
Then, 1.4=y/300 implies y=(300*1.4)=420.
Imports in the year 1999=Rs.420 crores..

Study the following line-graph and answer the question based on it.Number of vehicle Manufactured by Two Companies over the Years

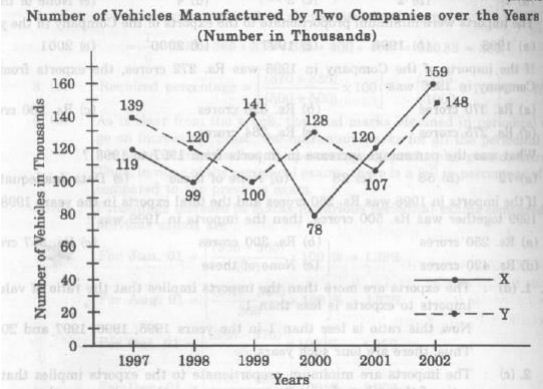
(Numbers in thousands) aptitude question of CAT 2008

Q.245

What is the difference between the total productions of the two Companies in the given years?

a. 19000

b. 22000

c.26000

d.28000

Ans .

26000

Explanation :
Total production of Company X from 1997 to 2002
= 119000+99000+141000+78000+120000+159000 = 716000
and total production of Company Y from 1997 to 2002
=139000+120000+100000+128000+107000+148000=742000
Difference=742000-716000=26000.

Q.246

What is the difference between the numbers of vehicles manufactured by Company Y in

2000 and 2001?

a.50000

b.42000

c.33000

d.21000

Ans .

21000

Explanation :
Require difference = 128000-107000 = 21000.

Q.247

What is the average number of vehicles manufactured by Company X over the given

period? (rounded off to the nearest integer)

a.119333

b.113666

c.112778

d.111223

Ans .

119333

Explanation :
Average number of vehicles manufactured by Company X
= (91/6)* (119000 + 99000 + 141000 + 78000 + 120000 + 159000) = 119333.

Q.248

In which of the following years, the difference between the productions of Companies X

and Y was the maximum among the given years?

a.1997

b.1998

c.1999

d.2000

Ans .

2000

Explanation :
The difference between the production of Companies X and Y in various years are.
For 1997 = (139000 – 119000) = 20000;
For 1998 = (120000 – 99000) = 21000;
For 1999 = (141000 – 100000) = 41000;
For 2000 = (128000 – 78000) = 50000;
For 2001 = (120000 – 107000) = 13000;
For 2003 = (159000 – 148000) = 11000;
Clearly, maximum difference was in 2000

Q.249

The production of Company Y in 2000 was approximately what percent of the production

of Company X in the same year?

a.173.

b.164

c.132

d.97

Ans .

164

Explanation :
Required percentage = [( 128000/78000)* 100] % = 164 %.

The following line-graph gives the percent profit earned by two Companies X and Y

during the period 1996 – 2001. Study the line – graph and answer the questions that are based on on it.

Percentage Profit Earned by Two Companies X and Y over the Given years % profit/ loss = [(Income – Expenditure) / Expenditure] * 100 aptitude question of CAT 2008

Q.300

If the expenditure of Company Y in 1997 was Rs. 220 crores, what was its income in 1997?

(a). Rs. 312 crores

(b). Rs. 297 crores

(d) Rs. 275 crores

Ans .

(b). Rs. 297 crores

Explanation :
Profit percent ofcompany Y in 1997=35.
Let the income of company Y in 1997 be Rs.x crores
Then,35 = $\frac{x-220}{220}$ X 100 =>x =297
Income of company Yin 1997 = Rs.297crores.

Q.301

If the incomes of the two companies were equal in 1999,then what was the ratio of

expenditure of Company X to that of company Y in 1999 ?

(a) 6:5

(b) 5:6

(d) 16:15

Ans .

16:15

Explanation :
Let the incomes of the twocompanies X and Yin 1999 be Rs.x and let the
Expenditures of companies X and Y in 1999 be E1 and E2 respectively
Then, for Company X we have:
50= $\frac{x-E1}{E1}$ x 100 => $\frac{50}{100}$ = $\frac{x}{E1}$ -1 => x = $\frac{150}{100}$ E1
Also, for the Company Y we have:
60 = $\frac{x-E2}{E2}$ *100 =>$\frac{60}{100}$ = $\frac{x}{E2}$ -1 =>x = $\frac{160}{100}$ E2
From (i) and (ii),we get
$\frac{150}{100}$ E1=$\frac{160}{100}$ E2 => $\frac{E1}{E2}$ = $\frac{160}{150}$= $\frac{16}{15}$(Required ratio).

Q.302

The incomes of the companies X and Y in 2000 were in the ratio of 3:4

respectively.What was the respective ratio of their expenditures in 2000?

(a) 7:22

(b) 14:19

(d)27:35

Ans .

15:22

Explanation :
Let the incomes in 2000 of companies X and Y be 3x and 4x respectively.And let
the expenditure in 2000 of companies X and Y be E1 and E2 respectively.
Then, for company X we have:
65= $\frac{3x-E1}{E1}$ x 100 => $\frac{65}{100}$ = $\frac{3x}{E1}$-1 =>E1=3x *$\frac{100}{165}$
For company Y we have:
50 = $\frac{4x-E2}{E2}$ *100 => $\frac{50}{100}$ = $\frac{4x}{E2}$-1 =>E2 = 4x* $\frac{100}{150}$
From (i)and(ii) we get:
$\frac{E1}{E2}$ = $\frac{3x*(100/165)}{4x*(100/150)}$ =$\frac{3* 150}{4*165}$ =$\frac{15}{22}$ (Required ratio)

Q.303

If the expenditure ofcompanies X and Y in 1996 were equal and the total income of the

two companies in 1996 was Rs.342 crores, what was the total profit of the twocompanies together in 1996 ? (Profit = Income – Expenditure)

(a) Rs.240crores

(b) Rs.171crores

(d) Rs.102crores

Ans .

Rs.102crores

Explanation :
Let the expenditures of each of the Companies X and Y in 1996 be
Rs.xcrores.And let the income of Company X in 1996 be Rs.zcrores so that the income of Company Y in 1996 =Rs.(342-z)crores.
Then,for company X we have:
40= $\frac{z-x}{x}$ *100 => $\frac{40}{100}$ =$\frac{ z}{x}$ -1 => x = $\frac{100z}{140}$
Also for company Y we have:
45= $\frac{(342-z)-x}{x}$ *100 => $\frac{45}{100}$= $\frac{ (342-z)}{x}$ -1 =>x = $\frac{(342 –z)}{145}$* 100
From(i)and (ii) we get:
$\frac{100z}{140}$ = $\frac{(342-z)*100}{145}$ =>z = 168
Substituting z=168 in (i),we get: x=120
Total expenditure of companies X and Y in 1996=2x=Rs.240crores.
Total income of companies X and Y in 1996=Rs.342 crores.
Total profit =Rs.(342-240)crores =Rs.102 crores

Q.304

The expenditure ofcompany X in the year 1998 was Rs.200 crores and the income

Company X in 1998 was the same as its expenditure in 2001 was:

(a) Rs.465crores

(b)Rs.385crores

(c)Rs.295crores

(d)Rs.255crores

Ans .

Rs.465crores

Explanation :
Let the income of company X in 1998 be Rs.x crores.
Then,55= $\frac{x-200}{200}$ *100 => x = 310.
Expenditure of Company X in 2001= Income of company X in 1998 = Rs.310crores
Let the income of company X in 2001 be Rs.z crores
Then,50 = $\frac{z-310}{310}$ *100 =>z = 465.
Income of company X in 2001 = Rs.465 crores.

upscfever.com

Journey of a Thousand Miles begins with One Click!!!

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments