TYPE-I

Q.1

A train is travelling at the rate of 45km/hr. How many seconds it will take to cover a distance of \( \frac{4}{5}\)

(1) 36 sec.

(2) 64 sec.

(3) 90 sec.

(4) 120 sec.

Ans .

(2) 64 sec.

Explanation :

Time taken=\( \frac{Distance}{Time}
= \frac{ \frac{4}{5}}{45} hour
=\frac{4*60*60}{5*45} sec.
= 64sec.\)

Q.2

An aeroplane covers a certain distance at a speed of 240 km hour in 5 hours. To cover the same distance in 1\( \frac{2}{3} \) hours, it must travel at a speed of :

1) 300 km./hr.

(2) 360 km./hr.

(3) 600 km./hr.

(4) 720 km./hr.

Ans .

(4) 720 km./hr.

Explanation :

Let the required speed is x km/ hr Then, \(240 * 5=\frac{5}{3}*x .., x = 720 km/hr\)

Q.3

A man walking at the rate of 5 km/hr. crosses a bridge in 15 minutes. The length of the bridge (in metres) is :

(1) 600

(2) 750

(3) 1000

(4) 1250

Ans .

(4) 1250

Explanation :

Speed of the man =\( 5km/hr =5 * \frac{1000}{60} m / min =\frac{250}{3} m / min.\) Time taken to cross the bridge = 15 minutes Length of the bridge = speed × time = \( \frac{250}{3}*15m= 1250m.\)

Q.4

A man crosses a road 250 metres wide in 75 seconds. His speed in km/hr is :

(1) 10

(2) 12

(3) 12.5

(4) 15

Ans .

(2) 12

Explanation :

Speed = \( \frac{Distance}{Time} = \frac{250}{75}= \frac{10}{3}\) m/sec= \( \frac{10}{3}\) * \( \frac{18}{5} \)km/hr ..,1 m/s = \( \frac{18}{5}\) km / hr = 2 × 6 km/hr. = 12 km/hr.

Q.5

An athlete runs 200 metres race in 24 seconds. His speed (in km/ hr) is :

(1) 20

(2) 24

(3) 28.5

(4) 30

Ans .

(4) 30

Explanation :

Speed =\( \frac{Distance}{Time}\)= \( \frac{200}{24}\)m/s. =\( \frac{200}{24}\) * \( \frac{18}{5}\) = 30 km/h

Q.6

A car goes 10 metres in a sec- ond. Find its speed in km/hour.

(1) 40

(2) 32

(3) 48

(4) 36

Ans .

(4) 36

Explanation :

Speed of car = 10 m/sec. Required speed in kmph =\( \frac{10*18}{5}\)= 36 km/hr.

Q.7

A car travelling at a speed of 40 km/hour can complete a journey in 9 hours. How long will it take to travel the same distance at 60 km/hour ?

(1) 6 hours

(2) 3 hours

(3) 4 hours

(4) 4\( \frac{1}{2}\) hours

Ans .

(1) 6 hours

Explanation :

= Speed × Time = 40 × 9 = 360 km. The required time at 60 kmph= \( \frac{360}{60}\)=6hours.

Q.8

A man travelled a certain dis- tance by train at the rate of 25 kmph. and walked back at the rate of 4 kmph. If the whole journey took 5 hours 48 min- utes, the distance was

(1) 25 km

(2) 30 km

(3) 20 km

(4) 15 km

Ans .

(3) 20 km

Explanation :

Total time = 5 hours 48 minutes=5 + \( \frac{48}{60}\)={5+ \( \frac{4}{5}\) }hours.=\( \frac{29}{5}hours\)..,\( \frac{x}{25}\) + \( \frac{x}{4}\)=\( \frac{29}{5}\)
\( \frac{4x+25x}{100}\)=\( \frac{29}{5}\)
5 × 29x = 29 × 100
x=\( \frac{29*100}{5*29}\)= 20 km.

Q.9

A boy goes to his school from his house at a speed of 3 km/hr and returns at a speed of 2 km/ hr. If he takes 5 hours in going and coming, the distance be- tween his house and school is :

(1) 6 km

(2) 5 km

(3) 5.5 km

(4) 6.5 km

Ans .

(1) 6 km

Explanation :

Let the required distance be x km. Then,\( \frac{x}{3}\) + \( \frac{x}{2}\) =5
\( \frac{2x+3x}{6}\)=5
5x = 6 × 5
=6km.

Q.10

A boy runs 20 km in 2.5 hours. How long will he take to run 32 km at do uble the previous speed ?

(1) 2 hours

(2) 6 hours

(3) 9 hours

(4) 1 hours.

Ans .

(1) 2 hours

Explanation :

The boy covers 20 km in 2.5 hours. Speed=\( \frac{20}{2.5}\)= 8 km/hr..
New speed = 16 km/hr
..,Time=\( \frac{32}{16}\)=2hours.

Q.11

A train is moving with the speed of 180 km/hr. Its speed (in metres per second) is :

(1) 5

(2) 40

(3) 30

(4) 50

Ans .

(4) 50

Explanation :

Speed = 180 kmph
=\( \frac{180*5}{18}\)m/sec = 50 m/sec
..,1 km / hr =\( \frac{5}{18}\)m/s.

Q.12

A man riding his bicycle covers 150 metres in 25 seconds. What is his speed in km per hour ?

(1) 25

(2) 21.6

(3) 23

(4) 20.

Ans .

(2) 21.6

Explanation :

Speed=\( \frac{150}{25}\)= 6 m/sec
= 6 *\( \frac{18}{5}\)=21.6 kmph

Q.13

A and B travel the same distance at speed of 9 km/hr and 10 km/ hr respectively. If A takes 36 minutes more than B, the dis- tance travelled by each is

(1) 48 km

(2) 54 km

(3) 60 km

(4) 66 km

Ans .

(2) 54 km

Explanation :

Let the distance between A and B be x km, then \( \frac{x}{9}\)-\( \frac{x}{10}\)=\( \frac{36}{60}\)=\( \frac{3}{5}\)
\( \frac{x}{90}\)=\( \frac{3}{5}\)
x =\( \frac{3}{5}\)*90 = 54 km.

Q.14

A person started his journey in the morning. At 11 a.m. he covered \( \frac{3}{8}\)of the journey and on the same day at 4.30 p.m. he covered \( \frac{5}{6}\)of the journey. He started his journey at

(1) 6.00 a.m.

(2) 3.30 a.m.

(3) 7.00 a.m.

(4) 6.30 a.m

Ans .

(4) 6.30 a.m

Explanation :

Difference of time
= 4.30 p.m – 11.a.m. =5*\( \frac{1}{2}\)hours=\( \frac{11}{2}\)hours
\( \frac{5}{6}\)-\( \frac{3}{8}\)=\( \frac{20-9}{24}\)=\( \frac{11}{24}\)part
\( \frac{11}{24}\)part of the journey is covered in \( \frac{11}{2}\)hours
\( \frac{3}{8}\)part of the journey is covered in
\( \frac{11}{2}\) * \( \frac{24}{11}\)* \( \frac{3}{8}\)=\( \frac{9}{2}\)hours
4*\( \frac{1}{2}\)hours.
Clearly the person started at 6.30a.m.

Q.15

The speed of a bus is 72 km/hr. The distance covered by the bus in 5 seconds is

(1) 100 m

(2) 60 m

(3) 50 m

(4) 74.5 m

Ans .

(1) 100 m

Explanation :

Speed of bus = 72 kmph
=\( \frac{75*5}{18}\)metre/second
= 20 metre/second
Required distance= 20 × 5 = 100 metre

Q.16

Two men start together to walk a certain d istance, one at 4 km/h and another at 3 km/h. The former arrives half an hour before the latter. Find the dis- tance.

(1) 8 km

(2) 7 km

(3) 6 km

(4) 9 km

Ans .

(3) 6 km

Explanation :

If the required distance be x km, then \( \frac{x}{3}\)-\( \frac{x}{4}\)=\( \frac{1}{2}\)
\( \frac{4x-3x}{12}\)=\( \frac{1}{2}\)
\( \frac{x}{12}\)=\( \frac{1}{2}\)=x = 6 km

Q.17

A train starts from a place A at 6 a.m. and arrives at another place B at 4.30 p.m. on the same day. If the speed of the train is 40 km per hour, find the distance trav- elled by the train ?

(1) 420 km

(2) 230 km

(3) 320 km

(4) 400 km

Ans .

(1) 420 km

Explanation :

Time=10*\( \frac{1}{2}\)hours
\( \frac{21}{2}\)hours
Speed = 40 kmph
Distance = Speed × Time
40*\( \frac{21}{2}\)= 420 km

Q.18

Walking at the rate of 4 km an hour, a man covers a certain dis- tance in 3 hours 45 minutes. If he covers the same distance on cycle, cycling at the rate of 16·5 km/hour, the time taken by him is

(1) 55.45 minutes

(2) 54.55 minutes

(3) 55.44 minutes

(4) 45.55 minutes

Ans .

(2) 54.55 minutes

Explanation :

Distance covered on foot 4*3\( \frac{3}{4}\)km=15km.
Time taken on cycle
\(\frac{Distance}{Speed}\)=\( \frac{15}{16.5}\)hour
\(\frac{15*60}{16.5}\)minutes
= 54.55 minutes

Q.19

A train covers a distance of 10 km in 12 minutes. If its speed is decreased by 5 km/hr, the time taken by it to cover the same dis- tance will be :

(1) 10 minutes

(2) 13 minutes 20 sec

(3) 13 minutes

(4) 11 minutes 20 sec

Ans .

(2) 13 minutes 20 sec

Explanation :

Speed of Train=\( \frac{Distance}{Time}\)
\( \frac{10}{\frac{12}{60}}\)kmph
\( \frac{10*60}{12}\)=50kmph
New speed = 45 kmph
Required time =\( \frac{10}{45}\)hour
=\( \frac{2}{9}*60 minutes\)
=\( \frac{40}{3}\)minutes
= 13 minutes 20 seconds

Q.20

A man walks ‘a’ km in ‘b’ hours. The time taken to walk 200 me- tres is

(1)\( \frac{200b}{a}\)hours

(2)\( \frac{b}{5a}\)hours

(3)\( \frac{b}{a}\)hours

(4)\( \frac{ab}{200}\)hours

Ans .

(2)\( \frac{b}{5a}\)hours

Explanation :

Man's speed=\( \frac{Distance}{Time}\)
\( \frac{a}{b}\)kmph
\( \frac{1000a}{b}\)m/hour
Time taken in walking 200metre =\( \frac{200}{\frac{1000a}{b}}\)=\( \frac{b}{5a}\)hours

Q.21

The speed 3 \( \frac{1}{3}\)m/sec when expressed in km/hour becomes

(1) 8

(2) 9

(3) 10

(4) 12

Ans .

(4) 12

Explanation :

1 m/sec = \( \frac{18}{5}\)kmph ..,\( \frac{10}{3}\)m/sec
\( \frac{18}{5}\)*\( \frac{10}{3}\)=12kmph

Q.22

A bullock cart has to cover a dis- tance of 120 km. in 15 hours. If it covers half of the journey in\( \frac{3}{5}\)th time, the speed to cover the remaining distance in the time left has to be

(1) 6.4 km/hr

(2) 6.67 km/hr

(3) 10 km/hr

(4) 15 km/hr

Ans .

(3) 10 km/hr

Explanation :

Remaining Time
=\( \frac{2}{5}\)*15=6 hours
Remaining Speed
=\( \frac{60}{6}\)=10kmph

Q.23

A train covers a certain distance in 210 minutes at a speed of 60 kmph. The time taken by the train, to cover the same distance at a speed of 80 kmph is :

(1) 3\( \frac{5}{8}\)hours.

(2) 2\( \frac{5}{8}\)hours.

(3) 4\( \frac{5}{8}\)hours.

(4) 3 hours.

Ans .

(2) 2\( \frac{5}{8}\)hours.

Explanation :

Speed of train = 60 kmph
Time = 210 minutes
\( \frac{210}{60}\)hours or \( \frac{7}{2}\)hours
Distance covered
=60*\( \frac{7}{2}\)=210km
Time taken at 80 kmph
=\( \frac{210}{80}\)=\( \frac{21}{8}\)hours
=2\( \frac{5}{8}\)hours

Q.24

A man rides at the rate of 18 km/ hr, but stops for 6 mins. to change horses at the end of ev- ery 7th km. The time that he will take to cover a distance of 90 km is

(1) 6 hrs.

(2) 6 hrs. 12 min.

(3) 6 hrs. 18 min.

(4) 6 hrs. 24 min.

Ans .

(2) 6 hrs. 12 min.

Explanation :

90 km = 12 × 7km + 6 km. To cover 7 km total time taken =\( \frac{7}{18}\)hours+6 min.=\( \frac{88}{3}\)min.So,(12 × 7 km) would be covered in 12* \( \frac{88}{3}\) min. and remaining 6 km. is \( \frac{6}{18}\)hrs or 20 min.
Total time=\( \frac{1056}{3}\)+20
=\( \frac{1116}{3*60}\)hours=6*\( \frac{1}{5}\)hours
= 6 hours 12 minutes.

Q.25

A speed of 30.6 km/.hr is the same as

(1) 8.5 m/sec.

(2) l0 m/sec.

(3) 12 m/sec.

(4) 15.5 m/sec.

Ans .

(1) 8.5 m/sec.

Explanation :

30.6 kmph
= (30.6*\( \frac{5}{18}\) )m/sec. = 8.5 m/sec

Q.26

A man covers \( \frac{2}{15}\)of th total journey by train,\( \frac{9}{20}\) by bus and the remaining 10 km on foot. His total journey (in km) is

(1) 15.6

(2) 24

(3) 16.4

(4) 12.8

Ans .

(2) 24

Explanation :

Let the total journey be of x km, then \( \frac{2x}{15}\)+\( \frac{9x}{20}\)+10=x
x-\( \frac{2x}{15}\)-\( \frac{9x}{20}\)=10
\( \frac{60x-8x-27x}{60}\)=10
\( \frac{25x}{60}\)=10
x=\( \frac{60*10}{25}\)=24km.

Q.27

You arrive at your school 5 min- utes late if you walk with a speed of 4 km/h, but you arrive 10 minutes before the scheduled time if you walk with a speed of 5 km/h. The distance of your school from your house (in km) is

(1) 4

(2) 5

(3) 10

(4) 2

Ans .

(2) 5

Explanation :

If the required distance be = x km, then\( \frac{x}{4}\)-\( \frac{x}{5}\)=\( \frac{10+5}{60}\)
\( \frac{5x-4x}{20}\)=\( \frac{1}{4}\)
\( \frac{x}{20}\)=\( \frac{1}{4}\)
x=\( \frac{1}{4}\)*20=5km

Q.28

Sarita and Julie start walking from the same place in the oppo- site directions. If Julie walks at a speed of 2\( \frac{1}{2}\)km/hr and Sarita at a speed of 2 km/hr, in how much time will they be 18 km apart ?

(1) 4.0 hrs.

(2) 4.5 hrs

(3) 5.0 hrs

(4) 4.8 hrs

Ans .

(1) 4.0 hrs.

Explanation :

Relative speed
{\( \frac{5}{2}\)+2}kmph=\( \frac{9}{2}\)kmph
Time=\( \frac{Distance}{Relative speed}\)=\( \frac{18}{ \frac{9}{2}}\)
\( \frac{18*2}{9}\)=4hours

Q.29

A man travelled a distance of 80 km in 7 hrs partly on foot at the rate of 8 km per hour and partly on bicycle at 16km per hour. The distance travelled on the foot is

(1) 32 km

(2) 48 km

(3) 36 km

(4) 44 km

Ans .

(1) 32 km

Explanation :

Journey on foot = x km
Journey on cycle = (80 – x) km
\( \frac{x}{8}\)+\( \frac{80-x}{16}\)=7
\( \frac{2x+80-x}{16}\)=7
x + 80 = 16 × 7 = 112
x = 112 - 80 = 32 km.

Q.30

A car driver leaves Bangalore at 8.30 A.M. and expects to reach a place 300 km from Bangalore at 12.30 P.M. At 10.30 he finds that he has covered only 40% of the distance. By how much he has to increase the speed of the car in order to keep up his sched- ule?

(1) 45 km/hr

(2) 40 km/hr

(3) 35 km/hr

(4) 30 km/hr

Ans .

(4) 30 km/hr

Explanation :

Distance covered by car in 2 hours=\( \frac{300*40}{100}\)=120 km
Remaining distance
= 300 – 120 = 180 km
Remaining time = 4 – 2
= 2 hours
Required speed=\( \frac{180}{2}\)=90kmph
Original speed of car =\( \frac{120}{2}\)=60kmph
Required increase in speed
= 90 – 60 = 30 kmph

Q.31

A man is walking at a speed of 10 kmph. After every km, he takes a rest for 5 minutes. How much time will he take to cover a distance of 5 km?

(1) 60 minutes

(2) 50 minutes

(3) 40 minutes

(4) 70 minutes

Ans .

(2) 50 minutes

Explanation :

Time taken in covering 5 Km =\( \frac{5}{10}\)=\( \frac{1}{2}\)hour = 30 minutes That person will take rest for four times.Required time= (30 + 4 × 5) minutes= 50 minutes

Q.32

A train covers a distance of 10 km in 12 minutes. If its speed is decreased by 5 km/hr, the time taken by it to cover the same dis- tance is equal to

(1) 40 minutes

(2) \( \frac{40}{3}\)minutes

(3) 20 minutes

(4) 15 minutes

Ans .

(2) \( \frac{40}{3}\)minutes

Explanation :

Time = 12 minutes
= \( \frac{12}{60}\)hours=\( \frac{1}{5}\)hours
=Speed of train=\( \frac{10}{\frac{1}{5}}\)=50kmph
New speed = 50 – 5 = 45 kmph
Required time=\( \frac{Distance}{Speed}\)
=\( \frac{10}{45}\)=\( \frac{2}{9}\)hours
\( \frac{2}{9}\)*60minutes
=\( \frac{40}{3}\)minutes.

Q.33

Motor-cyclist P started his jour- ney at a speed of 30 km/hr. Af- ter 30 minutes, motor-cyclist Q started from the same place but with a speed of 40 km/hr. How much time (in hours) will Q take to overtake P ?

(1) 1

(2) \( \frac{3}{2}\)

(3) \( \frac{3}{8}\)

(4) 2

Ans .

(2) \( \frac{3}{2}\)

Explanation :

Distance covered by motor cyclist P in 30 minutes =30*\( \frac{1}{2}\)=15km Relative speed = 40 – 30 = 10 kmph \ Required speed = Time taken to cover is km at 10 kmph =\( \frac{15}{10}\)=\( \frac{3}{2}\)hours.

Q.34

A is twice as fast as B and B is thrice as fast as C is. The jour- ney covered by C in 1\( \frac{1}{2}\)hours will be covered by A in

(1) 36 sec.

(2) 15 minutes

(3) 30 minutes

(4) 1 hour

Ans .

(2) 64 sec.

Explanation :

Speed of B = x kmph (let) Speed of A = 2x kmph Speed of C =\( \frac{x}{3}\)kmph \( \frac{Speed of A }{Speed of C}\)=\( \frac{2x}{\frac{x}{3}}\)=6 Required time =\( \frac{1}{6}\)of\( \frac{3}{2}\) \( \frac{1}{4}\)hour = 15 minutes

Q.35

A truck travels at 90 km/hr for the first 1\( \frac{1}{2}\)hours.After that ittravels at 70 km/hr. Find the time taken by the truck to travel 310 kilometres.

(1) 2.5 hrs

(2) 3 hrs

(3) 3.5 hrs

(4) 4 hrs

Ans .

(4) 4 hrs

Explanation :

Distance covered by truck in \( \frac{3}{2}\)hours
= Speed × Time
=90*\( \frac{3}{2}\)=135km.
Remaining distance
= 310 – 135 = 175 km
Time taken at 70 kmph
\( \frac{175}{70}\)=2.5hours
Total time = 1.5 + 2.5
= 4 hours

Q.36

A car travels at a speed of 60 km/ hr and covers a particular dis- tance in one hour. How long will it take for another car to cover the same distance at 40 km/hr ?

(1) \( \frac{5}{2}\)hours

(2) 2 hours

(3) \( \frac{3}{2}\)hours

(4) 1 hour

Ans .

(3) \( \frac{3}{2}\)hours

Explanation :

Distance = Speed × Time
= 60 km.
Time taken at 40 kmph
=\( \frac{60}{40}\)=\( \frac{3}{2}\)hours

Q.37

A student goes to school at the \( \frac{5}{2}\)km/hr and reaches 6 minutes late. If he travels at the speed of 3 km/hr, he reaches 10 minutes earlier. The distance of the school is

(1) 45 km

(2) 20 km

(3) 10 km

(4) 4 km

Ans .

(4) 4 km

Explanation :

Distance of school = x km
Difference of time
= 16 minutes =\( \frac{16}{60}\)hours
\( \frac{x}{\frac{5}{2}}\)-\( \frac{x}{3}\)=\( \frac{16}{60}\)
=\( \frac{2x}{5}\)-\( \frac{x}{3}\)=\( \frac{4}{15}\)
=\( \frac{6x-5x}{15}\)=\( \frac{4}{15}\)
=\( \frac{x}{15}\)=\( \frac{4}{15}\)
x=\( \frac{4}{15}\)*15=4km.

Q.38

Sriya with her family travelled from Bolpur to Suri by car at a speed of 40 km/hr and returned to Bolpur at a speed of 50 km/ hr. The average speed for the whole journey is

(1) 44\( \frac{4}{9}\)km/hr.

(2) 45 km/hr

(3) 45\( \frac{1}{2}\)km/hr

(4) 44.78 km/hr

Ans .

(1) 44\( \frac{4}{9}\)km/hr.

Explanation :

Average speed of journey
={\ \frac{2xy}{x+y}\)kmph
=\( \frac{2*40*50}{40+50}\)=\( \frac{2*40*50}{90}\)
\( \frac{400}{9}\)=44\( \frac{4}{9}\)kmph.

Q.39

A journey takes 4 hours 30 min- utes at a speed of 60 km/hr. If the speed is 15 m/s, then the journey will take

(1) 5 hours

(2) 5 hours 30 minutes

(3) 6 hours

(4) 6 hours 15 minutes

Ans .

(1) 5 hours

Explanation :

60 kmph =\( \frac{60*5}{18}\)m/sec
\( \frac{50}{3}\)m/sec.
Speed=\( \frac{1}{Time}\)
S 1 × T 1 = S 2 × T 2
\( \frac{50}{3}\)*\( \frac{9}{2}\)= 15 × T 2
75 = 15 × T 2
t2= \( \frac{75}{15}\)=5hours.

Q.40

The distance between 2 places R and S is 42 km. Anita starts from R with a uniform speed of 4 km/ h towards S and at the same time Romita starts from S towards R also with some uniform speed. They meet each other after 6 hours. The speed of Romita is

(1) 18 km/hour

(2) 3 kmph

(3) 20 km/hour

(4) 8 km/hour

Ans .

(2) 3 kmph

Explanation :

Speed of Romita = x kmph
(let) Distance = Speed × Time
According to the question,
4 × 6 + x × 6 = 42
Þ 6x = 42 – 24 = 18
Þ x = 18 ÷ 6 = 3 kmph

Q.41

A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot at the rate 4 kmph and partly on bicycle at the rate 9 kmph. The distance travelled on foot is

(1) 16 km

(2) 14 km

(3) 17 km

(4) 15 km

Ans .

(1) 16 km

Explanation :

Distance travelled by farmer
on foot = x km (let)
\ Distance covered by cycling
= (61–x ) km.
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{4}\)+\( \frac{61-x}{9}\)=9
\( \frac{9x + 61 * ́ 4 – 4x}{9*4}\)=9
5x + 244 = 9 × 9 × 4 = 324
5x = 324 – 244 = 80
x=\( \frac{80}{5}\)= 16 km.

Q.42

A bus moving at 40 km per hour covers a distance in 6 hours 15 minutes. If it travels the same distance at 50 km per hour how long will it take to cover the dis- tance ?

(1) 2 hrs.

(2) 6 hrs.

(3) 4 hrs.

(4) 5 hrs.

Ans .

(4) 5 hrs.

Explanation :

Distance = Speed × TIme
[40*6\( \frac{1}{4}\)]km
[\( \frac{40*25}{4}\)]km = 250 km
New speed = 50 kmph
Required time
\( \frac{Distance}{Speed}\)=\( \frac{250}{50}\)=5 hours

Q.43

A student starting from his house walks at a speed of 2 \( \frac{1}{2}\)km/hour and reaches his school 6 minutes late. Next day starting at the same time he increases his speed by 1 km/hour and reach- es 6 minutes early. The distance between the school and his house is

(1) 4km.

(2) \( \frac{1}{2}\)km

(3) 6 km

(4)\( \frac{7}{4}\)km

Ans .

(4) \( \frac{7}{4}\)km

Explanation :

Distance between school and
house = x km (let)
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{\frac{5}{2}}\)-\( \frac{x}{\frac{7}{2}}\)=\( \frac{6+6}{60}\)=\( \frac{1}{5}\)
(Difference of time = 6 + 6 =12 minutes
\( \frac{2x}{5}\)-\( \frac{2x}{7}\)=\( \frac{1}{5}\)
\( \frac{14x-10x}{35}\)=\( \frac{2x}{5}\)
\( \frac{4x}{35}\)=\( \frac{1}{5}\)
4x=\( \frac{35}{5}\)=7
x=\( \frac{7}{4}\)km.

Q.44

A man starts from a place P and reaches the place Q in 7 hours He travels \( \frac{1}{4}\)th of the distance at 10 km/hour and the remain- ing distance at 12 km/hour. The distance between P and Q is

(1) 72 km

(2) 90 km

(3) 80 km

(4) 33 km

Ans .

(3) 80 km

Explanation :

Let the total distance be 4x km.
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{10}\)+\( \frac{3x}{12}\)=7
\( \frac{x}{10}\)+\( \frac{x}{4}\)=7
\( \frac{2x+5x}{20}\)=7
7x = 7 × 20
x=\( \frac{7*20}{7}\)= 20 km.
PQ = 4x = 4 × 20 = 80 km.

Q.45

A student goes to school at the rate of 2\( \frac{1}{2}\)km/hr and reaches 6 minutes late. If he travels at the speed of 3 km/hr. he is 10 min- utes early. What is the distance to the school?

(1) 4 km

(2) 6 km

(3) 9 km

(4) 1 km

Ans .

(1) 4 km

Explanation :

Let the distance of school be x km.
Difference of time = 6 + 10
= 16 minutes=\( \frac{16}{60}\)hour
\( \frac{4}{15}\)hour
Time=\( \frac{Distance}{Speed}\)
\( \frac{x}{\frac{5}{2}}\)-\( \frac{x}{3}\)=\( \frac{4}{15}\)
\( \frac{6x-5x}{15}\)=\( \frac{4}{15}\)
x = 4 km.

Q.46

A man travels for 5 hours 15 min- utes. If he covers the first half of the journey at 60 km/h and rest at 45 km/h. Find the total dis- tance travelled by him.

(1) 36 sec.

(2) 189 km.

(3) 378 km.

(4) 270 km.

Ans .

(4) 270 km.

Explanation :

Let the distance covered be 2x km.
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{60}\)+\( \frac{x}{45}\)=5\( \frac{15}{60}\)=5\( \frac{1}{4}\)
5\( \frac{3x+4x}{180}\)=5\( \frac{21}{4}\)
7x=\( \frac{21}{4}\)*180
x=\( \frac{21*180}{4*7}\)=135km
Length of total journey
= 2 × 135 = 270 km.

Q.47

A car can finish a certain journey in 10 hours at the speed of 42 kmph. In order to cover the same distance in 7 hours, the speed of the car (km/h) must be increased by :

(1) 12

(2) 15

(3) 18

(4) 24.

Ans .

(3) 18

Explanation :

Distance covered by car
= 42 × 10 = 420 km.
New time = 7 hours
Required speed\( \frac{420}{7}\)
= 60 kmph.
Required increase
= (60 – 42) kmph
= 18 kmph

Q.48

A man cycles at the speed of 8km/hr and reaches office at 11 am and when he cycles at the speed of 12 km/hr he reaches office at 9 am. At what speed should he cycle so that he reach- es his office at 10 am?

(1) 9.6 kmph.

(2) 10 kmph.

(3) 11.2 kmph.

(4) Cannot be determined

Ans .

(1) 9.6 kmph.

Explanation :

Distance of the office= x km.Difference of time = 2 hours
\( \frac{x}{8}\)-\( \frac{x}{12}\)=2
\( \frac{3x-2x}{24}\)=2
\( \frac{x}{24}\)=2
x = 48 km.
Time taken at the speed of 8kmph=\( \frac{48}{8}\)= 6 hours
Required time to reach the office at 10 a.m. i.e., in 5 hours
=\( \frac{48}{5}\)kmph
= 9.6 kmph

Q.49

A bus travels at the speed of 36 km/hr, then the distance covered by it in one second is

(1) 10 metre.

(2) 15 metre

(3) 12.5 metre

(4) 13.5 metre

Ans .

(1) 10 metre.

Explanation :

Speed of bus = 36 kmph.
36*\( \frac{5}{18}\)m/sec.
= 10 m/sec.
\ Distance covered in 1 second
= 10 metre

Q.50

Two buses travel to a place at 45 km./hr. and 60 km./hr. respec- tively. If the second bus takes 5 \( \frac{1}{2}\)hours less than the first for the journey, the length of the jour- ney is :

(1) 900 km.

(2) 945 km.

(3) 990 km.

(4) 1350 km.

Ans .

(3) 990 km.

Explanation :

Time taken by bus moving at
60 kmph = t hours
Distance = Speed × Time
60*t=45*(t+\( \frac{11}{2}\)
60t – 45t =\( \frac{45*11}{2}\)
15t=\( \frac{45*11}{2}\)
t=\( \frac{45*11}{15*2}\)=\( \frac{33}{2}\)hours
Required distance
\( \frac{60*33}{2}\)= 990 km

Q.51

A train is running at a speed of 116 km/hr. The distance covered by the train in metres in 18 sec- onds is :

(1) 900 metre

(2) 1160 metre

(3) 508 metre

(4) 580 metre

Ans .

(4) 580 metre

Explanation :

Speed of train = 116 kmph
116*\( \frac{5}{18}\)m./sec.
\( \frac{580}{18}\)m./sec.
Required distance
= Speed × Time
\( \frac{580}{18}\)*18metre
= 580 metre

Q.52

A man travels \( \frac{3}{4}\) th of the distance of his journey by bus, \( \frac{1}{6}\)th by rickshaw and 2 km on foot. The total distance travelled by the man is :

(1) 12 km

(2) 18 km

(3) 20 km.

(4) 24 km.

Ans .

(4) 24 km.

Explanation :

Part of journey covered by bus
and rickshaw,\( \frac{3}{4}\)+\( \frac{1}{6}\)=\( \frac{9+2}{12}\)=\( \frac{11}{12}\)
Distance covered on foot
=1-\( \frac{11}{12}\)=\( \frac{1}{12}\)part
Total journey
= 12 × 2 = 24 km.

Q.53

To cover a certain distance with a speed of 60 km/hr, a train takes 15 hours. If it covers the same distance in 12 hours, what will be its speed?

(1) 65 km/h

(2) 70 km/h

(3) 75 km/h

(4) 80 km/h

Ans .

(3) 75 km/h

Explanation :

Distance covered by train in
15 hours = Speed × Time
= (60 × 15) km. = 900 km.
Required speed to cover 900 km.
in 12 hours =\( \frac{900}{12}\)= 75 kmph

Q.54

Sound travels at 330 metre per second. The distance (in kilome- tre) of a thunder cloud when its sound follows the flash after 10 seconds is :

(1) 0.33 km.

(2) 3.3 km.

(3) 33 km.

(4) 33.3 km.

Ans .

(2) 3.3 km.

Explanation :

Distance = Speed × Time = 330 × 10 = 3300 metre \( \frac{3300}{1000}\) km. = 3.3 km.

Q.55

A man travels some distance at a speed of 12 km/hr and returns at a speed of 9 km/hr. If the to- tal time taken by him is 2 hrs 20 minutes the distance is

(1) 35 km..

(2) 21 km.

(3) 9 km.

(4) 12 km.

Ans .

(4) 12 km.

Explanation :

Let the required distance be x km.
Time = 2 hours 20 minutes
=2\( \frac{1}{3}\)hours
According to the question,
\( \frac{x}{12}\)+\( \frac{x}{9}\)=\( \frac{7}{3}\)
\( \frac{7x}{36}\)=\( \frac{7}{3}\)
x=\( \frac{7}{3}\)*\( \frac{36}{7}\)= 12 km.

TYPE-2

Q.1

The length of a train and that of a platform are equal. If with a speed of 90 km/hr the train crosses the pl atform in o ne minute, then the length of the train (in metres) is :

(1) 500

(2) 600

(3) 750

(4) 900

Ans .

(3) 750

Explanation :

Let the length of train be x metre Speed = 90 km/hr
\( \frac{90*5}{18}\)metre / sec. = 25 metre/sec.
Distance covered in 60 sec. = 25 × 60 = 1500 metres
Now, according to question, 2x = 1500
x = 750 metre

Q.2

A train passes two bridges of lengths 800 m and 400 m in 100 seconds and 60 seconds respectively. The length of the train is :

(1) 80 m

(2) 90 m

(3) 200 m

(4) 150 m

Ans .

(3) 200 m

Explanation :

When a train crosses a bridge it covers the distance equal to length of Bridge & its own length Let the length of the train be = x Speed of the train \( \frac{x + 800}{100}\)m/s
Since train passes the 800 m bridge in 100 seconds. Again, train passes the 400 m bridge in 60 seconds.
\( \frac{400 + x}{\frac{x + 800}{100}}\)= 60
\( \frac{(400+x)*100}{x+800}\)=60
40000 + 100x
= 60x + 48000
100x – 60x = 48000 – 40000
40x = 8000
x= \( \frac{8000}{40}\)= 200 m

Q.3

A train 300 metres long is run- ning at a speed of 25 metres per second. It will cross a bridge of 200 metres in

(1) 5 seconds

(2) 10 seconds

(3) 20 seconds

(4) 25 seconds

Ans .

(3) 20 seconds

Explanation :

In crossing the bridge, the train travels its own length plus the length of the bridge. Total distance (length)
= 300 + 200 = 500 m.
Speed = 25m/sec.
The required time
= 500 ÷ 25 = 20 seconds

Q.4

A train 800 metres long is run- ning at the speed of 78 km/hr. If it crosses a tunnel in 1 minute, then the length of the tunnel (in metres) is :

(1) 77200

(2) 500

(3) 1300

(4) 900

Ans .

(2) 500

Explanation :

When a train crosses a tun- nel, it covers a distance equal to the sum of its own length and tunnel.
Let the length of tunnel be x Speed = 78 kmph
\( \frac{78*1000}{60*60}\)m/sec. =\( \frac{65}{3}\)m/sec.
Speed=\( \frac{Distance}{Time}\)
\( \frac{65}{3}\)=\( \frac{800+x}{60}\)
(800 + x ) × 3 = 65× 60
800 + x = 65 × 20 m
x = 1300 – 800 = 500
Length of tunnel = 500 metres.

Q.5

A train is moving at a speed of 132 km/hour. If the length of the train is 110 metres, how long will it take to cross a railway platform 165 metres long?

(1) 5 seconds

(2) 7.5 seconds

(3) 10 seconds

(4) 15 seconds

Ans .

(2) 7.5 seconds

Explanation :

When a train crosses a rail- way platform, it travels a distance equal to sum of length of platform and its own length. Speed = 132 kmph =132*\( \frac{5}{18}\)=\( \frac{110}{3}\)m/sec. Required time \( \frac{110+165}{\frac{110}{3}}\)sec. =\( \frac{275*3}{110}\)= 7 . 5 seconds

Q.6

A train takes 18 seconds to pass through a platform 162 m long and 15 seconds to pass through another platform 120 m long. The length of the train (in m) is :

(1) 70

(2) 80

(3) 90

(4) 105

Ans .

(3) 90

Explanation :

Let the length of the train be x metres.
When a train corsses a platform it covers a distance equal to the sum of lengths of train and plat- form. Also, the speed of train is same.
\( \frac{x+162}{18}\)=\( \frac{x+120}{15}\)
6x + 720 = 5x + 810
6x – 5x = 810 – 720
x = 90
\ The length of the train = 90m

Q.7

A train, 150 m long, takes 30 seconds to cross a bridge 500 m long. How much time will the train take to cross a platform 370 m long ?

(1) 36 secs

(2) 30 secs

(3) 24 secs

(4) 18 secs

Ans .

(3) 24 secs

Explanation :

When a train croses a bridge, distance covered = length of (bridge + train).
Speed of train
=\( \frac{150+500}{30}\)
\( \frac{650}{30}\)=\( \frac{65}{3}\)m/sec.
Time taken to cross the 370m long platform
=\( \frac{370 + 150}{\frac{65}{3}}\)
=\( \frac{520*3}{65}\)= 24 seconds

Q.8

A 120 metre long train is running at a speed of 90 km per hour. It will cross a railway platform 230 m long in :

(1) 5 seconds

(2)2 seconds

(3)7 seconds

(4)14 seconds

Ans .

(4)14 seconds

Explanation :

Speed of train = 90 kmph
90*\( \frac{5}{18}\)= 25 m/sec
Distance covered = 230 + 120 = 350 m
Time taken=\( \frac{350}{25}\)
= 14 seconds

Q.9

A train travelling at a speed of 30 m/sec crosses a platform, 600 metres long, in 30 seconds. The length (in metres) of train is

(1) 120

(2) 150

(3) 200

(4) 300

Ans .

(4) 300

Explanation :

Let the length of train be x According to the question,
\( \frac{x+600}{30}\)=30
x + 600 = 900
x = 900 – 600 = 300 m

Q.10

A train with a uniform speed passes a platform, 122 metres long, in 17 seconds and a bridge, 210 metres long, in 25 seconds. The speed of the train is

(1) 46.5 km/hour

(2) 37.5 km/hour

(3) 37.6 km/hour

(4) 39.6 km/hour

Ans .

(4) 39.6 km/hour

Explanation :

Let the length of the train be x According to the question,
\( \frac{x+122}{17}\)=\( \frac{x+210}{25}\)
25x + 3050 = 17x + 3570
25x – 17x = 3570 – 3050
8x = 520
x=\( \frac{520}{8}\)= 65 metres
Speed of the train =\( \frac{65+122}{17}\)
\( \frac{187}{17}\)metre/second
= 11 metre/second
\( \frac{11*18}{5}\)kmph
= 39.6 kmph

Q.11

A train, with a uniform speed, crosses a platform, 162 metres long, in 18 seconds and another platform, 120 metres long, in 15 seconds. The speed of the train is

(1) 14 km/hr

(2) 42 km/hr

(3) 50.4 km/hr

(4) 67.2 km/hr

Ans .

(3) 50.4 km/hr

Explanation :

Let the Length of the train be x
Then, \( \frac{x+162}{6}\)=\( \frac{x+120}{5}\)
6x + 720 = 5x + 810
x = 810 – 720 = 90
Speed of the train \( \frac{90+162}{18}\)m/sec
\( \frac{252}{18}\)*\( \frac{18}{5}\)kmph
= 50.4 kmph

Q.12

A train travelling with uniform speed crosses two bridges of lengths 300 m and 240 m in 21 seconds and 18 seconds respec- tively. The speed of the train is :

(1) 72 km/hr

(2) 68 km/hr

(3) 65 km/hr

(4) 60 km/hr

Ans .

(1) 72 km/hr

Explanation :

Let the length of the train be x Speed of train
\( \frac{x+300}{21}\)=\( \frac{x+240}{18}\)
\( \frac{x+300}{7}\)=\( \frac{x + 240}{6}\)
7x + 1680 = 6x + 1800
x = 120
Speed of train \( \frac{x+300}{21}\)=\( \frac{420}{21}\)= 20 m/sec
\( \frac{20*18}{5}\)kmph = 72 kmph

Q.13

A train, 110m long , is running at a speed of 60km/hr. How many seconds does it take to cross another train, 170 m long, standing on parallel track ?

(1) 15.6 sec

(2) 16.8 sec

(3) 17.2 sec

(4) 18 sec

Ans .

(2) 16.8 sec

Explanation :

Speed of Train,
=\( \frac{Sum of length of both trains}{Time taken}\)
\( \frac{60*5}{18}\)=\( \frac{110+170}{t}\)=\( \frac{280}{t}\)
t=\( \frac{280*18}{60*5}\)= 16.8 seconds.

Q.14

A train of length 500 feet crosses a platform of length 700 feet in 10 seconds. The speed of the train is

(1) 70 ft/second

(2) 85 ft/second

(3) 100 ft/second

(4) 120 ft/second

Ans .

(4) 120 ft/second

Explanation :

Speed of Train,
\( \frac{Length of ( train + platform )}{Time taken to cross}\)
\( \frac{500+700}{10}\)feet/second
= 120 feet/second

Q.15

A train 200 m long running at 36 kmph takes 55 seconds to cross a bridge. The length of the bridge is

(1) 375 m.

(2) 300 m.

(3) 350 m.

(4) 325 m.

Ans .

(3) 350 m.

Explanation :

Speed of train = 36kmph
=36*\( \frac{5}{18}\)= 10 m/sec.
If the length of bridge be x me- tre, then
10=\( \frac{200+x}{55}\)
200 + x = 550
x = 550 – 200 = 350 metre.

Q.16

A train 270 metres long is run- ning at a speed of 36 km per hour, then it will cross a bridge of length 180 metres in :

(1) 40 sec

(2) 45 sec

(3) 50 sec

(4) 35 sec

Ans .

(2) 45 sec

Explanation :

36 kmph ={36*\( \frac{5}{18}\)}m/sec
= 10 m/sec.
Required time=\( \frac{270+180}{10}\)= 45 seconds

Q.17

A train 50 metres long passes a platform of length 100 metres in 10 seconds. The speed of the train in metre/second is

(1) 50

(2) 10

(3) 15

(4) 20

Ans .

(3) 15

Explanation :

Speed of train
=\( \frac{Length of (train + platform)}{Time taken in crossing}\)
=\( \frac{50+100}{10}\)
=\( \frac{150}{10}\)=15m/sec

Q.18

A train 50 metre long passes a platform 100 metre long in 10 sec- onds. The speed of the train in km/hr is

(1) 10

(2) 54

(3) 15

(4) 100

Ans .

(2) 54

Explanation :

Speed of train
\( \frac{Length of platform and train}{Time taken in crossing}\)
=\( \frac{100+50}{10}\)metre/second
= 15 metre/second
15*\( \frac{18}{5}\)kmph
= 54 kmph

Q.19

How many seconds will a train 120 metre long running at the rate of 36 km/hr take to cross a bridge of 360 metres in length ?

(1) 48 sec

(2) 40 sec

(3) 46 sec

(4) 36 sec

Ans .

(1) 48 sec

Explanation :

Speed of train = 36 kmph
{\( \frac{36*5}{18}\)m/sec.
=10 m/sec.
Required time
=\( \frac{Length of train and bridge}{Speed of train}\)
=\( \frac{120+360}{10}\)=\( \frac{480}{10}\)
= 48 seconds

Q.20

If a man running at 15 kmph crosses a bridge in 5 minutes, the length of the bridge is

(1) 1000 metres

(2) 500 metres

(3) 750 metres

(4) 1250 metres

Ans .

(4) 1250 metres

Explanation :

Time = 5 minutes
=\( \frac{1}{12}\)hour
Length of bridge = Speed × Time
=15*\( \frac{1}{12}\)=(\ \frac{5}{4}\)km
=\( \frac{5}{4}\)*1000metre
= 1250 metre

Q.21

A 200 metre long train is running at a speed of 72 km/hr. How long will it take to cross 800metre long bridge ?

(1) 50 seconds

(2) 40 seconds

(3) 60 seconds

(4) 30 seconds

Ans .

(1) 50 seconds

Explanation :

Speed of train = 72 kmph
=\( \frac{72*5}{18}\)m/sec.
= 20 m/sec.
Required time
\( \frac{Length of train and bridge}{Speed of train}\)
=\( \frac{200+800}{20}\)
=\( \frac{1000}{20}\)=50 sec.

Q.22

A train passes two bridges of lengths 500 m and 250 m in 100 seconds and 60 seconds respec- tively. The length of the train is :

(1) 152 m

(2) 125 m

(3) 250 m

(4) 120 m

Ans .

(2) 125 m

Explanation :

Length of train = x metre (let)
Speed of train
=\( \frac{Length of train and bridge}{Time taken in crossing}\)
\( \frac{x+500}{100}\)=\( \frac{x+250}{60}\)
\( \frac{x+500}{5}\)=\( \frac{x+250}{3}\)
5x + 1250 = 3x + 1500
5x – 3x = 1500 – 1250
2x = 250
x=125metre

Q.23

A train 150 metre long takes 20 seconds to cross a platform 450 metre long. The speed of the train in, km per hour, is :

(1) 750

(2) 100

(3) 106

(4) 104

Ans .

(3) 750

Explanation :

Q.24

A moving train passes a platform 50 metre long in 14 seconds and a lamp post in 10 seconds. The speed of the train (in km/h) is :

(1) 24

(2) 36

(3) 40

(4) 45

Ans .

(4) 45

Explanation :

Let the length of train be x metre.
When a train crosses a platform, distance covered by it = length of train and platform. Speed of Train,
=\( \frac{x+50}{14}\)=\( \frac{x}{10}\)
=\( \frac{x+50}{7}\)=\( \frac{x}{5}\)
7x = 5x + 250
7x – 5x = 250
2x = 250 Þ x =\( \frac{250}{2}\)
= 125 metre
Speed of Train=\( \frac{x}{10}\)
\( \frac{125}{10}\)m./sec.
\( \frac{125}{10}\)*\( \frac{18}{5}\)kmph
=45 kmph

Q.25

The lengths of a train and that of a platform are equal. If with a speed of 90 km/hr the train crosses the pl atform in o ne minute, then the length of the train (in metres) is (3) 750 (4) 900

(1) 500

(2) 600

(3) 750

(4) 900

Ans .

(3) 750

Explanation :

Let, length of train = length
of platform = x metre
Speed of train = 90 kmph
\( \frac{90*5}{18}\)m/sec.
= 25 m/sec.
Speed of train
=\( \frac{Length of train and platform}{Time taken in crossing}\)
25=\( \frac{2x}{60}\)=2x = 25 × 60
x=\( \frac{25*60}{2}\)= 750 metre

Q.26

A train, 500 metre long, running at a uniform speed, passes a sta- tion in 35 seconds. If the length of the platform is 221 metre, the speed of the train in km/hr is

(1) 73.11

(2) 74.16

(3) 24.76

(4) 78.54

Ans .

(2) 74.16

Explanation :

Speed of train,
\( \frac{Length of train and platform}{Time taken in crossing}\)
=\( \frac{221+500}{35}\)m/sec
=\( \frac{721}{35}\)m/sec
=\( \frac{721*18}{35*5}\)kmph
= 74.16 kmph

Q.27

A train, 200 metre long, is run- ning at a speed of 54 km/hr. The time in seconds that will be taken by train to cross a 175 metre long bridge is :

(1) 12.5

(2) 20

(3) 25

(4) 10

Ans .

(3) 25

Explanation :

Speed of train = 54 kmph
\( \frac{54*5}{18}\)m/sec
= 15 m/sec.
Required time
\( \frac{Length of train and bridge}{Speed of train}\)
\( \frac{200+175}{15}\)sec
\( \frac{375}{15}\)sec
= 25 seconds

TYPE-3

Q.1

A train 180 m long moving at the speed of 20 m/sec. over-takes a man moving at a speed of 10m/ sec in the same direction. The train passes the man in :

(1) 6 sec

(2) 9 sec

(3) 18 sec

(4) 27 sec

Ans .

(3) 18 sec

Explanation :

Relative speed of man and train
= 20 – 10 = 10m/sec.
Required time =\( \frac{180}{10}\)
= 18 seconds

Q.2

A train 100m long is running at the speed of 30 km/hr. The time (in second) in which it will pass a man standing near the railway line is :

(1) 10

(2) 11

(3) 12

(4) 15

Ans .

(3) 12

Explanation :

In this situation, the train covers it length.
Required time
\( \frac{100}{30*1000}\)hr
\( \frac{100 *60 * 60}{30*1000}\)= 12 seconds

Q.3

How many seconds will a 500 metre long train take to cross a man walking with a speed of 3 km/hr. in the direction of the mov- ing train if the speed of the train is 63 km/hr ?

(1) 25 sec

(2) 30 sec

(3) 40 sec

(4) 45 sec

Ans .

(3) 30 sec

Explanation :

Relative speed of train = 63–3 = 60 kmph
60*\( \frac{5}{18}\)m/sec
Time=\( \frac{Length of train}{Relative speed}\)
=\( \frac{500*18}{60*5}\)=30sec.

Q.4

A train is 125 m long. If the train takes 30 seconds to cross a tree by the railway line, then the speed of the train is :

(1) 14 km/hr

(2) 15 km/hr

(3) 16 km/hr

(4) 12 km/hr

Ans .

(2) 15 km/hr

Explanation :

Speed=\( \frac{Distance}{time}\)
\( \frac{125}{30}\)= 4 . 16 m / s
= 4 . 16 m / s = 4.16*\( \frac{18}{5}\)
= 15 km/hr

Q.5

A 120 m long train takes 10 sec- onds to cross a man standing on a platform. What is the speed of the train ?

(1) 12 m/sec.

(2) 10 m/sec.

(3) 15 m/sec.

(4) 20 m/sec.

Ans .

(1) 12 m/sec.

Explanation :

In crossing a man standing on platform, train crosses its own length.
Speed of train \( \frac{120}{10}\)= 12 m/s

Q.6

A 75 metre long train is moving at 20 kmph. It will cross a man standing on the platform in

(1) 12 seconds

(2) 14 seconds

(3) 12.5 seconds

(4) 13.5 seconds

Ans .

(4) 13.5 seconds

Explanation :

Speed of train (in m/s)
20*\( \frac{5}{18}\)=\( \frac{50}{9}\)m/sec
Required time=\( \frac{75}{50}\)*9
= 13.5 seconds

Q.7

In what time will a train 100 metres long cross an electric pole, if its speed be 144 km/hour ?

(1) 2.5 seconds

(1) 5 seconds

(3) 3 sec

(4) 2.7 sec

Ans .

(1) 2.5 seconds

Explanation :

Speed of the train
= 144 kmph =144*\( \frac{5}{18}\)
= 40 m/s
When a train crosses a pole, it covers a distance equal to its own length.
The required time =\( \frac{100}{40}\)=\( \frac{5}{2}\)= 2 . 5 seconds.

Q.8

A man observed that a train 120 m long crossed him in 9 seconds. The speed (in km/hr) of the train was

(1) 42

(2) 45

(3) 48

(4) 55

Ans .

(3) 48

Explanation :

Speed of train =\( \frac{120}{9}\)*\( \frac{18}{5}\)= 48 kmph

Q.9

If a train, with a speed of 60 km/ hr, crosses a pole in 30 seconds, the length of the train (in metres) is :

(1) 1000

(2) 900

(3) 750

(4) 500

Ans .

(4) 500

Explanation :

Speed of train = 60 kmph =60*\( \frac{5}{18}\)=\( \frac{50}{3}\)m/sec
Length of train = Speed × Time
=\( \frac{50}{3}\)*30= 500 m

Q.10

A train passes two persons walk- ing in the same direction at a speed of 3 km/hour and 5km/ hour respectively in 10 seconds and 11 seconds respectively. The speed of the train is

(1) 28 km/hour

(2) 27 km/hour

(3) 25 km/hour

(4) 24 km/hour

Ans .

(3) 25 km/hour

Explanation :

Let the speed of train be x kmph and its length be y km. When the train crosses a man, it covers its own length According to he question,
\( \frac{y}{(x-3)*\frac{5}{18}}\)=10
18 y = 10 × 5(x –3)
18y = 50x –150
and \( \frac{y}{(x-3)*\frac{5}{18}}\)=11
18y = 55(x–5)
18y = 55x –275
From equations (i) and (ii),
55x –275 = 50x–150
55x –50x = 275 – 150
5x = 125
x=25
Speed of the train = 25 kmph

Q.11

A passenger train 150m long is travelling with a speed of 36 km/ hr. If a man is cycling in the di- rection of train at 9 km/hr., the time taken by the train to pass the man is

(1) 10 sec

(2) 15 sec

(3) 18 sec

(4) 20 sec

Ans .

(3) 20 sec

Explanation :

Relative speed of train = (36 – 9) kmph = 27 kmph
=\( \frac{27*5}{18}\)m/sec
=\( \frac{15}{2}\)m/sec
Required time \( \frac{Length of the train}{Relative speed}\)
=\( \frac{150*2}{15}\)= 20 seconds

Q.12

Buses start from a bus terminal with a speed of 20 km/hr at in- tervals of 10 minutes. What is the speed of a man coming from the opposite direction towards the bus terminal if he meets the buses at intervals of 8 minutes?

(1) 3 km/hr

(2) 4 km/hr

(3) 5 km/hr

(4) 7 km/hr

Ans .

(3) 5 km/hr

Explanation :

Distance covered in 10 min- utes at 20kmph = distance cov- ered in 8 minutes at (20 + x ) kmph
=20*\( \frac{10}{60}\)=\( \frac{8}{60}\)20 + x
200 = 160 + 8x
8x = 40
x=5 kmph

Q.13

A train, 300m long, passed a man, walking along the line in the same direction at the rate of 3 km/hr in 33 seconds. The speed of the train is

(1) 30 km/h

(2) 32 km/h

(3) 35.72 kmph

(4) 27 kmph

Ans .

(3) 35.72 kmph

Explanation :

If the speed of the train be x kmph, then relative speed = (x – 3) kmph.
=\( \frac{300}{x-3*\frac{5}{18}}\)= 33
5400 = 33 × 5 (x – 3)
360 = 11 (x – 3)
11x – 33 = 360
x=\( \frac{393}{11}\)kmph. =35.72kmph

Q.14

A train, 240 m long crosses a man walking along the line in oppo- site direction at the rate of 3 kmph in 10 seconds. The speed of the train is

(1) 63 kmph

(2) 75 kmph

(3) 83.4 kmph

(4) 86.4 kmph

Ans .

(3) 83.4 kmph

Explanation :

If the speed of train be x kmph then, Its relative speed = (x + 3) kmph Time=\( \frac{Length of the train}{Relative speed}\) \( \frac{10}{3600}\)=\( \frac{\frac{240}{1000}}{x+3}\)=\( \frac{240}{1000 ( x + 3 )}\) x + 3 = 86.4 x = 83.4 kmph

Q.15

A train is running at 36 km/hr. If it crosses a pole in 25 seconds, its length is

(1) 248 m

(2) 250 m

(3) 255 m

(4) 260 m

Ans .

(2) 250 m

Explanation :

Speed of train = 36 kmph
\( \frac{36*5}{18}\)m/sec = 10 m/sec.
Length of train
= Speed × time
= 10 × 25 = 250 metre

Q.16

A train is running at a speed of 90 km/hr. If it crosses a signal in 10 sec., the length of the train (in metres) is

(1) 150

(2) 324

(3) 900

(4) 250

Ans .

(4) 250

Explanation :

Speed of train = 90 kmph =\( \frac{90*5}{18}\)metre/second
= 25 metre/second
If the length of the train be x then,
Speed of train
\( \frac{Length of train}{Time taken in crossing the signal}\)
25=\( \frac{x}{10}\)
x = 250 metre

Q.17

A train 100 metres long meets a man going in opposite direction at 5 km/hr and passes him in \( \frac{36}{5}\) seconds. What is the speed of the train (in km/hr) ?

(1) 45 km/hr

(2) 60 km/hr

(3) 55 km/hr

(4) 50 km/hr

Ans .

(1) 45 km/hr

Explanation :

Let speed of train be x kmph Relative speed = (x + 5) kmph Length of train=\( \frac{100}{1000}\)km =\( \frac{1}{10}\)km \( \frac{\frac{1}{10}}{x+5}\)=\( \frac{36}{5 *60 *60}\) \( \frac{1}{10(x+5)}\)=\( \frac{1}{500}\) x + 5 = 50 x = 45 kmph

Q.18

A train, 120 m long, takes 6 sec- onds to pass a telegraph post; the speed of train is

(1) 72 km/hr

(2) 62 km/hr

(3) 55 km/hr

(4) 85 km/hr

Ans .

(1) 72 km/hr

Explanation :

Speed of train =\( \frac{Length of train}{Time taken in crossing the pole}\)=\( \frac{120}{6}\)= 20 m/sec =20*\( \frac{18}{5}\) = 72 kmph

Q.19

A train 300 m long is running with a speed of 54 km/hr. In what time will it cross a tele- phone pole?

(1) 20 seconds

(2) 15 seconds

(3) 17 seconds

(4) 18 seconds

Ans .

(1) 20 seconds

Explanation :

Speed of train = 54 kmph =\( \frac{54*5}{18}\)m/sec = 15 m/sec Required time =\( \frac{Length of trains}{Speed of train}\) =\( \frac{300}{15}\)= 20 seconds

Q.20

A train 180 metres long is run- ning at a speed of 90 km/h. How long will it take to pass a post ?

(1) 8.2 secs

(2) 7.8 secs

(3) 8 secs

(4) 7.2 secs

Ans .

(4) 7.2 secs

Explanation :

Speed of train = 90 kmph
=90*\( \frac{5}{18}\)m/sec.
= 25 m/sec.
When a train crosses a post, it covers a distance equal to its own length
Required time=\( \frac{Distance}{Speed}\)=\( \frac{180}{25}\)= 7.2 seconds

Q.21

If a man walks at the rate of 5 km/hour, he misses a train by 7 minutes. However if he walks at the rate of 6 km/hour, he reach- es the station 5 minutes before the arrival of the train. The dis- tance covered by him to reach the station is

(1) 6 km

(2) 7 km

(3) 6.25 km

(4) 4 km

Ans .

(1) 6 km

Explanation :

Let the required distance be x km.
Difference of time = 7 + 5 = 12
minutes=\( \frac{1}{5}\)hour
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{5}\)-\( \frac{x}{6}\)=\( \frac{1}{5}\)
\( \frac{6x-5x}{30}\)=\( \frac{1}{5}\)
\( \frac{x}{30}\)=\( \frac{1}{5}\)
x=\( \frac{30}{5}\)= 6 km.

Q.22

A train passes an electrical pole in 20 seconds and passes a plat- form 250 m long in 45 seconds. Find the length of the train.

(1) 400m

(2) 200m

(3) 300m

(4) 250m

Ans .

(2) 200m

Explanation :

If the length of train be x metre, then speed of train
\( \frac{x}{20}\)=\( \frac{x+250}{45}\)
\( \frac{x}{4}\)=\( \frac{x+250}{9}\)
9x = 4x + 1000
9x – 4x = 1000
5x = 1000
x=\( \frac{1000}{5}\)
= 200 metre

Q.23

A train is 250m long. If the train takes 50 seconds to cross a tree by the railway line, then the speed of the train in km/hr is :

(1) 10

(2) 9

(3) 5

(4) 18

Ans .

(4) 18

Explanation :

Speed of train
\( \frac{Length of train}{Time taken in crossing}\)
\( \frac{250}{50}\)= 5 m/sec.
5*\( \frac{18}{5}\)kmph
= 18 kmph

Q.24

A train 150m long passes a km stone in 30 seconds and another train of the same length travel- ling in opposite direction in 10 seconds. The speed ot the sec- ond train is :

(1) 90 km/hr

(2) 125 km/hr

(3) 25 km/hr

(4) 75 km/hr

Ans .

(1) 90 km/hr

Explanation :

Speed of train A \( \frac{150}{30}\)= 5 m/sec.
Speed of train B = x m/sec.
Relative speed = (5+x) m/sec. \ Length of both trains = Rela- tive speed × Time 300 = (5 + x) × 10
5 + x =\( \frac{300}{10}\)= 30
x = 30 – 5 = 25 m/sec.
\( \frac{25*18}{5}\)kmph.
= 90 kmph.

Q.25

The time taken by a train 160 m long, running at 72 km/hr, in crossing an electric pole is

(1) 8 seconds

(2) 9 seconds

(3) 6 seconds

(4) 4 seconds

Ans .

(1) 8 seconds

Explanation :

Distance covered in crossing a pole = Length of train
Speed of train = 72 kmph
\( \frac{72*5}{18}\)m./sec.
= 20 m./sec.
Required Time,\( \frac{160}{20}\)
= 8 seconds

Q.26

In what time will a 100 metre long train running with a speed of 50 km/hr cross a pillar ?

(1) 7.0 seconds

(2) 72 seconds

(3) 7.2 seconds

(4) 70 seconds

Ans .

(3) 7.2 seconds

Explanation :

Speed of train = 50 kmph
\( \frac{50*5}{18}\)m./sec.
\( \frac{125}{9}\)m./sec.
Required Time:\( \frac{\frac{100}{125}}{9}\)seconds
\( \frac{100*9}{125}\)seconds
=7.2seconds

Q.27

A train 150m long passes a tele- graphic post in 12 seconds. Find the speed of the train.(in km/hr)

(1) 50

(2) 12.5

(3) 25

(4) 45

Ans .

(4) 45

Explanation :

Distance covered by train in crossing a telegraphic post = length of train..
Speed of Train=\( \frac{Distance}{Time}\)
=\( \frac{150}{12}\)m/sec
=\( \frac{150}{12}\)*\( \frac{18}{5}\)kmph
= 45 kmph

Q.28

In what time will a train, 60 me- tre long, running at the rate of 36 km/hr pass a telegraph post ?

(1) 9 seconds

(2) 8 seconds

(3) 7 seconds

(4) 6 seconds

Ans .

(4) 6 seconds

Explanation :

Speed of train = 36 kmph
\( \frac{36*5}{18}\)m./sec
= 10 m./sec.
Required time
\( \frac{Length of train}{Speed of train}\)
=\( \frac{60}{10}\)= 6 seconds

Q.29

A train 240 metres in length crosses a telegraph post in 16 seconds. The speed of the train is

(1) 50 km/hr

(2) 52 km/hr

(3) 54 km/hr

(4) 56 km/hr

Ans .

(3) 54 km/hr

Explanation :

When a train crosses a pole it travels a distance equal to its length.
Speed of train
\( \frac{240}{16}\)= 15 m./sec.
15 *\( \frac{18}{5}\)kmph
= 54 kmph.

Q.30

How long does a train, 75 metre long, moving at 60 km/hr take to pass a certain telegraph post?

(1) 3.5 seconds

(2) 4.5 seconds

(3) 5 seconds cannot survive.

(4) 5.4 seconds

Ans .

(2) 4.5 seconds

Explanation :

Distance covered by train = Length of train
Speed of train = 60 kmph
\( \frac{60*5}{18}\)m./sec.
\( \frac{50}{3}\)m./sec.
Required Time=\( \frac{Distance}{Speed}\)
\( \frac{75}{\frac{50}{3}}\)sec
\( \frac{75*3}{50}\)seconds
= 4.5 seconds

Q.31

A train 100 metre long is running at a speed of 120 km/hr. The time taken to pass a person standing near the line is

(1) 1 second

(2) 3 seconds

(3) 5 seconds

(4) 7 seconds

Ans .

(2) 3 seconds

Explanation :

Speed of train = 120 kmph. \( \frac{120*5}{18}\)m./sec. \( \frac{100}{3}\)m./sec. Required time =\( \frac{Length of train}{Speed of train}\) \( \frac{100}{ \frac{100}{3}}\)seconds \( \frac{100}{100}\)*3 seconds = 3 seconds

TYPE-4

Q.1

The distance between two cities A and B is 330 km. A train starts from A at 8 a.m. and travels towards B at 60 km/hr. Another train starts from B at 9 a.m. and travels towards A at 75 km/hr.At what time do they meet?

(1) 10 a.m.

(2) 10 : 30 a.m.

(3) 11 a.m.

(4) 11 : 30 a.m.

Ans .

(3) 11 a.m.

Explanation :

Distance travelled by first train in one hour = 60 × 1 = 60km
Therefore, distance between two train at 9 a.m. = 330 – 60 = 270 km
Now, Relative speed of two trains = 60 + 75 = 135 km/hr
Time of meeting of two trains =\( \frac{270}{135}\)= 2 hrs.
Therefore, both the trains will meet at 9 + 2 = 11 A.M.

Q.2

Two men are standing on oppo- site ends of a bridge 1200 metres long. If they walk towards each other at the rate of 5m/minute and 10m/minute respectively, in how much time will they meet each other ?

(1) 60 minutes

(2) 80 minutes

(3) 85 minutes

(4) 90 minute

Ans .

(2) 80 minutes

Explanation :

Men are walking in opposite di- rections. Hence, they will cover the length of bridge at their rela- tive speed.
Required time
\( \frac{1200}{5+10}\) = 80 minutes

Q.3

Two trains, one 160 m and the other 140 m long are running in opposite directions on parallel rails, the first at 77 km an hour and the other at 67 km an hour. How long will they take to cross each other?

(1) 7 seconds

(2) 7.5 seconds

(3) 6 seconds

(4) 11 seconds

Ans .

(2) 7.5 seconds

Explanation :

If two trains be moving in oppo- site directions at rate u and v kmph respectively, then their relative speed
= (u + v) kmph.
Further, if their length be x and
y km. then time taken to cross
each other =\( \frac{x+y}{u+v}\) hours.
Here,
Total length = 160 + 140
= 300m.
Relative speed = (77 + 67) kmph
== 144 kmph = 144*\( \frac{5}{18}\)m/s
Time=\( \frac{300}{40}\)=\( \frac{15}{2}\)=7.5seconds

Q.4

Two trains are running in opposite direction with the same speed. If the length of each train is 120 metres and they cross each other in 12 seconds, the speed of each train (in km/hour) is

(1) 72

(2) 10

(3) 36

(4) 18

Ans .

(3) 36

Explanation :

Let the speed of each train be x kmph.
Their relative speed
= x + x = 2x kmph.
Time taken
\( \frac{Total length of trains}{Relative Speed}\)
\( \frac{12}{60*60}\)=\( \frac{240*\frac{1}{1000}}{2x}\)
\( \frac{1}{300}\)=\( \frac{120}{1000x}\)
x=\( \frac{300*120}{1000}\)=36
The required speed = 36 kmph.

Q.5

Two trains 140 m and 160 m long run at the speed of 60 km/ hour and 40 km/hour respec- tively in opposite directions on parallel tracks. The time (in sec- onds) which they take to cross each other, is :

(1) 10 sec.

(2) 10.8 sec.

(3) 9 sec.

(4) 9.6 sec.

Ans .

(2) 10.8 sec.

Explanation :

Total length of trains
= 140 + 160 = 300 m.
Relative speed = 60 + 40
= 100 kmph
=100*\( \frac{5}{18}\)m/sec
Time taken to cross each other
=\( \frac{300}{\frac{250}{9}}\)=\( \frac{300*9}{250}\)= 10 . 8 sec.

Q.6

Two trains start from stations A and B and travel towards each other at speed of 50 km/hour and 60 km/hour respectively. At the time of their meeting, the second train has travelled 120 km more than the first. The distance be- tween A and B is :

(1) 990 km

(2) 1200 km

(3) 1320 km

(4) 1440 km

Ans .

(3) 1320 km

Explanation :

Let train A start from station A and B from station B.
Let the trains A and B meet after t hours.
Distance covered by train A in t hours = 50t
Distance covered by train B in t hours = 60t km
According to the question,
60t – 50t = 120
t=\( \frac{120}{10}\)= 12 hours.
Distance AB = 50 × 12 + 60 ×
12 = 600 + 720 = 1320 km

Q.7

Two trains are moving on two par- allel tracks but in opposite direc- tions. A person sitting in the train moving at the speed of 80 km/hr passes the second train in 18 sec- onds. If the length of the second train is 1000 m, its speed is

(1) 100 km/hr

(2) 120 km/hr

(3) 140 km/hr

(4) 150 km/hr

Ans .

(2) 120 km/hr

Explanation :

Let the speed of second train be x m/s.
80 km/h=\( \frac{80*5}{18}\)m/s
According to the question
\( \frac{1000}{x+\frac{80*5}{18}}\)=18
1000 = 18x + 400
x=\( \frac{600}{18}\)m/s
\( \frac{600}{18}\)*\( \frac{18}{5}\)km/h = 120 km/h

Q.8

Two trains 105 metres and 90 metres long, runs at the speed of 45 km/hr and 72 km/hr re- spectively, in opposite directions on parallel tracks. The time which they take to cross each other, is

(1) 8 seconds

(2) 6 seconds

(3) 7 seconds

(4) 5 seconds

Ans .

(2) 6 seconds

Explanation :

Length of both trains = 105 + 90 = 195 m.
Relative speed = (45 + 72) = 117 kmph
117*\( \frac{5}{18}\)m/sec
Time taken=\( \frac{195}{\frac{65}{2}}\)=\( \frac{195*2}{65}\)
= 6 seconds

Q.9

Two trains of equal length, run- ning in opposite directions, pass a pole in 18 and 12 seconds. The trains will cross each other in

(1) 14.4 seconds

(2) 15.5 seconds.

(3) 18.8 seconds

(4) 20.2 seconds

Ans .

(1) 14.4 seconds

Explanation :

Let the length of each train be x metre.
Speed of first train =\( \frac{x}{18}\)m/sec
Speed of second train =\( \frac{x}{12}\)m/sec
When both trains cross each oth- er, time taken
=\( \frac{2x}{\frac{x}{18}+\frac{x}{12}}\)
\( \frac{2x}{\frac{2x+3x}{36}}\)=\( \frac{2x*36}{5x}\)
\( \frac{72}{5}\)
= 14.4 seconds

Q.10

A train, 150m long, passes a pole in 15 seconds and another train of the same length travelling in the opposite direction in 12 sec- onds. The speed of the second train is

(1) 45 km./hr

(2) 48 km./hr

(3) 52 km./hr

(4) 54 km./hr

Ans .

(4) 54 km./hr

Explanation :

Let the speed of the second train be x m/s
Speed of first train =\( \frac{150}{15}\)= 10 m/sec
Relative speed of trains = (x + 10) m/s
Total distance covered = 150 + 150 = 300 metre
Time taken = \( \frac{300}{x+10}\)
\( \frac{300}{x+10}\)=12
12x + 120 = 300
12x = 300 – 120 = 180
x=\( \frac{180}{12}\)= 15 m/s
\( \frac{15*18}{5}\)or 54 kmph

Q.11

A train travelling at 48 km/hr crosses another train, having half its length and travelling in oppo- site direction at 42 km/hr, in 12 seconds. It also passes a railway platform in 45 seconds. The length of the railway platform is

1) 200 m

(2) 300 m

(3) 350 m

(4) 400 m

Ans .

(4) 400 m

Explanation :

Let the length of the train travelling at 48 kmph be x metres.
Let the length of the platform be y metres.
Relative speed of train = (48 + 42) kmph
\( \frac{90*5}{18}\)m/sec
= 25 m./sec. and 48 kmph
\( \frac{48*5}{18}\)=\( \frac{40}{3}\)m./sec.
According to the question,
\( \frac{x+\frac{x}{2}}{25}\)=12
\( \frac{3x}{2x*25}\)=12
3x = 2 × 12 × 25 = 600
x = 200 m.
Also,\( \frac{200+y}{\frac{40}{3}}\)=45
600 + 3y = 40 × 45
3y = 1800 – 600 = 1200
y=\( \frac{1200}{3}\)= 400 m.

Q.12

Two towns A and B are 500 km. apart. A train starts at 8 AM from A towards B at a speed of 70 km/ hr. At 10 AM, another train starts from B towards A at a speed of 110 km/hr. When will the two trains meet ?

(1) 1 PM

(2) 12 Noon

(3) 12.30 PM

(4) 1.30 PM.

Ans .

(2) 12 Noon

Explanation :

Let two trains meet after t hours when the train from town A leaves at 8 AM.
Distance covered in t hours at 70 kmph + Distance covered in (t – 2) hours at 110 kmph = 500km
70t + 110 (t – 2) = 500
70t + 110t – 220 = 500
180 t = 500 + 220 = 720
t=\( \frac{720}{180}\)=4 hours
Hence, the trains will meet at 12 noon.

Q.13

Two trains of length 70 m and 80 m are running at speed of 68 km/hr and 40 km/hr respectively on parallel tracks in opposite directions. In how many seconds will they pass each other ?

(1) 10 sec

2) 8 sec

(3) 5 sec

(4) 3 sec

Ans .

(3) 5 sec

Explanation :

Relative speed
= (68 + 40) kmph = 108 kmph
=\( \frac{108*5}{18}\) m/s or 30 m/s
Required time
\( \frac{Sum of the lengths of both trains}{Relative speed}\)
\( \frac{70+80}{30}\)second = 5 seconds

Q.14

Two trains of equal length take 10 seconds and 15 seconds re- spectively to cross a telegraph post. If the length of each train be 120 metres, in what time (in seconds) will they cross each other travelling in opposite direc- tion ?

(1) 16

(2) 15

(3) 12

(4) 10

Ans .

(3) 12

Explanation :

When a train crosses a telegraph post, it covers its own length.
Speed of first train=\( \frac{120}{10}\)= 12 m/sec.
Speed of second train=\( \frac{120}{15}\)= 8 m/sec.
Relative speed = 12 + 8
= 20 m/sec.
Required time
\( \frac{Total length of trains}{Relative speed}\)
=\( \frac{2*120}{20}\)= 12 seconds

Q.15

Two trains of length 137 metre and 163 metre are running with speed of 42 km/hr and 48 km/hr respectively towards each other on papallel tracks. In how many seconds will they cross each other?

(1) 30 sec

(2) 24 sec

(3) 12 sec.

(4) 10 sec

Ans .

(3) 12 sec.

Explanation :

Relative speed = 42 + 48 = 90 kmph
\( \frac{90*5}{18}\)m/s = 25 m/s
Sum of the length of both trains = 137 + 163 = 300 metres
Required time =\( \frac{300}{25}\)= 12 seconds

Q.16

Two trains 150 m and 120 m long respectively moving from oppo- site directions cross each other in 10 secs. If the speed of the second train is 43.2 km/hr, then the speed of the first train is

(1) 54 km/hr

(2) 50 km/hr

(3) 52 km/hr

(4) 51 km/hr

Ans .

(1) 54 km/hr

Explanation :

Speed of second train = 43.2 kmph
=\( \frac{43.2*5}{18}\) m/sec
Let the speed of first train be x m per second, then \( \frac{150 + 120}{x + 12}\)=10
27 = x + 12
x = 15 m/s=15*\( \frac{18}{5}\)kmph = 54 kmph

Q.17

Two trains start from station A and B and travel towards each other at speed of 16 miles/ hour and 21 miles/ hour respectively. At the time of their meeting, the second train has travelled 60 miles more than the first. The dis- tance between A and B (in miles) is :

(1) 444

(2) 496

(3) 333

(4) 540.

Ans .

(1) 444

Explanation :

Let the trains meet after t hours
Then, 21t – 16t = 60
5t = 60 Þ t = 12 hours
Distance between A and B = (16 + 21) × 12
= 37 × 12 = 444 miles

Q.18

Two trains 108 m and 112 m in length are running towards each other on the parallel lines at a speed of 45 km/hr and 54 km/ hr respectively. To cross each other after they meet, it will take

(1) 12 sec

(2) 9 sec

(3) 8 sec

(4) 10 sec

Ans .

(3) 8 sec

Explanation :

Relative speed = 45 + 54
= 99 kmph
99*\( \frac{5}{18}\)m/sec
Required time =\( \frac{108 + 112}{\frac{55}{2}}\)
=\( \frac{220*2}{55}\)= 8 seconds

Q.19

A man standing on a platform finds that a train takes 3 seconds to pass him and another train of the same length moving in the opposite direction, takes 4 sec- onds. The time taken by the trains to pass each other will be

(1) 4.42 sec

(2) 3.45 sec

(3) 3.42 sec

(4) 3.30 sec

Ans .

(3) 3.42 sec

Explanation :

Let the length of each train be x metres
Then, Speed of first train = \( \frac{x}{3}\)m/sec.
Speed of second train =\( \frac{x}{4}\)m/sec.
They are moving in opposite di- rections Relaive speed = \( \frac{x}{3}\)+ \( \frac{x}{4}\)
=\( \frac{4x+3x}{12}\)=\( \frac{7x}{12}\)m/sec
Total length = x + x = 2 x m.
Time taken = \( \frac{2x}{\frac{7x}{12}}\)=\( \frac{24}{7}\)=3.42sec.

Q.20

Two trains, each of length 125 metre, are running in parallel tracks in opposite directions. One train is running at a speed 65 km/hour and they cross each other in 6 seconds. The speed of the other train is

(1) 75 km/hour

(2) 85 km/hour

(3) 95 km/hour

(4) 105 km/hour

Ans .

(2) 85 km/hour

Explanation :

To tal length of both trains = 250 metres
Let speed of second train = x kmph
Relative speed = (65 + x) kmph
=(65 + x )*\( \frac{5}{18}\)m/sec
Time=\( \frac{Sum of length of trains}{Relative speed}\)
6=\( \frac{250}{65 + x * \frac{5}{18}}\)
=6*\( \frac{5}{18}\)*(65 + x ) = 250
65+x=\( \frac{250*3}{5}\)
65 + x = 150
x = 150 – 65 = 85 kmph

Q.21

A train running at the speed of 84 km/hr passes a man walk- ing in opposite direction at the speed of 6 km/hr in 4 seconds. What is the length of train (in metre) ?

(1) 150

(2) 120

(3) 100.

(4) 90

Ans .

(3) 100.

Explanation :

Relative speed = (84 + 6)
= 90 kmph
=90*\( \frac{5}{18}\) m/sec.
= 25 m/sec.
Length of train = Relative speed × Time
= 25 × 4 = 100 metre

Q.22

Two trains X and Y start from Jodhpur to Jaipur and from Jaipur to Jodhpur respectively. After passing each other they take 4 hours 48 minutes and 3 hours 20 minutes to reach Jaipur and Jodhpur respectively. If X is moving at 45 km/hr, the speed of Y is

(1) 60 km/hr

(2) 58 km/hr

(3) 54 km/hr

(4) 64.8 km/hr

Ans .

(3) 54 km/hr

Explanation :

=\( \frac{Speed of X}{Speed of Y}\)
=\( \frac{Time taken by Y}{Time taken by X} ^\frac{1}{2} \)
=\( \frac{45}{y}\)=\( \frac{3 hours 20 min}{4 hours 48 min.} ^\frac{1}{2} \)
=\( \frac{45}{y}\)=\( \frac{200 minutes}{288 minutes.} ^\frac{1}{2} \)
=\( \frac{10}{12}\)
10y = 12 × 45
y=54 kmph.

Q.23

P and Q starting simultaneously from two different places proceed towards each other at a speed of 20 km/hour and 30 km/hour respectively. By the time they meet each other. Q has covered 36 km more than that of P. The distance (in km.) between the two places is

(1) 144

(2) 162

(3) 180

(4) 108

Ans .

(3) 180

Explanation :

Let P and Q meet after t hours.
Distance = speed × time
According to the question,
30t – 20t = 36
10t = 36
t=3.6 hours.
Distance between P and Q
= 30t + 20t
= 50t = (50 × 3.6) km.
= 180 km

Q.24

Two places P and Q are 162 km apart. A train leaves P for Q and simultaneously another train leaves Q for P. They meet at the end of 6 hours. If the former train travels 8 km/hour faster than the other, then speed of train from Q is

(1) 12.5 kmph

(2) 4.5 kmph

(3) 9.5 kmph

(4) 5.5 kmph

Ans .

(3) 9.5 kmph

Explanation :

Speed of train starting from Q = x kmph
Speed of train starting from P = (x + 8) kmph
According to the question, PR + RQ = PQ
(x + 8) × 6 + x × 6 = 162
[Distance = Speed × Time]
6x + 48 + 6x = 162
12x = 162 – 48 = 114
x=\( \frac{114}{12}\)
=9.5 kmph.

Q.25

Two trains start at the same time from A and B and proceed to- ward each other at the speed of 75 km/hr and 50 km/hr respec- tively. When both meet at a point in between, one train was found to have travelled 175 km more than the other. Find the distance between A and B.

(1) 875 km.

(2) 785 km.

(3) 758 km..

(4) 857 km

Ans .

(1) 875 km.

Explanation :

Let the trains meet after t hours.
Distance = Speed × Time
According to the question,
75t – 50t = 175
25t = 175
t=7hours.
Distance between A and B
= 75t + 50t = 125t
= 125 × 7 = 875 km.

Q.26

Two trains of lengths 150m and 180m respectively are running in opposite directions on parallel tracks. If their speeds be 50 km/ hr and 58 km/hr respectively, in what time will they cross each other?

(1) 22 seconds.

(2) 15 seconds.

(3) 30 seconds

(4) 11 seconds.

Ans .

(4) 11 seconds

Explanation :

Relative speed = (50 + 58) kmph
=108*\( \frac{5}{18}\) m/sec
= 30 m/sec
Required time
=\( \frac{Total length of trains}{Relative speed}\)
=\( \frac{150+180}{30}\) sec
=\( \frac{330}{30}\)=11 sec.

Q.27

Two trains start at the same time from Aligarh and Delhi and pro- ceed towards each other at the rate of 14 km and 21 km per hour respectively. When they meet, it is found that one train has travelled 70 km more than the other. The distance between two stations is

(1) 350 km

(2) 210 km

(3) 300 km.

(4) 140 km

Ans .

(1) 350 km.

Explanation :

Let the trains meet each other after t hours.
Distance = Speed × Time
According to the question,
21t – 14t = 70
7t = 70
t=10
Required distance
= 21t + 14t = 35t
= 35 × 10 = 350 km.

TYPE-5

Q.1

A train running at \( \frac{7}{11}\) of its own speed reached a place in 22 hours. How much time could be saved if the train would run at its own speed?

(1) 14 hours

(2) 7 hours

(3) 8 hours

(4) 16 hours

Ans .

(3) 8 hours

Explanation :

Since the train runs at \( \frac{7}{11}\)of its own speed, the time it takes is \( \frac{11}{7}\)of its usual speed.Let the usual time taken be t hours.
Then we can write,\( \frac{11}{7}\)t = 22
t=14 hours
Hence, time saved
= 22 – 14 = 8 hours

Q.2

A man with \( \frac{3}{5}\) of his usual speed reaches the destination \( \frac{5}{2}\) hours late. Find his usual time to reach the destination.

(1) 3.75 hours

(2) 7.5 hours

(3) 8 hours

(4) 16 hours

Ans .

(1) 3.75 hours

Explanation :

\( \frac{3}{5}\)of usual speed will take \( \frac{5}{3}\)of usual time. time & speed are inversely
proportional \( \frac{5}{3}\) of usual time
= usual time + \( \frac{5}{2}\)
=\( \frac{2}{3}\) of usual time = \( \frac{5}{2}\)
usual time
\( \frac{5}{2}\) * \( \frac{3}{2}\)=\( \frac{15}{4}\)=3.75 hours.

Q.3

A car travelling with \( \frac{5}{7}\) of its usual speed covers 42 km in 1 hour 40 min 48 sec. What is the usual speed of the car?

(1) 35 kmph

(2) 7 kmph

(3) 25 kmph

(4) 16 kmph

Ans .

(1) 35 kmph

Explanation :

1 hr 40 min 48 sec
1 hr 40 + \( \frac{48}{60}\)
1 hr 40 + \( \frac{4}{5}\)
1 hr \( \frac{204}{5}\)
1 + \( \frac{204}{300}\)hr=\( \frac{504}{300}\)hr
Speed = \( \frac{42}{\frac{504}{300}}\)= 25 kmph
Now \( \frac{5}{7}\)*usual speed = 25
Usual speed = \( \frac{25*7}{5}\)= 35 kmph

Q.4

Walking at three-fourth of his usual speed, a man covers a cer- tain distance in 2 hours more than the time he takes to cover the distance at his usual speed. The time taken by him to cover the distance with his usual speed is

(1) 4.5 hours

(2) 5.5 hours

(3) 6 hours

(4) 5 hours

Ans .

(3) 6 hours

Explanation :

\( \frac{4}{3}\)× usual time – usual time = 2
\( \frac{1}{3}\)usual time = 2
Usual time = 2 × 3 = 6 hours

Q.5

By walking at \( \frac{3}{4}\)of his usual speed, a man reaches his office 20 minutes later than his usual time. The usual time taken by him to reach his office is

(1) 75 minutes

(2) 60 minutes

(3) 40 minutes

(4) 30 minutes

Ans .

(2) 60 minutes

Explanation :

\( \frac{4}{3}\)of usual time
= Usual time + 20 minutes
\( \frac{1}{3}\)of usual time = 20 minutes
Usual time = 20 × 3
= 60 minutes

Q.6

Walking at \( \frac{3}{4}\) of his usual speed, a man is \( \frac{3}{2}\) hours late. His usual time to cover the same distance, (in hours) is

(1) 14 hours

(2) 4.5 hours

(3) 8 hours

(4) 16 hours

Ans .

(2) 4.5 hours

Explanation :

Time and speed are inversely proportional.
\( \frac{4}{3}\)of usual time –usual time
=\( \frac{3}{2}\)
\( \frac{1}{3}\) * usual time= \( \frac{3}{2}\)
Usual time=\( \frac{3*3}{2}\)=\( \frac{9}{2}\)=4.5 hours

Q.7

Walking at \( \frac{6}{7}\) of his usual speed a man is 25 minutes late. His usual time to cover this dis- tance is

(1) 2 hours 30 minutes

(2) 2 hours 15 minutes

(3) 2 hours 25 minutes

(4) 2 hours 10 minutes

Ans .

(1) 2 hours 30 minutes

Explanation :

Time and speed are inversely proportional.
\( \frac{7}{6}\)* Usual time – Usual time
= 25 minutes
Usual time \( \frac{7}{6}\)-1
= 25 minutes
Usual time × \( \frac{1}{6}\)
= 25 minutes
Usual time = 25 × 6
= 150 minutes
= 2 hours 30 minutes

Q.8

Walking \( \frac{6}{7}\) th of his usual speed, a man is 12 minutes late. The usual time taken by him to cover that distance is

(1) 1 hour

(2) 1 hour 12 minutes

(3) 1 hour 15 minutes

(4) 1 hour 20 minutes

Ans .

(2) 1 hour 12 minutes

Explanation :

Time and speed are inversely proportional.
Usual time * \( \frac{7}{6}\)– usual time
= 12 minutes
Usual time * \( \frac{1}{6}\)= 12 minutes
Usual time = 72 minutes
= 1 hour 12 minutes

Q.9

A car travels from P to Q at a constant speed. If its speed were increased by 10 km/h, it would have been taken one hour less- er to cover the distance. It would have taken further 45 minutes lesser if the speed was further increased by 10 km/h. The dis- tance between the two cities is

(1) 540 km

(2) 420 km

(3) 600 km

(4) 620 km

Ans .

(2) 420 km

Explanation :

Fixed distance = x km and certain speed = y kmph (let).
Case I,
\( \frac{x}{y+10}\)=\( \frac{x}{y}\) - 1
=\( \frac{x}{y+10}\) + 1=\( \frac{x}{y}\) .....(1)
Case II,
\( \frac{x}{y+20}\) = \( \frac{x}{y}\) -1 -\( \frac{3}{4}\)
=\( \frac{x}{y}\)- \( \frac{4+3}{4}\)
\( \frac{x}{y+20}\)+\( \frac{7}{4}\)=\( \frac{x}{y}\).....(2)
From equations (i) and (ii),
\( \frac{x}{y+10}\)+1=\( \frac{x}{y+20}\)+\( \frac{7}{4}\)
\( \frac{x}{y+10}\)-\( \frac{x}{y+20}\)=\( \frac{7}{4}\)-1
x*( \frac{y + 20 - y - 10}{y + 10 )( y + 20 )} )
\( \frac{7-4}{4}\)=\( \frac{3}{4}\)
\( \frac{x *10}{( y + 10 )( y + 20 )}\)=\( \frac{3}{4}\)
3 (y + 10) (y + 20) = 40 x
\( \frac{3 ( y + 10 )( y + 20 )}{40}\)=x...(3)
From equation (i),
\( \frac{3 ( y + 10 )( y + 20 )}{40(y+10)}\) + 1
\( \frac{3 ( y + 10 )( y + 20 )}{40y}\)
3 (y +20) + 40
\( \frac{3 ( y + 10 )( y + 20 )}{y}\)
3y 2 + 60y + 40 y = 3(y 2 + 30y + 200)
3y 2 + 100y = 3y 2 + 90y + 600
10y = 600 Þ y = 60
Again from equation (i),
\( \frac{x}{y+10}\)+1=\( \frac{x}{y}\)
\( \frac{x}{60+10}\)+1=\( \frac{x}{60}\)
\( \frac{x}{70}\)+1=\( \frac{x}{60}\)
\( \frac{x+70}{70}\)+1=\( \frac{x}{60}\)
6x + 420 = 7x
7x – 6x = 420
x = 420 km.

Q.10

A car covers four successive 7 km distances at speeds of 10 km/hour, 20 km/hour, 30 km/ hour and 60 km/hour respec- tively. Its average speed over this distance is

(1) 30 km/hour

(2) 20 km/hour

(3) 60 km/hour

(4) 40 km/hour

Ans .

(2) 20 km/hour

Explanation :

Total distance
= 7 × 4 = 28 km.
Total time
\( \frac{7}{10}\)+\( \frac{7}{20}\)+\( \frac{7}{30}\)+\( \frac{7}{60}\) hours
\( \frac{42 + 21 + 14 + 7}{60}\)hours
=\( \frac{84}{60}\)hours=\( \frac{7}{5}\)hours
Average speed
=\( \frac{Total distance}{Total time}\)=\( \frac{28}{\frac{7}{5}}\)kmph
=20 kmph

Q.11

A car goes 20 metres in a sec-ond. Find its speed i n km/hr.

(1) 18

(2) 72

(3) 36

(4) 20

Ans .

(2) 72

Explanation :

1 m/sec = \( \frac{18}{5}\) kmph
20 m/sec =\( \frac{20*18}{5}\)
= 72 kmph

Q.12

The speed of a car is 54 km/hr. What is its speed in m/sec?

(1) 15 m/sec

(2) 19 - 44 m/sec

(3) 194.4 m/sec

(4) 150 m/sec

Ans .

(1) 15 m/sec

Explanation :

1 kmph =\( \frac{5}{18}\)m/sec
54 kmph =\( \frac{5}{18}\)*54
= 15 m/sec.

Q.13

A car covers a certain distance in 25 hours. If it reduces the speed by \( \frac{1}{5}\) th, the car covers 200 km. less in that time. The speed of car is

(1) 60 km./hr.

(2) 30 km./hr.

(3) 40 km./hr.

(4) 50 km./hr.

Ans .

(3) 40 km./hr.

Explanation :

Speed of car = x kmph.
Distance = Speed × Time
= 25x km.
Case II,
Speed of car =\( \frac{4x}{5}\)kmph
Distance covered =\( \frac{4x}{5}\)*25
= 20x km.
According to the question,
25x – 20x = 200
5x = 200
x=40 kmph.

Q.14

A car moving in the morning fog passes a man walking at 4 km/ h. in the same direction. The man can see the car for 3 minutes and visibility is upto a distance of 130 m. The speed of the car is :

(1) 14 km. per hour

(2) 7.6 km. per hour

(3) 8.6 km. per hour

(4) 6.6 km. per hour

Ans .

(4) 6.6 km. per hour

Explanation :

Speed of car = x kmph.
Relative speed = (x – 4) kmph
Time = 3 minutes =\( \frac{3}{60}\)hour=\( \frac{1}{20}\)hour
Distance = 130 metre
\( \frac{130}{1000}\)km=\( \frac{13}{100}\)km
Relative speed =\( \frac{Distance}{Time}\)
5x – 20 = 13
5x = 20 + 13 = 33
x=6.6 kmph.

TYPE-6

Q.1

A boy rides his bicycle 10km at an average speed of 12 km/hr and again travels 12 km at an average speed of 10 km/hr. His average speed for the entire trip is approximately :

(1) 10.4 km/hr

(2) 10.8 km/hr

(3) 11.0 km/hr

(4) 12.2 km/hr

Ans .

(2) 10.8 km/hr

Explanation :

Total distance = 10 + 12
= 22 km
Total time = \( \frac{10}{12}\)+ \( \frac{12}{10}\)=\( \frac{244}{120}\)hours
Required average speed
\( \frac{Total Distance}{Total Time}\)=\( \frac{22}{\frac{244}{120}}\)=\( \frac{22}{244}\)*120
= 10.8 km/hr.

Q.2

A person travels 600 km by train at 80km/hr, 800 km by ship at 40 km/hr 500 km by aeroplane at 400 km/hr and 100 km by car at 50km/hr. What is the av- erage speed for the entire dis- tance ?

(1) 65.04 km/hr

(2) 61.8 km/hr

(3) 51.0 km/hr

(4) 72.2 km/hr

Ans .

(1) 65.04 km/hr

Explanation :

Total distance = 10 + 12
= 22 km
Total time
\( \frac{600}{80}\)+\( \frac{800}{40}\) +\( \frac{500}{400}\) +\( \frac{100}{50}\)
\( \frac{246}{8}\)hr
Average speed
\( \frac{600 + 800 + 500 + 100}{\frac{246}{8}}\)
\( \frac{2000*8}{246}\)
=65.04 km/hr.

Q.3

A train moves with a speed of 30 kmph for 12 minutes and for next 8 minutes at a speed of 45 kmph. Find the average speed of the train:

(1) 37.5 kmph

(2) 36 kmph

(3) 48 kmph

(4) 30 kmph

Ans .

(2) 36 kmph

Explanation :

Average speed
=\( \frac{Total distance}{Time taken}\)
=\( \frac{30* \frac{12}{60}+45*\frac{8}{60}}{\frac{12}{60}+\frac{8}{60}}\)
= 12 × 3 = 36 kmph

Q.4

A man covers half of his journey at 6km/hr and the remaining half at 3km/hr. His average speed is

(1) 9 km/hr

(2) 4.5 km/hr

(3) 4 km/hr

(4) 3 km/hr

Ans .

(3) 4 km/hr

Explanation :

If the same distance are covered at different speed of x kmph and y kmph, the average speed of the whole journey is given by =\( \frac{2xy}{x+y}\)kmph
Required average speed =\( \frac{36}{9}\)=4 kmph

Q.5

A man goes from A to B at a uni- form speed of 12 kmph and re- turns with a uniform speed of 4 kmph Hi s average speed (in kmph) for the whole journey is :

(1) 8

(2) 7.5

(3) 6

(4) 4.5

Ans .

(3) 6

Explanation :

If two equal distances are cov- ered at two unequal speed of x
kmph and y kmph, then average =\( \frac{2xy}{x+y}\)kmph
=\( \frac{96}{16}\)= 6 kmph

Q.6

A train covers a distance of 3584 km in 2 days 8 hours. If it cov- ers 1440 km on the first day and 1608 km on the second day, by how much does the average speed of the train for the remaining part of the journey differ from that for the entire journey ?

(1) 3 km/hour more

(2) 3 km/hour less

(3) 4 km/hour more

(4) 5 km/hour less

Ans .

(1) 3 km/hour more

Explanation :

Remaining distance
= (3584 – 1440 – 1608) km
= 536 km.
This distance is covered at the rate of \( \frac{536}{8}\)= 67 kmph.
Average speed of whole journey =\( \frac{3584}{56}\)=64 kmph
Required difference in speed = (67 – 64) kmph i.e. = 3 kmph more

Q.7

A man travels a distance of 24 km at 6 kmph. Another distance of 24 km at 8 kmph and a third distance of 24 km at 12 kmph. His average speed for the whole journey (in kmph) is

(1) 8

(2) 10

(3) 11

(4) 12

Ans .

(1) 8

Explanation :

Total distance
= 24 + 24 + 24 = 72 km.
Total time
=\( \frac{24}{6}\)+\( \frac{24}{8}\)+\( \frac{24}{12}\)
= (4 + 3 + 2) hours = 9 hours
\ Required average speed
=\( \frac{Total distance}{Total time}\)=8 kmph

Q.8

A constant distance from Chennai to Bangalore is covered by Ex- press train at 100 km/hr. If it returns to the same distance at 80 km/hr, then the average speed during the whole journey is

(1) 90.20 km/hr

(2) 88.78 km/hr

(3) 88.98 km/hr

(4) 88.89 km/hr

Ans .

(4) 88.89 km/hr

Explanation :

If same distance are covered at two different speed of x and y kmph, the average speed of journey =\( \frac{2xy}{x+y}\)
=\( \frac{2*100*80}{100+80}\)
= 88.89 kmph

Q.9

A person went from A to B at an average speed of x km/hr and returned from B to A at an aver- age speed of y km/hr. What was his average speed during the to- tal journey ?

(1) \( \frac{x+y}{2xy}\)

(2) \( \frac{2xy}{x+y}\)

(3) \( \frac{2}{x+y}\)

(4) \( \frac{1}{x}\)+\( \frac{1}{y}\)

Ans .

(2) \( \frac{2xy}{x+y}\)

Explanation :

Required average speed \( \frac{2xy}{x+y}\)
Since, can be given as corollary If the distance between A and B be z units, then
Average speed =\( \frac{Total speed}{Time taken}\)
\( \frac{z+z}{\frac{z}{x}+\frac{z}{y}}\)
=\( \frac{2xy}{x+y}\)

Q.10

A man goes from Mysore to Ban- galore at a uniform speed of 40 km/hr and co mes b ack to Mysore at a uniform speed of 60 km/hr. His average speed for the whole journey is

(1) 48 km/hr

(2) 50 km/hr

(3) 54 km/hr

(4) 55 km/hr

Ans .

(1) 48 km/hr

Explanation :

Average speed
\( \frac{2xy}{x+y}\)
\( \frac{2*40*60}{40+60}\)
= 48 kmph

Q.11

A man goes from a place A to B at a speed of 12 km/hr and re- turns from B to A at a speed of 18 km/hr. The average speed for the whole journey is

(1) 14*\( \frac{2}{5}\)km/hr

(2) 15 km/hr

(3) 15*\( \frac{1}{2}\) km/hr

(4) 16 km/hr

Ans .

(1) 14*\( \frac{2}{5}\)km/hr

Explanation :

Average speed
\( \frac{2xy}{x+y}\)
\( \frac{2*12*18}{12+18}\)
=14*\( \frac{2}{5}\)

Q.12

One third of a certain journey is covered at the rate of 25 km/ hour, one-fourth at the rate of 30 km/hour and the rest at 50 km/ hour. The average speed for the whole journey is

(1) 35 km/hour

(2) 33*\( \frac{1}{3}\) km/hr

(3) 30 km/hr

(4) 22 km/hr

Ans .

(2) 33*\( \frac{1}{3}\) km/hr

Explanation :

Let the total distance be x km
Total time =\( \frac{\frac{x}{3}}{25}\)+\( \frac{\frac{x}{4}}{30}\)+\( \frac{\frac{5x}{12}}{50}\)
=\( \frac{4x+5x}{300}\)
=\( \frac{3x}{100}\)
Average speed=\( \frac{Distance}{Time}\)
=\(\frac{x}{\frac{3x}{100}}\)
=33*\( \frac{1}{3}\) km/hr

Q.13

A man completes 30 km of a jour- ney at the speed of 6 km/hr and the remaining 40 km of the jour- ney in 5 hours. His average speed for the whole journey is

(1) 7 km/hr

(2) 7.5 km/hr

(3) 8 km/hr

(4) 12 km/hr

Ans .

(1) 7 km/hr

Explanation :

Time taken to cover 30km at 6 kmph=\( \frac{30}{6}\)= 5 hour
Time taken to cover 40 km = 5 hours
\ Average speed=\( \frac{Total Distance}{Time}\)
\( \frac{30+40}{10}\)
=7 km/hr

Q.14

A man covers the journey from a station A to station B at a uni- form speed of 36 km/hr and returns to A with a uniform speed of 45 km/hr. His average speed for the whole journey is :

(1) 40 km/hr

(2) 40.5 km/hr

(3) 41 km/hr

(3) 42 km/hr

Ans .

(1) 40 km/hr

Explanation :

Here same distances are covered at different speeds.
\ Average speed
\( \frac{2xy}{x+y}\)
=\( \frac{2*36*45}{36+45}\)
=40 kmph

Q.15

The speed of a train going from Nagpur to Allahabad is 100 kmph while its speed is 150 kmph when coming back from Allaha- bad to Nagpur. Then the average speed during the whole journey is :

(1) 120 kmph

(2) 125 kmph

(3) 140 kmph

(4) 135 kmph

Ans .

(1) 120 kmph

Explanation :

Here, the distances are equal.
\ Average speed=\( \frac{2*100*150}{100+150}\)
=120 kmph

Q.16

P travels for 6 hours at the rate of 5 km/ hour and for 3 hours at the rate of 6 km/ hour. The av- erage speed of the journey in km/ hour is

(1) 3*\( \frac{1}{5}\)

(2) 5*\( \frac{1}{3}\)

(3) 1*\( \frac{2}{9}\)

(4) 2*\( \frac{2}{5}\)

Ans .

(2) 5*\( \frac{1}{3}\)

Explanation :

Total distance = 5 × 6 + 3 × 6
= 30 + 18 = 48 km
Total time = 9 hours
\ Average speed
\( \frac{48}{9}\)
=5*\( \frac{1}{3}\)

Q.17

With an average speed of 40 km/ hr, a train reaches its destination in time. If it goes with an average speed of 35 km/hr, it is late by 15 minutes. The total journey is

(1) 30 km

(2) 40 km

(3) 70 km

(4) 80 km

Ans .

(3) 70 km

Explanation :

Let the length of journey be x km, then \( \frac{x}{35}\)-\( \frac{x}{40}\)=\( \frac{15}{60}\)=\( \frac{1}{4}\) x= 70 km

Q.18

A bus covers four successive 3 km stretches at speed of 10 km/ hr, 20 km/hr, 30 km/hr and 60 km/hr respectively. Its average speed over this distance is

(1) 30 km/hr

(2) 25 km/hr

(3) 20 km/hr

(4) 10 km/hr

Ans .

(3) 20 km/hr

Explanation :

Average speed =\( \frac{Distance}{Time}\) =\( \frac{12}{\frac{3}{10}+\frac{3}{20}+\frac{3}{30}+\frac{3}{60}}\) \( \frac{12*60}{3*12}\) =20 km/hr

Q.19

A train travelled at a speed of 35 km/hr for the first 10 minutes and at a speed of 20 km/hr for the next 5 minutes. The average speed of the train for the total 15 minutes is

(1) 30 km/hr

(2) 23 km/hr

(3) 31 km/hr

(4) 29 km/hr

Ans .

(1) 30 km/hr

Explanation :

Distance covered 35*\( \frac{10}{60}\)+20*\( \frac{5}{60}\)
=\( \frac{45}{6}\)km
Total time = 15 minutes=\( \frac{1}{4}\)hr
Required average speed =\( \frac{Distance}{Time}\)
=30 kmph

Q.20

On a journey across Kolkata, a taxi averages 50 km per hour for 50% of the distance, 40 km per hour for 40% of it and 20 km per hour for the remaining. The average speed (in km/hour) for the whole journey is :

(1) 42

(2) 40

(3) 35

(4) 45

Ans .

(2) 40

Explanation :

Total distance = 100 km.
Total time \( \frac{50}{50}\)+\( \frac{40}{40}\)+\( \frac{10}{20}\)
=\( \frac{5}{2}\)hr
Average speed =\( \frac{100*2}{5}\)
= 40

Q.21

A train goes from Ballygunge to Sealdah at an average speed of 20 km/hour and comes back at an average speed of 30 km/hour. The average speed of the train for the whole journey is

(1) 27 km/hr

(2) 26 km/hr

(3) 25 km/hr

(4) 24 km/hr

Ans .

(4) 24 km/hr

Explanation :

Required average speed \( \frac{2*30*20}{30+20}\)
= 24 km/hr

Q.22

A and B are 20 km apart. A can walk at an average speed of 4 km/ hour and B at 6 km/hr. If they start walking towards each other at 7 a.m., when they will meet ?

(1) 8.00 a.m.

(2) 8.30 a.m.

(3) 9.00 a.m.

(4) 10.00 a.m.

Ans .

(3) 9.00 a.m.

Explanation :

If A and B meet after t hours, then
4 t + 6 t = 20
10 t = 20
t = 2 hr
Hence, both will meet at 9 a.m.

Q.23

A train runs from Howrah to Ban- del at an average speed of 20 km/ hr and returns at an average speed of 30 km/hr. The average speed (in km/hr) of the train in the whole journey is

(1) 20

(2) 22.5

(3) 24

(4) 25

Ans .

(3) 24

Explanation :

Average speed =\( \frac{2*20*30}{20+30}\)
= 24

Q.24

A motorist travels to a place 150 km away at an average speed of 50 km/hr and returns at 30 km/ hr. His average speed for the whole journey in km/hr is

(1) 37.5

(2) 37

(3) 35

(4) 40

Ans .

(1) 37.5

Explanation :

Average speed of whole journey \( \frac{2*50*30}{50+30}\)
= 37.5 kmph

Q.25

A man walks from his house at an average speed of 5 km per hour and reaches his office 6 minutes late. If he walks at an average speed of 6 km/h he reaches 2 minutes early. The dis- tance of the o ffice from his house is

(1) 6 km

(2) 4 km

(3) 5 km

(4) 12 km

Ans .

(2) 4 km

Explanation :

Required distance of office from house = x km. (let)
Time =\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{5}\)-\( \frac{x}{6}\)=\( \frac{2}{15}\)
\( \frac{x}{30}\)=\( \frac{2}{15}\)
x= 4 km

Q.26

A train runs at an average speed of 75 km/hr. If the distance to be covered is 1050 kms, how long will the train take to cover it ?

(1) 13 hrs

(2) 12 hrs

(3) 15 hrs

(4) 14 hrs

Ans .

(4) 14 hrs

Explanation :

Time =\( \frac{Distance}{Speed}\)=\( \frac{1050}{75}\)
= 14 hrs

Q.27

A train travels 500 m in first minute. In the next 4 minutes, it travels in each minute 125 m more than that in the previous minute. The average speed per hour of the train during those 5 minutes will be

(1) 30 km/hr

(2) 45 km/hr

(3) 50 km/hr

(4) 55 km/hr

Ans .

(2) 45 km/hr

Explanation :

Total distance covered by train in 5 minutes
= (500 + 625 + 750 + 875 + 1000)
metre = 3750 metre
= 3.75 km.
Time = 5 minutes =\( \frac{5}{60}\)=\( \frac{1}{12}\)hr
Speed of train=\( \frac{3.75}{\frac{1}{12}}\)
= (3.75 × 12) kmph
= 45 kmph

Q.28

A man covers a total distance of 100 km on bicycle. For the first 2 hours, the speed was 20 km/ hr and for the rest of the jour- ney, it came down to 10 km/hr. The average speed will be

(1) 12\( \frac{1}{2}\) km/hr

(2) 13 km/hr

(3) 20 km/hr

(4) 12 km/hr

Ans .

(1) 12\( \frac{1}{2}\) km/hr

Explanation :

Distance covered in first 2 hours = 2 × 20 = 40 km.
Remaining distance = 100 – 40 = 60 km.
Time taken in covering 60 km at
10 kmph \( \frac{60}{10}\)=6 hr
Required average speed=\( \frac{Distance}{Time}\)
\( \frac{100}{2+6}\)
=12\( \frac{1}{2}\) km/hr

Q.29

When Alisha goes by car at 50 kmph, she reaches her office 5 minutes late. But when she takes her motorbike, she reaches 3 minutes early. If her office is 25 kms away, what is the approxi- mate average speed at which she rides her motorbike ?

(1) 68 kmph

(2) 62 kmph

(3) 58 kmph

(4) 52 kmph

Ans .

(1) 68 kmph

Explanation :

Difference of time = 5 + 3 = 8 minutes
\( \frac{8}{60}\)=\( \frac{2}{15}\)hr
If the speed of motorbike be x kmph, then
\( \frac{25}{50}\)-\( \frac{25}{x}\)=\( \frac{2}{15}\)
11x = 25 × 30
x=68.18 kmph
x= 68 kmph

Q.30

A man goes to a place on bicycle at speed of 16 km/hr and comes back at lower speed. If the aver- age speed is 6.4 km/hr in total journey, then the return speed (in km/hr) is :

(1) 10

(2) 8

(3) 6

(4) 4

Ans .

(4) 4

Explanation :

Let the speed of cyclist while returning be x kmph.
\ Average speed \( \frac{2*16*x}{16+x}\)
6.4 × 16 + 6.4x = 32x
32x – 6.4x = 6.4 × 16
25.6x = 6.4 × 16
x= 4 kmph

Q.31

A car completed a journey of 400 km in 12\( \frac{1}{2}\) hrs. The first \( \frac{3}{4}\) of the journey was done at 30 km/hr. Calculate the speed for the rest of the journey.

(1) 45 km/hr

(2) 25 km/hr

(3) 40 km/hr

(4) 30 km/hr

Ans .

(3) 40 km/hr

Explanation :

Total distance covered = 400 km. Total time =\( \frac{25}{2 }\)hr \( \frac{3}{4}\)of total journey \( \frac{3}{4}\) * 400 = 300 km. Time=\( \frac{Distance}{Speed}\) \( \frac{300}{30}\)=10 Remaining time =\( \frac{25}{2}\)-10 =\( \frac{5}{2}\) Remaining distance = 100 km. \ Required speed of car \( \frac{100}{\frac{5}{2}}\) =40 km/hr

Q.32

Durga walks 5 km from her home to school in 60 minutes, then bi- cycles back to home along the same route at 15 km per hour. Her sister Smriti makes the same round trip, but does so at half of Durga’s average speed. How much time does Smriti spend on her round trip ?

(1) 120 minutes

(2) 40 minutes

(3) 160 minutes

(4) 80 minutes

Ans .

(3) 160 minutes

Explanation :

Durga’s average speed
\( \frac{2*5*15}{5+15}\)
=\( \frac{15}{2}\) kmph
Distance of School = 5 km.
Smriti’s speed =\( \frac{15}{4}\)
Required time =2*\( \frac{5}{\frac{15}{4}}\)
=\( \frac{8}{3}\)hr
\( \frac{8}{3}\)*60 =160 minutes

Q.33

Gautam travels 160 kms at 32 kmph and returns at 40 kmph. Then his average speed is

(1) 72 kmph

(2) 71.11 kmph

(3) 36 kmph

(4) 35.55 kmph

Ans .

(4) 35.55 kmph

Explanation :

Here, distances are equal.
\ Average speed
\( \frac{2*32*40}{32+40}\)
\( \frac{320}{9}\)
= 35.55 kmph

Q.34

A car travels from A to B at the rate of 40 km/h and returns from B to A at the rate of 60 km/ h. Its average speed during the whole journey is

(1) 48 km/h

(2) 50 km/h

(3) 45 km/h

(4) 60 km/h

Ans .

(1) 48 km/h

Explanation :

Here, distance is same.
Average speed=\( \frac{2xy}{x+y}\)
=\( \frac{2*40*60}{40+60}\)
=48 km/h

Q.35

A bus travels 150 km in 3 hours and then travels next 2 hours at 60 km/hr. Then the average speed of the bus will be

(1) 54 km/hr.

(3) 50 km/hr.

(3) 11.0 km/hr

(4) 60 km/hr.

Ans .

(1) 54 km/hr

Explanation :

Total distance covered by the bus = 150 km. + 2 × 60 km.
= (150 + 120) km.
= 270 km.
\ Average speed=\( \frac{Distance}{Time}\)
\( \frac{270}{5}\)
= 54 km/hr

Q.36

Gautam goes to office at a speed of 12 kmph and returns home at 10 kmph. His average speed is :

(1) 11 kmph

(2) 22 kmph

(3) 10.9 kmph

(4) 12.5 kmph

Ans .

(3) 10.9 kmph

Explanation :

Here distances are same
=\( \frac{2*12*10}{12+10}\)
=\( \frac{240}{22}\)
= 10.9 kmph

Q.37

A man travels 50 km at speed 25 km/h and next 40 km at 20 km/ h and there after travels 90 km at 15 km/h. His average speed is :

(1) 18 kmph.

(2) 25 kmph.

(3) 20 kmph.

(4) 15 kmph.

Ans .

(1) 18 kmph.

Explanation :

Total distance covered
= (50 + 40 + 90) km
= 180 km
Time = \( \frac{Distance}{Speed}\)
Total time taken
\( \frac{50}{25}\)+\( \frac{40}{20}\) +\( \frac{90}{15}\)hours
= (2 + 2 + 6) hours
= 10 hours
Average speed
=\( \frac{Total distance}{Total time taken}\)
=\( \frac{180}{10}\)
=18 kmph

Q.38

At an average o f 80 km/hr Shatabdi Express reaches Ran- chi from Kolkata in 7 hrs. The distance between Kolkata and Ranchi is

(1) 560 km.

(2) 506 km.

(3) 560 m.

(4) 650 m.

Ans .

(3) 560 m.

Explanation :

Distance = Speed × Time
= (80 × 7) km.
= 560 km.

Q.39

To cover a distance of 216 km in 3.2 hours, what should be the average speed of the car in me- tre/second?

(1) 67.5 metre/second

(2) 33.75 metre/second

(3) 37.5 metre/second

(4) 18.75 metre/second

Ans .

(4) 18.75 metre/second

Explanation :

Required speed of car=\( \frac{Distance}{Time}\)
\( \frac{216}{3.2}\)kmph
\( \frac{216}{3.2}\)*\( \frac{5}{18}\)m/sec
= 18.75 m./sec.

TYPE-7

Q.1

In covering a certain distance, the speed of A and B are in the ratio of 3 : 4. A takes 30 minutes more than B to reach the destination. The time taken by A to reach the destination is :

(1) 2 hours

(2) 2.5 hours

(3) 3 hours

(4) 4 hours

Ans .

(1) 2 hours

Explanation :

Let the distance of destination be D km
Let the speed of A = 3x km/hr
then speed of B = 4x km/hr
\ According to question,
\( \frac{D}{3x}\)-\( \frac{D}{4x}\)=30 min
=\( \frac{1}{2}\)hour
\( \frac{D}{12x}\)=\( \frac{1}{2}\)
\( \frac{D}{3x}\)=\( \frac{4}{2}\)= 2 hours
Hence, time taken by A to reach destination = 2hrs.

Q.2

The speed of A and B are in the ratio 3 : 4. A takes 20 minutes more than B to reach a destina- tion. In what time does A reach the destination ?

(1) 1.33 hour.

(1) 2.30 hour.

(1) 1.30 hour..

(1) 1 hour.

Ans .

(1) 1.33 hour..

Explanation :

Ratio of speed = 3 : 4
Ratio of time taken = 4 : 3
Let the time taken by A and B be 4x hours and 3 x hours respec- tively.
Then, 4x–3x =\( \frac{20}{60}\)
x=\( \frac{1}{3}\)
Time taken by A = 4x hours
4*\( \frac{1}{3}\)
=1.33 hour

Q.3

The ratio of length of two trains is 5 : 3 and the ratio of their speed is 6 : 5. The ratio of time taken by them to cross a pole is

(1) 5 : 6.

(2) 11 : 8

(3) 25 : 18

(4) 27 : 16

Ans .

(3) 25 : 18.

Explanation :

Required ratio
\( \frac{5}{6}\):\( \frac{3}{5}\)
\( \frac{5*30}{6}\):\( \frac{30*3}{5}\)
= 25 : 18

Q.5

Two trains started at the same time, one from A to B and the other from B to A. If they arrived at B and A respectively 4 hours and 9 hours after they passed each other, the ratio of the speed of the two trains was

(1) 2 : 1

(2) 3 : 2.

(3) 4 : 3

(4) 5 : 4

Ans .

(2) 3 : 2.

Explanation :

Required ratio of the speed of two trains
= \( \frac{√9}{√4}\)
3 : 2

Q.6

The speed of two trains are in the ratio 6 : 7. If the second train runs 364 km in 4 hours, then the speed of first train is

(1) 60 km/hr

(2) 72 km/hr

(3) 78 km/hr

(4) 84 km/hr.

Ans .

(3) 78 km/hr

Explanation :

Speed of second train
\( \frac{364}{4}\)
= 91 kmph
7x = 91
6x=\( \frac{91}{7x}\)*6x
=78 kmph

Q.7

A truck covers a distance of 550 metres in 1 minute whereas a bus covers a distance of 33 kms in 45 minutes. The ratio of their speed is :

(1) 4 : 3

(2) 3 : 5.

(3) 3 : 4

(4) 50 : 3

Ans .

(3) 3 : 4.

Explanation :

Speed of truck
= 550m/minute
Speed of bus =\( \frac{33000}{45}\)
Required ratio = 550 :\( \frac{2200}{3}\)
=3:4

Q.8

Three cars travelled distance in the ratio 1 : 2 : 3. If the ratio of the time of travel is 3 : 2 : 1, then the ratio of their speed is

(1) 3 : 9 : 1

(2) 1 : 3 : 9

(3) 1 : 2 : 4

(4) 4 : 3 : 2

Ans .

(2) 1 : 3 : 9

Explanation :

Required ratio =\( \frac{1}{3}\):\( \frac{2}{2}\):\( \frac{3}{1}\)
=\( \frac{1}{3}\):1:3
=\( \frac{1}{3}\)*3:1*3:3*3
= 1 : 3 : 9

Q.9

A and B run a 5 km race on a round course of 400 m. If their speed are in the ratio 5 : 4, the number of times, the winner passes the other, is

(1) 1

(2) 2

(3) 3

(4) 5

Ans .

(3) 3

Explanation :

The winner will pass the other, one time in covering 1600m. Hence, the winner will pass the other 3 times in completing 5km race

Q.10

A cyclist, after cycling a distance of 70 km on the second day, finds that the ratio of distance covered by him on the first two days is 4 : 5. If he travels a distance of 42 km. on the third day, then the ratio of distance travelled on the third day and the first day is :

(1) 4 : 3

(2) 3 : 2

(3) 3 : 4

(4) 2 : 3

Ans .

(3) 3 : 4

Explanation :

Distance covered on the first day
\( \frac{4}{5}\)*70= 56 km
Required ratio = 42 : 56
= 3 : 4

Q.11

A certain distance is covered by a cyclist at a certain speed. If a jogger covers half the distance in double the time, the ratio of the speed of the jogger to that of the cyclist is

(1) 1 : 4

(2) 4 : 1

(3) 1 : 2

(4) 2 : 1

Ans .

(1) 1 : 4

Explanation :

Let speed of cyclist = x kmph
& Time = t hours
Distance= \( \frac{xt}{2}\)while time = 2t
Required ratio =\( \frac{xt}{2*2t}\):x
= 1 : 4

Q.12

It takes 8 hours for a 600 km journey, if 120 km is done by train and the rest by car. It takes 20 minutes more if 200 km is done by train and the rest by car. The ratio of the speed of the train to that of the car is

(1) 2 : 3

(2) 3 : 2

(3) 3 : 4

(4) 4 : 3

Ans .

(3) 3 : 4

Explanation :

Speed of train = x kmph
Speed of car = y kmph
Case 1:
\( \frac{120}{x}\)+\( \frac{600-120}{y}\)=8
\( \frac{15}{x}\)+\( \frac{60}{y}\)=1...(1)
Case 2
\( \frac{200}{x}\)+\( \frac{400}{y}\)= 8 hours 20 min
\( \frac{24}{x}\)+\( \frac{48}{y}\)=1...(2)
\( \frac{15}{x}\)+\( \frac{60}{y}\)=\( \frac{24}{x}\)+\( \frac{48}{y}\)
\( \frac{9}{x}\)=\( \frac{12}{y}\)
\( \frac{x}{y}\)=\( \frac{9}{12}\)
=3:4

Q.13

It takes eight hours for a 600 km journey, if 120 km is done by train and the rest by car. It takes 20 minutes more, if 200 km is done by train and the rest by car. The ratio of the speed of the train to that of the car is :

(1) 3 : 5.

(2) 3 : 4

(3) 4 : 3

(4) 4 : 5

Ans .

(2) 3 : 4

Explanation :

Let the speed of train be x kmph. and the speed of car be y kmph
Time=\( \frac{Distance}{Speed}\)
\( \frac{120}{x}\)+\( \frac{480}{y}\)=8
\( \frac{15}{x}\)+\( \frac{60}{y}\)=1.....(1)
\( \frac{200}{x}\)+\( \frac{400}{y}\)=\( \frac{25}{3}\)
\( \frac{24}{x}\)+\( \frac{48}{y}\)=1....(2)
From equations (i) and (ii),
\( \frac{15}{x}\)+\( \frac{60}{y}\)=\( \frac{24}{x}\)+\( \frac{48}{y}\)
\( \frac{x}{y}\)=\( \frac{9}{12}\)
=3:4

Q.14

A truck covers a distance of 550 metre in one minute where as a bus covers a distance of 33 km in \( \frac{3}{4}\) hour. Then the ratio of their speeds is :

(1) 1 : 3 .

(2) 2 : 3

(3) 3 : 4

(4) 1 : 4

Ans .

(3) 3 : 4.

Explanation :

Speed of truck =\( \frac{550 metre}{60 second}\)
\( \frac{55}{6}\)m/sec
Speed of bus =\( \frac{33 * 1000 metre}{\frac{3}{4}*60*60sec}\)
=\( \frac{440}{36}\)
Required ratio =\( \frac{55}{6}\):\( \frac{440}{36}\)
= 55 × 6 : 440
= 3 : 4

Q.15

A car travels 80 km. in 2 hours and a train travels 180 km. in 3 hours. The ratio of the speed of the car to that of the train is :

(1) 2 : 3

(2) 3 : 2

(3) 3 : 4

(4) 4 : 3

Ans .

(1) 2 : 3

Explanation :

Speed =\( \frac{Distance}{Time}\)
Speed of car : Speed of train
=\( \frac{80}{2}\):\( \frac{180}{3}\)
= 40 : 60 = 2 : 3

Q.16

The speeds of three cars are in the ratio of 1 : 3 : 5. The ratio among the time taken by these cars to travel the same distance is

(1) 3 : 5 : 15

(2) 15 : 3 : 5

(3) 15 : 5 : 3

(4) 5 : 3 : 1

Ans .

(3) 15 : 5 : 3

Explanation :

Speed ∝ \( \frac{1}{Time}\)
Required ratio of time
1:\( \frac{1}{3}\):\( \frac{1}{5}\)
=15:\( \frac{1}{3}\)*15:\( \frac{1}{5}\)*15
= 15 : 5 : 3

TYPE-8

Q.1

A thief is noticed by a policeman from a distance of 200m. The thief starts running and the policeman chases him. The thief and the po- liceman run at the rate of 10 km./ hr and 11 km./hr respectively. What is the distance between them after 6 minutes ?

(1) 100 m

(2) 190 m

(3) 200 m

(4) 150 m.

Ans .

(1) 100 m.

Explanation :

Relative speed of police
= 11 – 10 = 1 kmph
=\( \frac{5}{18}\)
Distance decreased in 6 min- =\( \frac{5}{18}\) × 6×60 = 100 m
Distance remained between them = 200–100 = 100 m

Q.2

A moving train, 66 metres long, overtakes another train of 88 metres long, moving in the same direction in 0.168 minutes. If the second train is moving at 30 km/hr, at what speed is the first train moving ?

(1) 85 km/hr.

(2) 50 km/hr.

(3) 55 km/hr.

(4) 25 km/hr

Ans .

(1) 85 km/hr

Explanation :

Suppose the speed of first train be x kmph
Speed of second train
= 30 kmph
\( \frac{30*1000}{60}\)= 500 m per min.
According to question
\( \frac{Total distance}{Relative speed}\)
\( \frac{(66 + 88 )}{x-500}\)=0.168
0.168x – 84 = 154
0.168x = 238
x=\( \frac{238}{0.168}\)
\( \frac{238*1000}{168}\)*\( \frac{3}{50}\)
= 85 kmph

Q.3

A constable is 114 metres be- hind a thief. The constable runs 21 metres and the thief runs 15 metres in a minute. In what time will the constable catch the thief ?

(1) 19 minutes

(2) 18 minutes

(3) 17 minutes

(4) 16 minutes

Ans .

(1) 19 minutes.

Explanation :

The gap of 114 metre will be filled at relative speed. Required time
\( \frac{114}{21-15}\)
=19 minutes

Q.4

How much time does a train, 50 m long, moving at 68 km/ hour take to pass another train, 75 m long, moving at 50 km/ hour in the same direction ?

(1) 5 seconds .

(2) 10 seconds

(3) 20 seconds

(4) 25 seconds

Ans .

(4) 25 seconds.

Explanation :

Both trains are moving in the same direction.
\ Their relative speed
= (68 – 50) kmph = 18 kmph
=18*\( \frac{5}{8}\)= 5 m/sec
Total length = 50 + 75 = 125 m
\ Required time =\( \frac{Total length}{Relative speed}\)=\( \frac{125}{5}\)
=25 seconds.

Q.5

A constable follows a thief who is 200 m ahead of the constable. If the constable and the thief run at speed of 8 km/hour and 7 km/hour respectively, the con- stable would catch the thief in

(1) 10 minutes

(2) 12 minutes

(3) 15 minutes

(4) 20 minutes

Ans .

(2) 12 minutes

Explanation :

The constable and thief are running in the same direction
\ Their relative speed
= 8 – 7 = 1km.
1*\( \frac{5}{18}\)
Required time =\( \frac{200}{\frac{5}{18}}\)
=720 sec
=\( \frac{720}{60}\)
=12 minutes

Q.6

Two trains are running with speed 30 km/hr and 58 km/hr in the same direction. A man in the slower train passes the faster train in 18 seconds. The length (in metres) of the faster train is :

(1) 70

(2) 100.

(3) 128

(4) 140

Ans .

(4) 140

Explanation :

Relative speed
= (58 – 30) km/hr
28*\( \frac{5}{18}\)
\( \frac{70}{9}\)m/sec.
Length of train =\( \frac{70}{9}\)*18
= 140 metres

Q.7

Two trains travel in the same di- rection at the speed of 56 km/h and 29 km/h respectively. The faster train passes a man in the slower train in 10 seconds. The length of the faster train (in me- tres) is

(1) 100.

(2) 80

(3) 75

(4) 120

Ans .

(3) 75.

Explanation :

Relative speed
= 56 – 29 = 27 kmph
27*\( \frac{5}{18}\)
\( \frac{15}{2}\)
Distance covered in 10 sec- onds \( \frac{15}{2}\)*10
= 75 m

Q.8

A bus moving at a speed of 45 km/hr overtakes a truck 150 metres ahead going in the same direction in 30 seconds. The speed of the truck is

(1) 27 km/hr.

(2) 24 km/hr

(3) 25 km/hr

(4) 28 km/hr

Ans .

(1) 27 km/hr

Explanation :

Let the speed of the truck be x kmph
Relative speed of the bus
= 45 - x kmph
Time=\( \frac{Distance}{Relative speed}\)
\( \frac{30}{60*60}\)=\( \frac{\frac{150}{1000}}{45-x}\)
(45 – x ) = 18
x=27 kmph

Q.9

Two trains of equal length are run- ning on parallel lines in the same direction at 46 km/h and 36 km/h. The faster train passes, the slow- er train in 36 seconds. The length of each train is :

(1) 82 m

(2) 50 m

(3) 80 m

(4) 72 m

Ans .

(2) 50 m.

Explanation :

Let the length of each train be x metre.
Relative speed
= 46 – 36 = 10 kmph
=\( \frac{25}{9}\)
=\( \frac{2x}{\frac{25}{9}}\)=36
x = 50 metre

Q.10

Two trains start from a certain place on two parallel tracks in the same direction. The speed of the trains are 45 km/hr and 40 km/ hr respectively. The distance be- tween the two trains after 45 min- utes will be

(1) 2 km 500 m

(2) 2 km 750 m

(3) 3 km 750 m

(4) 3 km 250 m

Ans .

(3) 3 km 750 m

Explanation :

Relative speed
= 45– 40 = 5 kmph
Required distance
5*\( \frac{45}{60}\)
\( \frac{15}{4}\)km
= 3 km 750

Q.11

A boy started from his house by bicycle at 10 a.m. at a speed of 12 km per hour. His elder brother started after 1 hr 15 mins by scooter along the same path and caught him at 1.30 p.m. The speed of the scooter will be (in km/hr)

(1) 4.5

(2) 36.

(3) 18.6

(4) 15

Ans .

(3) 18.6

Explanation :

Let the speed of Scooter be x
Distance covered by cycling in 3\( \frac{1}{2}\)hours = Distance covered
by scooter in 2\( \frac{1}{4}\) hours
12*\( \frac{7}{2}\)=x*\( \frac{9}{4}\)
x=\( \frac{56}{3}\)
= 18.6 kmph

Q.12

A policeman goes after a thief who has 100 metres start, if the policeman runs a kilometre in 8 min, and the thief a km in 10 min, the dis- tance covered by thief before he is over-powered is

(1) 350 m

(2) 400 m

(3) 320 m

(4) 420 m.

Ans .

(2) 400 m

Explanation :

Relative speed
\( \frac{1000}{8}\)-\( \frac{1000}{10}\)=\( \frac{1000}{40}\)
Required time = 4 m/minute
Distance covered by the thief =\( \frac{1000}{10}\)*4
= 400 metres

Q.13

Two trains are running 40 km/hr and 20 km/hr respectively in the same direction. The fast train com- pletely passes a man sitting in the slow train in 5 seconds. The length of the fast train is

(1) 27.7 m

(2) 25 m.

(3) 20 m.

(4) 15 m.

Ans .

(1) 27.7 m

Explanation :

Relative speed = 40 – 20
= 20 km/hour
=\( \frac{20*5}{18}\)
Length of the faster train =\( \frac{250}{9}\)= 27.7 metres

Q.14

A train is moving at a speed of 80 km/h and covers a certain distance in 4.5 hours. The speed of the train to cover the same distance in 4 hours is

(1) 100 km/h.

(2) 70 km/h.

(3) 85 km/h

(4) 90 km/h

Ans .

(4) 90 km/h

Explanation :

Distance = Speed × Time
= 80 × 4.5 = 360 km
Required speed = \( \frac{360}{4}\)
= 90 kmph.

Q.15

Two trains 180 metres and 120 metres in length are running to- wards each other on parallel tracks, one at the rate 65 km/ hour and another at 55 km/hour. In how many seconds will they be clear of each other from the moment they meet ?

(1) 6.

(2) 9

(3) 12

(4) 15

Ans .

(2) 9

Explanation :

Required time =\( \frac{Sum of the lengths of trains}{Relative speed}\)
Relative speed = 65 + 55
= 120 kmph
\( \frac{120*5}{18}\)
Required time = \( \frac{180+120}{\frac{120*5}{18}}\)
= 9 seconds

Q.16

Two trains, of same length, are running on parallel tracks in the same direction with speed 60 km/hour and 90 km/hour respectively. T he l atter completely crosses the former in 30 seconds. The length of each train (in metres) is

(1) 125

(2) 150.

(3) 100

(4) 115

Ans .

(1) 125

Explanation :

When two trains cross each other, they cover distance equal to the sum of their length with relative speed.
Let length of each train = x metre
Relative speed = 90 – 60
= 30 kmph
\( \frac{30*5}{18}\)
=\( \frac{25}{3}\)m/sec
\( \frac{2x}{\frac{25}{3}}\)=30
2x = 250
x = 125 metres

Q.17

Two trains, 80 metres and 120 metres long, are running at the speed of 25 km/hr and 35 km/hr respectively in the same direction on parallel tracks. How many seconds will they take to pass each other ?

(1) 48

(2) 64

(3) 70

(4) 72.

Ans .

(4) 72.

Explanation :

Relative speed = 35 – 25
= 10 kmph
=\( \frac{10*5}{18}\)m/sec
Total length = 80 + 120
= 200 metres
Required time =\( \frac{Sum of the length of trains}{Relative speed}\)
=\( \frac{200*18}{10*5}\)
= 72 seconds

Q.18

A goods train starts running from a place at 1 P.M. at the rate of 18 km/hour. Another goods train starts from the same place at 3 P.M. in the same direction and overtakes the first train at 9 P.M. The speed of the second train in km/hr is

(1) 24

(2) 30

(3) 15

(4) 18.

Ans .

(1) 24

Explanation :

Distance covered by the first goods train in 8 hours = Distance covered by the second goods train in 6 hours.
18 × 8 = 6 * x
x=\( \frac{18*8}{6}\)
= 24 kmph

Q.19

Two trains 125 metres and 115 metres in length, are running to- wards each other on parallel lines, one at the rate of 33 km/ hr and the other at 39 km/hr. How much time (in seconds) will they take to pass each other from the moment they meet ?

(1) 8

(2) 10

(3) 12

(4) 15

Ans .

(3) 12.

Explanation :

Relative speed
= (33 + 39) kmph
= 72 kmph
\( \frac{72*5}{18}\)m/sec
= 20 m/sec.
\ Time taken in crossing
=\( \frac{Length of both trains}{Relative speed}\)
=\( \frac{240}{20}\)
=12 seconds

Q.20

A thief steals a car at 1.30 p.m. and drives it off at 40 km/hr. The theft is discovered at 2 p.m. and the owner sets off in anoth- er car at 50 km/hr. He will over- take the thief at

(1) 5 p.m.

(2) 4 p.m.

(3) 4.30 p.m.

(4) 6 p.m.

Ans .

(2) 4 p.m..

Explanation :

Distance covered by the thief in half an hour =\( \frac{1}{2}\)*40 =20 km
Relative speed of car owner
= 50 – 40 = 10 km
\ Required time
=\( \frac{Difference of distance}{Relative speed}\)
\( \frac{20}{10}\)
= 2 hours
i.e. at 4 p.m.

Q.21

Two trains of equal length are running on parallel lines in the same direction at the rate of 46 km/hr and 36 km/hr. The fast- er train passes the slower train in 36 seconds. The length of each train is

(1) 50 m

(2) 72 m

(3) 80 m

(4) 82 m

Ans .

(1) 50 m

Explanation :

Length of each train = x metre

Relative speed = 46 – 36
= 10 kmph
=\( \frac{10*5}{18}\)
=\( \frac{25}{9}\)m/sec
Time taken in crossing
\( \frac{Length of both trains}{Relative speed}\)
36=\( \frac{2x}{\frac{25}{9}}\)
x = 50 metre

Q.22

Two trains start from stations A and B and travel towards each other at speeds of 50 kmph and 60 kmph respectively. At the time of their meeting, the sec- ond train has travelled 120 km more than the first. The distance between A and B is

(1) 1200 km.

(2) 1440 km

(3) 1320 km

(4) 990 km

Ans .

(3) 1320 km

Explanation :

Let both trains meet after t hours.
\ Distance = speed × time
60t – 50t = 120
10t = 120 t = 12 hours
Required distance
= 60t + 50t
= 110t = 110 × 12
= 1320 km

Q.23

The distance between two plac- es A and B is 60 km. Two cars start at the same time from A and B, travelling at the speeds of 35 km/h and 25 km/h, respective- ly. If the cars run in the same direction, then they will meet af- ter ( in hours)

(1) 6.5

(2) 6.2

(3) 6.

(4) 6.52

Ans .

(3) 6.

Explanation :

Let both cars meet at C after t hours.
Distance covered by car A = AC = 35t km
Distance covered by car B
= BC = 25t km
AC – BC = AB = 60 km.
35t – 25t = 60
10t = 60
t = 6 hours

Q.24

A train ‘B’ speeding with 100 kmph crosses another train C, running in the same direction, in 2 minutes. If the length of the train B and C be 150 metre and 250 metre respectively, what is the speed of the train C (in kmph)?

(1) 75

(2) 88

(3) 95

(4) 110.

Ans .

(2) 88.

Explanation :

Let the speed of train C be x kmph.
Relative speed of B
= (100 – x ) kmph.
Time taken in crossing
\( \frac{Length of both trains}{Relative speed}\)
\( \frac{2}{60}\)=\( \frac{\frac{150+250}{1000}}{100-x}\)
100 – x = 12
x = 100 – 12 = 88 kmph.

Q.25

A passenger train running at the speed of 80 kms./hr leaves the railway station 6 hours after a goods train leaves and overtakes it in 4 hours. What is the speed of the goods train?

(1) 32 kmph

(2) 50 kmph

(3) 45 kmph

(4) 64 kmph

Ans .

(1) 32 kmph

Explanation :

Let the speed of goods train be x kmph.
Distance covered by goods train in 10 hour = distance cov- ered by passenger train in 4 hours
10x = 80 × 4
x = 32 kmph.

Q.26

Two trains start from a certain place on two parallel tracks in the same direction. The speed of the trains are 45 km/hr. and 40 km/ hr respectively. The distance be- tween the two trains after 45 min- utes will be

(1) 2.5 km..

(2) 2.75 km.

(3) 3.7 km.

(4) 3.75 km.

Ans .

(4) 3.75 km..

Explanation :

Relative speed = 45 – 40
= 5 kmph.
Gap between trains after 45 minutes = 5*\( \frac{45}{60}\)
= 3.75 km.

Q.27

A thief is stopped by a policeman from a distance of 400 metres. When the policeman starts the chase, the thief also starts run- ning. Assuming the speed of the thief as 5 km/h and that of po- liceman as 9 km/h, how far the thief would have run, before he is over taken by the policeman ?

(1) 400 metre

(2) 600 metre

(3) 500 metre

(4) 300 metre

Ans .

(3) 500 metre

Explanation :

Distance between thief and policeman = 400 metre
Relative speed of policeman with respect to thief
= (9 – 5) kmph
= 4 kmph
4*\( \frac{5}{18}\)
\( \frac{10}{9}\)m/sec
Time taken in overtaking the thief
\( \frac{400}{\frac{10}{9}}\)
= 360 second
Distance covered by thief
= Speed × Time
=5*\( \frac{5}{18}\)*360
= 500 metre

Q.28

Two trains of equal length are running on parallel lines in the same direction at 46 km/hour and 36 km/hour. The faster train passes the slower train in 36 sec- onds. The length of each train is

(1) 72 m.

(2) 80 m

(3) 82 m

(4) 50 m.

Ans .

(4) 50 m

Explanation :

Let the length of each train be x metre.
Relative speed = (46 – 36) kmph
= 10 kmph
10*\( \frac{5}{18}\)
=\( \frac{25}{9}\)m/sec
\( \frac{2x}{\frac{25}{9}}\)=36
x=50 metre

TYPE-9

Q.1

If a man walks 20 km at 5 km/ hr, he will be late by 40 minutes. If he walks at 8 km/hr, how early from the fixed time will he reach?

(1) 15 minutes

(2) 25 minutes.

(3) 40 minutes

(4) 50 minutes.

Ans .

(4) 50 minutes

Explanation :

Time taken to cover 20 km at the speed of 5km/hr = 4 hours.
\ Fixed time = 4 hours – 40 min- utes
= 3 hour 20 minutes
Time taken to cover 20 km at the speed of 8 km/hr =\( \frac{20}{8}\)=2 hours 30 minutes
Required time = 3 hours 20 minutes – 2 hours 30 minutes = 50 minutes

Q.2

If a man reduces his speed to 2/ 3, he takes 1 hour more in walk- ing a certain distance. The time (in hours) to cover the distance with his normal speed is :

(1) 2

(2) 1.

(3) 3

(4) 1.5

Ans .

(1) 2.

Explanation :

Since man walks at \( \frac{2}{3}\)of usual speed, time taken wil be \( \frac{3}{2}\) usual time.
=usual time + 1 hour.
\( \frac{3}{2}\)-1 of usual time = 1
usual time = 2 hours.

Q.3

A student rides on bicycle at 8 km/hour and reaches his school 2.5 minutes late. The next day he increases his speed to 10 km/ hour and reaches school 5 min- utes early. How far is the school from his house ?

(2) 8 km

(2) 2 km.

(3) 5 km

(3) 8 km

Ans .

(3) 5 km

Explanation :

Let x km. be the required dis- tance.
Difference in time
= 2.5 + 5 = 7.5 minutes
=\( \frac{7.5}{60}\)=\( \frac{1}{8}\)hr
\( \frac{x}{8}\)-\( \frac{x}{10}\)=\( \frac{1}{8}\)
x=\( \frac{40}{8}\)= 5 km.

Q.4

A man covered a certain distance at some speed. Had he moved 3 km per hour faster, he would have taken 40 minutes less. If he had moved 2 km per hour slower, he would have taken 40 minutes more. The distance (in km) is :

(1) 20

(2) 35

(3) 10

(4) 40

Ans .

(4) 40

Explanation :

Let the distance be x km and initial speed be y kmph. According to question,
\( \frac{x}{y}\)-\( \frac{x}{y+3}\)=\( \frac{40}{60}\).....(1)and
\( \frac{x}{y-2}\)-\( \frac{x}{y}\)=\( \frac{40}{60}\)......(2)
From equations (i) and (ii),
\( \frac{x}{y}\)-\( \frac{x}{y+3}\)=\( \frac{x}{y-2}\)-\( \frac{x}{y}\)
3 (y – 2) = 2 (y + 3)
Þ 3y – 6 = 2y + 6
Þ y = 12
From equation (i),\( \frac{x}{12}\)-\( \frac{x}{15}\)=\( \frac{40}{60}\)
x=40
Distance = 40 km.

Q.5

If a train runs at 40 km/hour, it reaches its destination late by 11 minutes. But if it runs at 50 km/ hour, it is late by 5 minutes only. The correct time (in minutes) for the train to complete the journey is

(1) 13

(2) 15

(3) 19

(4) 21

Ans .

(3) 19 .

Explanation :

If the distance be x km, then
\( \frac{x}{40}\)-\( \frac{x}{50}\)=\( \frac{6}{60}\)
x = 20 km.
Required time
\( \frac{20}{40}\)hr-11 mimnutes
= 19 minutes

Q.6

A student walks from his house at speed of 2\( \frac{1}{2}\) km per hour and reaches his school 6 min- utes late. The next day he in- creases his speed by 1 km per hour and reaches 6 minutes be- fore school time. How far is the school from his house ?

(1) 1.75 km

(2)2.75 km.

(3)1.25 km

(4) 1.15 km.

Ans .

(1) 1.75 km

Explanation :

Let the required distance be x km.
Difference of time
= 6 + 6 = 12 minutes = \( \frac{1}{5}\) hr
According to the question,
\( \frac{x}{\frac{5}{2}}\)-\( \frac{x}{\frac{7}{2}}\)=\( \frac{1}{5}\)
\( \frac{14x-10x}{35}\)=\( \frac{1}{5}\)
x=\( \frac{7}{4}\)=1.75 km

Q.7

A boy is late by 9 minutes if he walks to school at a speed of 4 km/hour. If he walks at the rate of 5 km/hour, he arrives 9 min- utes early. The distance to his school is

(1) 9 km.

(2) 5 km

(3) 4 km

(4) 6 km

Ans .

(4) 6 km

Explanation :

Let the required distance be x km.
According to the question,
\( \frac{x}{4}\)-\( \frac{x}{5}\)=\( \frac{18}{60}\)
x=\( \frac{3}{10}\)* 20= 6 km

Q.8

A car can cover a certain distance in 4\( \frac{1}{2}\) hours. If the speed is in creased by 5 km/hour, it would takes \( \frac{1}{2}\) hr less to cover the same distance. Find the slower speed of the car.

(1) 50 km/hour

(2) 40 km/hour.

(3) 45 km/hour

(4) 60 km/hour

Ans .

(2) 40 km/hour.

Explanation :

Let the initial speed of the car be x kmph and the distance be y km.
Then,y=\( \frac{9}{2}\)x
and, y = 4 (x + 5)
9x = 8x + 40
x = 40 kmph

Q.9

Shri X goes to his office by scooter at a speed of 30km/h and reaches 6 minutes earlier. If he goes at a speed of 24 km/h, he reaches 5 minutes late. The distance of his office is

(1) 20 km

(2) 21 km.

(3) 22 km

(4) 24 km.

Ans .

(3) 22 km

Explanation :

Let the distance of office be x km
\( \frac{x}{24}\)-\( \frac{x}{30}\)=\( \frac{11}{60}\)
\( \frac{x}{120}\)=\( \frac{11}{60}\)
x=22 km

Q.10

Walking at 5 km/hr a student reaches his school from his house 15 minutes early and walking at 3 km/hr he is late by 9 minutes. What is the distance between his school and his house ?

(1) 5 km.

(2) 8 km

(3) 3 km

(4) 2 km.

Ans .

(3) 3 km.

Explanation :

Let the required distance be x km.
\( \frac{x}{3}\)-\( \frac{x}{5}\)=\( \frac{24}{60}\)
\( \frac{2x}{3}\)=2
2x = 2 × 3
x = 3 km

Q.11

A student goes to school at the rate of 2\( \frac{1}{2}\) km/h and reaches 6 minutes late. If he travels at the speed of 3 km/h. he is 10 min- utes early. The distance (in km) between the school and his house is

(1) 5

(2) 4

(3) 3 .

(4) 1.

Ans .

(2) 4

Explanation :

Let the required distance be x
km \( \frac{x}{\frac{5}{2}}\)-\( \frac{x}{3}\)=\( \frac{16}{60}\)
\( \frac{6x-5x}{15}\)=\( \frac{4}{15}\)
x = 4 km.

Q.12

When a person cycled at 10 km per hour he arrived at his office 6 minutes late. He arrived 6 mi nutes early, when he increased his speed by 2 km per hour. The distance of his office from the starting place is

(1) 6 km

(2) 7 km.

(3) 12 km.

(4) 16 km

Ans .

(3) 12 km.

Explanation :

Let the distance be x km.
\( \frac{x}{10}\)-\( \frac{x}{12}\)=\( \frac{12}{60}\)
x=\( \frac{1}{5}\)*60
= 12 km.

Q.13

A train covers a distance be- tween station A and station B in 45 minutes. If the speed of the train is reduced by 5 km/hr, then the same distance is covered in 48 mi nutes. The di stance between station A and B is

(1) 60 km

(2) 64 km

(3) 80 km.

(4) 55 km

Ans .

(1) 60 km

Explanation :

Let the distance between stations be x km, then speed of train
=\( \frac{x}{\frac{45}{60}}\)=\( \frac{4x}{3}\)
\( \frac{3x}{4x-15}\)=\( \frac{4}{5}\)
16x – 60 = 15x
x = 60 km

Q.14

A train covers a distance of 10 km in 12 minutes. If its speed is decreased by 5 km/hr, the time taken by it to cover the same dis- tance will be :

(1) 13.33 minutes

(2) 13 minutes

(3) 12 minutes

(4) 11 minutes 20 sec.

Ans .

(1) 13.33 minutes

Explanation :

Speed of train =\( \frac{Distance}{Time}\)=\( \frac{10}{\frac{12}{60}}\)
= 50 kmph
New speed = 45 kmph
Required time =\( \frac{10}{45}\)
\( \frac{2}{9}\)*60 minutes
=\( \frac{40}{3}\)=13.33 minutes.

Q.15

Walking at a speed of 5 km/hr, a man reaches his office 6 minutes late. Walking at 6 km/hr, he reaches there 2 minutes early. The distance of his office is

(1) 4 km

(2) 3 km.

(3) 1 km

(4) 2.5 km

Ans .

(1) 4 km.

Explanation :

Let the distance of the office
be x km, then \( \frac{x}{5}\)-\( \frac{x}{6}\)=\( \frac{8}{60}\)
x = 2 × 2 = 4 km

Q.16

If a boy walks from his house to school at the rate of 4 km per hour, he reaches the school 10 minutes earli er than the scheduled time. However, if he walks at the rate of 3 km per hour, he reaches 10 minutes late. Find the distance of his school from his house.

(1) 5 km

(2) 4 km

(3) 6 km

(4) 4.5 km

Ans .

(2) 4 km.

Explanation :

Let the distance of school be x km,
then \( \frac{x}{3}\)-\( \frac{x}{4}\)=\( \frac{20}{60}\)
\( \frac{x}{12}\)=\( \frac{1}{3}\)
x= 4 km

Q.17

A train travelling at a speed of 55 km/hr travels from place X to place Y in 4 hours. If its speed is increased by 5 km/hr., then the time of journey is reduced by

(1) 25 minutes

(2) 35 minutes.

(3) 20 minutes

(4) 30 minutes

Ans .

(3) 20 minutes

Explanation :

Distance between stations X and
Y = Speed × Time
= 55 × 4 = 220 km.
New speed = 55 + 5 = 60 kmph
Required time =\( \frac{220}{60}\)=\( \frac{11}{3}\)
= 3 hours 40 minutes.
Required answer
= 4 hours – 3 hours 40 minutes
= 20 minutes

Q.18

If a train runs at 70 km/hour, it reaches its destination late by 12 minutes. But if it runs at 80 km/ hour, it is late by 3 minutes. The correct time to cover the jour- ney is

(1) 58 minutes

(2) 2 hours

(3) 1 hour

(4) 59 minutes.

Ans .

(3) 1 hour

Explanation :

Distance of journey = x km
Difference of time = 12 – 3 = 9 minutes
\( \frac{9}{60}\) hr=\( \frac{3}{20}\)hr
\( \frac{x}{70}\)-\( \frac{x}{80}\)=\( \frac{3}{20}\)
\( \frac{x}{56}\)=\( \frac{3}{2}\)
x=84 km
Required correct time \( \frac{84}{70}\)hr-12 minutes
=72 – 12 = 60 minutes
= 1 hour

TYPE-10

Q.1

A train passes a 50 metres long platform in 14 seconds and a man standing on the platform in 10 seconds.The speed of the train is :

(1) 24 km/hr.

(2) 36km/hr

(3) 40 km/hr

(4) 45 km/hr.

Ans .

(4) 45 km/hr

Explanation :

Let the length of train be x me- tres
\ According to question
Speed of the train =\( \frac{x}{10}\)m / sec
Also, the speed of the train \( \frac{x+50}{14}\)m / sec. It passes the platform in 14 seconds]
Both the speeds should be equal, i.e.,
\( \frac{x}{10}\)=\( \frac{x+50}{14}\)
or 14x = 10x + 500
or 14x – 10x = 500
or 4x = 500
\ x = 125 metres
Hence, Speed =\( \frac{125}{10}\)= 12 . 5 m / sec
\( \frac{12.5*18}{5}\)km / hr .
= 45 km/hr.

Q.2

A train passes a man standing on a platform in 8 seconds and also crosses the platform which is 264 metres long in 20 sec- onds. The length of the train (in metres) is :

(1) 188

(2) 176

(3) 175

(4) 96

Ans .

(2) 176

Explanation :

Let length of train be x m
Speed of train \( \frac{x+264}{20}\)
Also, speed of train =\( \frac{x}{8}\)
\( \frac{x}{8}\)=\( \frac{x+264}{20}\)
5x = 2x + 528
5x – 2x = 528
x = 528 ÷ 3 = 176 m

Q.3

A train moves past a telegraph post and a bridge 264 m long in 8 seconds and 20 seconds re- spectively. What is the speed of the train ?

(1) 69.5 km/hr.

(2) 70 km/hr

(3) 79 km/hr

(4) 79.2 km/hr.

Ans .

(4) 79.2 km/hr

Explanation :

Let the length of train be x me- tres.
Then, speed of train when it passes a telegraph post = \( \frac{x}{8}\)m/sec and speed of train, when it passes the bridge =\( \frac{x+264}{20}\)
Clearly,
\( \frac{x}{8}\)=\( \frac{x+264}{20}\)
5x = 2x + 528
3x = 528
x=176 m
Speed of train
\( \frac{176}{8}\)= 22 m/sec
22*\( \frac{18}{5}\)kmph
= 79.2 kmph

Q.4

A person standing on a railway platform noticed that a train took 21 seconds to completely pass through the platform which was 84 m long and it took 9 seconds in passing him. The speed of the train was

(1) 25.2 km/hour.

(2) 32.4 km/hour.

(3) 50.4 km/hour

(4) 75.6 km/hour

Ans .

(1) 25.2 km/hour.

Explanation :

Let the length of train be x metres.
When the train crosses the standing man, its speed = \( \frac{x}{9}\)
When the train crosses the plat- form of length 84 m, its speed \( \frac{x+84}{21}\)
Obviously,\( \frac{x+84}{21}\)=\( \frac{x}{9}\)
21x – 9x = 9 × 84
12x = 9 × 84
x=63 m
Required speed =\( \frac{63}{9}\)=\( \frac{63}{9}\)*\( \frac{18}{5}\)= 25.2 kmph

Q.5

A moving train passes a platform 50 metres long in 14 seconds and a lamp-post in 10 seconds. The speed of the train is

(1) 24 km/hr.

(2) 36 km/hr..

(3) 40 km/hr.

(4)45 km/hr.

Ans .

(4)45 km/hr.

Explanation :

Suppose length of train be x
According to question
\( \frac{x+50}{14}\) = \( \frac{x}{10}\)14x = 10x + 500
4x = 500
x=125 m
Therefore, speed \( \frac{125}{10}\)*\( \frac{18}{5}\)= 45 kmph

Q.6

A train passes a platform 90 me- tre long in 30 seconds and a man standing on the platform in 15 seconds. The speed of the train is :

(1) 12.4 kmph.

(2) 14.6 kmph

(3) 18.4 kmph

(4) 21.6 kmph

Ans .

(4) 21.6 kmph.

Explanation :

Let the length of the train be x
According to the question,
Speed of the train \( \frac{x+90}{30}\)=\( \frac{x}{15}\)
x + 90 = 2x
x = 90 m
Speed of train =\( \frac{90}{15}\)
6 m/s =6*\( \frac{18}{5}\)= 21.6 kmph

Q.7

A moving train crosses a man standing on a platform and a bridge 300 metres long in 10 sec- onds and 25 seconds respective- ly. What will be the time taken by the train to cross a platform 200 metres long ?

(2) 35 seconds

(2) 21 seconds

(3) 20 seconds

(4) 22 seconds

Ans .

(3) 20 seconds.

Explanation :

Let the length of the train be x metre
Speed of train when it crosses man=\( \frac{x}{10}\)
Speed of train when it crosses platform =\( \frac{x+300}{25}\)
According to the question,
Speed of train=\( \frac{x}{10}\)=\( \frac{x+300}{25}\)
25x = 10x + 3000
15x = 3000
x=200 m
Length of train = 200 metre
Speed of train= \( \frac{x}{10}\)=\( \frac{200}{10}\)= 20 m/sce
Time taken in crossing a 200m long platform = \( \frac{200+200}{20}\)= 20 seconds

Q.8

A train passes a platform 110 m long in 40 seconds and a boy standing on the platform in 30 seconds . The l ength of the train is

(1) 100 m.

(2) 110 m

(3) 220 m

(4) 330 m

Ans .

(4) 330 m

Explanation :

Let the length of the train be x metres.
Speed of train in crossing boy = \( \frac{x}{30}\)
Speed of train in crossing platform \( \frac{x+110}{40}\)
According to the question,
\( \frac{x}{30}\)=\( \frac{x+110}{40}\)
4x = 3x + 330
x = 330 metres

Q.9

A train crosses a pole in 15 sec- onds and a platform 100 metres long in 25 seconds. Its length (in metres) is

(1) 50

(2) 100.

(3) 150

(4) 200.

Ans .

(3) 150

Explanation :

Let the length of train be x metre
\( \frac{x}{15}\)=\( \frac{x+100}{25}\)
5x = 3x + 300
2x = 300
x=150 metres

Q.10

Points ‘A’ and ‘B’ are 70 km apart on a highway. A car starts from ‘A’ and another from ‘B’ at the same time. If they travel in the same direction, they meet in 7 hours, but if they travel to- wards each-other, they meet in one hour. Find the speed of the two cars (in km/hr).

(1) 20, 30

(2) 40, 30.

(3) 30, 50

(4) 20, 40.

Ans .

(2) 40, 30

Explanation :

Q.11

Two trains 100 metres and 95 metres long respectively pass each other in 27 seconds when they run in the same direction and in 9 seconds when they run in opposite directions. Speed of the two trains are

(1) 44 km/hr, 22 km/hr

(2) 52 km/hr, 26 km/hr

(3) 36 km/hr. 18 km/hr

(4) 40 km/hr, 20 km/hr

Ans .

(2) 52 km/hr, 26 km/hr

Explanation :

Let the speed of trains be x and y metre/sec respectively,
\( \frac{100+95}{x-y}\)=27
x-y=\( \frac{65}{9}\)..(1)
\( \frac{195}{x+y}\)=9
x+y=\( \frac{195}{9}\)...(2)
By equation (i) + (ii)
2x= \( \frac{65}{9}\)+\( \frac{195}{9}\)=\( \frac{260}{9}\)
x = \( \frac{130}{9}\)m/sec.
\( \frac{130}{9}\)*\( \frac{18}{5}\)kmph = 52 kmph
From equation (ii),
y = \( \frac{65}{9}\)m/sec
\( \frac{65}{9}\)*\( \frac{18}{5}\)
= 26 kmph

Q.12

A train passes by a lamp post on a platform in 7 sec. and passes by the platform completely in 28 sec. If the length of the platform is 390 m, then length of the train (in me- tres) is

(1) 120

(2) 130

(3) 140.

(4) 150.

Ans .

(2) 130.

Explanation :

Let the length of train be x me- tre, then
\ Speed of train
\( \frac{x}{7}\)=\( \frac{x+390}{28}\)
x=\( \frac{390}{3}\)
= 130 metres

Q.13

A train moving at a rate of 36 km/hr. crosses a standing man in 10 seconds. It will cross a platform 55 metres long, in :

(1) 6 seconds

(2) 7 seconds

(3) 15.5 seconds

(4) 7.5 seconds.

Ans .

(3) 15.5 seconds.

Explanation :

Speed of train = 36 kmph
36 * \( \frac{5}{18}\)= 10 m/sec
Length of train = 10 × 10
= 100 metres
Required time= \( \frac{100+55}{10}\)
= 15.5 seconds

Q.14

A train crosses a platform in 30 seconds travelling with a speed of 60 km/h. If the length of the train be 200 metres, then the l ength ( i n metres) of the platform is

(1) 400

(2) 300.

(3) 200

(4) 500

Ans .

(2) 300.

Explanation :

Speed of train = 60 kmph
60*\( \frac{5}{18}\)m/sec. =\( \frac{50}{3}\)m/sec.
If the length of platform be
= x metre, then
Speed of train=\( \frac{Length of (train + platform)}{Time taken in crossing}\)
50 × 10 = 200 + x
x = 500 – 200 = 300 metre

Q.15

A train leaves a station A at 7 am and reaches another station B at 11 am. Another train leaves B at 8 am and reaches A at 11.30 am. The two trains cross one another at

(1) 8:36 am.

(2) 8:56 am.

(3) 9:00 am

(4) 9:24 am

Ans .

(4) 9:24 am

Explanation :

Let both trains meet after t hours since 7 a.m.
Distance between stations A and B = x Km.
\( \frac{x}{4}\)*t+\( \frac{x}{\frac{7}{2}}\)*(t-1)=x
Speed=\( \frac{Distance}{Time}\)
\( \frac{7t+8t-8}{28}\)=1
15 t – 8 = 28
15 t = 28 + 8 = 36
t=2 hours 24 minutes
Required time = 9 :24 a.m.

Q.16

The time for a train of length 110 metre running at the speed of 72 km/hr to cross a bridge of length 132 metre is

(1) 9.8 seconds

(2) 12.1 seconds

(3) 12.42 seconds

(4) 14.3 seconds.

Ans .

(2) 12.1 seconds.

Explanation :

Speed of train = 72 kmph.
\( \frac{72*5}{18}\)m/sec
= 20 m./sec.
Required time
\( \frac{Length of train and bridge}{Speed of train}\)
\( \frac{242}{20}\)
= 12.1 seconds

Q.17

A train 110 metre long is running with a speed of 60 kmph. In what time will it pass a man who is running at 6 kmph in the direc- tion opposite to that in which the train is going ?

(1) 5 seconds .

(2) 6 seconds

(3) 7 seconds

(4) 10 seconds

Ans .

(2) 6 seconds.

Explanation :

Relative speed of train
= (60 + 6) kmph.
\( \frac{66*5}{18}\)m/sec
=\( \frac{55}{3}\)m/sec.
Length of train = 110 metre
Required time =\( \frac{110}{\frac{55}{3}}\)
= 6 seconds

TYPE-11

Q.1

In a one-kilometre race A, B and C are the three participants. A can give B a start of 50 m. and C a start of 69 m. The start, which B can allow C is .

(1) 17 m..

(2) 20 m.

(3) 19 m.

(4) 18 m

Ans .

(2) 20 m.

Explanation :

Let the time taken to complete the race by A,B, and C be x min- utes
Speed of A =\( \frac{1000}{x}\)
B =\( \frac{1000-50}{x}\) =\( \frac{950}{x}\)
C =\( \frac{1000-69}{x}\)= =\( \frac{931}{x}\)
Now, time taken to complete the race by
B=\( \frac{1000}{\frac{950}{x}}\)=\( \frac{1000*x}{950}\)
and distance travelled by C in
\( \frac{1000x}{950}\)min
\( \frac{1000x}{950}\)*\( \frac{931}{x}\)= 980 km.
B can allow C
= 1000 – 980 = 20 m

Q.2

A runs twice as fast as B and B runs thrice as fast as C. The dis- tance covered by C in 72 min- utes, will be covered by A in :

(1) 18 minutes

(2) 24 minutes

(3) 16 minutes.

(4) 12 minutes

Ans .

(4) 12 minutes

Explanation :

Ratio of the speed of A, B and
C = 6 : 3 : 1
Ratio of the time taken
=\( \frac{1}{6}\):\( \frac{1}{3}\):1=1:2:6
Time taken by A
\( \frac{72}{6}\)= 12 minutes

Q.3

In a race of one kilometre, A gives B a start of 100 metres and still wins by 20 seconds. But if A gives B a start of 25 seconds, B wins by 50 metres. The time taken by A to run one kilometre is

(1) 17.24 seconds

(1) 14.24 seconds.

(1) 13.24 seconds

(1) 17.34 seconds

Ans .

(1) 17.24 seconds.

Explanation :

Let A take x seconds in covering
1000m and b takes y seconds According to the question,
x+20=\( \frac{900}{1000}y\)
x+20=\( \frac{9}{10}y\)...(1)
\( \frac{950}{1000}\)x + 25 = y....(2)
From equation (i),
\( \frac{10x}{9}\)+\( \frac{200}{9}\)=y
\( \frac{10x}{9}\)+\( \frac{200}{9}\)=\( \frac{950}{1000}\)x + 25
\( \frac{200x-171x}{180}\)=\( \frac{225-200}{9}\)
\( \frac{29x}{180}\)=\( \frac{25}{9}\)
x=\( \frac{500}{29}\)=17.24

Q.4

In a 100m race, Kamal defeats Bimal by 5 seconds. If the speed of Kamal is 18 Kmph, then the speed of Bimal is

(1) 15.4 kmph

(2) 14.5 kmph.

(3) 14.4 kmph

(4) 14 kmph

Ans .

(3) 14.4 kmph

Explanation :

Time taken by Kamal
\( \frac{100}{18*\frac{5}{18}}\)
= 20 seconds
Time taken by Bimal
= 20 + 5 = 25 seconds
Bimal’s speed = \( \frac{100}{25}\)=4 m/sec
=\( \frac{4*18}{5}\)=14.4 kmph.

Q.5

In a race of 1000 m, A can beat B by 100m. In a race of 400 m, B beats C by 40m. In a race of 500m. A will beat C by

(1) 95 m.

(2) 50 m.

(3) 45 m.

(4) 60 m.

Ans .

(1) 95 m..

Explanation :

When A runs 1000m, B runs 900m.
\ When A runs 500m, B runs 450 m.
Again, when B runs 400m, C runs 360 m.
\ When B runs 450m, C runs
\( \frac{360}{400}\)*450 = 405 metres
Required distance = 500 – 405
= 95 metres

Q.6

In a race of 800 metres, A can beat B by 40 metres. In a race of 500 metres, B can beat C by 5 metres. In a race of 200 metres, A will beat C by

(1) 11.9 metre

(2) 1.19 metre.

(3) 12.7 metre

(4) 1.27 metre

Ans .

(1) 11.9 metre

Explanation :

According to the question,
\ When A runs 800 metres, B runs 760 metres
\ When A runs 200 metres, B runs= \( \frac{760}{800}\)*200= 190 metres
Again, when B runs 500 metres, C runs 495 metres.
\ When B runs 190 metres, C runs =\( \frac{495}{500}\)*190= 188.1 metres
Hence, A will beat C by 200 – 188.1 = 11.9 metres in a race of 200 metres.

Q.7

In a race of 200 metres, B can give a start of 10 metres to A, and C can give a start of 20 me- tres to B. The start that C can give to A, in the same race, is

(1) 30 metres

(2) 25 metres

(3) 29 metres.

(4) 27 metres.

Ans .

(3) 29 metres..

Explanation :

According to the question,
Q When B runs 200 m metres, A runs 190 metres
\ When B runs 180 metres, A runs=\( \frac{190}{200}\)*180= 171 metres When C runs 200m, B runs 180 metres.
Hence, C will give a start to A by = 200 – 171 = 29 metres

Q.8

A can give 40 metres start to B and 70 metres to C in a race of one kilometre How many metres start can B give to C in a race of one kilometre ?

(1) 31.25 metre

(2) 33.25 metre.

(3) 41.25 metre

(4) 21.25 metre.

Ans .

(1) 31.25 metre

Explanation :

According to the question,
When A covers 1000m, B covers = 1000 – 40 = 960 m
and C covers =1000 – 70 = 930 m
When B covers 960m, C covers 930 m.
\ When B covers 1000m, C covers=\( \frac{930}{960}\)*1000 = 968.75 metre
Hence, B gives C a start of = 1000 – 968.75 = 31.25 metre

Q.9

A jeep is chasing a car which is 5km ahead. Their respective speed are 90 km/hr and 75 km/ hr. After how many minutes will the jeep catch the car ?

(1) 18 min..

(2) 20 min.

(3) 24 min.

(4) 25 min.

Ans .

(2) 20 min.

Explanation :

Relative speed
= 95 – 75 = 15 kmph
Required Time=\( \frac{Distance}{Relative speed}\)
\( \frac{5}{15}\)*60
=20 minutes

Q.10

A is twice as fast as B, and B is thrice as fast as C is. The journey covered by C in 1\( \frac{1}{2}\) hours will be covered by A in

(1) 15 minutes

(2) 30 minutes

(3) 1 hour.

(4) 10 minutes

Ans .

(1) 15 minutes

Explanation :

Time taken by C = t hours
Time taken by B =\( \frac{t}{3}\)hours
Time taken by A =\( \frac{t}{6}\)hours
Here,t=\( \frac{3}{2}\)hours
Required time taken by A
\( \frac{3}{\frac{2}{6}}\)=\( \frac{1}{4}\)
\( \frac{1}{4}\)*60= 15 minutes

Q.11

Walking at the rate of 4 kmph a man covers certain distance in 2 hrs 45 min. Running at a speed of 16.5 kmph the man will cover the same distance in how many minutes ?

(1) 50 min..

(2) 40 min..

(3) 35 min.

(4) 45 min.

Ans .

(2) 40 min

Explanation :

2 hours 45 minutes
2 + \( \frac{45}{60}\)hours=\( \frac{11}{4}\)hours
Distance = Speed × Time
4 * \( \frac{11}{4}\)= 11 km.
Time taken in covering 11 km at 16.5 kmph
=\( \frac{11}{16.5}\)
=40 minutes.

Q.12

Sarthak completed a marathon in 4 hours and 35 minutes. The marathon consisted of a 10 km run followed by 20 km cycle ride and the remaining distance again a run. He ran the first stage at 6 km/hr and then cycled at 16 km/ hr. How much distance did Sarthak cover in total, if his speed in the last run was just half that of his first run?

(1) 5 km..

(2) 35 km.

(3) 40 km.

(4) 45 km.

Ans .

(2) 35 km.

Explanation :

Let the total distance be x km.
Time =\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{10}{6}\) +\( \frac{20}{16}\) +\( \frac{x-30}{3}\)=4 \( \frac{35}{60}\)
=4\( \frac{7}{12}\)
\( \frac{5}{3}\) +\( \frac{5}{4}\) +\( \frac{x}{3}\)-10 =\( \frac{55}{12}\)
x=\( \frac{140}{12}\)*3=35 km

Q.13

Walking at \( \frac{3}{4}\) of his usual speed, a man reaches his office 20 minutes late. Then his usual time for walking to his office is :

(1) 1 hour.

(2) 30 minutes.

(3) 45 minutes

(4) 40 minutes

Ans .

(1) 1 hour.

Explanation :

Usual time = x minutes
New time =\( \frac{4x}{3}\)
Speed ∝ \( \frac{1}{Time}\)
According to the question,
\( \frac{4x}{3}\)– x = 20
x= 1hour

Q.14

A is faster than B. A and B each walk 24 km. The sum of their speeds is 7 km/hr and the sum of times taken by them is 14 hours. Then A’s speed is equal to:

(1) 3 km/hr.

(2) 4 km/hr..

(3) 5 km/hr.

(4) 7 km/hr.

Ans .

(2) 4 km/hr.

Explanation :

Let, A’s speed = x kmph.
\ B’s speed = (7 – x) kmph
Time=\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{24}{x}\)+\( \frac{24}{7-x}\)=14
\( \frac{24*7}{x(7-x)}\)=14
x (7 – x) = 12 = 4 × 3 or 3 × 4
Þ x (7 – x) = 4 (7 – 4) or 3 (7 – 3)
Þ x = 4 or 3
\ A’s speed = 4 kmph.

Q.15

Two persons ride towards each other from two places 55 km apart, one riding at 12km/hr and the other at 10 km/hr. In what time will they be 11 km apart?

(1) 2 hours and 30 minutes

(2) 1 hour and 30 minutes.

(3) 2 hours

(4) 2 hours and 45 minutes.

Ans .

(3) 2 hours

Explanation :

Relative speed
= 12 + 10 = 22 kmph Distance covered
= 55 – 11 = 44 km
\ Required time
\( \frac{44}{22}\)
= 2 hours

Q.16

A and B start running at the same time and from the same point around a circle. If A can complete one round in 40 seconds and B in 50 seconds, how many sec- onds will they take to reach the starting point simultaneously ?

(1) 10

(2) 200.

(3) 90

(4) 2000

Ans .

(2) 200.

Explanation :

Required time = LCM of 40
and 50 seconds
= 200 seconds

Q.17

Rubi goes to a multiplex at the speed of 3 km/hr to see a movie and reaches 5 minutes late. If she travels at the speed of 4 km/hr she reaches 5 minutes early. Then the distance of the multiplex from her starting point is

(1) 2 km..

(2) 5 km..

(3) 2 metre

(4) 5 metre.

Ans .

(1) 2 km.

Explanation :

Distance between starting
point and multiplex = x metre
Time =\( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{3}\) -\( \frac{x}{4}\)= \( \frac{5+5}{60}\)
\( \frac{x}{12}\) =\( \frac{1}{6}\)
x=2 km

TYPE-12

Q.1

I walk a certain distance and ride back taking a total time of 37 minutes. I could walk both ways in 55 minutes. How long would it take me to ride both ways?

(1) 9.5 minutes

(2) 19 minutes

(3) 18 minutes

(4) 20 minutes

Ans .

(2) 19 minutes

Explanation :

Two ways walking time = 55 min...(i)
One way walking + One way riding time = 37 min.....(ii)
By 2 × (ii) – (i),
2 ways riding time = 2×37–55 = 19 minutes.

Q.2

A and B start at the same time with speed of 40 km/hr and 50 km/hr respectively. If in covering the journey A takes 15 minutes longer than B, the total distance of the journey is :

(1) 46 km

(2) 48 km

(3) 50 km

(4) 52 km

Ans .

(3) 50 km.

Explanation :

Let the distance be x km
Time taken by A =\( \frac{x}{40}\)hrs
Time taken by B =\( \frac{x}{50}\)hrs
\( \frac{x}{40}\)-\( \frac{x}{50}\)=\( \frac{15}{60}\)
\( \frac{5x-4x}{200}\)=\( \frac{15}{60}\)
x=50 km

Q.3

A man can reach a certain place in 30 hours. If he reduces his speed by \( \frac{1}{15}\) he goes 10 km less in that time. Find his speed per hour.

(1) 5 km/hr

(1) 6 km/hr

(1) 16 km/hr

(1) 7 km/hr.

Ans .

(1) 5 km/hr.

Explanation :

Let the speed of man be x kmph
30 x – 30{x-\( \frac{x}{15}\)} = 10
30{x-x+\( \frac{x}{15}\)}=10
\( \frac{x}{15}\)=\( \frac{10}{30}\)
x= 5kmph

Q.4

A, B and C start at the same time in the same direction to run around a circular stadium. A completes a round in 252 sec- onds, B in 308 seconds and C in 198 seconds, all starting at the same point. After what time will they next meet at the start- ing point again ?

(1) 46 minutes 12 seconds

(2) 45 minutes

(3) 42 minutes 36 seconds

(4) 26 minutes 18 seconds.

Ans .

(1) 46 minutes 12 seconds

Explanation :

Required time = LCM of 252,
308 and 198 seconds.
Now, 252 = 2 × 2 × 3 × 3 × 7
308 = 2 × 2 × 7 × 11
198 = 2 × 3 × 3 × 11
\ LCM = 2 × 2 × 3 × 3 × 7 × 11
= 36 × 77 seconds
\( \frac{36*77}{60}\)minutes
= 46 minutes 12 seconds

Q.5

A man walks a certain distance and rides back in 4 hours 30 minutes. He could ride both ways in 3 hours. The time re- quired by the man to walk both ways is

(1) 4 hours 30 minutes

(2) 4 hours 45 minutes

(3) 5 hours

(4) 6 hours

Ans .

(4) 6 hours

Explanation :

Suppose, time taken while walking be x hours And, time taken on riding be y hours
\ According to question
x+y=4\( \frac{1}{2}\)hr
Then, 2y = 3 hours
y=1\( \frac{1}{2}\)hr
x=4\( \frac{1}{2}\) - 1\( \frac{1}{2}\)=3 hr
Time required to walk both ways = 6 hours

Q.6

A person, who can walk down a hill at the rate of 4\( \frac{1}{2} \) km/hour and up the hill at the rate of 3 km/hour, ascends and comes down to his starting point in 5 hours. How far did he ascend ?

(1) 13.5 km

(2) 3 km

(3) 15 km

(4) 9 km.

Ans .

(4) 9 km

Explanation :

Let the required distance be x km
\( \frac{x}{\frac{9}{2}}\)+\( \frac{x}{3}\)=5
x{\( \frac{2+3}{9}\)=5
x=9 km

Q.7

A walks at a uniform rate of 4 km an hour; and 4 hours after his start, B bicycles after him at the uniform rate of 10 km an hour. How far from the starting point will B catch A ?

(1) 16.7 km.

(2) 18.6 km

(3) 21.5 km

(4) 26.7 km

Ans .

(4) 26.7 km.

Explanation :

Distance covered by A in 4
hours = 4 × 4 = 16 km
Relative speed of B with respect
to A = 10 – 4 = 6 km/hr
Time taken to catch A
\( \frac{16}{6}\)=\( \frac{8}{3}\)hr
Required distance
=\( \frac{8}{3}*10\)
= 26.67 km.= 26.7 km

Q.8

A car completes a journey in 10 hours. If it covers half of the jour- ney at 40 kmph and the remain- ing half at 60 kmph, the distance covered by car is

(1) 400 km.

(2) 480 km.

(3) 380 km

(4) 300 km

Ans .

(2) 480 km.

Explanation :

Suppose distance be x km
\( \frac{x}{2*40}\)+\( \frac{x}{2*60}\)=10
\( \frac{3x+2x}{240}\)=10
x=480 km

Q.9

A and B run a kilometre and A wins by 25 sec. A and C run a kilometre and A wins by 275 m. When B and C run the same dis- tance, B wins by 30 sec. The time taken by A to run a kilometre is

(1) 2 min 25 sec

(2) 2 min 50 sec

(3) 3 min 20 sec

(4) 3 min 30 sec

Ans .

(1) 2 min 25 sec.

Explanation :

If A covers the distance of 1 km in x seconds, B covers the distance of 1 km in (x + 25) sec- onds. If A covers the distance of 1 km, then in the same time C covers only 725 metres.
If B covers 1 km in (x + 25) sec- onds, then C covers 1 km in (x + 55) seconds.
Thus in x seconds, C covers the distance of 725 m.
\( \frac{x}{725}\)*1000=x+55
x = 145
A co vers the di stance of 1 km in 2 minutes 25 seconds.

Q.10

Two cars start at the same time from one point and move along two roads at right angles to each other. Their speeds are 36 km/ hour and 48 km/hour respec- tively. After 15 seconds the dis- tance between them will be

(1) 400 m

(2) 150 m.

(3) 300 m

(4) 250 m.

Ans .

(4) 250 m

Explanation :

Q.11

In a kilometre race, A beats B by 30 seconds and B beats C by 15 seconds. If A beats C by 180 metres, the time taken by A to run 1 kilometre is

(1) 250 seconds

(2) 205 seconds

(3) 200 seconds

(4) 210 seconds

Ans .

(2) 205 seconds

Explanation :

A beats B by 30 seconds and B beats C by 15 seconds. Clearly, A beats C by 45 seconds. Also, A beats C by 180 metres. Hence, C covers 180 metres in 45 seconds
Speed of C =\( \frac{180}{45}\)= 4 m/sec
Time taken by C to cover 1000 m =\( \frac{1000}{4}\)=250 sec
Time taken by A to cover 1000 m = 250–45 = 205 sec

Q.12

Two guns are fired from the same place at an interval of 6 minutes. A person approaching the place observes that 5 minutes 52 sec- onds have elapsed between the hearing of the sound of the two guns. If the velocity of the sound is 330 m/sec, the man was ap- proaching that place at what speed (in km/hr) ?

(1) 24

(2) 27

(3) 30

(4) 36

Ans .

(2) 27.

Explanation :

Difference of time
= 6 min. – 5 min. 52 sec.
= 8 seconds
Distance covered by man in 5 min. 52 seconds
= Distance covered by sound in 8 seconds
= 330 × 8 = 2640 m.
\ Speed of man
\( \frac{2640 m}{5 min. 52 sec.}\)=\( \frac{2640}{352}\)
\( \frac{2640}{352}\)*\( \frac{18}{5}\)kmph
= 27 kmph

Q.13

Ram arrives at a Bank 15 min- utes earlier than scheduled time if he drives his car at 42 km/hr. If he drives car at 35 km/hr he arrives 5 minutes late. The dis- tance of the Bank from his start- ing point is

(1) 70 km

(2) 210 km

(3) 72 km

(4) 15 km.

Ans .

(1) 70 km

Explanation :

Let the required distance be x km.
Difference of time
= 15 + 5 = 20 minutes
=\( \frac{1}{3}\)hr
According to the question,
\( \frac{x}{35}\)-\( \frac{x}{42}\)=\( \frac{1}{3}\)
\( \frac{x}{210}\)=\( \frac{1}{3}\)
x=70 km

Q.14

A and B started at the same time from the same place for a certain destination. B walking at \( \frac{5}{6}\) of A’s speed reached the destination 1 hour 15 minutes after A. B reached the destination in

(1) 6 hours 45 minutes

(2) 7 hours 15 minutes

(3) 7 hours 30 minutes

(4) 8 hours 15 minutes

Ans .

(3) 7 hours 30 minutes

Explanation :

1-\( \frac{5}{6}\) of time taken by B
=1 hour 15 minutes
\ Time taken by B
= 1 hour 15 minutes × 6
=7 hours 30 minutes

Q.15

In covering a distance of 30 km, Abhay takes 2 hours more than Sameer. If Abhay doubles his speed, then he would take 1 hour less than Sameer. Abhay's speed (in km/hr) is

(1) 5

(2) 6

(3) 6.25

(4) 7.5

Ans .

(1) 5

Explanation :

Abhay’s speed = x kmph
Sameer’s speed = y kmph
\( \frac{30}{x}\)-\( \frac{30}{y}\)=12
\( \frac{30}{y}\)-\( \frac{30}{2x}\)=1
On adding,
\( \frac{30}{y}\)-\( \frac{30}{2x}\)=3
\( \frac{30}{2x}\)=3
x = 5 kmph

Q.16

A man takes 6 hours 15 minutes in walking a distance and riding back to the starting place. He could walk both ways in 7 hours 45 minutes. The time taken by him to ride both ways, is

(1) 4 hours

(2) 4 hours 30 minutes

(3) 4 hours 45 minutes

(4) 5 hours

Ans .

(3) 4 hours 45 minutes

Explanation :

Time taken in walking both ways = 7 hours 45 minutes ....(i)
Time taken in walking one way and riding back = 6 hours 15 minutes ....(ii)
By equation (ii) × 2 – (i), we have
Time taken by the man to ride both ways
= 12 hours 30 minutes – 7 hours
45 minutes
= 4 hours 45 minutes

Q.17

A man completed a certain jour- ney by a car. If he covered 30% of the distance at the speed of 20km/hr, 60% of the distance at 40km/hr and the remaining dis- tance at 10km/hr; his average speed for the whole journey was

(1) 25 km/hr

(2) 28 km/hr

(3) 30 km/hr.

(4) 33 km/hr

Ans .

(1) 25 km/hr.

Explanation :

Let the total distance be 100 km.
Average speed
\( \frac{Total distance covered}{Time taken}\)
\( \frac{100}{ \frac{30}{20}+ \frac{60}{40}+ \frac{10}{10}}\)
\( \frac{100*2}{8}\)=25 kmph

Q.18

From two places, 60 km apart, A and B start towards each other at the same time and meet each other after 6 hours. Had A travelled with \( \frac{2}{3}\) of his speed and B travelled with double of his speed, they would have met after 5 hours. The speed of A is

(1) 4 km/hr.

(2) 6 km/hr..

(3) 10 km/hr.

(4) 12 km/hr.

Ans .

(2) 6 km/hr

Explanation :

Let the speed of A = x kmph and that of B = y kmph
According to the question,
x × 6 + y × 6 = 60
x + y = 10
and \( \frac{2}{3}\)x* 5 + 2 y * 5 = 60
10x + 30y = 180
x + 3y = 18 ...(ii)
From equations (i) × (3) – (ii)
3x + 3y – x – 3y = 30 – 18
12x = 12
x = 6 kmph.

Q.19

P and Q are 27 km away. Two trains with speed of 24 km/hr and 18 km/hr respectively start simultaneously from P and Q and travel in the same direction. They meet at a point R beyond Q. Distance QR is

(1) 126 km

(2) 81 km

(3) 48 km

(3) 58 km

Ans .

(2) 81 km

Explanation :

Let the trains meet after t hours, then
24t – 18t = 27
6t = 27
t=\( \frac{9}{2}\)hours
QR = 18t = 18 * \( \frac{9}{2}\)= 81 km

Q.20

Ravi and Ajay start simultaneously from a place A towards B, 60 km apart. Ravi’s speed is 4km/hr less than that of Ajay. Ajay, after reaching B, turns back and meets Ravi at a place 12 km away from B. Ravi’s speed is

(1) 12 km/hr

(2) 10 km/hr

(3) 8 km/hr

(4) 6 km/hr

Ans .

(3) 8 km/hr

Explanation :

Let the speed of Ravi be x kmph
then, Ajay’s speed = (x + 4) kmph
Distance covered by Ajay
= 60 + 12 = 72 km
Distance covered by Ravi
= 60 – 12 = 48 km.
According to the question
\( \frac{72}{x+4}\)=\( \frac{48}{8}\)
\( \frac{3}{x+4}\)=\( \frac{2}{x}\)
3x = 2x + 8
x = 8 kmph

Q.21

A man travelled a distance of 61 km in 9 hours, partly on foot at the rate of 4 km/hr and partly on bicycle at the rate of 9 km/ hr. The distance travelled on foot was

(1) 12 km.

(2) 16 km

(3) 20 km

(4) 24 km

Ans .

(2) 16 km

Explanation :

Let man walked for t hours.
then, t × 4 + (9 – t) × 9 = 61
4t + 81 – 9t = 61
81 – 5t = 61
5t = 20
t = 4
Distance travelled on foot
= 4 × 4 = 16 km.

Q.22

If I walk at 5 km/hour, I miss a train by 7 minutes. If, however, I walk at 6 km/hour, I reach the station 5 minutes before the de- parture of the train. The dis- tance (in km) between my house and the station is

(1) 6.

(2) 5.

(3) 4

(4) 3

Ans .

(1) 6

Explanation :

Let the required distance be x km, then
\( \frac{x}{5}\)-\( \frac{x}{6}\)=\( \frac{1}{5}\)
\( \frac{x}{30}\)=\( \frac{1}{5}\) x=6 km

Q.23

A man has to be at a certain place at a certain time. He finds that he shall be 20 minutes late if he walks at 3 km/hour speed and 10 minutes earlier if he walks at a speed of 4 km/hour. The dis- tance he has to walk is

(1) 24 km

(2) 12·5 km.

(3) 10 km

(4) 6 km.

Ans .

(4) 6 km.

Explanation :

Let the required distance be x km.
\( \frac{x}{3}\)-\( \frac{x}{4}\)=\( \frac{30}{60}\)
\( \frac{x}{12}\)=\( \frac{1}{2}\)
x= 6km

Q.24

Ravi travels 300 km partly by train and partly by car. He takes 4 hours to reach, if he travels 60 km by train and rest by car. He will take 10 minutes more if he were to travel 100 km by train and rest by car. The speed of the train is :

(1) 50 km/hr.

(2) 60 km/hr

(3) 100 km/hr

(4) 120 km/hr.

Ans .

(2) 60 km/hr

Explanation :

Let the speed of train be x kmph and that of car be y kmph, then
\( \frac{60}{x}\)+\( \frac{240}{y}\)=4
and ,\( \frac{100}{x}\)+\( \frac{200}{y}\)=\( \frac{25}{6}\)
\( \frac{4}{x}\)+\( \frac{8}{y}\)=\( \frac{1}{6}\)
By equation (i ) – equation (ii) × 30
\( \frac{60}{x}\)+\( \frac{240}{y}\)-\( \frac{120}{x}\)-\( \frac{240}{y}\)=4-5
-\( \frac{60}{x}\)=-1
x=60 kmph

Q.25

A is twice as fast runner as B, and B is thrice as fast runner as C. If C travelled a distance in 1 hour 54 minutes, the time taken by B to cover the same distance is

(1) 19 minutes

(2) 38 minutes

(3) 51 minutes

(4) 57 minutes

Ans .

(2) 38 minutes.

Explanation :

Ratio of the speed of A and B
= A : B = 2 : 1 = 6 : 3
B : C = 3 : 1
A : B : C = 6 : 3 : 1
Ratio of their time taken
\( \frac{1}{6}\):\( \frac{1}{3}\):1=1:2:6
Time taken by B
\( \frac{2}{6}\)*114 minutes
= 38 minutes

Q.26

Two trains, A and B, start from stations X and Y towards Y and X respectively. After passing each other, they take 4 hours 48 minutes and 3 hours 20 min- utes to reach Y and X respec- tively. If train A is moving at 45 km/hr., then the speed of the train B is

(1) 60 km/hr

(2) 64.8 km/hr

(3) 54 km/hr

(4) 37.5 km/hr

Ans .

(3) 54 km/hr

Explanation :

Q.27

Ram travelled 1200 km by air which formed \( \frac{2}{5}\) of his trip. He travelled one-third of the trip by car and the rest by train. The distance (in km) travelled by train was

(1) 480.

(2) 800

(3) 1600

(4) 1800

Ans .

(2) 800

Explanation :

Total distance of trip
=\( \frac{1200*5}{2}\)= 3000 km
Part of journey covered by train
1-\( \frac{2}{5}\)-\( \frac{1}{3}\)=\( \frac{4}{15}\)
Distance covered by train
3000*\( \frac{4}{15}\)= 800 km

Q.28

A, B, C walk 1 km in 5 minutes, 8 minutes and 10 minutes re- spectively. C starts walking from a point, at a certain time, B starts from the same point 1 minutes later and A starts from the same point 2 minutes later than C. Then A meets B and C after

(1) 1.6 minutes

(2)2.6 minutes.

(3) 2.2 minutes

(4) 1.8 minutes

Ans .

(1) 1.6 minutes

Explanation :

A’s speed =\( \frac{1000}{5}\) = 200 m/minute
B’s speed =\( \frac{1000}{8}\) = 125 m/minute
C’s speed =\( \frac{1000}{10}\) = 100 m/minute
Distance covered by C in 2 min- utes = 200 metre
Distance covered by B in 1 minute = 125 metre
Relative speed of A with respect to C = 100 metre
Time=\( \frac{200}{100}\)= 2 minutes
Relative speed of A with respect
ot B = 75 metre
Time=\( \frac{125}{75}\)= \( \frac{5}{3}\) minutes =1.6minutes

Q.29

Two cars are moving with speed v 1 , v 2 towards a crossing along two roads. If their distance from the crossing be 40 metres and 50 metres at an instant of time then they do not collide if their speed are such that

(1) v 1 : v 2 = 16 : 25

(2) v 1 : v 2 = 4 : 5

(3) v 1 : v 2 = 5 : 4

(4) v 1 : v 2 = 25 : 16

Ans .

(2) v 1 : v 2 = 4 : 5.

Explanation :

Q.30

The distance between place A and B is 999 km. An express train leaves place A at 6 am and runs at a speed of 55.5 km/hr. The train stops on the way for 1 hour 20 minutes. It reaches B at

(1) 1.20 am.

(2) 12 pm.

(3) 6 pm

(4) 11 pm

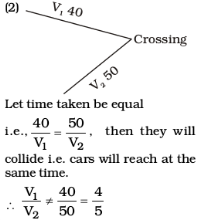
Ans .

(1) 1.20 am..

Explanation :

Time taken in covering 999km
\( \frac{999}{55.5}\)= 18 hours
Required time = 18 hours + 1
hour 20 minutes
= 19 hours 20 minutes
i.e. 1 : 20 am

Q.31

A speed of 45 km per hour is the same as

(1) 12.5 metre/seccond.

(2) 13 metre/seccond.

(3) 15 metre/seccond

(4) 12 metre/seccond

Ans .

(1) 12.5 metre/seccond.

Explanation :

Speed = 45 kmph
\( \frac{45*1000}{60*60}\)metre/second
\( \frac{45*5}{18}\)metre/second
= 12.5 metre/second

Q.32

If a distance of 50 m is covered in 1 minute, that 90 m in 2 min- utes and 130 m in 3 minutes find the distance covered in 15 min- utes.

(1) 610 m.

(2) 750 m.

(3) 1000 m

(4) 650 m

Ans .

(1) 610 m..

Explanation :

Distance covered in 2nd
minute = 90 – 50 = 40 metre
Distance covered in 3rd minute
= 130 – 90 = 40 metre
\ Required distance
= 50 + 40 × 14
= 50 + 560 = 610 metre

Q.33

A train leaves station A at 5 AM and reaches station B at 9 AM on the same day. Another train leaves station B at 7 AM and reaches station A at 10:30 AM on the same day. The time at which the two trains cross each other is :

(1) 8 : 26 AM

(2) 7: 36 AM

(3) 7: 56 AM

(4) 8 AM

Ans .

(3) 7: 56 AM

Explanation :

Here distance is constant.
Speed ∝ \( \frac{1}{Time}\)
Ratio of the speeds of A and B
\( \frac{\frac{7}{2}}{4}\)=7:8
A’s speed = 7x kmph (let)
B’s speed = 8x kmph
AB = 7x × 4 = 28x km.
Let both trains cross each other after t hours from 7 a.m. According to the question,
7x (t + 2) + 8x × t = 28x
7t + 14 + 8t = 28
15t = 28 – 14 = 14
t=\( \frac{14}{15}\)hours
\( \frac{14}{15}\)*60
=56 minutes.
Required time = 7 : 56 A.M.

Q.34

A plane can cover 6000 km in 8 hours. If the speed is increased by 250 kmph, then the time taken by the plane to cover 9000 km is

(1) 8 hours.

(2) 6 hours.

(3) 5 hours

(4) 9 hours

Ans .

(4) 9 hours

Explanation :

Speed of plane = \( \frac{Distance}{Time}\)
=\( \frac{6000}{8}\)= 750 kmph
New speed = (750 + 250) kmph
= 1000 kmph
Required time =\( \frac{9000}{1000}\)
= 9 hours

Q.35

A man travels 450 km to his home partly by train and partly by car. He takes 8 hours 40 minutes if he travels 240 km by train and rest by car. He takes 20 minutes more if he travels 180 km by train and the rest by car. The speed of the car in km/hr is

(1) 45.

(2) 50

(3) 60

(4) 48

Ans .

(1) 45

Explanation :

Let speed of train be x kmph.
Speed of car = y kmph.
Case I,
Time = \( \frac{Distance}{Speed}\)
\( \frac{240}{x}\) + \( \frac{210}{y}\)=8\( \frac{2}{3}\)
\( \frac{240}{x}\) + \( \frac{210}{y}\)=8\( \frac{26}{3}\)...(1)
Case II,
\( \frac{180}{x}\)+\( \frac{270}{y}\)=9....(2)
By equation (i) × 3 – (ii) × 4,
\( \frac{720}{x}\) +\( \frac{630}{y}\) -\( \frac{720}{x}\) -\( \frac{1080}{y}\)
= 26 – 36
=\( \frac{-450}{y}\)= –10
= –10
y = 45 kmph

Q.36

Two rifles are fired from the same place at a difference of 11 min. 45 seconds. But a man who is coming towards the same place in a train hears the second sound after 11 minutes. Find the speed of the train (Assuming speed of sound = 330 m/s).

(1) 72 km/h

(2) 36 km/h.

(3) 81 km/h

(4) 108 km/h.

Ans .

(3) 81 km/h.

Explanation :

Difference of time = 11 min- utes 45 seconds – 11 minutes = 45 seconds
Distance covered by sound in 45 seconds = Distance covered by train in 11 minutes
330 × 45 = 11 × 60 × Speed of train
Speed of train
\( \frac{330*45}{11*60}\)m/sec.
\( \frac{45}{2}\) \( \frac{18}{5}\)
=81 kmph

Q.37

A man can cover a certain dis- tance in 3 hours 36 minutes if he walks at the rate of 5 km/hr. If he covers the same distance on cycle at the rate of 24 km/hr, then the time taken by him in minutes is

(1) 40

(2) 45.

(3) 50

(4) 55.

Ans .

(2) 45

Explanation :

Distance covered in 3 hours
36 minutes i.e. 3\( \frac{36}{60}\)hours
=5\( \frac{18}{5}\)= 18 km.
Time taken at 24 kmph.
\( \frac{18}{24}\)hours
\( \frac{18}{24}\)*minutes
=45 minutes

Q.38

Due to inclement weather, an air plane reduced its speed by 300 km/hr, and reached the destina- tion of 1200 km late by 2hrs. Then the schedule duration of the flight was

(1) 1 hour

(2) 1.5 hours.

(3) 2 hours

(4) 2.5 hours

Ans .

(3) 2 hours

Explanation :

Let the origi nal speed of aeroplane be x kmph.
According to the question,
\( \frac{1200}{x-300}\)-\( \frac{1200}{x}\)=2
1200{\( \frac{x-x+300}{x(x-300)}\)}=2
x (x – 300) =\( \frac{1200*300}{2}\)
x (x – 300) = 600 × 300
x (x – 300) = 600 (600 – 300)
x = 600 kmph.
Scheduled duration of flight =\( \frac{1200}{600}\)= 2 hours

Q.39

A motor cycle gives an average of 45 km per litre. If the cost of petrol is Rs. 20 per litre, the amount required to complete a journey of 540 km is, (in Rupees)

(1) 120

(2) 360

(3) 20.

(4) 240.

Ans .

(4) 240.

Explanation :

Consumption of petrol in cov- ering 540 km=\( \frac{540}{45}\)= 12 litres
Required expenses
= Rs. (12 × 20)
= Rs. 240

Q.40

Ravi has a roadmap with a scale of 1.5 cm for 18 km. He drives on that road for 72 km. What would be his distance covered in that map?

(1) 4 cm.

(2) 6 cm

(3) 8 cm

(4) 7 cm.

Ans .

(2) 6 cm

Explanation :

18 km o 1.5 cm
1 km= \( \frac{1.5}{18}\)cm
72=\( \frac{1.5*72}{18}\)cm = 6 cm

Q.41

A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot at a speed of 4 km/ hour and partly on bicycle at a speed of 9 km/hour. The distance travelled on foot is :

(1) 14 km.

(2) 16 km.

(3) 20 km.

(4) 18 km.

Ans .

(2) 16 km.

Explanation :

Length of journey on foot = x km. (let).
\ Length of journey on cycle = (61 – x ) km.
According to the question,
Time = \( \frac{Distance}{Speed}\)
\( \frac{x}{4}\)+\( \frac{61-x}{9}\)=9
\( \frac{9x+244-4x}{36}\)=9
5x + 244 = 36 × 9 = 324
5x = 324 – 244 = 80
x=16 km

Q.42

A man travelled a distance of 61 km. in 9 hours, partly by walk- ing at the speed of 4 km./hr. and partly on bicycle at the speed of 9 km./hr. The distance covered by walking is

(1) 16 km.

(2) 12 km..

(3) 15 km.

(4) 17 km..

Ans .

(1) 16 km.

Explanation :

Let the distance covered on foot be x km.
Distance covered on cycle = (61 – x) km.
Time=\( \frac{Distance}{Speed}\)
\( \frac{x}{4}\)+\( \frac{61-x}{9}\)=9
\( \frac{x}{4}\)-\( \frac{x}{9}\)=9-\( \frac{61}{9}\)
\( \frac{5x}{36}\)=\( \frac{20}{9}\)
x=16 km

Q.43

Sound travels 330 metre in a second.When the sound follows the flash of lightning after 10 sec- onds the thunder cloud will be at a distance of :

(1) 1300 metre

(2) 2000 metre

(3) 3650 metre

(4) 3300 metre

Ans .

(4) 3300 metre

Explanation :

Distance = Speed × Time
= 330 × 10 = 3300 metre

Q.44

A man travels for 14 hours 40 minutes. He covers half of the journey by train at the rate of 60 km/hr and rest half by road at the rate of 50 km/hr. The dis- tance travelled by him is :

(1) 720 km

(2) 800 km

(3) 960 km

(4) 1000 km

Ans .

(2) 800 km.

Explanation :

Let total distance covered be 2x km.
Total time = 14 hours 40 min- utes
=14\( \frac{40}{60}\)hours=\( \frac{44}{3}\)hours
Time = \( \frac{Distance}{Speed}\)
According to the question,
\( \frac{x}{60}\)\)+\( \frac{x}{50}\)=\( \frac{44}{3}\)
\( \frac{11x}{300}\)=\( \frac{44}{3}\)
x=400
Total distance = 2x = 2 × 400 = 800 km

Q.45

Two donkeys are standing 400 metres apart. First donkey can run at a speed of 3 m/sec and the second can run at 2 m/sec. If two donkeys run towards each other after how much time (in seconds) will they bump into each other?

(1) 60

(2) 80.

(3) 400

(4) 40

Ans .

(2) 80

Explanation :

Distance between both don- keys = 400 metre.
Relative speed = (3 + 2) m./sec.
= 5 m./sec.
Required time
=\( \frac{Distance}{Relative Speed}\)
=\( \frac{400}{5}\)= 80 seconds

Q.46

A and B are 15 kms apart and when travelling towards each oth- er meet after half an hour where- as they meet two and a half hours later if they travel in the same direction. The faster of the two travels at the speed of

(1) 15 km./hr.

(2) 18 km./hr.

(3) 10 km./hr.

(4) 8 km./hr.

Ans .

(2) 18 km./hr.

Explanation :

Q.47

A man walking at 3 km/hour crosses a square field diagonally in 2 minutes. The area of the field (in square metre) is

(1) 3000

(2) 5000

(3) 6000

(4) 2500

Ans .

(2) 5000.

Explanation :

Speed of person = 3 kmph
=\( \frac{3000}{60}\)m./min
= 50 m./min.
Length of the diagonal of square field
= 50 × 2 = 100 metre
Required area = \( \frac{1}{2}\)*( 100 ) ²
= 5000 sq. metre

TEST YOURSELF

Q.1

Express speed of 36 km per hr. in metres per second.

(1) 10 m/sec.

(2) 8 m/sec.

(3) 12 m/sec.

(4) 18m/sec.

Ans .

(1) 10 m/sec.

Explanation :

36 km/hr.
36*\( \frac{5}{18}\)
= 10 m/sec.

Q.2

Express speed of 60 metres per sec. in km per hour.

(1) 232 kmph

(2) 216 kmph

(3) 116 kmph

(4) 118 kmph

Ans .

(2) 216 kmph

Explanation :

60 metres per sec.
60* \( \frac{18}{5}\)
= 216 km per hr.

Q.3

A man covers 20 kms in 2 hours. Find the distance covered by him in 5\( \frac{1}{2}\) hr.

(1) 50 km

(2) 65 km

(3) 55 km

(4) 45 km

Ans .

(3) 55 km.

Explanation :

Distance = 20 kms
Time = 2 hours
Speed = \( \frac{Distance}{Time}\)
\( \frac{20}{2}\)=10 km per hr..
Now, we have, Speed = 10 km per hr
Time=\( \frac{11}{2}\) hour
Distance = Speed × Time
10*\( \frac{11}{2}\)=55 km

Q.4

A car runs at 60 km per hr. A man runs at one-third the speed of the car and reaches office from his house in 15 minutes. How far is his office from his house?

(1) 7 km

(2) 5.5 km

(3) 6 km

(4) 5 km

Ans .

(4) 5 km

Explanation :

Man’s speed =\( \frac{1}{3}\)of the speed of car=\( \frac{1}{3}\)* 60= 20 km per hr..
Time taken to reach office= 15 minutes =\( \frac{15}{60}\)=\( \frac{1}{4}\) hour
Distance between his house and office = Speed × Time
20*\( \frac{1}{4}\)= 5 km.

Q.5

Walking at a speed of 6 km per hour, a man takes 5 hours to complete his journey. How much time will he need to complete the same journey at the rate of 8 km per hr.?

(1) 3 hours

(2) 37.5 hour

(3) 4 hours

(4) 2 hours

Ans .

(2) 37.5 hour

Explanation :

Speed = 6 km/hr
Time taken = 5 hours
\ Distance covered
= 6 × 5 = 30 kms
\ Time required to cover 30 kms
at the speed of 8 km/hr.
\( \frac{Distance}{Speed}\)=\( \frac{30}{8}\)=3\( \frac{3}{4}\)=37.5 hour

Q.6

A person covers 10 kms at 4 km per hr. and then further 21 kms at 6 km per hr. Find his average speed for whole journey

(1) 5 kmph

(2) 5.16 kmph

(3) 4 kmph

(4) 3 kmph

Ans .

(2) 5.16 kmph

Explanation :

Case I.
Distance = 10 kms
Speed = 4 km/hr.
Time taken (t₁) =\( \frac{10}{4}\)=\( \frac{5}{2}\)hr.
Case II.
Distance = 21 kms
Speed = 6 km/hr
. Time taken (t₂) =\( \frac{21}{6}\)=\( \frac{7}{2}\)hr.
Total time taken =\( \frac{5}{2}\)+\( \frac{7}{2}\)= 6 hrs.
Total distance covered
= 10 + 21 = 31 kms
\ Average Speed
\( \frac{Total distance}{Total time}\)=\( \frac{31}{6}\)=5\( \frac{1}{6}\)=5.16 km per hr..

Q.7

P and Q are two cities. A boy trav- els on cycle from P to Q at a speed of 20 km per hr. and re- turns at the rate of 10 km per hr. Find his average speed for the whole journey.

(1) 14.5 kmph

(2) 13.4 kmph

(3) 12.5 kmph

(4) 25 kmph

Ans .

(2) 13.4 kmph.

Explanation :

Let the speed between P and Q be x km.
Then time taken to cover x km.
P to Q =\( \frac{x}{20}\)
Time taken to cover x km from
Q to P at 10 km per hr. P to Q=\( \frac{x}{10}\)
Total distance covered
= x + x = 2x km.
Time taken to cover 2x km
\( \frac{x}{20}\) + \( \frac{x}{10}\)=\( \frac{3x}{20}\)
Average Speed
\( \frac{2x}{\frac{3x}{20}}\)=\( \frac{2x*20}{3x}\)=\( \frac{40}{3}\)=13.4 km per hr..

Q.8

A man walked a certain distance. One-third he walked at 5 km per hr. Another one-third he walked at 10 km per hr. and the rest at 15 km per hr. Find his average speed.

(1) 3 kmph

(2) 8.1 kmph

(3) 6 kmph

(4) 2 kmph

Ans .

(2) 8.1 kmph

Explanation :

Here, the man covers equal distance at different speeds. Us- ing the formula, the Average Speed is given by
\( \frac{3}{\frac{1}{5}+\frac{1}{10}+\frac{1}{15}}\)=\( \frac{90}{11}\)= 8.1 km per hour..

Q.9

An aeroplane travels a distance in the form of a square with the speed of 400 km per hr, 600 km per hr, 800 km per hr. and 1200 km per hr respectively. Find the average speed for the whole dis- tance along the four sides of the square.

(1) 640 kmph

(2) 620 kmph

(3) 630 kmph

(4) 650 kmph

Ans .

(1) 640 kmph.

Explanation :

As distance is covered along four sides (equal) of a square at different speeds, the average speed of the aeroplane
\( \frac{4}{\frac{1}{400}+\frac{1}{600}+\frac{1}{800}+\frac{1}{1200}}\) \( \frac{48000}{75}\)= 640 km per hr..

Q.10

A man covers one-third of his journey at 30 km per hr. and the remaining two-third at 45 km per hr. If the total journey is of 150 kms, what is his average speed for the whole journey?

(1) 38 kmph

(2) 38.57 kmph

(3) 36 kmph

(4) 32 kmph

Ans .

(2) 38.57 kmph.

Explanation :

Length of journey = 150 kms
\( \frac{1}{3}\)rd of journey =\( \frac{150}{3}\)= 50 kms
Remaining \( \frac{2}{3}\) journey = 150 – 50 = 100 kms
Time taken in \( \frac{1}{3}\)rd journey at 30 km per hr. t₁=\( \frac{5}{3}\) hr
Time taken in \( \frac{2}{3}\) rd journey at 45 km per hr. t₂=\( \frac{20}{9}\) hr
Total time taken in whole jour- ney = t₁ + t₂
\( \frac{5}{3}\)+\( \frac{20}{9}\)=\( \frac{35}{9}\)hr
Average Speed \( \frac{150}{\frac{35}{9}}\)=\( \frac{270}{7}\)=38.57 km per hr..

Q.11

When a person covers the dis- tance between his house and of- fice at 50 km per hr. he is late by 20 minutes. But when he trav- els at 60 km per hr. he reaches 10 minutes early. What is the distance between his office and his house?

(1) 140 km.

(2) 160 km.

(3) 150 km.

(4) 120 km.

Ans .

(3) 150 km..

Explanation :

Let time taken to reach of fice at 50 kmph be x hrs
Then time taken to reach office at 60 kmph =x+ \( \frac{30}{60}\)hrs
As, distance covered is same, x* 50 =60 {x+\( \frac{30}{60}\)}
50x = 60x + 30
x = 3 hrs
Hence, distance = 3 × 50
= 150 km

Q.12

A boy walks from his house at 4 km per hr. and reaches his school 9 minutes late. If his speed had been 5 km per hr. he would have reached his school 6 minutes earlier. How far his school from house?

(1) 6.5 km.

(2) 5.5 km.

(3) 6 km.

(4) 5 km.

Ans .

(4) 5 km.

Explanation :

Let time taken to reach school at 4 kmph be x hrs.
Then time taken to reach school at 5 kmph =x+ \( \frac{15}{60}\)hr
Since, distance is equal.
4x= 5{x+\( \frac{15}{60}\)}
x=\( \frac{5}{4}\)hr.
Hence, distance between school & house =4*\( \frac{5}{4}\)km = 5 km

Q.13

A car travels a distance of 300 kms at uniform speed. If the speed of the car is 5 km per hr more it takes two hours less to cover the same distance. Find the original speed of the car.

(1) 25 kmph

(2) 20 kmph

(3) 24 kmph

(4) 28 kmph

Ans .

(1) 25 kmph.

Explanation :

Let the original speed of the car = x km per hr.
When it is increased by 5 km per hr, the speed = x + 5 km per hr.
As per the given information in the question,
\( \frac{300}{x}\)-\( \frac{300}{x+5}\)=2
\( \frac{1500}{x+5x}\)=2
x 2 + 5x = 750
x 2 + 5x – 750 = 0
x 2 + 30x – 25x – 750 = 0
x (x + 30) – 25 (x + 30) = 0
(x + 30) (x – 25) = 0
x = – 30 or 25
The negative value of speed is inadmissible.
Hence, the required speed = 25 km per hr

Q.14

A car can finish a certain jour- ney in 10 hours at a speed of 48 km per hr. In order to cover the same distance in 8 hours, how much the speed be increased by ?

(1) 10 kmph

(2) 12 kmph

(3) 14 kmph

(4) 15 kmph

Ans .

(2) 12 kmph.

Explanation :

Time = 10 hours,
Speed = 48 km per hr.
Distance = Speed × Time
= 48 × 10 = 480 km
Now, this distance of 480 kms is to be covered in 8 hours. Hence, the required Speed
\( \frac{Distance}{New time}\)=\( \frac{480}{8}\)
= 60 km per hr.Increase in speed = 60 – 48 = 12 km per hr.

Q.15

If a boy walks from his house to school at the rate of 4 km per hr, he reaches the school 10 min- utes earlier than the scheduled time. However if he walks at the rate of 3 km per hr, he reaches 10 minutes late. Find the dis- tance of his school from his house.

(1) 3.5 km

(2) 3 km

(3) 4 km

(4) 4.5 km

Ans .

(3) 4 km

Explanation :

Let the distance be x kms.
Time taken at 4 km per hr. t ₁=\( \frac{x}{4}\)hr
Time taken at 3 km per hr. t ₂=\( \frac{x}{3}\)hr
Difference in timings = 10 + 10 = 20 minutes
or \( \frac{20}{60}\)=\( \frac{1}{3}\)hour
\( \frac{x}{3}\)-\( \frac{x}{4}\)=\( \frac{1}{3}\)
\( \frac{x}{12}\)=\( \frac{1}{3}\)
x = 4 km.
Hence the required distance = 4 kms.

Q.16

A man has to reach a place 40 kms away. He walks at the rate of 4 km per hr. for the first 16 kms and then he hires a rick- shaw for the rest of the journey. However if he had travelled by the rickshaw for the first 16 kms and the remaining distance on foot at 4 km per hr, he would have taken an hour longer to complete the journey. Find the speed of rickshaw.

(1) 6.5 kmph

(2) 7.5 kmph

(3) 6 kmph

(4) 8 kmph

Ans .

(4) 8 kmph

Explanation :

Let the speed of Rickshaw be 'x ' .
Then, time taken to cover 16 km on foot and 24 km on Rikshaw =\( \frac{16}{4}\)+\( \frac{24}{x}\)hr
and time taken to travel 24 km
on foot & 16 km on Rikshaw=\( \frac{16}{x}\)+\( \frac{24}{4}\)hr
According to question,
\( \frac{16}{4}\)+\( \frac{24}{x}\)+1=\( \frac{16}{x}\)+\( \frac{24}{4}\)
\( \frac{24-16}{x}\)=1
x = 8 km/hr

Q.17

Walking \( \frac{3}{4}\)of my usual speed, a late is marked on my cards by 10 minutes. Find my usual time.

(1) 30 minutes

(2) 35 minutes

(3) 32 minutes

(4) 36 minutes

Ans .

(1) 30 minutes

Explanation :

Since I walk at \( \frac{3}{4}\)of my usual speed the time taken is \( \frac{4}{3}\) of my usual time.
\( \frac{4}{3}\)of usual time
= Usual time + Time I reach late
\( \frac{1}{3}\)of usual time
= 10 minutes
Usual time = 10 × 3 = 30 minutes.

Q.18

By walking \( \frac{5}{3}\)of usual speed a student reaches school 20 min- utes earlier. Find his usual time.

(1) 45 minutes

(2) 50 minutes

(3) 60 minutes

(4) None of these

Ans .

(2) 50 minutes

Explanation :

\( \frac{5}{3}\)of usual speed means\( \frac{3}{5}\) of usual time as he reaches earlier.
\( \frac{3}{5}\)usual time + 20 minutes=Usual time
20 minutes= 1-\( \frac{3}{5}\)usual time
=\( \frac{2}{5}\) usual time
Usual time \( \frac{20*5}{2}\)=50 minutes

Q.19

Walking at \( \frac{3}{4}\)of his usual speed a man is late by 2\( \frac{1}{2}\) usual time would have been what?

(1) 7 hours

(2) 7.5 hours

(3) 8 hours

(4) 8.5 hours

Ans .

(2) 7.5 hours

Explanation :

New speed is\( \frac{3}{4}\)of the usual speed
New time taken =\( \frac{4}{3}\)of the usual time
\( \frac{4}{3}\)of the usual time – Usual time =\( \frac{5}{2}\)
\( \frac{1}{3}\)of the usual time =\( \frac{5}{2}\)
Usual time =\( \frac{5}{2}\)*3
=\( \frac{15}{2}\)hours or 7.5 hrs

Q.20

Two men A and B walk from X to Y a distance of 42 kms at 5 km and 7 km an hour respectively. B reaches Y and returns imme- diately and meets A at R. Find the distance from X to R.

(1) 32 km

(2) 30 km

(3) 35 km

(4) 40 km

Ans .

(3) 35 km.

Explanation :

When B meets A at R,
by then B has walked a distance (XY + YR) and A,the distance XR.
That is both of them have togeth- er walked twice the distance from X to Y, i.e., 42 kms.

Q.21

Two men A and B start walking simultaneously from P to Q, a distance of 21 kms, at the speed of 3 km and 4 km an hour re- spectively. B reaches Q, returns immediately and meets A at R. Find the distance from P to R.

(1) 22 km

(2) 20 km

(3) 16 km

(4) 18 km

Ans .

(4) 18 km

Explanation :

Q.22

Ram travelled one-third of a jour- ney with a speed of 10 km per hr, the next one-third with a speed of 9 km per hr. and the rest at a speed of 8 km per hr. If he had travelled half the journey at speed of 10 km per hr. and the other half with a speed of 8 km per hr, he would have been 1 minute longer on the way. What distance did he travel?

(1) 36 km

(2) 32 km

(3) 35 km

(4) 40 km

Ans .

(1) 36 km

Explanation :

Let the total distance travelled be x kms.
Case I : Speed for the first one-third distance \( \frac{x}{3}\)kms =10 km per hr.
Time taken =\( \frac{x}{30}\)hours
Similarly, time taken for the next one-third distance=\( \frac{x}{27}\)hour
and time taken for the last one third distance =\( \frac{x}{24}\)hour
Total time taken to cover x kms \( \frac{x}{30}\)+\( \frac{x}{27}\)+\( \frac{x}{24}\)hour Case II :
Time taken for one-half distance at the speed of 10 km per hr. \( \frac{x}{20}\)hr
and time taken for remaining \( \frac{1}{2}\) of distance \( \frac{x}{16}\)hrs. at 8 km per hr.
Total time taken \( \frac{x}{20}\)+\( \frac{x}{16}\)hr
Time taken in (Case II – Case I)
1 minute=\( \frac{1}{60}\)hr
According to the question
\( \frac{x}{20}\)+\( \frac{x}{16}\)-\( \frac{x}{30}\)+\( \frac{x}{27}\)+\( \frac{x}{24}\)hour=\( \frac{1}{60}\)
\( \frac{x}{2160}\)=\( \frac{1}{60}\)
x=36 km
Hence the required distance = 36 km.

Q.23

A man walks a distance of 35 kms. He walks for some time at 4 km per hour and for some time at 5 km per hr. If he walks at 5 km per hr. instead of 4 km per hr. and 4 km per hr. instead of 5 km per hr, he will walk 2 kms more in the same span of time. Find his total time of total journey.

(1) 8.5 hours

(2) 7.5 hours

(3) 8 hours

(4) 7 hours

Ans .

(3) 8 hours

Explanation :

hours at 4 km per hr. and y hours at 5 km per hr. and cov- ers a distance of 35 kms.
Distance = 4x + 5y = 35 ...(i)
Now, he walks at 5 km per hr.
for x hours and at 4 km per hr.
for y hours and covers a distance (35 + 2) = 37 kms
Distance = 5x + 4y = 37...(ii)
By 5 × (i) – 4 × (ii) we have
20x + 25y = 175
20x + 16y = 148
By solving these equations, y=3
Putting the value of (y) in equa- tion (i), we have
4x + 5 × 3 = 35
4x = 35 – 15 = 20
x = 5
Total time taken
= x + y = 5 + 3 = 8 hours.

Q.24

A man travels 400 kms in 4 hours partly by air and partly by train. If he had travelled all the way by air, he would have saved\( \frac{4}{5}\) of the time he was in train and would have arrived his des- tination 2 hours early. Find the distance he travelled by train.

(1) 95 km.

(2) 85 km.

(3) 90 km.

(4) 100 km.

Ans .

(4) 100 km.

Explanation :

Obviously,\( \frac{4}{5}\)of total time in train = 2 hour
Total time in train=\( \frac{5}{4}\)*2=\( \frac{5}{2}\)hr
Total time to cover 400 km is 4 hours
\ Time spent in travelling by air= 4-\( \frac{5}{2}\)=\( \frac{3}{2}\)hr
If 400 kms is travelled by air, then time taken = 2 hours
\ In 2 hours, distance covered by air = 400 kms
In \( \frac{3}{2}\)hr distance covered \( \frac{400}{2}\)*\( \frac{3}{2}\) = 300 kms
Distance covered by the train = 400 – 300 = 100 kms.

Q.25

On increasing the speed of a train at the rate of 10 km per hr, 30 minutes is saved in a journey of 100 kms. Find the initial speed of train.

(1) 40 kmph

(2) 45 kmph

(3) 42 kmph

(4) 44 kmph

Ans .

(1) 40 kmph

Explanation :

Let the original speed be x km/hr then, increased speed
= (x + 10) km/hr
According to question,
\( \frac{100}{x}\)-\( \frac{100}{x+10}\)=\( \frac{30}{60}\)
100[\( \frac{1}{x}\)-\( \frac{1}{x+10}\)]=\( \frac{1}{2}\)
10 × 200 = x (x + 10)
x 2 + 10x – 2000 = 0
x 2 + 50x – 40x – 2000 = 0
x (x + 50) – 40 (x + 50) = 0
x = – 50, 40
Speed can’t be negative.
Hence, Original speed = 40 kmph

Q.26

Ravi can walk a certain distance in 40 days when he rests 9 hours a day. How long will he take to walk twice the distance, twice as fast and rest twice as long each day?

(1) 80 days

(2) 100 days

(3) 90 days

(4) 95 days

Ans .

(2) 100 days.

Explanation :

Working hours per day= 24 – 9 = 15 hrs.
Total working hours for 40 days = 15 × 40 = 600 hrs.
On doubling the distance, the time required becomes twice but on walking twice as fast, the time required gets halved. Therefore, the two together cancel each other with respect to time re- quired. Increasing rest to twice reduces walking hours per day to 24 – (2 × 9) = 6 hrs.
\ Total number of days required to cover twice the distance, at twice speed with twice the rest. \( \frac{600}{6}\)=100 days

Q.27

A monkey climbing up a greased pole ascends 12 metres and slips down 5 metres in alternate minutes. If the pole is 63 metres high, how long will it take him to reach the top?

(1) 18 minutes

(2) 16 minutes

(3)16.58 minutes

(4) 25 minutes

Ans .

(3)16.58 minutes.

Explanation :

In 1 minute the monkey climbs 12 metres but then he takes 1 minute to slip down 5 metres. So, at the end of 2 min- utes the net ascending of the monkey is 12 – 5 = 7 metres.
So, to cover 63 metres the above process is repeated \( \frac{63}{7}\)=9 times. Obviously, in 9 such hap- penings the monkey will slip 8 times, because on 9th time, it will climb to the top.
Thus, in climbing 8 times and slipping 8 times, he covers 8 × 7 = 56 metres.
Time taken to cover 56 metres \( \frac{56*2}{7}\)= 16 minutes = 16 minutes
\( \frac{7}{12}\)minutes
Total time taken = 16 + \( \frac{7}{12}\) =16.58 minutes

Q.28

A hare sees a dog 100 metres away from her and scuds off in the opposite direction at a speed of 12 km per hr. A minute later the dog perceives her and chases her at a speed of 16 km per hr. How soon will the dog overtake the hare and at what distance from the spot when the hare took flight?

(1) 900 metres

(2) 950 metres

(3) 1000 metres

(4) 1100 metres

Ans .

(4) 1100 metres

Explanation :

Q.29

A hare, pursued by a grey hound is 50 of her own leaps before him. While the hare takes 4 leaps, the grey hound takes 3 leaps. In one leap, the hare goes 1.75 metres and the grey hound 2.75 metres. In how many leaps, will the grey hound overtake the hare?

(1) 210 leaps

(2) 220 leaps

(3) 230 leaps

(4) 250 leaps

Ans .

(1) 210 leaps

Explanation :

Grey hound and hare make 3 leaps and 4 leaps respective- ly.
This happens at the same time. The hare goes 1.75 metres in 1 leap.
Distance covered by hare in 4 leaps = 4 × 1.75 = 7 metres The grey hound goes 2.75 metres in one leap
Distance covered by it in 3 leaps = 3 × 2.75 = 8.25 metres
Distance gained by grey hound in 3 leaps=(825-7) = 1.25 metres
Distance covered by hare in 50 leaps = 50 × 1.75 metres = 87.5 metres
Now, 1.25 metres is gained by grey hound in 3 leaps 87.5 metres is gained in \( \frac{3}{1.25}\)*87.5
= 210 leaps.

Q.30

In a flight of 600 kms, an air- craft was slowed down due to bad weather. Its average speed for the trip was reduced by 200 km per hr. and the time of flight increased by 30 minutes. Find the duration of flight.

(1) 1.2 hours

(2) 1 hour

(3) 1.5 hours

(4) 2 hours

Ans .

(2) 1 hour.

Explanation :

Let the original speed be x kmph then,
new speed = (x – 200) kmph
According to question,
Time taken with new speed – time taken with original speed =30 min. i.e \( \frac{1}{2}\)
\( \frac{600}{x-200}\)-\( \frac{600}{x}\)=\( \frac{1}{2}\)
\( \frac{x-x+200}{x(x-200)}\)=\( \frac{1}{1200}\)
24000 = x (x – 200)
x 2 – 200x – 24000 = 0
x 2 – 600x + 400x – 24000 = 0
x (x – 600) + 400 (x – 600) = 0
(x – 600) (x + 400) = 0
x = 600, – 400
Speed cannot be negative Hence, original speed = 600 kmph and duration of flight =1 hour

Q.31

Two trains leave a railway sta- tion at the same time. The first train travels due west and the second train due north. The first train travels 5 km per hr. faster than the second train. If after two hours they are 50 km apart, find the average speed of faster train.

(1) 18 kmph

(2) 15 kmph

(3) 20 kmph

(4) 25 kmph

Ans .

(2) 15 kmph.

Explanation :

Let the speed of the second train be x km per hr. Then the speed of the first train is x + 5 km per hr.

Let O be the position of the rail- way station from which the two trains leave. Distance travelled by the first train in 2 hours = OA = 2 (x + 5) km.
Distance travelled by the 2nd train in 2 hours= OB = 2x km.
By Pythagoras theorem, AB ² = OA²+ OB²
50 ² = [2 (x + 5)]² + [2x] ²
2500 = 4 (x + 5) ²+ 4x ²
2500 = 4 (x ² + 10x + 25) + 4x ²

8x² + 40x – 2400 = 0
x ² + 5x – 300 = 0
x ² + 20x – 15x – 300 = 0
x (x + 20) – 15 (x + 20) = 0
(x – 15) (x + 20) = 0
x = 15, – 20
But x cannot be negative
x = 15
The speed of the second train is 15 km per hr. and the speed of the first train is 20 km per hr.

Q.32

A carriage driving in a fog passed a man who was walking at the rate of 6 km per hr. in the same direction. He could see the car- riage for 4 minutes and it was visible to him up to a distance of 200 metres. Find the speed of the carriage.

(1) 8.75 kmph

(2) 8.5 kmph

(3) 8 kmph

(4) 9 kmph

Ans .

(4) 9 kmph

Explanation :

The distance covered by man in 4 minutes \( \frac{6*1000*4}{60}\)= 400 metres
The distance covered by carriage in 4 minutes = 200 + 400 = 600 metres
Speed of carriage Speed of carriage=\( \frac{600}{4}\)*\( \frac{60}{1000}\) = 9 km per hr.

Q.33

Two bullets were fired at a place at an interval of 12 minutes. A person approaching the firing point in his car hears the two sounds at an interval of 11 min- utes 40 seconds. The speed of sound is 330 metres per second. What is the approximate speed of the car?

(1) 34 kmph

(2) 32 kmph

(3) 36 kmph

(4) 38 kmph

Ans .

(1) 34 kmph.

Explanation :

If the car were not moving, the person would have heard the two sounds at an interval of 12 minutes.
Therefore, the distance travelled by car in 11 minutes 40 seconds is equal to the dis- tance that could have been cov- ered by sound in 12 min – 11 min. 40 seconds = 20 seconds. Distance covered by sound in 20 seconds
= 330 × 20 = 6600 m
In 11 min 40 seconds or 700 seconds the car travels 6600 m.
In 1 second the car will travel
\( \frac{6600}{700}\)=\( \frac{66}{7}\)metre
Speed of the car = \( \frac{66}{7}\)metre per second
\( \frac{66}{7}\)*\( \frac{18}{5}\)
=34 kmph

Q.34

A and B start simultaneously at 5 km per hr. and 4 km per hr. from P and Q, 180 kms apart, towards Q and P respectively. They cross each other at M and after reaching Q and P turn back immediately and meet again at N. Find the distance MN.

(1) 45 km

(2) 40 km

(3) 35km

(4) 42 km

Ans .

(2) 40 km.

Explanation :

When A and B cross each other at M for the first time, they have together covered the whole dis- tance PQ = 180 km.
When they meet again at N, they have together covered total dis- tance equal to 3 times of PQ = 3 × 180 = 540 km.
PM=\( \frac{5}{5+4}\)*180= 100 km
QP + PN =\( \frac{4}{5+4}\)*540
= 240 km
or PN = 240 – QP = 240 – 180 = 60 km.
Then, MN = PM – PN = 100 – 60 = 40 km.

Q.35

A car driving in the morning fog passes a man walking at 4 km per hr. in the same direction. The man can see the car for 3 min- utes and visibility is upto a dis- tance of 130 metres. Find the speed of the car.

(1) 7.5 kmph

(2) 6.6 kmph

(3) 6 kmph

(4) 7 kmph

Ans .

(2) 6.6 kmph

Explanation :

Distance covered by man in 3 minutes
[\( \frac{4*1000}{60}\)]\( \frac{m}{minutes}\)*3 minutes =200 metres
Total distance covered by the car in 3 min.
= (200 + 130) m = 330 metres
Speed of the car \( \frac{330}{3}\) = 110 m per minutes
\( \frac{\frac{110}{1000}}{\frac{1}{60}}\)=6.6 kmph

Q.36

Ram starts his journey from Bombay to Pune and simulta- neously Mohan starts from Pune to Bombay. After crossing each other they finish their remaining journey in 6 \( \frac{1}{4}\)and 4 hours respectively. What is Mohan’s speed if Ram’s speed is 20 km per hr. ?

(1) 28 kmph

(2) 24 kmph

(3) 25 kmph

(4) 30 kmph

Ans .

(3) 25 kmph

Explanation :

Suppose that Ram and Mohan meet at A. Let Ram’s speed be x km per hr.
and Mohan’s speed be y km per hr. Then AP=\( \frac{25}{4}\)x
km and AB = 4y km.
Now, time taken by Ram in going from B to A =\( \frac{4y}{x}\)
and the time taken by Mohan in going from P to A =\( \frac{25x}{4y}\)
Obviously time taken is equal
\( \frac{4y}{x}\)=\( \frac{25x}{4y}\)
16y 2 = 25x 2
\( \frac{y}{x}\)=\( \frac{5}{4}\)
y=\( \frac{5}{4}\)x
Here, x = 20 km per hr.
y = Mohan’s speed
\( \frac{5}{4}\)*20=25 km per hr..

Q.37

A train meets with an accident after travelling 30 kms, after which it moves with \( \frac{4}{5}\)of its original speed and arrives at the destination 45 minutes late. Had the accident happened 18 kms further on, it would have been 9 minutes before. Find the dis- tance of journey and original speed of the train.

(1) 120 km ; 25 kmph

(2) 125 km ; 25 kmph

(3) 130 km ; 30 kmph

(4) 120 km ; 30 kmph

Ans .

(4) 120 km ; 30 kmph

Explanation :

Let the original speed be x and distance be y
Case I.
Time taken by train to travel 30 km= \( \frac{30}{x}\)
Time taken by train after acci- dent=\( \frac{y-30}{\frac{4}{5}x}\)
Total time taken =\( \frac{30}{x}\)+\( \frac{y-30}{\frac{4}{5}x}\)
Case II :
Time taken by train to travel 48 km =\( \frac{48}{x}\)
Time taken by train after accident =\( \frac{y-48}{\frac{4}{5}x}\)
Total time taken =\( \frac{48}{x}\)+\( \frac{y-48}{\frac{4}{5}x}\)
According to question,
\( \frac{30}{x}\)+\( \frac{y-30}{\frac{4}{5}x}\) - \( \frac{48}{x}\)+\( \frac{y-48}{\frac{4}{5}x}\)=\( \frac{9}{60}\)
\( \frac{90-72}{4x}\)=\( \frac{9}{60}\)
x=30
Hence, original speed = 30 kmph
Also \( \frac{30}{x}\)+\( \frac{y-30}{\frac{4}{5}x}\) =\( \frac{y}{x}\)=\( \frac{45}{60}\)
3x – y = –30
3(30) – y = –30
y = 120 km
i.e. Distance = 120 km

Q.38

A train met with an accident 3 hours after starting, which de- tains it for one hour, after which it proceeds at 75% of its original speed. It arrives at the destina- tion 4 hours late. Had the acci- dent taken place 150 km further along the railway line, the train would have arrived only 3\( \frac{1}{2}\)hours late. Find the length of the trip and the original speed of the train.

(1) 1100 km ; 100 kmph

(2) 1200 km ; 100 kmph

(3) 1200 km ; 90 kmph

(4) 1600 km ; 90 kmph

Ans .

(2) 1200 km ; 100 kmph

Explanation :

Let A be the starting point, B the terminus. C and D are points where accidents take place.

0.75=\( \frac{3}{4}\)
By travelling at \( \frac{3}{4}\) of its original speed,
the train would take \( \frac{4}{3}\)of its usual time i.e.,\( \frac{1}{3}\)more of the usual time.
\( \frac{1}{3}\)of the usual time taken to travel the distance CB. = 4 – 1 = 3 hrs
and \( \frac{1}{3}\)of the usual time taken to travel the distance
DB=3\( \frac{1}{2}\)-1=2\( \frac{1}{2}\)
Subtracting equation (ii) from (i)
we can write,\( \frac{1}{3}\)of the usual time taken to travel the distance
CD=3-2\( \frac{1}{2}\)=\( \frac{1}{2}\)hr
Usual time taken to travel CD=\( \frac{\frac{1}{2}}{\frac{1}{2}}\)=\( \frac{3}{2}\)
Usual sp eed of the train =\( \frac{150}{\frac{3}{2}}\)= 100 km per hr.
Usual time taken to travel CB =\( \frac{3}{\frac{1}{3}}\)= 9 hrs.
Total time = 3 + 9 = 12 hrs.
Length of the trip = 12 × 100 = 1200 km.

Q.39

A train after travelling 100 kms from P meets with an accident and then proceeds at \( \frac{3}{4}\) of its original speed and arrives at the terminus Q 90 minutes late. Had the accident occurred 60 kms further on, it would have reached 15 minutes sooner. Find the origi- nal speed of the train and the distance PQ.

(1) 65 kmph; 480 km

(2) 75 kmph; 450 km

(3) 80 kmph; 460 km

(4) 85 kmph; 460 km

Ans .

(3) 80 kmph; 460 km

Explanation :

Let P be the starting point, Q the terminus, M and N the places where accidents occur.
At \( \frac{3}{4}\)th of the original speed,
the train will take \( \frac{4}{3}\)of its usual time to cover the same distance
i.e.,\( \frac{1}{3}\)rd more than the usual time.
\( \frac{1}{3}\)rd of the usual time to travel a distance of 60 kms between MN = 15 min.
Usual time to travel 60 kms
= 15 × 3 = 45 min. =\( \frac{3}{4}\)hr
Usual speed of the train per hour = 60 *\( \frac{4}{3}\)= 80 km per hr..

Usual time taken to travel MQ=90 × 3
= 270 minor \( \frac{9}{2}\)
The distance MQ 80*\( \frac{9}{2}\)= 360 km.
Therefore, the total distance PQ
= PM + MQ
= 100 + 360 = 460 kms.

Q.40

Two trains A and B are 110 km apart on a straight line. One train starts from A at 7 a.m. and travels towards B at 20 km per hr. Another train starts from B at 8 am. and travels towards A at a speed of 25 km per hr. At what time will they meet?

(1) 10 : 15 a.m.

(2) 09 : 50 a.m.

(3) 09 : 30 a.m.

(4) 10 : 00 a.m

Ans .

(4) 10 : 00 a.m.

Explanation :

Let they meet x hrs after 7 am.
Di stance covered by A i n x hours = 20x km
Distance covered by B in (x –1) hr.
= 25 (x – 1) km
20x + 25 (x – 1) = 110
20x + 25x – 25 = 110
45x = 110 + 25 = 135
x = 3
Trains meet at 10 a.m.

Q.41

Two boys begin together to write out a booklet containing 817 lines. The first boy starts with the first line, writing at the rate of 200 lines an hour and the second boy starts with the last lines then writes line 816 and so on. Backward proceeding at the rate of 150 lines an hour. At what line will they meet?

(1) 467 th line

(2) 468 th line

(3) 470 th line

(4) 475 th line

Ans .

(1) 467 th line.

Explanation :

Writing ratio = 200 : 150 = 4 : 3 In a given time first boy will be writing the line number \( \frac{4}{7}\)*817 \( \frac{3268}{7}\)th line
=466\( \frac{6}{7}\)
Hence, both of them shall meet on 467th line

Q.42

Two men set out the same time to walk towards each o ther from two points A and B, 72 km apart. The first man walks at the rate of 4 km per hr. The sec- ond man walks 2 km in the first2 \( \frac{1}{2}\) km in the second hour, 3 km in the third hour and so on. Find the time after which the two men will meet.

(1) 8 hours

(2) 9 hours

(3) 8.5 hours

(4) 9.5 hours

Ans .

(2) 9 hours

Explanation :

Let the two men meet after t hours.

Distance covered by the first man starting from A = 4 t km.
Distance covered by the second man starting from B
= 2 + 2 . 5 + 3 + ..... +[2+\( \frac{t-1}{2}\)]
This is an arithmetic series of t terms with \( \frac{1}{2}\)as common difference
By applying formula S=\( \frac{n}{2}\)[2 a + (n – 1) d]
Where, n = no. of terms
a = first term
d = common difference
We have its sum =\( \frac{t}{2}\)[2*2+(t-1)*\( \frac{1}{2}\)]
2t+\( \frac{t²-t}{4}\)
Total distance covered by two men =4 t + 2 t +\( \frac{t²-t}{4}\) =72
or 24t+t²-t=288
or t 2 – 9t + 32t – 288 = 0
or t (t–9) + 32 (t – 9) = 0
or (t – 9) (t + 32) = 0
Either t – 9 = 0
t = 9,-32
Time cannot be negative. Hence, the two men will meet after 9 hrs.

Q.43

A man is standing on a railway bridge which is 50 metres long. He finds that a train crosses the bridge in 4\( \frac{1}{2}\)seconds but himself in 2 seconds. Find the length of the train and its speed.

(1) 60 m ; 20 m/sec

(2) 40 m ; 20 kmph

(3) 40 m ; 20 m/sec

(4) 40 m ; 25 m/sec

Ans .

(3) 40 m ; 20 m/sec

Explanation :

Let the length of the train be x metres
Then, the time taken by the train to cover (x + 50) metres is 4\( \frac{1}{2}\)sec
Speed of the train \( \frac{x+50}{\frac{9}{2}}\)m/s
Again, the time taken by the train to cover x metres in 2 seconds.
Speed of the train = \( \frac{x}{2}\)metre per second ..(ii)
From equations (i) and (ii), we have
\( \frac{}{}\)=\( \frac{x}{2}\)
4x + 200 = 9x
5x = 200
x = 40
Length of the train
= 40 metre
Speed of the train=\( \frac{40}{2}\)=20 m/sec

Q.44

Two places A and B are 162 kms apart. A train leaves A for B and at the same time another train leaves B for A. The two trains meet at the end of 6 hours. If the train travelling from A to B travels 8 km per hr. faster than the other, find the speed of the faster train.

(1) 16.5 kmph

(2) 16 kmph

(3) 17 kmph

(4) 17.5 kmph

Ans .

(4) 17.5 kmph

Explanation :

Bo th trains meet after 6 hours.
The relative speed of two trains =\( \frac{162}{6}\)== 27 km per hr..
The speed of the slower train starting from B =\( \frac{19}{2}\) km per hr..
The speed of the faster train =w\( \frac{35}{2}\)= 17.5 km per hr..

Q.45

A train running at 25 km per hour take 18 seconds to pass a plat- form. Next, it takes 12 seconds to pass a man walking at the rate of 5 km per hr. in the same di- rection. Find the length of the platform.

(1) 25 metres

(2) 20 metres

(3) 24 metres

(4) 28 metres

Ans .

(1) 25 metres

Explanation :

Let the length of train be x metres and the length of platform be y metres.
Speed of the train 25*\( \frac{5}{18}\)=\( \frac{125}{18}\)
Time taken by train to pass the platform
x+y *\( \frac{18}{125}\) or, x + y = 125 ...(i)
Speed of train relative to man = (25 + 5) km per hr.
30*\( \frac{5}{18}\)=\( \frac{25}{3}\)
Time taken by the train to pass the man
x*\( \frac{3}{25}\)
x=100 metres
length of the platform = 25 metres

Q.46

Two trains 200 metres and 175 metres long are running on parallel lines.They take 7\( \frac{1}{2}\)when running in opposite direction and 37\( \frac{1}{2}\)seconds when running in the same direction to pass each other. Find their speeds in km per hour.

(1) 118 kmph ; 75 kmph

(2) 108 kmph ; 72 kmph

(3) 120 kmph ; 75 kmph

(4) 125 kmph ; 80 kmph

Ans .

(2) 108 kmph ; 72 kmph

Explanation :

Let the speed of the train be x metre per sec. and y metre per sec. respectively.
Sum of the length of the trains = 200 + 175 = 375 metres
Case : I
When the trains are moving in opposite directions Relative speed = (x + y) m per sec.
In this case the time taken by the trains to cross each other =\( \frac{375}{x+y}\)
\( \frac{375}{x+y}\)=\( \frac{15}{2}\)
x + y = 50
Case : II
When the trains are moving in the same direction.
Relative speed = (x – y) m per sec.
In this case, the time taken by the trains to cross each other \( \frac{375}{x-y}\)=\( \frac{75}{2}\)
x – y = 10
Now, x + y = 50
x – y = 10
x=30
Putting this value in equation (i), we have
y = 50 – 30 = 20
\ Speed of trains = 30 m per sec.
=30*\( \frac{18}{5}\) = 108 km per hr.
and 20 m per sec. = 20 * \( \frac{18}{5}\)
= 72 km per hr.

Q.47

A train travelling at the rate of 60 km per hr, while inside a tun- nel, meets another train of half its length travelling at 90 km per hr. and passes completely in 4 \( \frac{1}{2}\) seconds. Find the length of the tunnel if the first train passes completely through it in 4 minutes 37\( \frac{1}{2}\) sec

(1) 5 km

(2) 3.5 km

(3) 4.5 km

(4) 6 km

Ans .

(3) 4.5 km.

Explanation :

Trains are running in oppo- site direction Relative speed of the two trains = 90 + 60 = 150 km per hr.
Distance travelled in 4\( \frac{1}{2}\)seconds onds with speed of 150 km per hr
=150*\( \frac{5}{18}\)=150*\( \frac{5}{18}\)*( \frac{9}{2}\)=\( \frac{375}{2}\)
Let the length of the first train be x metres.
Then the length of the second train be \( \frac{x}{2}\)
\( \frac{3x}{2}\)=\( \frac{375}{2}\)
3x = 375
x = 125 metres
Hence, the length of the first train = 125 metres
Speed of the first train = 60 km per hr.
60*\( \frac{5}{18}\)=\( \frac{50}{3}\)
Time taken by the first train to cross the tunnel = 4 minutes and 37\( \frac{1}{2}\)sec
240+\( \frac{75}{2}\)sec=\( \frac{555}{2}\)sec
Speed of first train =\( \frac{50}{3}\)
Distance covered by it in \( \frac{555}{2}\) sec
=\( \frac{50}{3}\)*\( \frac{555}{2}\)
= 4625 metres
Hence, length of tunnel = 4625 – 125 = 4500 metres
= 4.5 km

Q.48

A train overtakes two person walking at 2 km per hr. and 4 km per hr. respectively and passes completely them in 9 sec. and 10 sec. respectively. What is the length of the train?

(1) 65 metres

(2) 60 metres

((3) 55 metres

(4) 50 metres

Ans .

(4) 50 metres

Explanation :

Let the length of the train be x km and its speed y km per hr.
Case I : When it passes the man walking at 2 km per hr. in the same direction
Relative speed of train = (y – 2) km per hr.
\( \frac{x}{y-2}\)=9 sec
=\( \frac{1}{400}\)hr
Case II : When the train crosses the man walking at 4 km per hr. in the same direction.
Relative speed of train= (y – 4) km per hr.
\( \frac{x}{y-4}\)=10 sec
\( \frac{x}{y-4}\)=\( \frac{1}{360}\)hr
On dividing equation (i) by (ii), we have
\( \frac{y-4}{y-2}\)=\( \frac{\frac{1}{400}}{\frac{1}{360}}\) =\( \frac{360}{400}\) =\( \frac{9}{10}\)
10y – 40 = 9y – 18
10y – 9y = 40 – 18
y = 22 km per hr.
\ From equaton (i), we have
\( \frac{x}{22-2}\)=\( \frac{1}{400}\)
x=50 metres

Q.49

A train takes 18 seconds to pass completely through a station 162 metres long and 15 seconds to pass completely through another station 120 metres long. Find the speed of train in km per hr.

(1) 50.4 kmph

(2) 52 kmph

(3) 55 kmph

(4) 60 kmph

Ans .

(1) 50.4 kmph

Explanation :

Let the length of the train be x metres
Then, in 18 sec. the train trav- els (x + 162) metres ...(i)
and in 15 sec. the train travels (x + 120) metres
In (18 – 15) = 3 sec. the train travels (x + 162) – (x + 120) = 42m.
In 1 sec the train travels =14 metres
In 18 sec. the train travels
= 14 × 18 = 252 metres ...(iii)
From equations (i) and (iii)
\ x + 162 = 252
Þ x = 252 – 162 = 90
\ Length of the train = 90 metres
Also, from equation (ii) we see that in 1hr. the train travels = 14 × 60 × 60 metres
\( \frac{14*60*60}{1000}\)=50.4
The speed of the train = 50.4 km per hr.

Q.50

Two trains of which one is 50 metres longer than the other are running in opposite directions and cross each other in 10 sec- onds. If they be running in the same direction then faster train would have passed the other train in 1 minute 30 seconds. The speed of faster train is 90 km per hr. Find the speed of other train.

(1) 25 m/sec.

(2) 20 m/sec.

(3) 30 m/sec.

(4) 35 m/sec.

Ans .

(2) 20 m/sec.

Explanation :

Let the length of trains be x m and (x + 50)m and the speed of other train be y m per sec.
The speed of the first train = 90 km per hr.
90*\( \frac{5}{18}\)= 25 m per sec.
Case I : Opposite direction, Their relative speed = (y + 25)m per sec.
Distance covered = x + x + 50
= 2x + 50 metres
Time taken= \( \frac{2 x + 50}{y + 25}\)=10
2x + 50 = 10y + 250 ...(i)
Case II. Direction is Same Their relative speed = (25 – y) m per sec.
Distance covered = x + x + 50
= 2x + 50m
Time taken= \( \frac{2 x + 50}{25-y}\)=90
2x + 50 = 90 (25 – y)
From equations (i) and (ii)
10y + 250 = 2250 – 90y
10y + 90y = 2250 – 250
y=20
Putting y = 20 in equation (i), we have 2x + 50= 10 × 20 + 250 = 450
x=200
x + 50 = 200 + 50
= 250 metres.
Hence, The length of the 1st train = 200 metres.
The length of the 2nd train = 250 metres.
The speed of the 2nd train = 20 m per sec

Q.51

A man standing on a 170 metre long platform watches that a train takes 7\( \frac{1}{2}\)sec to pass him and 21 seconds to cross the plat- form. Find the speed of train.

(1) 12.59 m/sec

(2) 13.59m/sec

(3)13 m/sec

(4)12.50 m/sec

Ans .

(1)12.59 m/sec.

Explanation :

Let the length of the train be x m and its speed y m/sec. Distance covered in crossing the platform = 170 + x metres
and time taken = 21 seconds Speed y= \( \frac{170+x}{21}\)
Distance covered to cross the man = x metres and time taken = \( \frac{15}{2}\)sec
Speed y=\( \frac{2x}{15}\)
From equations (i) and (ii),
\( \frac{170+x}{21}\)=\( \frac{2x}{15}\)
2550 + 15x = 42x
Þ 42x – 15x = 2550
Þ 27x = 2550
x=94.44m/sec
and y=\( \frac{340}{27}\)
y=12.59m/sec

Q.52

A goods train 158 metres long and travelling at the speed of 32 km per hr. leaves Delhi at 6 am. Another mail train 130 metres long and travelling at the aver- age speed of 80 km per hr. leaves Delhi at 12 noon and follows the goods train. At what time will the mail train completely cross the goods train?

(1) 4 hours

(2) 4 hours 21.6 sec.

(3) 5 hours 21.6 sec.

(4) None of these

Ans .

(2) 4 hours 21.6 sec..

Explanation :

The goods train leaves Delhi at 6 am and mail train at 12 noon, hence after 6 hours
The distance covered by the goods train in 6 hours at 32 km per hr. = 32 * 6 = 192 kms
The relative velocity of mail train with respect to goods train = 80 – 32 = 48 km per hr.
To completely cross the goods train, the mail train will have to cover a distance
= 192 km + 158m + 130m
= 192km + 0.158 km + 0.130 km
= 192.288 km more
Since, the mail train goes 48 kms more in 1 hour.
\ The mail train goes 192.288 kms more in \( \frac{192288}{1000}\)*\( \frac{1}{48}\)=\( \frac{2003}{500}\) = 4 hours 21.6 sec.

Q.53

A motor-boat goes 2 km up- stream in a stream flowing at 3 km per hr. and then returns downstream to the starting point in 30 minutes. Find the speed of the motor-boat in still water.

(1) 9.5 kmph

(2) 8.5 kmph

(3) 9 kmph

(4) 8 kmph

Ans .

(3) 9 kmph .

Explanation :

Let the speed of the motor- boat in still water be Z km per hr.
Downstream speed= (Z + 3) km per hr. Upstream speed = (Z – 3) km per hr.
Total journey time
= 30 minutes =\( \frac{1}{2}\)hr
We can write,
\( \frac{2}{z-3}\)+\( \frac{2}{z+3}\)=\( \frac{1}{2}\)
Z ²– 9 = 8Z
Z ² – 8Z – 9 = 0
Z² + Z – 9Z – 9 = 0
Z(Z + 1) – 9 (Z + 1) = 0
(Z + 1) (Z – 9) = 0
Z = – 1 or 9.
Since speed can’t be negative Therefore, the speed of the mo- tor-boat in still water = 9 km per hr.

Q.54

A person can row a boat 32 km upstream and 60 km down- stream in 9 hours. Also, he can row 40 km upstream and 84 km downstream in 12 hours. Find the rate of the current.

(1) 3 kmph

(2) 2.5 kmph

(3) 1.5 kmph

(4) 2 kmph

Ans .

(4) 2 kmph

Explanation :

Let the upstream speed be x km per hr. and downstream speed be y km per hr.
Then, we can write,
\( \frac{32}{x}\)+\( \frac{60}{y}\)=9and
\( \frac{40}{x}\)+\( \frac{84}{y}\)=12
Let \( \frac{1}{x}\)=m and \( \frac{1}{y}\)=n
The above two equations can now be written as
32 m + 60 n = 9 ...(i)
and, 40 m + 84 n = 12 ...(ii)
7 × (i) – 5 × (ii) gives 24 m = 3
or x=8 4 × (ii) – 5 × (i) gives 36 n = 3
y=12km per hr..
Rate of current \( \frac{y-x}{2}\)
= 2 km. per hr..

Q.55

A boatman takes his boat in a river against the stream from a place A to a place B where AB is 21 km and again returns to A. Thus he takes 10 hours in all. The time taken by him down- stream in going 7 km is equal to the time taken by him against stream in going 3 km. Find the speed of river.

(1) 2 kmph

(2) 2.5 kmph

(3) 3 kmph

(4) 3.5 kmph

Ans .

(1) 2 kmph

Explanation :

Let the speed of boat and riv- er be x km per hr. and y km per hr. respectively. Then,
The speed of boatman down- stream = (x + y) km per hr.
and the speed of boatman up- stream = (x – y) km per hr.
Time taken by boatman in going 21 km downstream=\( \frac{21}{x+y}\)hours
Time taken by boatman in going 21 km upstream =\( \frac{21}{x-y}\)hours
According to the question,
\( \frac{21}{x+y}\)+\( \frac{21}{x-y}\)=10
Now, time taken for 7 kms downstream =\( \frac{7}{x+y}\)
and time taken for 3 kms upstream =\( \frac{3}{x-y}\)
\( \frac{7}{x+y}\)-\( \frac{3}{x-y}\)=0
Therefore,x + y = 7 and x – y = 3 On adding (iii) and (iv), we have
2x = 10
Þ x = 5
\ y = 7 – x = 7 – 5 = 2
\ Speed of river = 2 km per hr.

Q.56

A motorist and a cyclist start from A to B at the same time. AB is 18 km. The speed of mo- torist is 15 m per hr. more than the cyclist. After covering half the distance, the motorist rests for 30 minutes and thereafter his speed is reduced by 20%. If the motorist reaches the destination B, 15 minutes earlier than that of the cyclist, then find the speed of the cyclist.

(1) 16 kmph

(2) 12 kmph

(3) 14 kmph

(4) 15 kmph

Ans .

(2) 12 kmph

Explanation :

Let the speed of the cyclist be x km per hr.
Speed of the motorist= (x + 15) km per hr.
Time taken by the motorist to cover half of the distance=\( \frac{9}{x+15}\)hr
After covering 9 kms, the speed of motorist gets reduced by 20%
New speed = x + 15*\( \frac{80}{100}\)=\( \frac{4(x+15)}{5}\)
Time taken by the motorist to cover the remaining half distance=\( \frac{45}{4(x+15)}\)
Total time taken by the motorist=\( \frac{9}{x+15}\)+\( \frac{1}{2}\)+\( \frac{45}{4*x+15}\)
Total time taken by the cyclist=\( \frac{18}{x}\)
Motorist reaches 15 minutes, i.e.,\( \frac{1}{4}\)
\( \frac{18}{x}\)-\( \frac{9}{x+15}\)-\( \frac{1}{2}\)-\( \frac{45}{4*x+15}\)=\( \frac{1}{4}\)
72x + 1080 – 36x – 2x 2 –
30x – 45x = x 2 + 15x
Þ 3x 2 + 54x – 1080 = 0
Þ x 2 + 18x – 360 = 0
Þ x 2 + 30x – 12x – 360 = 0
Þ x (x + 30) – 12 (x + 30) = 0
Þ (x + 30) (x – 12) = 0
Þ x = – 30, 12
The speed cannot be negative.
\ The speed of the cyclist = 12 km per hr.

Q.57

A man covered a distance of 3990 km partly by air, partly by sea and remaining by land. The time spent in air, on sea and on land is in the ratio 1 : 16 : 2 and the ratio of average speed is 20 : 1 : 3 respectively. If total av- erage speed is 42 km per hr, find the distance covered by sea.

(1) 1720 km.

(2) 1620 km.

(3) 1520 km.

(4) 1820 km.

Ans .

(3) 1520 km.

Explanation :

Total distance travelled = 3990 km
Distance = Time × Speed
Ratio of time spent = 1 : 16 : 2
Ratio of speed = 20 : 1 : 3
Ratio of time × speed
= 20 × 1 : 16 × 1 : 2 × 3
= 20 : 16 : 6
Sum of the ratios
= 20 + 16 + 6 = 42
Distance covered by sea=\( \frac{3990}{42}\)*16=1520 kms

Q.58

A railway engine is proceeding towards A at uniform speed of 30 km/hr. While the engine is 20 kms away from A an insect starting from A flies again and again between A and the engine relentlessly. The speed of insect is 42 km per hr. Find the dis- tance covered by the insect till the engine reaches A.

(1) 25 km.

(2) 32 km.

(3) 30 km.

(4) 28 km.

Ans .

(4) 28 km.

Explanation :

Relative speed of insect = 30 + 42 = 72 km per hr.
Distance between railway engine and insect = 20 km.
Engine and insect will meet for the first time after =\( \frac{20}{72}\)hr.
Distance covered in this period \( \frac{20}{72}\)* 42 =\( \frac{35}{3}\) km returning to A.
The distance covered by engine in this period=\( \frac{20}{72}\)* 30 =\( \frac{25}{3}\)
Remaining distance between
A and engine 20- \( \frac{25}{3}\)+\( \frac{25}{3}\)=\( \frac{10}{3}\)
Again, engine and insect will meet after =\( \frac{5}{108}\)hr
The distance covered by the in- sect in this period \( \frac{5}{108}\)*42 =\( \frac{35}{18}\)
and again the insect will cover \( \frac{35}{18}\) km in returning.
Total distance covered by the insect =\( \frac{70}{3}\)+\( \frac{70}{18}\) +....
[\( \frac{35}{3}\)+\frac{35}{3}\)=\frac{70}{3}\)and \frac{35}{18}\)+\frac{35}{18}\)=\frac{70}{18}\)....]
=\( \frac{70}{3}\)[1+\( \frac{1}{6}\)........]
It is a Geometric Progression to infinity with common ratio \( \frac{1}{6}\)
=\( \frac{70}{3}\) *\( \frac{1}{\frac{5}{6}}\)=28 km

Q.59

Distance between two stations X and Y is 220 km. Trains P and Q leave station X at 8 a.m. and 9.51 a.m. respectively at the speed of 25 kmph and 20 kmph respec- tively for journey towards Y. A train R leaves station Y at 11.30 a.m. at a speed of a 30 kmph. for journey towards X. When will P be at equal distance from Q and R ?

(1) 12:48 pm.

(2) 12:30 pm.

(3) 12:45 pm.

(4) 11:48 pm.

Ans .

(1) 12:48 pm..

Explanation :

Let P be at equal distance from Q and R after t hours.
(87.5 – 33) + 5t
t= 1 hr 18 minutes
11.30 am + 1 hr. 18 min. = 12.48 pm
At 12.48 pm, P would have cov- ered a distance
= (12.48 pm – 8 am) × 25
= 120 km
Therefore, P will be at equal dis- tance from Q and R at 12.48 pm

Q.60

A person travels a certain dis- tance on a bicycle at a certain speed. Had he moved 3 km/hour faster, he would have taken 40 minutes less. Had he moved 2km/hour slower, he would have taken 40 minutes more. Find the distance.

(1) 45 km.

(2) 40 km.

(3) 50 km.

(4) 55 km.

Ans .

(2) 40 km.

Explanation :

Let the original speed of the person be x km/hr. and the dis- tance be y km.
Case 1:
\( \frac{y}{x}\)-\( \frac{y}{x+3}\)=40 minutes
or \( \frac{3y}{x(x+3)}\)=\( \frac{2}{3}\)
or, 2 x (x + 3) = 9y...(i)
Case II :
\( \frac{2y}{x(x-2)}\)=\( \frac{2}{3}\) or, x (x – 2) = 3y... (ii)
On dividing equation (i) by (ii) we have,
\( \frac{2(x+3)}{x-2}\)=\( \frac{2}{3}\) or, x = 12 km/hr.
Original speed of the person = 12 km/hr.
Putting the value of x in equa- tion (ii)
12 (12 – 2) = 3y
or, 3y = 12 × 10
y=40
The required distance =40 km

Q.61

A steamer goes downstream from one port to another in 4 hours. It covers the same distance up- stream in 5 hours. If the speed of the stream be 2 km/hr, find the distance between the two ports.

(1) 60 km.

(2) 45 km.

(3) 80 km.

(4) 65 km.

Ans .

(3) 80 km.

Explanation :

Let the speed of steamer in still water = x kmph \ Rate downstream = (x + 2) kmph
Rate upstream = (x – 2) kmph Obviously, distance covered downstream and upstream are equal
Þ 4 (x + 2) = 5 (x – 2)
4x + 8 = 5x – 10
Þ 5x – 4x = 10 + 8 Þ x = 18
\ Rate downstream
= 18 + 2 = 20 kmph
Therefore, the required distance
= Speed downstream × Time
= 20 × 4 = 80 km.

Q.62

In a 200 metre race, A beats B by 20 metres; while in a 100 metres race, B beats C by 5 metres. Assuming that the speed of A, B and C remain the same in various races, by how many metres will A beat C in one kilometre race ?

(1) 140 metre

(2) 145 metre

(3) 135 metre

(4) 125 metre

Ans .

(2) 145 metre.

Explanation :

According to the question, when A covers the distance of 200 metres, B covers only 200– 20 = 180 metres
Again, in 100 metre race, B beats C by 5 metres.
Hence, if B runs 100 metres, C runs 100–5 = 95 metres Q If B runs 100 m, C runs = 95 m
If B runs 180 m, C runs \( \frac{95*180}{100}\)= 171 m
A : B : C = 200 : 180 : 171
Hence, A will beat C by = 200–171 = 29 m in 200 m race.
i.e., 29 × 5 = 145 m in 1 km race.

Q.63

Two places A and B are 80 km apart from each other on a highway. A car starts from A and another from B at the same time. If they move in the same direction, they meet each other in 8 hours. If they move in opposite directions towards each other, they meet in 1 hour 20 minutes. Determine the speed of the faster car.

(1) 20 kmph

(2) 25 kmph

(3) 35 kmph

(4) 30 kmph

Ans .

(3) 35 kmph

Explanation :

Case I : When the cars are moving in the same direction.
Let A and B be two places and C be the place of meeting.
Let the speed of car starting from A be x kmph, and that of car starting from B be y kmph.
Relative speed = (x – y) kmph
According to the question.
(x – y) × 8 = 80
x – y = 10
Case II : When the cars are mov- ing in the opposite directions and they meet at point C.
Relative speed = (x + y) kmph
Time taken = 1 hour 20 minutes
1+\( \frac{1}{3}\)=\( \frac{4}{3}\) hr
x+y *\( \frac{4}{3}\)=80
x + y = 60
Adding equations (i) and (ii),
2x = 70
x = 35 Þ From equation (ii),
x + y = 60
35 + y = 60
Þ y = 60 – 35 = 25
\ Speed of the faster car = 35 kmph

Q.64

In a one-kilometre race, A beats B by 15 seconds and B beats C by 15 seconds. If C is 1 00 metres away from the finishing mark, when B has reached it, find the speed of A.

(1) 9.5 m/sec.

(2) 9 m/sec.

(3) 8 m/sec.

(4) 8.3 m/sec.

Ans .

(4) 8.3 m/sec.

Explanation :

Let B take x seconds to run 1000 m.
\ Time taken by C
= (x + 15) seconds
\( \frac{x}{x+15}\)=\( \frac{9}{10}\)
10x = 9x + 135
Þ x = 135 seconds
Now in a one kilometre race, A beats B by 15 seconds.
It means A covers 1000 m in 135 – 15 = 120 seconds
Speed of A =\( \frac{1000}{120}\)=8.3 m/sec.

Q.65

A train running at the speed of 72 km/hr passes a tunnel com- pletely in 3 minutes. While in- side the tunnel, it meets another train of \( \frac{3}{4}\)of its length coming from opposite direction at the speed of 90km/hr and passes it completely in 3\( \frac{1}{2}\)seconds. Find the length of the tunnel.

(1) 3510 metre

(2) 3500 metre

(3) 3400 metre

(4) 3600 metre

Ans .

(1) 3510 metre.

Explanation :

Trains are running in oppo- site directions.
Relative speed = 72 + 90 = 162 kmph
=162*\( \frac{5}{18}\)=45
Let the length of the first train be = x metre.
\ Length of the second train \( \frac{3}{4}\)x distance travelled in 3 \( \frac{1}{2}\)onds at 45 m/sec =\( \frac{315}{2}\)
This distance is equal to sum of the lengths of trains.
x+\( \frac{3x}{4}\)=\( \frac{315}{2}\)
x=90
Hence, the length of the first train = 90 metre.
Speed of first train = 72 kmph
72* \( \frac{5}{18}\)= 20 m/sec
Time taken by the first train to cross the tunnel
= 3 minutes = 180 seconds
\ Distance covered by it in 180 seconds
= 180 × 20 = 3600 metre
\ Length of (first train + tunnel) = 3600 metre
\ Length of tunnel = 3600 – 90 = 3510 metre

upscfever.com

TIME AND DISTANCE

TYPE-I

TYPE-2

TYPE-3

TYPE-4

TYPE-5

TYPE-6

TYPE-7

TYPE-8

TYPE-9

TYPE-10

TYPE-11

TYPE-12

TEST YOURSELF

UPSCFEVER - POPULAR PAGES

Join The Movement

Discussions and Comments